Math ML - Modified Softmax w/ Margin
[@rashadAdditiveMargin2020] and [@liuLargeMarginSoftmax2017] Softmax classification 是陳年技術,可還是有人在老幹上長出新枝。其中一類是在 softmax 加上 maximum margin 概念 (sometimes refers to metric learning), 另一類是在 softmax 所有 dataset 中找出 “supporting vectors” 減少 computation 卻不失準確率。實際做法都是從修改 loss function 著手。本文聚焦在第一類增加 margin 的 算法。
Softmax in DL or ML Recap
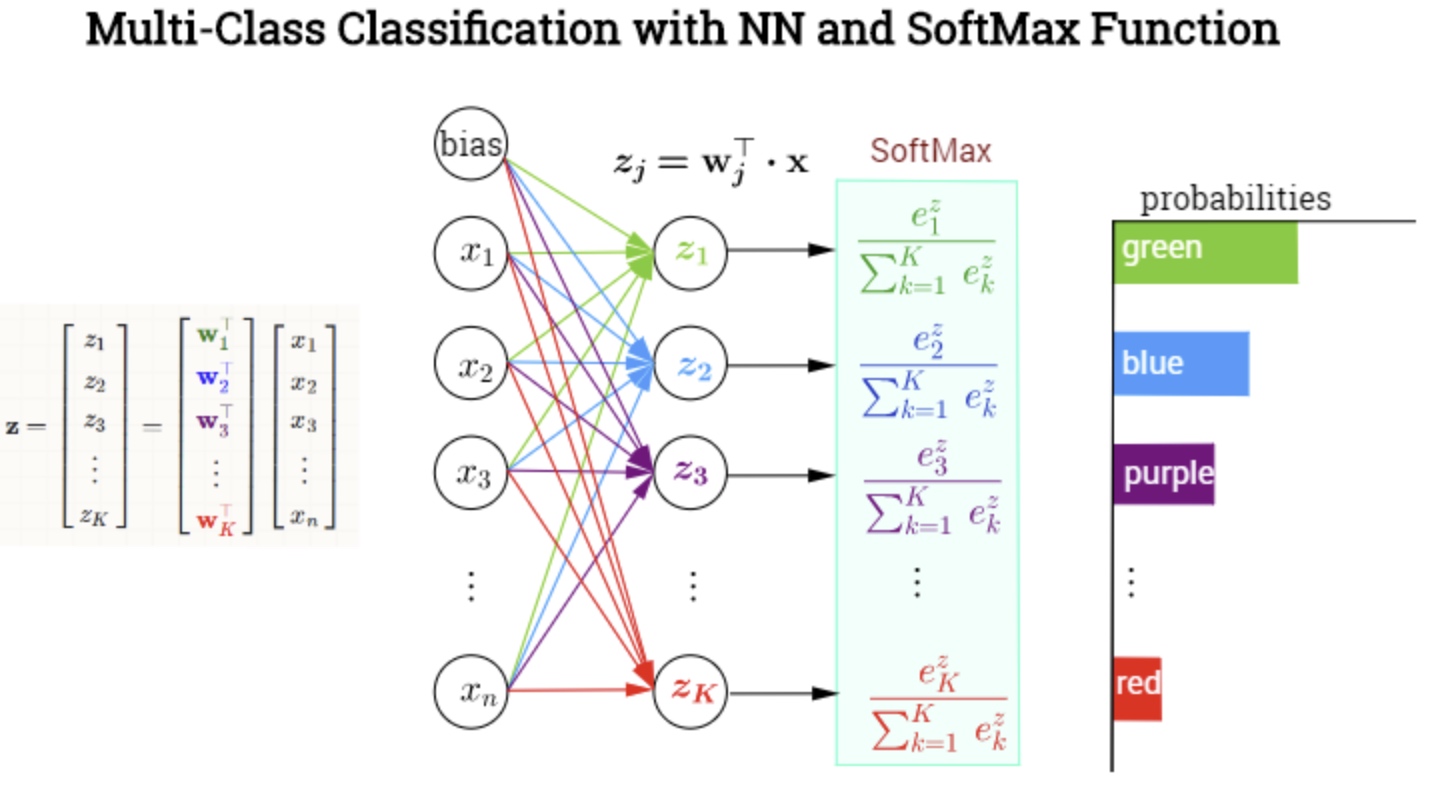
Softmax 最常用於 DL (i.e. deep layers) 神經網絡最後一層(幾層)的 multi-class classification 如下圖。 \(\sigma(j)=\frac{\exp \left(\mathbf{w}_{j}^{\top} \mathbf{x}\right)}{\sum_{k=1}^{K} \exp \left(\mathbf{w}_{k}^{\top} \mathbf{x}\right)}=\frac{\exp \left(z_{j}\right)}{\sum_{k=1}^{K} \exp \left(z_{k}\right)}\) and \(\frac{\partial}{\partial z_{i}} \sigma\left(z_{j}\right)=\sigma\left(z_{j}\right)\left(\delta_{i j}-\sigma\left(z_{i}\right)\right)\)
- Input vector, $\mathbf{x}$, dimension $n\times 1$.
- Weight matrix, $\mathbf[w_1’, w_2’, .., w_K’]’$, dimension $K\times n$
- Output vector, $\mathbf{z}$, dimension $K\times 1$.
- Softmax output vector, $0\le\sigma(j)\le 1, j=[1:K]$, dimension $K\times 1$.
- 注意 bias 如果是一個 fixed number, $b$, softmax 分子分母會抵銷。bias 如果不同 $b_1, b_2, …, b_n$,可以擴展 $\mathbf{x’ = [x, }1]$ and $\mathbf{w’_j = [w_j}, b_j]$, 同樣如前適用。
Softmax 也常用於 ML (i.e. shallow layers) 的 multi-class classification, 常和 SVM 一起比較。為了處理 nonlinear dataset or decision boundary, Softmax + kernel method 是一個選項。
Softmax 另外用於 attention network, TBD.
Parameter Notation and Range for ML and DL
- $N$: number of data points. 100 to 10,000 for ML, > 1M for DL.
- $n$: input vector dimension. maybe from 1~ to 100~ for ML, 1000-4000 for DL.
- $K$ or $m$ or $C$: output vector dimension, number of classes, maybe from 1 (binary) to 100 (Imaginet)
- $k$: kernel feature space dimension, maybe from 10s’ - $\infty$ for ML. Usually not use for DL.
Summarize the result in table.
| N | n | k | K | |
|---|---|---|---|---|
| ML | 100-10,000 | 1s’- 100s’ | 10s’- $\infty$ | 1s’-10s’ |
| DL | > 1M | 1000-4000 | NA | 10-100 |
Softmax w/ Margin Via Training
根據前文討論,$w_i$ vectors 代表和 class i data 的相似性。
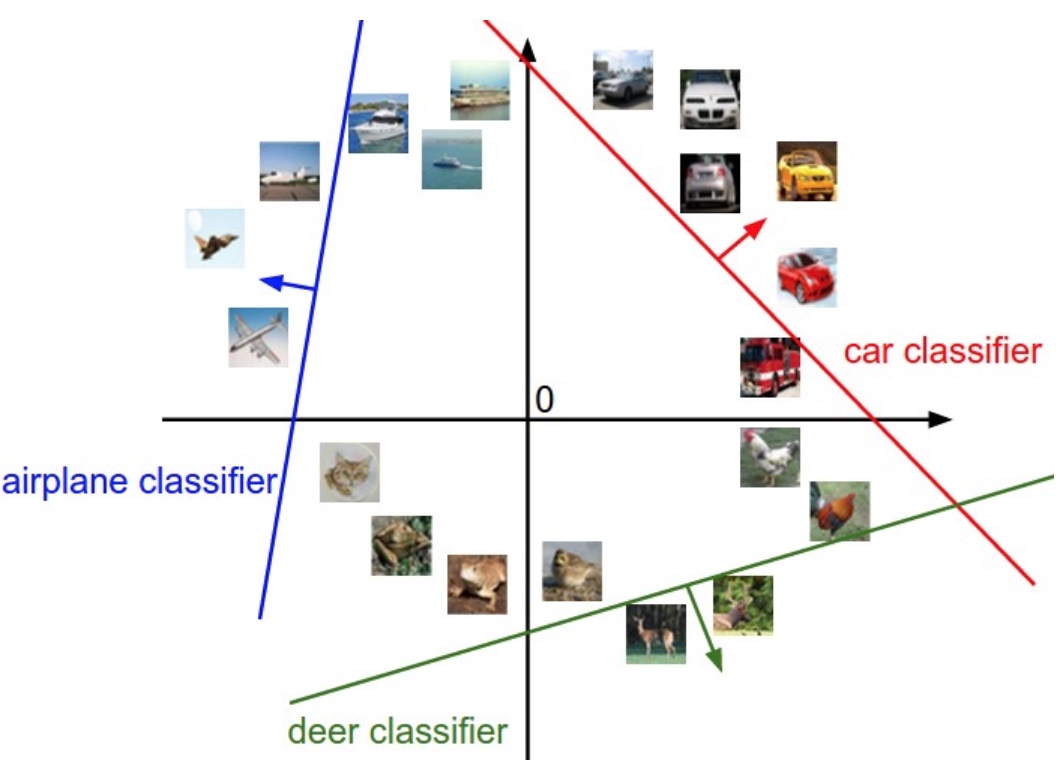
普通的 softmax classification 如下圖左所示。
Decision boundary 是 data point 和 $w_1$ and $w_2$ 的機率一樣。 因為 softmax (or logistic regression) 只要求 $\sigma_1(x) > \sigma_2(x)$ or vice versa to classify $x \in$ class 1 (or class 2). 這裡完全沒有 margin 的觀念。

推廣到 multiple class 更是如此,如下圖。因為是取 $\sigma(j)$ 的最大值。除了 $\sigma(j) > 0.5$ 有明顯的歸類。但在三不管地帶,很可能雜錯在一起。
因爲 training 是基於 loss function, 解法是在 loss function 加入 margin term 做為 driving force (check the back-prop gradient!), 讓 training process 竭盡所能 “擠出” margin, 如上圖右。
如何在 softmax 加入 margin for training
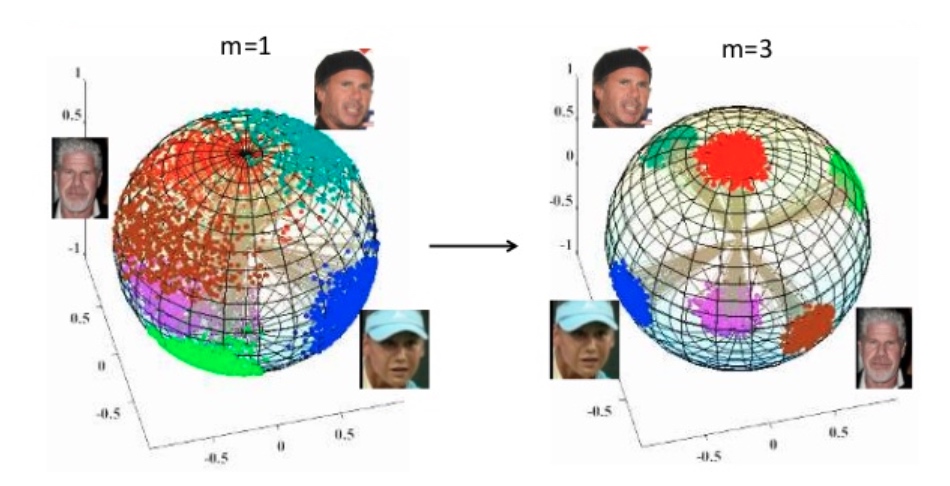
SVM 是從 decision boundary 的平行線距離著手(margin = 1/|w|, minimize |w| ~ maximum margin)。 本文討論 Softmax 加上 margin 有三種方式,都是從角度 $\theta$ 著手,概念如圖二右 (平面角度),或是下圖右 (球面角度)。maximize $\theta$ 剛好和 minimize |w| 正交 (orthogonal). 這是巧合嗎?
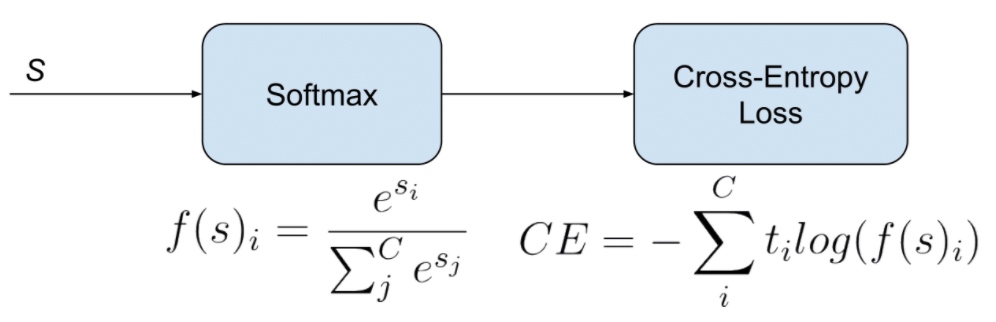
我們先看 Softmax 的 loss function 如下圖。先是 softmax function, inference/test 只要 再來通過 cross-entropy loss. Cross-entropy loss 對應 log likelihood. \(L=\frac{1}{N} \sum_{i} L_{i}=\frac{1}{N} \sum_{i}-\log \left(\frac{e^{f_{y_{i}}}}{\sum_{j} e^{f_{j}}}\right)\)
where $f_{y_{i}}=\boldsymbol{W}{y{i}}^{T} \boldsymbol{x}{i}$ 代表 data $x_i$ 和 $W{y_i}$ 的相似性。
三種用角度增加 SoftMax inter-class margin
- L-Softmax (Large Margin Softmax) [@liuLargeMarginSoftmax2017]
- A-Softmax (Angular Softmax) [@liuSphereFaceDeep2018]
- AM-Softmax (Additive Margin Softmax)
L-Softmax (Large Margin Softmax): $\cos \theta \to \cos (m\theta)$
因為 $f_{j}=\left| \boldsymbol{W_j} \right|\left| \boldsymbol{x_i} \right|\cos\left(\theta_{j}\right)$. 如何在 $x_i$ 和 $W_j$ 加上 margin? 一個方法就是把 $\cos \theta$ 改成 $\cos m\theta$, why?
從相似性來看,$\cos(m\theta)$ 在同樣的角度”相似性”掉的比較快。因此在 training 時會強迫把同一 feature 的 data 擠壓在一起, reduce the intra-class distance. 達到增加 inter-class margin 的目的。
另外可以從 decision boundary 理解。Softmax 的 decision boundary,
$x\in$ Class 1: $\left|\boldsymbol{W_1}\right||\boldsymbol{x}| \cos \left( \theta_{1}\right)>\left|\boldsymbol{W_2}\right||\boldsymbol{x}| \cos \left(\theta_{2}\right)$
$x\in$ Class 2: $\left|\boldsymbol{W_1}\right||\boldsymbol{x}| \cos \left( \theta_{1}\right) < \left|\boldsymbol{W_2}\right||\boldsymbol{x}| \cos \left(\theta_{2}\right)$
and $\theta_1 + \theta_2 = \theta$ which is the angle between $W_1$ and $W_2$
如果把 $\cos \theta \to \cos (m\theta)$,
$x\in$ Class 1: $\left|\boldsymbol{W_1}\right||\boldsymbol{x}| \cos \left( m\theta_{1}\right)>\left|\boldsymbol{W_2}\right||\boldsymbol{x}| \cos \left(\theta_{2}\right)$.
Assuming $|W_1| = |W_2| \to \theta_1 < \theta_2/m$, 因為 $\cos\theta$ 是遞減函數。
$x\in$ Class 2: $\left|\boldsymbol{W_1}\right||\boldsymbol{x}| \cos \left( \theta_{1}\right) < \left|\boldsymbol{W_2}\right||\boldsymbol{x}| \cos \left(m\theta_{2}\right)$.
Assuming $|W_1| = |W_2| \to \theta_1/m > \theta_2$.
此時我們有兩個 decision boundaries, 兩個 boundaries 之間可以視為 decision margin, 如下圖。
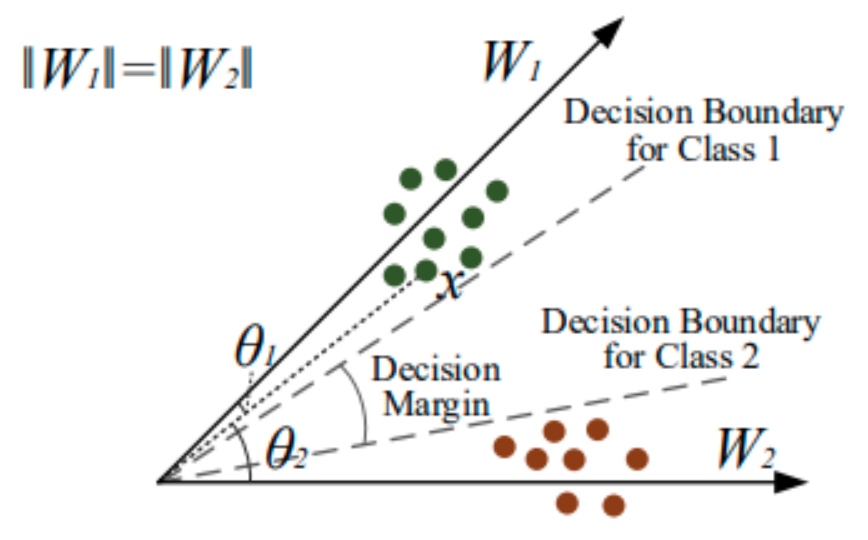
In summary, 就是在 labelled $c$ class 的 data 時,就把對應的 $\cos\theta_c$ 改成 $\cos (m\theta_c)$. $m$ 愈大,margin 就愈大。但過之猶如不及,如果 $m$ 太大,可能無法正確 capture features (TBC)? $m$ 應該有一個 optimal value.
\[L_{i}=-\log \left(\frac{e^{\left\|\boldsymbol{W}_{y_{i}}\right\|\left\|\boldsymbol{x}_{i}\right\| \psi\left(\theta_{y_{i}}\right)}}{e^{\left\|\boldsymbol{W}_{y_{i}}\right\|\left\|\boldsymbol{x}_{i}\right\| \psi\left(\theta_{y_{i}}\right)}+\sum_{j \neq y_{i}} e^{\left\|\boldsymbol{W}_{j}\right\|\left\|\boldsymbol{x}_{i}\right\| \cos \left(\theta_{j}\right)}}\right)\] \[\psi(\theta)=\left\{\begin{array}{l} \cos (m \theta), \quad 0 \leq \theta \leq \frac{\pi}{m} \\ \mathcal{D}(\theta), \quad \frac{\pi}{m}<\theta \leq \pi \end{array}\right.\]為什麼會有 $D(\theta)$? 原因是要維持 $\psi(\theta)$ 的遞減性,連續性,和可微分性 over $[0, \pi]$. 一旦定義出 $\psi(\theta)$ over $[0, \pi]$. 左右 flip (y 軸對稱) 得到 $\theta\in[-\pi, 0]$. 其他的 $\theta$ 都可以移到 $[-\pi, \pi]$.
舉一個例子如下式,$\psi(\theta)$ 的 curve 如下圖。 \(\psi(\theta)=(-1)^{k} \cos (m \theta)-2 k, \quad \theta \in\left[\frac{k \pi}{m}, \frac{(k+1) \pi}{m}\right]\)
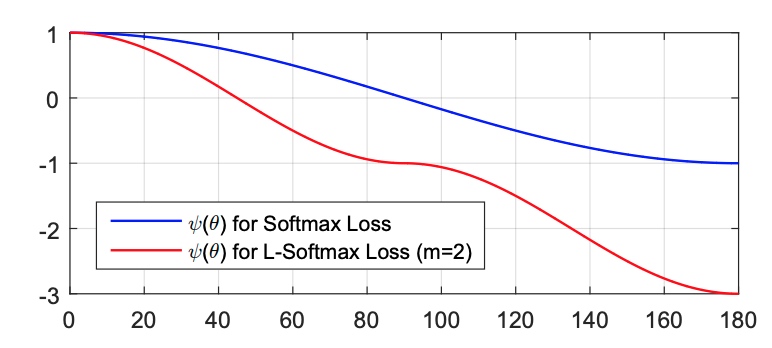
A-Softmax (Angular Softmax): $\cos \theta \to \cos (m\theta)$ and $|W|=1$
在 L-Softmax 可以同時調整 $|W|$ and $\theta$, 在 A-Softmax 進一步限制 $|W|=1$, 其他都和 L-Softmax 相同。A-Soft 的 Loss function 如下, \(L_{\mathrm{ang}}=\frac{1}{N} \sum_{i}-\log \left(\frac{e^{\left\|\boldsymbol{x}_{i}\right\| \cos \left(m \theta_{y_{i}, i}\right)}}{e^{\left\|\boldsymbol{x}_{i}\right\| \cos \left(m \theta_{y_{i}, i}\right)}+\sum_{j \neq y_{i}} e^{\left\|\boldsymbol{x}_{i}\right\| \cos \left(\theta_{j, i}\right)}}\right)\)
後來有再修正 $\psi(\theta)$, 多加一個 hyper-parameter $\lambda$, angle similarity curve 如下圖。注意 A-Softmax 的 $\psi(0)=1.$
\(\psi(\theta)=\frac{(-1)^{k} \cos (m \theta)-2 k+\lambda \cos (\theta)}{1+\lambda}\)
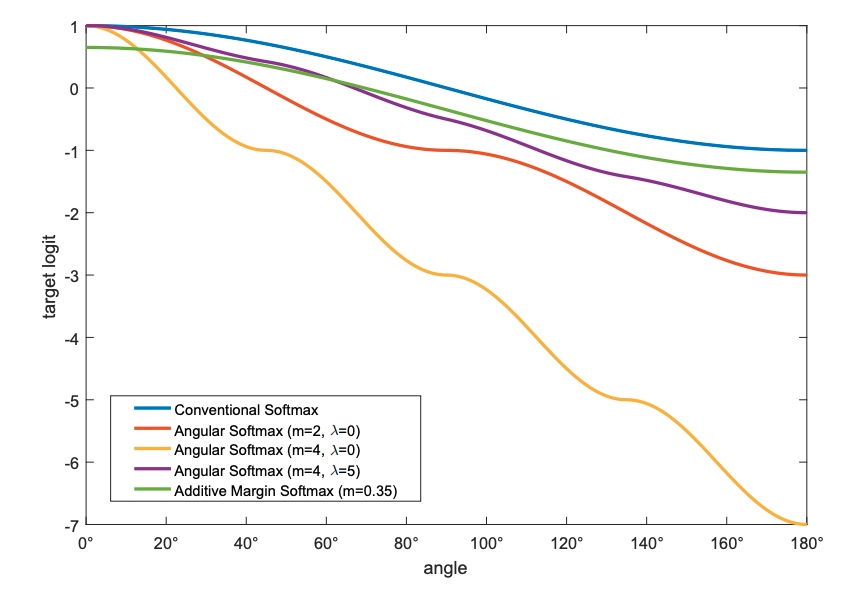
因為 $|W|=1$, A-Softmax 一個用途是 hyper-sphere explanation 如下圖。理論上 L-Softmax 包含 A-Softmax, 但在某一些情況下,A-Softmax 似乎效果更好,less is more? (同一作者,2017 L-SoftMax; 2018 A-Softmax).
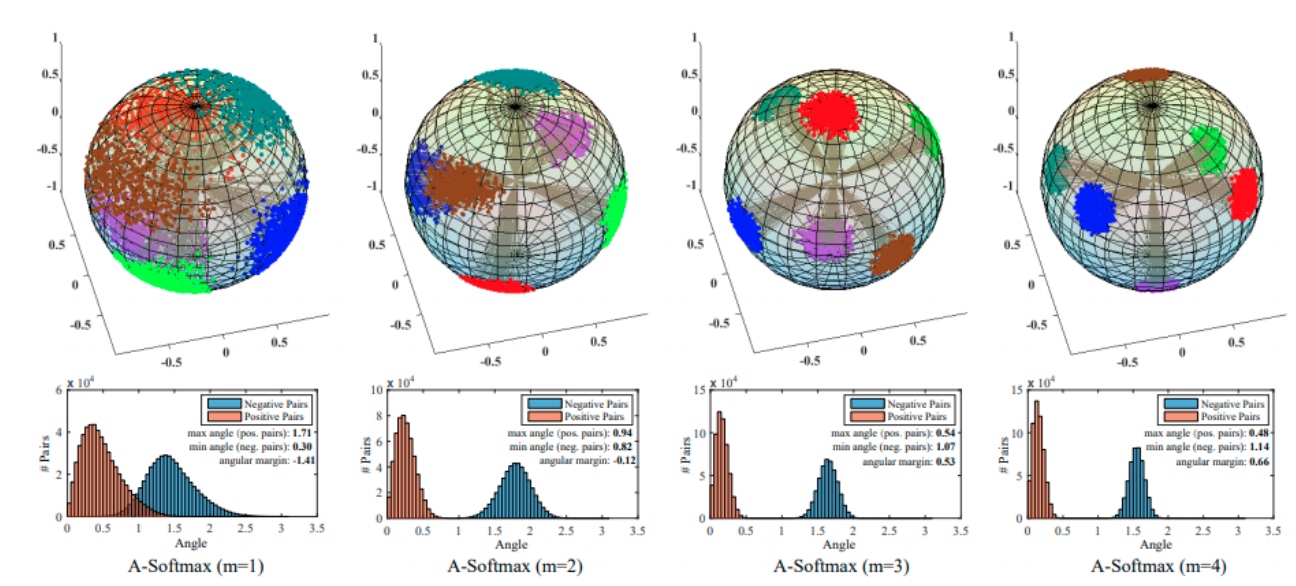
AM-Softmax (Additive Margin Softmax): $\cos \theta \to \cos \theta -m$
AM-Softmax 非常有趣,它把 $\cos\theta \to \cos(m\theta) \to \cos\theta -m$, 也就是, \(\psi(\theta)=\cos \theta-m\) AM-Softmax 的 loss function, 但多了一個 hyper-parameter $s$(?) \(\begin{aligned} \mathcal{L}_{A M S} &=-\frac{1}{n} \sum_{i=1}^{n} \log \frac{e^{s \cdot\left(\cos \theta_{y_{i}}-m\right)}}{e^{s \cdot\left(\cos \theta_{y_{i}}-m\right)}+\sum_{j=1, j \neq y_{i}}^{c} e^{s \cdot \cos \theta_{j}}} \\ &=-\frac{1}{n} \sum_{i=1}^{n} \log \frac{e^{s \cdot\left(W_{y_{i}}^{T} \boldsymbol{f}_{i}-m\right)}}{e^{s \cdot\left(W_{y_{i}}^{T} \boldsymbol{f}_{i}-m\right)}+\sum_{j=1, j \neq y_{i}}^{c} e^{s W_{j}^{T} \boldsymbol{f}_{i}}} . \end{aligned}\) 這有很多好處:
- 不用再分段算 $\psi(\theta)$, forward and backward 計算變成很容易。
- $m$ 是 continuous variable, 不是 discrete variable in A-Softmax. $m$ 可以 fine-grain optimized hyper-parameter. 而且是 differentiable, 我認為可以是 trainable variable.
- AM-Softmax 同時 push angle and magnitude?
Q&A
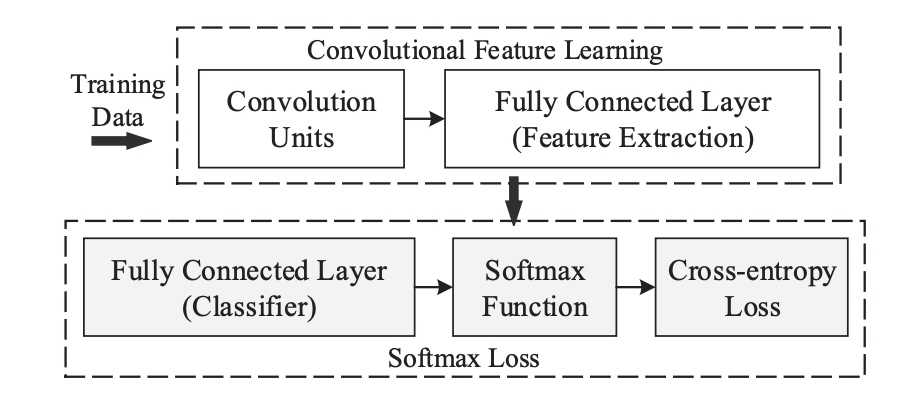
Q. Data 不是固定的嗎?為什麼會隨 loss function 改變? A. 此處是假設 CNN network 的最後一層是 Softmax, 因此 input data 對應的 feature extraction 並非固定而且會隨 loss function 改變如下圖。如果 input data 直接進入 Softmax with or without margin, the input data 顯然不會改變,但是 decision boundary may change? (next Q)
Q. 在 inference/test 時,以上的公式 (check class $c$) 加起來不等於 1? 如何解決? A: 以上的公式只用於 training 增加 margin? 在 inference/test 時,仍然用原來的 softmax 公式,因此機率仍然為 1.
Q. 以上 $cos(m \theta)$ 的 $m$ 一定要整數嗎? A. 整數可以定義 continuous and differentiable loss function in $0-\pi$ 角度。上上圖的角度顯示 $0-\pi/2$ 角度,$\pi/2 - \pi$ 是 $0-\pi/2$ 的左右 flip curve. 如果 $m$ 不是整數,在 $\pi/2$ is non-differentiable. 另外也讓 loss function 的分段比較麻煩。不過我認為這都不是什麼問題。重點是 $m$ 不是整數有沒有用? 我認為有用,可以視為另一個 hyper-parameter, or trainable parameter for optimization! $m$ 太小沒有 margin, $m$ 太大會 filter out some features (under-fit)?
策略:同時使用角度 maximize $\theta$ and Magnitude minimize $|w|$!
Magnitude margin: 增加 inter-class margin? Angle margin: compress intra-class? 先 push 角度,再 push w, 再角度, …. 角度 m, make it differentiable!
To Do
- check the SVM, check the logistic regression, check import vector
- Use binary classification as an example
- Pro and Con of the three types.
- Most importantly, try to use both amplitude and angle for learning!! TBD
Reference
Liu, Weiyang, Yandong Wen, Zhiding Yu, Ming Li, Bhiksha Raj, and Le Song. 2018. “SphereFace: Deep Hypersphere Embedding for Face Recognition.” January 29, 2018. http://arxiv.org/abs/1704.08063.
Liu, Weiyang, Yandong Wen, Zhiding Yu, and Meng Yang. 2017. “Large-Margin Softmax Loss for Convolutional Neural Networks.” November 17, 2017. http://arxiv.org/abs/1612.02295.
Rashad, Fathy. n.d. “Additive Margin Softmax Loss (AM-Softmax).” Medium. Accessed December 27, 2020. https://towardsdatascience.com/additive-margin-softmax-loss-am-softmax-912e11ce1c6b.
Wang, Feng, Weiyang Liu, Haijun Liu, and Jian Cheng. 2018. “Additive Margin Softmax for Face Verification.” May 30, 2018. https://doi.org/10.1109/LSP.2018.2822810.