CV-SLAM Feature Extraction - SIFT/SURF/ORB

Posted on | In

Reference

[@jadenHarrisCorner2011] : excellent intuition of Harris and SIFT feature extraction

[@wikiScaleinvariantFeature2022] : wiki SIFT

[@liuSIFTFeature2016] : focus on SIFT, similar to Wiki SIFT

[@lowkeyway42Key2021] : lots of intuition of ORB!

前言

有兩類 feature extraction: (1) low level feature extraction: 一般是先找到具有 “某些特性” 的特徵點或關鍵點，例如 corner, edge, 等等有比較大亮度或顔色對比點。但並不一定伴隨 object detection 的功能（但可能根據特徵點再做 object detection）；(2) high level feature extraction: 通常伴隨 object detection 同時找出特徵點, 例如 face detection 的 feature point extraction; 或是 hand tracking 的 key point extraction.

(1) 多半是傳統的 CV 算法；(2) 則已經轉爲深度學習 NN 算法。當然不是絕對，例如 optical flow 可以視爲 low level feature extraction + motion, 可以是 CV 或是 NN 算法。

一個問題就是所謂特徵點要滿足 “某些特性” 如何定義? 直覺來説

  • Distinctive: 特徵點需要某一種足夠的對比，i.e. “significant” gradient, 例如亮點或顔色的變化。一面白墻的每一點基本沒有提供任何有用的 “特徵”。簡單說就是特徵點的檢測。
  • Invariant: 這些特徵點不會隨著操作而消失或改變。操作可以是移動、旋轉、尺度放大或縮小。也就是 invariant 不變性。簡單說就是特徵點的描述。
  Low level feature extraction High level feature extraction
Example corner, by light or color gradient face, hand, by object
Scope local local + global?
Algorithm CV (or NN sometimes) NN
Invariant Scale, Rotation Scale, Rotation, but allow distortion?

可以用 SSL for feature extraction 嗎?

CV Feature Extraction

重點是 invariant: scale invariant, rotation invariant. and argument invariant?

SIFT : Scale-Invariant Feature Transform

SIFT 是一種計算機視覺的特征提取算法，用來偵測與描述圖像中的局部性特征。

Input: 2D image; Output : key points which are invariant with respect to scale, lighting, etc.

實質上，它是在不同的尺度空間 (scale space) 上查找關鍵點 (特征點)，並計算出關鍵點的方向。SIFT所查找到的關鍵點是一些十分突出、不會因光照、仿射變換和噪音等因素而變化的點，例如角點、邊緣點、暗區的亮點及亮區的暗點等。

SIFT 特徵提取步驟 （Step 1-3: 特徵點檢測; Step 4-5: 特徵點描述）

Step 1: 尺度空間 (scale space) 生成

這和 Laplace transform 或是 Fourier transform 是類似的觀念。尺度空間理論目的是模擬圖像的多尺度特徵，Gauss kernel 是實現尺度變換的 linear kernel. 一個 2D 圖像的尺度空間定義指一個變化尺度 ($\sigma$) 的二維高斯函數 $G(x,y,\sigma)$ 與原圖像 $I(x,y)$ 卷積（即高斯模糊，Gaussian Blur）後形成的空間：
\(L(x, y, \sigma)=G(x, y, \sigma) * I(x, y)\)

其中, $G(x, y, \sigma)$ 是尺度變換高斯函数, $G(x, y, \sigma)=\frac{1}{2 \pi \sigma^{2}} e^{-\left(x^{2}+y^{2}\right)} / 2 \sigma^{2}$.

$(x, y)$ 是空間坐標，$\sigma$ 是尺度坐標。$\sigma$ 是連續值，值的大小決定圖像的平滑程度：大尺度對應圖像的低頻 (概貌) 特徵，小尺度對應圖像的高頻細節特徵。

再來定義 DoG (Difference of Gauss) 尺度空間，DoG scale space: ($k$ 一般是 fixed parameter) \(D(x, y, \sigma)=(G(x, y, k \sigma)-G(x, y, \sigma)) * I(x, y)=L(x, y, k \sigma)-L(x, y, \sigma)\) 下圖是一個例子。上半部是 $L(x,y,\sigma)$, w.r.t. 5 different $\sigma$ and $k=1 \text{ or } \sqrt[3]{2}\sim 1.26$, 一共有 10 個圖。左上是最小的 $\sigma$ and $k=1$. 越往右邊 $\sigma$ 越大所以越模糊（概貌）。第二排對應 $k=\sqrt[3]{2}$，所以比第一排更模糊。

下半部則是 $G(x,y,\sigma)$, 對應第二排減去第一排，有一點負片的效果。越左邊輪廓約淡，因爲 $\sigma \sim 0 \to G(x,y, 2\sigma) \sim G(x,y,\sigma) \to D(x,y, \sigma) \sim 0 $

越右邊則 $\sigma$ 越大，雖然圖變模糊但是上下圖比較有差異，所以上下相減比較接近上圖的負片。

以下圖而言，$\sigma = 1.6$ (中間圖) 是一個比較好的 trade-off for feature extraction and invariant to $\sigma$ difference to certain extent。 也就是說，我們用 $\sigma = 1.6$ 所找的的 feature points 對於其他的 $\sigma$ 應該也是 feature points.

image-20220417220541461

Step 2: 尺度空間的極值檢測

尺度空間指一個變化尺度 (σ) 的二維高斯函數 G(x,y,σ) 與原圖像 I(x,y) 卷積（即高斯模糊，Gaussian Blur）後形成的空間。尺度不變特征應該既是空間域 (spatial domain) 上又是尺度域 (scale domain) 上的局部極值。極值檢測的大致原理是根據不同尺度下的高斯模糊化圖像差異（Difference of Gaussians, DoG）尋找局部極值，這些找到的極值所對應的點被稱為關鍵點或特征點。

Question: 爲什麽局部極值是關鍵點？ Answer: 因爲斜率為 0，基本就是 local scale-invariant and spatial invariant points!

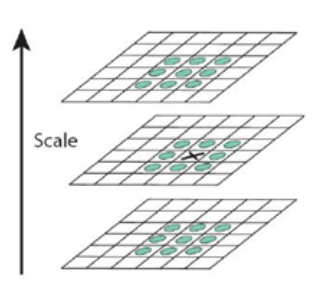
爲了尋找 (DOG) 尺度空間的極值點。每一個采樣點要和它所有相鄰點比較，看其是否比它 spatial domain 和 scale domain 的相鄰點大或小。

如下圖，中間的檢測點必須和它同尺度的 8 個相鄰點和上下相鄰尺度的 9x2 共 26 點比較，以確保在尺度空間和二維圖像空間都是極值點。

重點來了：如果一個點在 DOG 尺度空間以及上下兩層的 26 個相鄰點都是最大或是最小值時，就認爲該點是在該尺度下的一個特徵點。

image-20220417225136662

Step 3: 精確定位關鍵點（極值點）

在不同尺寸空間下可能找出過多的關鍵點，有些關鍵點可能相對不易辨識或易受噪聲幹擾。該步借由關鍵點附近像素的信息、關鍵點的尺寸、關鍵點的主曲率來定位各個關鍵點，借此消除位於邊上或是易受噪聲幹擾的關鍵點。

通過 fitting 三維二次函數以精確確定關鍵點的 (二維) 位置和 (一維) 尺度達到 sub-pixel 的精度，同時去除低對比度的關鍵點和不穩定的邊緣響應點 (因爲 DoG 算子會產生較强的邊緣響應)，以提高抗噪聲能力。

  • 空間尺度函數的二階導數為 0, 得到精确的位置 $\hat{x}$.
\[D(x, y, \sigma) \approx D(x, y, \sigma)+\frac{\partial D^{T}}{\partial x} x+\frac{1}{2} x^{T} \frac{\partial^{2} D}{\partial x^{2}} x = 0 \\ \hat{x}=-\frac{\partial^{2} D^{-1}}{\partial x^{2}} \frac{\partial D}{\partial x}\]

​ 數學上就是找到曲率為 0 的點，或是 Laplacian 點。

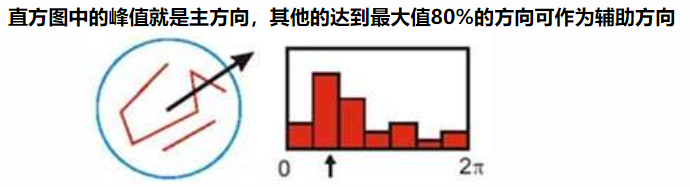
Step 4: 為每個關鍵點的方向定位

Step 1-3 都是在找局部尺度不變的點。為了使 descriptor (見 step 5) 具有旋轉不變性，需要利用圖像的梯度方向分佈為給每一個關鍵點分配一個基準方向。 \(\begin{aligned} &m(x, y)=\sqrt{(L(x+1, y)-L(x-1, y))^{2}+(L(x, y+1)-L(x, y-1))^{2}} \\ &\theta(x, y)=\tan^{-1} ((L(x, y+1)-L(x, y-1)) /(L(x+1, y)-L(x-1, y))) \end{aligned}\) 上式為 $(x,y)$ 梯度的模值和方向公式。其中 $L(x,y)$ 所用的尺度 ($\sigma$) 為每個關鍵點各自所在的尺度。

每個關鍵點有三個信息：位置 (x,y)、所在尺度 ($\sigma$)、方向 ($\theta$)。

利用關鍵點鄰域像素的梯度方向分佈特性為每個關鍵點指定方向參數，使算子具備旋轉不變性。

image-20220418214931023

Step 5: 關鍵點描述子生成

找到關鍵點的位置、尺寸並賦予關鍵點方向後，將可確保其移動、縮放、旋轉的不變性。此外還需要為關鍵點建立一個描述子向量，使其在不同光線與視角下皆能保持其不變性。如何建立描述子向量?

首先將坐標軸旋轉為關鍵點方向，以確保旋轉不變性。以特徵點爲中心取 8x8 的鄰域作爲采樣窗口。將采樣點與特徵點的相對方向通過 Gauss 加權歸入包含 8 個方向直方圖，最後獲得 2x2x8 的 32 維特徵描述子，如下圖。

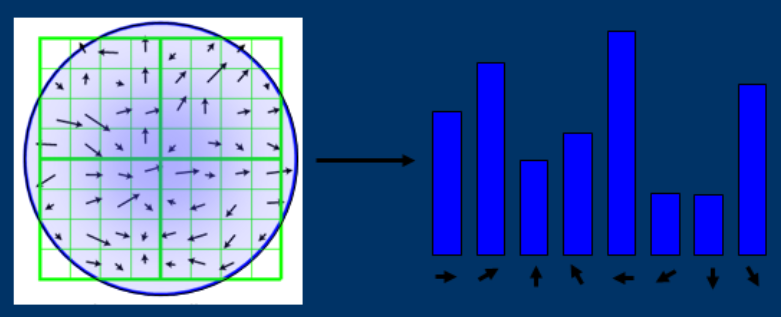
image-20220418214130601

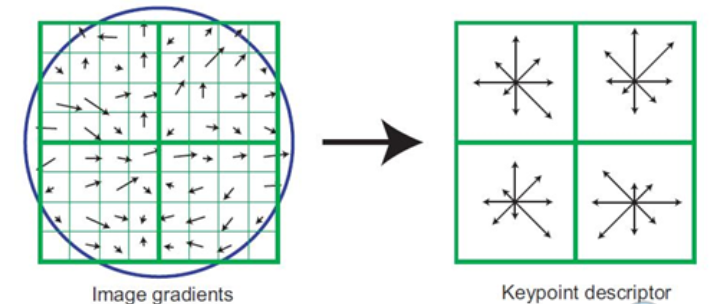
image-20220418215912742

還沒結束。每一個小格都代表特徵點所在的尺度空間的一個像素。然後在 4x4 的窗口内計算 8 個發現的梯度方向直方圖。（實在太複雜！）

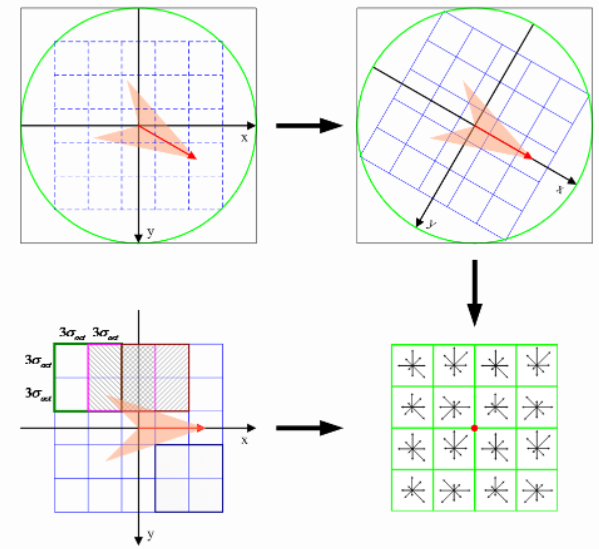
image-20220418220818694

這就導致 SIFT 的特徵向量有 128 維 (4x4x8). 將這個向量歸一之後，就進一步去除了光照的影響。(opencv 中實現的也是 128 維)

image-20220418221309078

image-20220418221240306

Y. Ke 之後把描述子部分用 PCA 代替直方圖，對其進行改進。稱爲 PCA-SIFT 算法。

SURF - Speeded Up Robust Features

SURF 是一種穩健的圖像識別和描述算法。它是SIFT的高效變種，也是提取尺度不變特征，算法步驟與SIFT算法大致相同，但采用的方法不一樣，要比SIFT算法更高效（正如其名）。SURF使用 Hesseian 矩陣的行列式值作特征點檢測並用積分圖加速運算；SURF 的描述子基於 2D 離散小波變換響應並且有效地利用了積分圖。

  1. 特征點檢測： SURF使用Hessian矩陣來檢測特征點，該矩陣是x,y方向的二階導數矩陣，可測量一個函數的局部曲率，其行列式值代表像素點周圍的變化量，特征點需取行列式值的極值點。用方型濾波器取代SIFT中的高斯濾波器，利用積分圖（計算位於濾波器方型的四個角落值）大幅提高運算速度。
  2. 特征點定位： 與SIFT類似，通過特征點鄰近信息插補來定位特征點。
  3. 方向定位： 通過計算特征點周圍像素點x,y方向的 Haar wavelet 變換，並將x,y方向的變換值在xy平面某一角度區間內相加組成一個向量，在所有的向量當中最長的(即x、y分量最大的)即為此特征點的方向。
  4. 特征描述子： 選定了特征點的方向後，其周圍相素點需要以此方向為基準來建立描述子。此時以5x5個像素點為一個子區域，取特征點周圍20x20個像素點的範圍共16個子區域，計算子區域內的x、y方向(此時以平行特征點方向為x、垂直特征點方向為y)的 Haar wavelet 轉換總和Σdx、ΣdyΣdx、Σdy與其向量長度總和Σ dx 、Σ dy Σ dx 、Σ dy 共四個量值，共可產生一個64維的描述子。

ORB - Oriented FAST and Rotated BRIEF

[@rubleeORBEfficient2011] and [@lowkeyway42Key2021]

運行過SIFT 或 Harris，一定有所感悟。即便它集尺度不變、旋轉不變、光變不敏感等優點於一身，但是它運行實在是慢了點。

那麽改善SIFT，從SURF開始，大家的重點都是集中在速度優化上。據論文中提供，ORB要比SIFT快兩個數量級！

這麽厲害，我們先了解一下啥是ORB。

什麽是ORB

ORB（Oriented FAST and Rotated BRIEF）是 Oriented FAST + Rotated BRIEF 的縮寫（感覺應該叫OFRB）。是目前最快速穩定的特征點檢測和提取算法，許多圖像拼接和目標追蹤技術利用ORB特征進行實現。

先記住我們的初衷：

首先要實現目標檢測的功能； 其次在不犧牲性能的代價下提高速度； 最後，開源無專利； 大神們在ORB上都做到了！

ORB = Oriented FAST (特徵點, distinctive) + Rotated BRIEF (特徵點描述, invariant)

ORB（Oriented FAST and Rotated BRIEF）該特征檢測算法是在著名的 FAST 特征檢測和 BRIEF 特征描述子的基礎上提出來的，其運行時間遠遠優於 SIFT 和 SURF，可應用於實時性特征檢測。ORB特征檢測具有尺度和旋轉不變性，對於噪聲及其透視變換也具有不變性，良好的性能是的利用ORB在進行特征描述時的應用場景十分廣泛。ORB特征檢測主要分為以下兩個步驟: (1) Oriented FAST 特征點檢測 (distinctive)；(2) Rotated BRIEF 特征點描述 (invariant)。

有很多圖像特征檢測算子，我們可以用 LoG 或者 DoG 檢測圖像中的Blobs（斑點檢測），可以根據圖像局部的自相關函數來求得 Harris 角點（Harris 角點），又提到了兩種十分優秀的特征點及它們的描述方法 SIFT 特征與 SURF特征。SURF 特征算是為了提高運算效率對SIFT特征的一種近似，雖然在有些實驗環境中已經達到了實時，但是我們實踐工程應用中，特征點的提取與匹配只是整個應用算法中的一部分，所以我們對於特征點的提取必須有更高的效率要求，從這一點來看前面介紹的的那些特征點方法都不可取。

為了解決這個問題，Edward Rosten 和 Tom Drummond 在2006年發表的“Machine learning for high-speed corner detection”文章中提出了一種 FAST 特征，並在 2010 年對這篇論文作了小幅度的修改後重新發表。FAST 的全稱為 Features From Accelerated Segment Test。Rosten 等人將 FAST 角點定義為：若某像素點與其周圍領域內足夠多的像素點處於不同的區域，則該像素點可能為角點。也就是某些屬性與眾不同，考慮灰度圖像，即若該點的灰度值比其周圍領域內足夠多的像素點的灰度值大或者小，則該點可能為角點。

FAST 原理 (Features from Accelerated Segment Test)

FAST，正如其名。它的出現就是為了解決SIFT在建立特征點時速度慢的問題。要解 bug 首先要做的是定位問題。

SIFT為什麽慢？

SIFT進行特征點檢測時需要建立尺度空間，基於局部圖像的梯度直方圖來計算描述子，整個算法的計算和數據存儲覆雜度比較高，不適用於處理實時性很強的圖像。

FAST的解決方案是什麽？

若某像素與其周圍領域內足夠多的像素點相差較大，則該像素可能是特征點。

如何用算法實現？

海選 + 篩選。

Step1: 確定候選角點（corner point, Segment Test）

  1. 選擇某個像素 $p$ ， 其像素值為 $I_p$ 。以 $p$ 為圓心，半徑為3， 確立一個圓，圓上有16個像素，分別為 $p_1, p_2, …,, p_{16}$
  2. 確定一個閾值：$t$ (比如 $I_p$ 的 20%)。
  3. 讓圓上的像素的像素值分別與 $p$ 的像素值做差，如果存在連續 n 個點滿足 $I_x - I_p > t$ 或 $I_x - I_p < -t$ （其中 $I_x$ 代表此圓上16個像素中的一個點），那麽就把該點作為一個候選點。根據經驗，一般令n=12 (n 通常取 12，即為 FAST-12。其它常用的 N 取值為 9 和 11， 他們分別被稱為 FAST-9，FAST-11).

image-20220420222617620

由於在檢測特征點時是需要對圖像中所有的像素點進行檢測，然而圖像中的絕大多數點都不是特征點，如果對每個像素點都進行上述的檢測過程，那顯然會浪費許多時間，因此 FAST 采用了一種進行非特征點判別的方法。如上圖中，對於每個點都檢測第1、5、9、13號（即上下左右）像素點，如果這4個點中至少有3個滿足都比 $I_p + t$ 大或者都比 $I_p - t$ 小，則繼續對該點進行16個鄰域像素點都檢測的方法，否則則判定該點是非特征點（也不可能是角點，如果是一個角點，那麽上述四個像素點中至少有3個應該和點相同），直接剔除即可。

Step2: 非極大值抑制

經過 Step 1 的海選後，還是會有很多個特征點。好在他們有個缺點：很可能大部分檢測出來的點彼此之間相鄰，我們要去除一部分這樣的點。為了解決這一問題，可以采用非最大值抑制的算法：

  • 假設P，Q兩個點相鄰，分別計算兩個點與其周圍的16個像素點之間的差分和為 V。
  • 去除 V 值較小的點，即把非最大的角點抑制掉。

經過上述兩步後FAST特征值篩選的結果就結束了。

Oriented FAST

FAST快是快，但是無法體現出一個優良特征點的尺度不變性和旋轉不變性。

Fast角點本不具有方向，由於特征點匹配需要，ORB對Fast角點進行了改進，改進後的 FAST 被稱為 Oriented FAST，具有旋轉和尺度的描述。

How?

從SIFT過來的我們對這個問題不陌生。

  • 尺度不變性：可以用金字塔解決；

  • 旋轉不變性：可以用質心標定方向解決；

尺度不變性：
  1. 對圖像做不同尺度的高斯模糊
  2. 對圖像做降采樣(隔點采樣)
  3. 對每層金字塔做FAST特征點檢測
  4. n幅不同比例的圖像提取特征點總和作為這幅圖像的oFAST特征點。
旋轉不變性：

  1. 在一個小的圖像塊 B 中，定義圖像塊的矩。

  2. 通過矩可以找到圖像塊的質心

  3. 連接圖像塊的幾何中心 O 與質心 C，得到一個方向向量就是特征點的方向

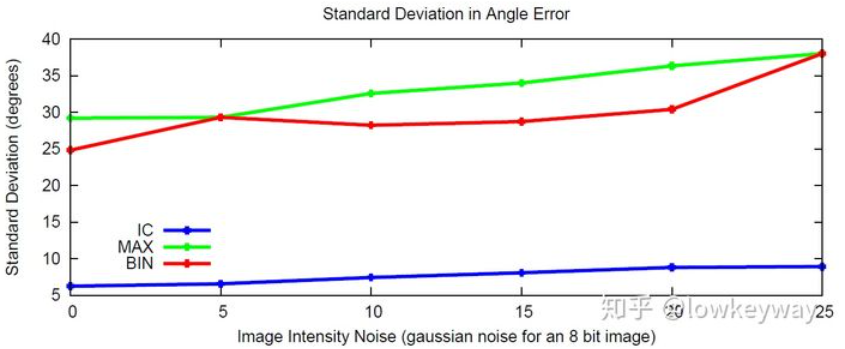
image-20220422211011872

在噪聲的影響下，這種方法 (IC) 比起直方圖 (BIN in SIFT) 或是 MAX 算法相比，都有組好的恢復主方向的性能。

BRIEF

BRIEF 是 2010 年的一篇名為 “BRIEF : Binary Robust Independent Elementary Features” 的文章中提出，BRIEF是對已檢測到的特征點進行描述，它是一種二進制編碼的描述子，擯棄了利用區域灰度直方圖描述特征點的傳統方法，采用二級制、位異或運算，大大的加快了特征描述符建立的速度，同時也極大的降低了特征匹配的時間，是一種非常快速，很有潛力的算法。

如果說FAST用來解決尋找特征點的速度問題，那麽BRIEF就用來解決描述子的空間占用冗余問題。

我們知道了BRIEF的實質就是特征點的描述子。那麽前提就是描述對象特征點從何而來？實際上，Harris/FAST/SIFT/SURF等算法提供的特征點都可以用 BRIEF 描述。

1、為減少噪聲幹擾，先對圖像進行高斯濾波（方差為2，高斯窗口為9x9）

2、以特征點為中心，取SxS的鄰域窗口。在窗口內隨機選取一對（兩個）點，比較二者像素的大小，進行二進制賦值。

3、在窗口中隨機選取N對隨機點，重覆步驟2的二進制賦值，形成一個二進制編碼，這個編碼就是對特征點的描述，即特征描述子。（一般N=256）

這5種方法生成的256對（OpenCV中用32個字節存儲這256對）隨機點如下（一條線段的兩個端點是一對）：

image-20220422211818929

經過上面三個步驟，我們就可以為每個特征點表示為一個 256bit 的二進制編碼。

Rotated BRIEF

一個問題：描述子是用來描述一個特征點的屬性的，除了標記特征點之外，它最重要的一個功能就是要實現特征點匹配。BRIEF 的二進位 binary value 是如何實現特征點匹配的呢？

**答案是：Hamming distance! 不是 A-B 而是 element-wise XOR**
  • 兩個特征編碼對應bit位上相同元素的個數小於128的，一定不是配對的。
  • 一幅圖上特征點與另一幅圖上特征編碼對應bit位上相同元素的個數最多的特征點配成一對。Element-wise XOR.

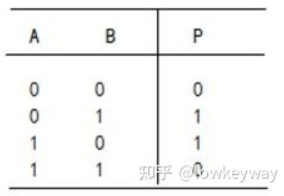
image-20220422214843324

所以，對於BRIEF來說，描述子裏不包含旋轉屬性，所以一旦匹配圖片有稍微大點的旋轉角度，按照Hamming算法，匹配度將會大幅下降。

詳細做法查看 reference.

至此，ORB的優化就結束了。我們嘗試總結一下：

  • FAST是用來尋找特征點的。ORB在FAST基礎上通過金字塔、質心標定解決了尺度不變和旋轉不變。即oFAST。
  • BRIEF是用來構造描述子的。ORB在BRIEF基礎上通過引入oFAST的旋轉角度和機器學習解決了旋轉特性和特征點難以區分的問題。即rBRIEF.

現在，有了特征點尋找和描述子，ORB就成了！

直接使用 OpenCV 的 ORB for feature extraction and match (with 90 degree rotation and 75% scaling), 結果如下：

image-20220423104009627

SIFT vs. SURF vs. ORB

[@pereraComparisonSIFT2018] 有一個簡單的測試。只有旋轉 180 度的 feature extraction and match result:

image-20220422220109287

ORB (ORD is typo) 得到 100% 的結果。同時速度也是最快。

[@kennerleyComparisonSIFT2021] 也有類似結果：使用 5 個 images，改變亮度和方向。

image-20220422220605275

##

執行速度的比較 (~300 key points): ORB 大勝

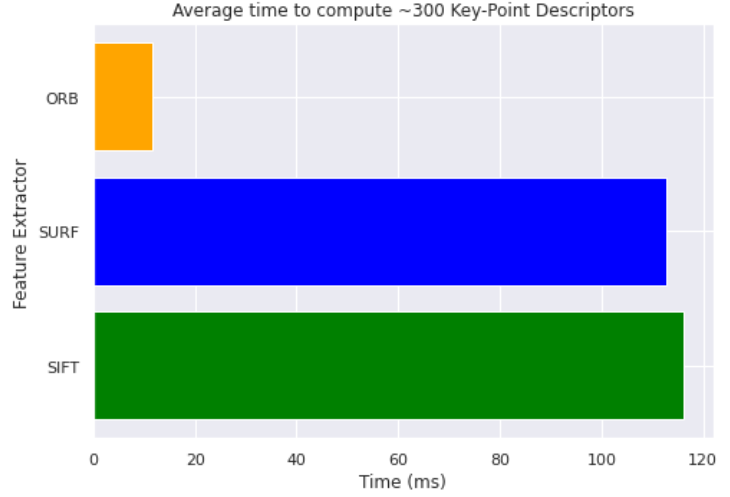
image-20220422220702769

Match percentage: ORB 最優。

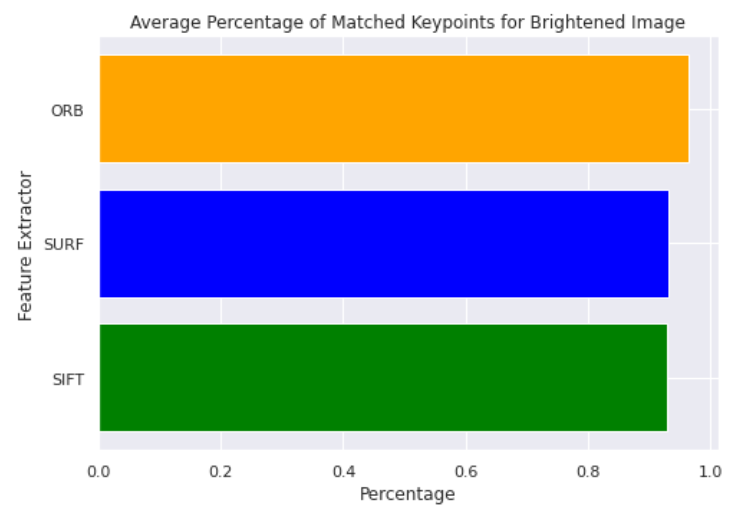
image-20220422220819796

結論： Brute force (ORB) 似乎比起各種數學 (SIFT/SURF) 操作都有效！

Reference