CV-SLAM Bundle Adjustment (BA)

Posted on | In

Reference

[@xiaofanDetailedExplanation2020] : history of BA

[@grapeVSLAMBundle2019] : better explanation of visual BA

[@parraVisualSLAM2019] : more systematic paper

[@triggsBundleAdjustment2000] : comprehensive article

Bundle Adjustment History

Bundle adjustment (BA), 經典的BA目的是優化相機的 pose 和 landmark, 其在 SfM 和SLAM 領域中扮演者重要角色。Bundle adjustment 最早是19世紀由搞大地測量學 (測繪學科) 的人提出來的, 19世紀中期的時候，geodetics 的學者就開始研究 large scale triangulations（大型三角測量）。20世紀中期，隨著camera 和 computer 的出現，photogrammetry (攝影測量學) 也開始研究 adjustment computation，所以他們給起了個名字叫 bundle adjustment。21世紀前後，robotics領域開始興起SLAM，最早用的recursive bayesian filter（遞歸貝葉斯濾波），後來把問題搞成個 graph 然後用 least squares 方法求解。

Bundle adjustment 歷史發展圖如下:

preview

Bundle adjustment 其本質還是離不開 least square principle, 最小平方原理 (Gauss功勞)。幾乎所有優化問題其本質都可以追溯到 least square principle。目前 bundle adjustment 優化框架最為代表的是 ceres solver 和 g2o. 這裏主要介紹 ceres solver.

據說 ceres 的命名是天文學家 Piazzi 閑暇無事的時候觀測一顆沒有觀測到的星星，最後 Gauss 用 least square 算出了這個小行星的軌道，故將這個小行星命名為 ceres，中文翻譯成穀神星。

Bundle Adjustment 算法

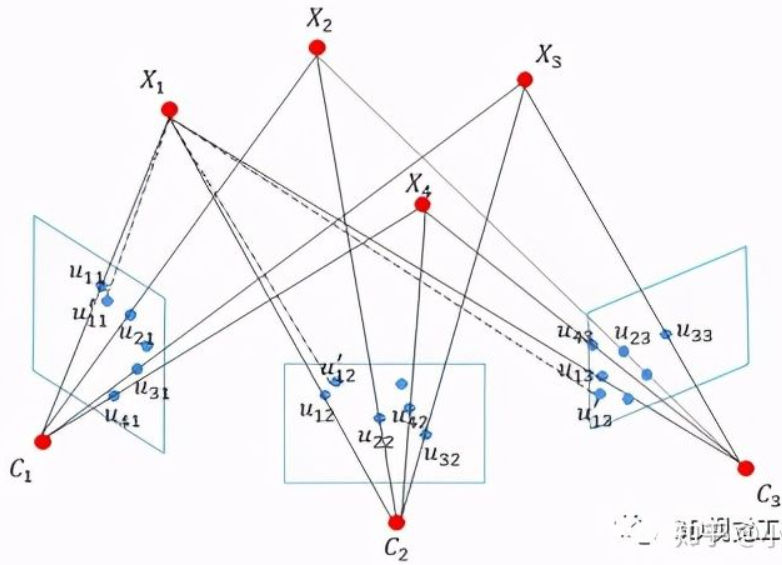
Bundle adjustment 是關於在不同的相機位置 $C_1, C_2, C_3$ 觀察 3D 空間的物體或位置 $X_1 …, X_4$。因爲相機無法記錄深度，只能記錄 2D 平面的 (local) 像素坐標 $u_{ij}$。

我們的目標當然是找出 $X_1$

優化最小平方函數 (error function) 如下,其中 $u_{ij}$ 是投影在二維的像點坐標, $C_j$ 是相機投影矩陣, $\mathrm{X_i}$ 是三維點坐標: \(\min \sum_{i=1}^{n} \sum_{j=1}^{m}\left(u_{i j}-\pi\left(C_{j}, X_{i}\right)\right)^{2}\) 重點是 under certain constraints!

image-20220423205922563

  行星觀測 vSLAM
$X_1, X_2, …$ (global 3D) 每晚一個 $X_i$ 對應行星 3D 位置時間變化 (軌跡地圖) 一般是靜止的 3D (物體)空間地圖 n 個特徵點
$C_1, C_2, …$ (global 3D) 每晚一個 $C_i$ 對應地球 3D 位置時間變化 移動觀察者在 3D 空間位置每幀(時間)的變化，共有 m 幀率
$u_{ij}$ (local 2D) 每晚一個 $u_{ii}$ 對應 2D 測量，一共 K 天個值 每一幀都有 n 個 $u_{ij}$, 共有 m x n 個 $u_{ij}$
Constraint $X_1, X_2, …$ 共平面，並 follow Kepler’s law (with Sun at the focus). $C_1, C_2, …$ 也一樣 $X_1, X_2, …$ 靜止；$C_1, C_2, …$ 滿足 robot 限制

行星觀測

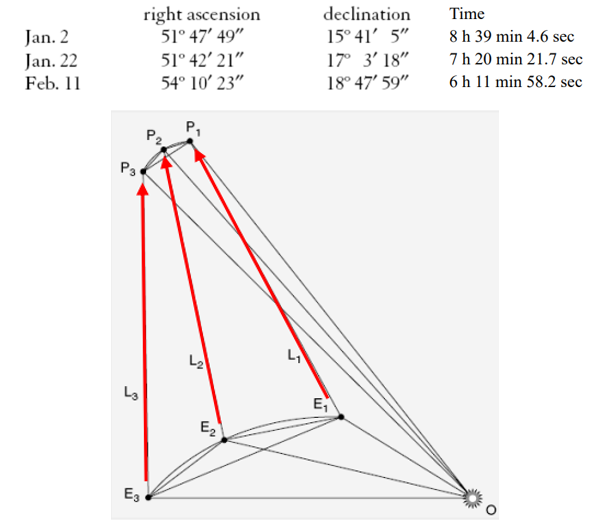
Gauss 只用了三晚的測量，加上 Kepler’s law 就推斷出穀神星的軌道，如下圖。

$P_1, P_2, P_3$ 是穀神星 3D 空間的軌道。$E_1, E_2, E_3$ 是地球 3D 空間的軌道。$u_{11}, u_{22}, u_{33}$ 是 local 2D 的經緯度，如下表。注意我們並不知道深度的資訊，i.e. $L_1, L_2, L_3$. Time measurements 是爲了利用 Kepler’s laws to constrain $P_1, P_2, P_3$ and $E_1, E_2, E_3$.

image-20220425185602420

vSLAM

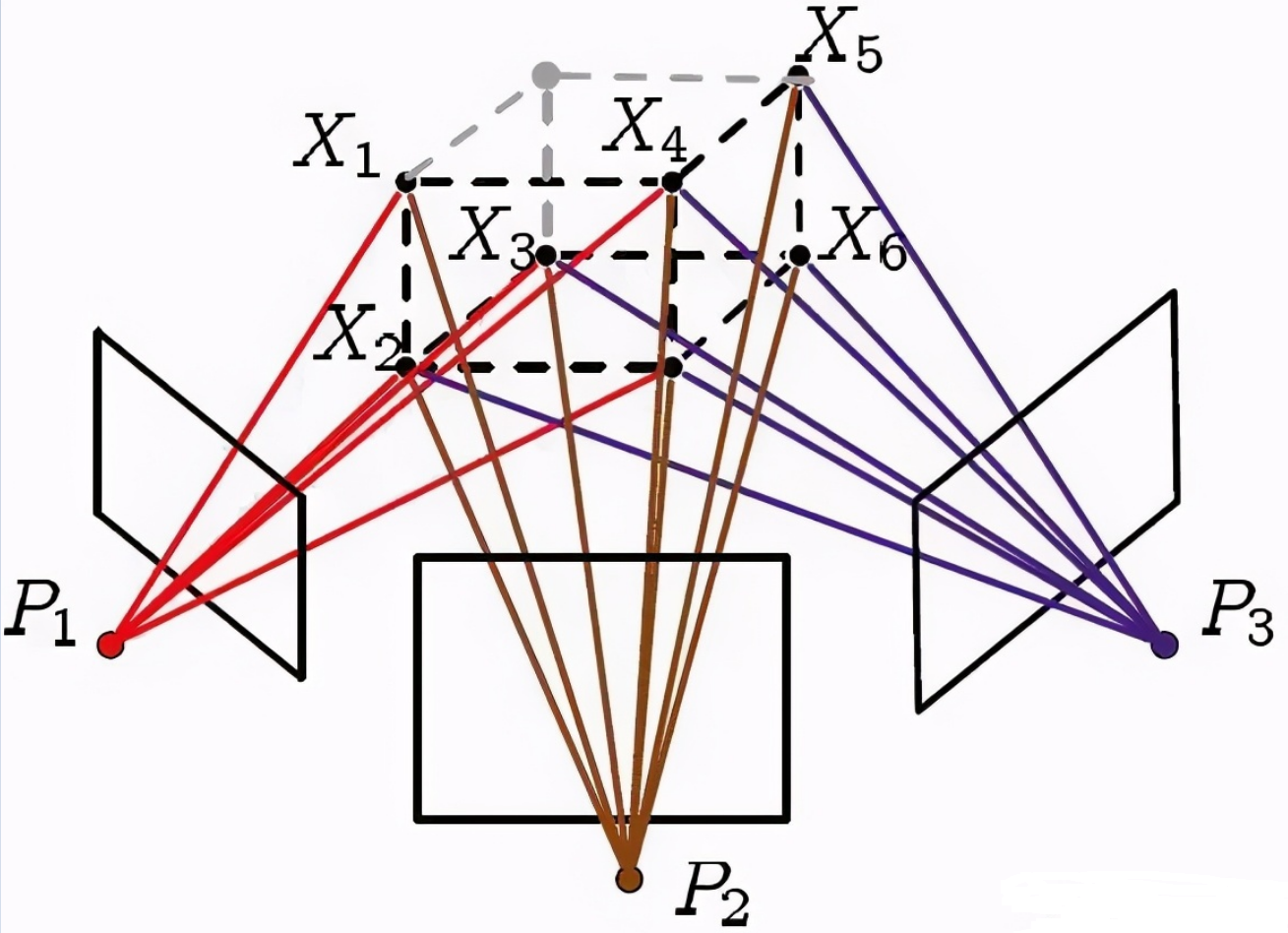
假設空間地圖的 3D 點為 $X_1, X_2, …, X_n$; 相機中心位姿為 $P_1, P_2, …, P_n$.

image-20220424102348130

1.1 地圖點的參數化方式

地圖點的參數化方式主要有兩種：一種是用三維向量 $\mathbf{X} = [x,y,z]^T$ 表達；另一種采用逆深度表達。為了簡單和直觀，我們這裏還是使用比較傳統的三維向量表達。

1.2 相機模型

相機模型也有很多啦，這裏我們同樣是使用最簡單的一種：針孔相機模型。一個3D地圖點 $\mathbf{X}$ 投影到圖像上形成2D像素點 $\mathbf{u}$ (3D global 坐標投影到 2D local 坐標) 可以表示為

\(\lambda \mathbf{u}=\mathbf{K T X}=\left[\begin{array}{ccc} f_{x} & 0 & c_{x} \\ 0 & f_{y} & c_{y} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ll} \mathbf{R} & \mathbf{t} \end{array}\right]\left[\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right]\) 其中 $\mathbf{K}$ 為內參矩陣, $\mathbf{T}$ 為相機的位姿, $\mathrm{X}$ 為 $3 \mathrm{D}$ 地圖點的齊次坐標。我們設定攝像機內至 已知的, 將上述方程簡寫為 \(\mathbf{u}=\pi(\mathbf{T}, \mathbf{X})\) where $\pi(\cdot)$ is the projection function.

$1.3$ 誤差、最小平方問題 我们需要求解的最小平方優化問題為 \(\left\{\mathbf{T}_{i}, \mathbf{X}_{j}\right\}=\arg \min \sum_{\{i, j, k\} \in \chi} \rho\left(\|\underbrace{z_{k}-\pi\left(\mathbf{T}_{i}, \mathbf{X}_{j}\right)}_{\mathbf{e}}\|_{\Sigma}^{2}\right)=\arg \min \sum_{\{i, j, k\} \in \chi} \rho\left(\mathbf{e}^{T} \mathbf{\Sigma}^{-1} \mathbf{e}\right)\)

需要優化的量為相機的位姿 $\mathbf{T}_i$ 和地圖點的位置 $\mathbf{X}_j$ ， $\pi$ 包含了所有的3D-2D投影。 $\mathbf{e}$ 為 cost function，$\rho$ 為魯棒核函數，我們這裏也是用最常用的Huber函數： \(\rho= \begin{cases}x & , \text { if } \sqrt{x}<b \\ 2 b \sqrt{x}-b^{2}, & \text { else }\end{cases}\) 為了便於操作, 這裏我們將其轉換為一個權重 $w$ (這是 g2o 的做法) \(\mathbf{e}^{T}\left(w \boldsymbol{\Sigma}^{-1}\right) \mathbf{e}=\rho\left(\mathbf{e}^{T} \mathbf{\Sigma}^{-1} \mathbf{e}\right)\) 那麽, 權重 $w$ 為 \(w=\frac{\rho\left(\mathbf{e}^{T} \boldsymbol{\Sigma}^{-1} \mathbf{e}\right)}{\mathbf{e}^{T} \boldsymbol{\Sigma}^{-1} \mathbf{e}}\) 至此, 我們需要求解的最小平方優化問題, 變為 \(\left\{\mathbf{T}_{i}, \mathbf{X}_{j}\right\}=\arg \min \sum_{\{i, j, k\} \in \chi} \mathbf{e}^{T}\left(w \mathbf{\Sigma}^{-1}\right) \mathbf{e}\) 1.6 固定部分狀態

對於一個Bundle Adjustment問題，我們必須固定一部分狀態，或者給一部分狀態一個先驗。不然，就會有無窮多解。可以想象一下，一個網絡的誤差已經達到了最小後，可以整體在空間內任意移動，而不會對誤差造成任何影響。我們只要固定這個網絡中的任意1個以上的節點，其他的節點都會有確定的狀態。（我們通常會把第一個位姿固定）

怎麽固定呢？一種可以加一個先驗約束，就是加一個先驗cost function。另外一種就是直接把狀態fix住，不讓它參與優化就好了。 我們采用後一種方法。

具體實現 (Nonlinear least square optimization)

這部分參考 [@parraVisualSLAM2019]，同樣的數學 formulation:

Given a set ${\mathbf{u}{i, j}}$ observations, structure-from-motion (SfM) 是要 estimate 3D scene points 或是地圖點。 The bundle adjustment (BA) formulation 如下： \(\min _{\left\{\mathbf{X}_{i}\right\},\left\{\left(\mathbf{R}_{j}, \mathbf{t}_{j}\right)\right\}} \sum_{i, j}\left\|\mathbf{u}_{i, j}-f\left(\mathbf{X}_{i} \mid \mathbf{R}_{j}, \mathbf{t}_{j}\right)\right\|_{2}^{2},\) where $X = {\mathbf{X}{i}}$ 是 3D 的地圖點；${\mathbf{R}{j}, \mathbf{t}_j}$ 是 6DOF poses of image ${Z_j}$； $f\left(\mathbf{X}{i} \mid \mathbf{R}{j}, \mathbf{t}{j}\right)$ 是 $\mathbf{X}_i$ projection from 3D onto 2D $Z_j$ (calibrated) camera. 實務上不是所有的 $\mathbf{X}_i$ 都是 visible on $Z_j$，所以某些 $(i,j)$ 不存在。

如果 error 是 normal distribution, BA 問題可以視爲 maximum likelihood 問題。

上式是 nonlinear least squares problem. 一般使用 gradient descent methods.

但更有效率的算法是 (1) ceres solver (by Google); 以及 (2) G2O 使用 graphic theory method.

BA-SLAM

嚴格來説，monocular feature-based vSLAM 只是 SfM 變形為 incrementally to process streaming images $Z_{0:t} = {Z_0, Z_1, …, Z_t}$. SLAM optimization based on BA over key frames 算法如下：

image-20220429230015389

幾點説明

  • Step 5: 如果 current frame $Z_t$ 無法在 3D map $X$ 觀察到，可以加入新的 scene points/地圖點。

  • Step 7 (稱爲 local mapping): BA 用來 estimate the camera trajectory and 3D map in the current time window.

  • Step 9 (稱爲 loop closure), a system-wide BA is executed to re-optimize and redistribute accumulated drift errors.

以上只是基本款 SLAM (e.g. ORB-SLAM). 還有很多的細節：例如如何選取 features 和 key frames; 如何 update the co-visibility graph; 如何 select/merge/prune 3D points, etc.