title: Math-AI: Least Square Optimization date: 2022-04-30 09:28:08 categories:
- AI tags: [Optimization, Least square, BA, SLAM] description: Feature Extraction typora-root-url: ../../allenlu2009.github.io —
Reference
[@talakIntroductionNonLinear2020]
Least Square Summary (可以先跳過)
結論如下。簡單來説：
- 如果是 linear least square (one term or sum), 只要用一個大矩陣，使用 Cholesky or QR factorization 求解。
- 如果是 nonlinear least square, 可以用一個大矩陣，找出 gradient (1st order) 或是 Hessian (2nd order) 求解。
- 基本很少用 gradient descent, 一般是 Gauss-Newton, Levenberg-Marquardt, Powell’s dogleg.
- Nonlinear 都會被 linearized, GN/LM 都會 call linear least square solver 例如 Cholesky, QR, etc.
- 如果是 nonlinear least square sum, 有特別的算法如 Ceres or G2O, 可以更 efficiency 求解。
- 其實 G2O solver 也是 call 以上的方法。只是用 graph 作爲 front-end interface.
| One big linear least square | sum of many linear least square’s | One big nonlinear least square | Sum of many nonlinear least square’s | |||
|---|---|---|---|---|---|---|
| Form | $\underset{x \in \mathbb{R}^{n}}{\min}|A x-b|^{2}$ | $\min {x} \sum{i}\left|y_{i}-A_{i} x\right|^{2}$ | $\min|r(x)|^{2}=\sum_{i}\left | r_{i}(x)\right | ^{2}$ | $\min {\mathbf{x}} \sum{i} \rho_{i}\left(\left|f_{i}\left(x_{i_{1}}, \ldots, x_{i_{k}}\right)\right|^{2}\right)$ |
| Solver | (1) Cholesky , or (2) QR | 結合成一個 matrix, 變成左式 | (1) Gradient descent; or (2) Gauss-Newton | (1) Ceres, or (2) G2O | ||
| Convex | Yes | Yes | No guarantee | No guarantee | ||
| Application | linear fitting | linear fitting | Bundle adjustment, planet trajectory |
Introduction
幾乎所有優化問題其本質都可以追溯到 least square principle。據說 ceres 的命名是天文學家 Piazzi 閑暇無事的時候觀測一顆沒有觀測到的星星，最後 Gauss 用 least square 算出了這個小行星的軌道，故將這個小行星命名為 ceres，中文翻譯成穀神星。我們一步一步看。
高中程度 （一元二次方程+微積分）
我們先從宇宙最基本的 optimization function，一元二次方程式開始：$y = x^2$ , 或者改寫成 $y = |f(x)|^2$ where $f(x) = x$
\[\arg_x \min \|f(x)\|^2\]最小值當然是 $y$ 的一階導數為 0, i.e. $x=0$; 另外從 $y$ 的二階導數可以看出是 convex，$y’’ = 2 |f’(x) |^2 + 2 f’‘(x) f(x) >0$。
大學程度（統計綫性迴歸）
此時問題的性質改變。給定很多測量或統計 $(x_i, y_i)$, 我們想要找到一條直綫 $f(x) = a x + b$ 使得”誤差最小“，如下圖。
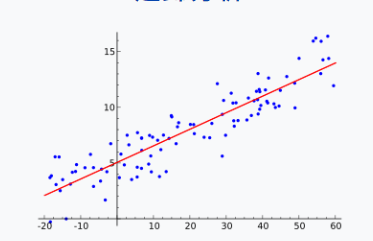\(\arg_{a,b} \min \sum_i \| y_i - (a x_i + b) \|^2 = \arg_{a,b} \min \sum_i \| e_i \|^2 = S(a, b) \label{lqerr}\)
where $e_i = y_i - (a x_i + b)$
幾個重點 :
- 此處把函數的極小值變成誤差平方的極小值。一方面是平方函數的極小值非常容易計算和驗證 (一階和二階導數)。再者平方誤差對應 normal distribution 的 maximum (log)-likelihood solution.
- 此處把原來解函數, $y’ = 0$ or $f(x) f’(x) = 0$, 變成 multiple points overfitting + error sum minimization problem. 注意此處 error 是很多 error term 的平方和。 最後還是解 $\frac{\partial S}{\partial a} = \frac{\partial S}{\partial b} = 0$
- 此處是 1D 的 regression, 可以直接推廣到高維 regression $y = f(x_1, x_2, …, x_n)$.
Example 1 (from wiki):
某次實驗得到了四個數據點 (x,y)：(1,6), (2,5), (3,7), (4,10)（右圖紅色的點）。我們希望找出一條和這四個點最匹配的直線 $y=\beta_{1} + \beta_{2}x$
\(\begin{aligned}
&\beta_{1}+1 \beta_{2}=6 \\
&\beta_{1}+2 \beta_{2}=5 \\
&\beta_{1}+3 \beta_{2}=7 \\
&\beta_{1}+4 \beta_{2}=10
\end{aligned}\)
最小平方法採用的方法是盡量使得等號兩邊的平變異數最小, 也就是找出這個函數的最小值：
\(\begin{aligned}
S\left(\beta_{1}, \beta_{2}\right)=& {\left[6-\left(\beta_{1}+1 \beta_{2}\right)\right]^{2}+\left[5-\left(\beta_{1}+2 \beta_{2}\right)\right]^{2} } \\
&+\left[7-\left(\beta_{1}+3 \beta_{2}\right)\right]^{2}+\left[10-\left(\beta_{1}+4 \beta_{2}\right)\right]^{2}
\end{aligned}\)
最小值可以通過對 $S\left(\beta_{1}, \beta_{2}\right)$ 分別求 $\beta_{1}$ 和 $\beta_{2}$ 的偏導數，然後使他們等於零得到。
\(\begin{aligned}
&\frac{\partial S}{\partial \beta_{1}}=0=8 \beta_{1}+20 \beta_{2}-56 \\
&\frac{\partial S}{\partial \beta_{2}}=0=20 \beta_{1}+60 \beta_{2}-154
\end{aligned}\)
如此就得到了一個只有兩個末知數的方程組, 很容易就可以解出:
\(\begin{aligned}
&\beta_{1}=3.5 \\
&\beta_{2}=1.4
\end{aligned}\)
也就是說直線 $y=3.5+1.4 x$ 是最佳的。
研究所程度（estimation theory, nonlinear least square optimization, bundle adjustment）
注意這裏的 $x$ and $z_j$ 又和前面的定義不同。沒有注意會非常 confusing!
-
$\mathbf{x}$: 這是我們要找的 (fixed and hidden) parameter 類似 linear regression 的 {a, b} to maximize likelihood 或是 minimize error.
-
$\mathbf{z}_j$: 這是一堆的 measurements including noise, 類似 linear regression 的 $(x_j, y_j)$ pair.
Estimation theory 可以是 linear regression 的推廣。Assume we are given N measurements $\mathbf{z}1, \mathbf{z}_2, …, \mathbf{z}_N$ that are function of a variable to estimate $\mathbf{x}$ (e.g. camera poses, 行星軌道)。 Assume that we are also given the conditional distributions: $\mathbb{P}(\mathbf{z}{j} \mid \boldsymbol{x})$
The maximum likelihood estimator (MLE) is defined as: \(\boldsymbol{x}_{\mathrm{MLE}}=\underset{\boldsymbol{x}}{\arg \max } \,\mathbb{P}\left(\mathbf{z}_{1}, \ldots, \mathbf{z}_{N} \mid \boldsymbol{x}\right) \quad \begin{gathered} \text { Measurement } \\ \text {likelihood } \end{gathered}\) where $\mathbb{P}\left(\boldsymbol{z}{1}, \ldots, \boldsymbol{z}{N} \mid \boldsymbol{x}\right)$ is also called the likelihood of the measurements given $\boldsymbol{x}$. 一般更常用的是 minimize negative log-likelihood： \(x_{\mathrm{MLE}}=\underset{\boldsymbol{x}}{\arg \min }\,\,{-\log \mathbb{P}\left(\mathbf{z}_{1}, \ldots, \mathbf{z}_{N} \mid \boldsymbol{x}\right)} \quad \begin{gathered} \text { Negative } \\ \text {log-likelihood } \label{loglike} \end{gathered}\) 上式如果假設 (i) 所有的 $\mathbf{z}_j = (x_j, y_j)$ 都在一個 linear line/plane/space, i.e. $y_j = a x_j + b + n_j$. 反而 $\refeq{loglike}$ 的 $\mathbf{x} = {a,b}$ 是求解的 hidden parameters, notation 很亂 ; (ii) $n$ 是 additive, zero-mean, normal distribution noise; 就會變成 $\refeq{lqerr}$, linear least square optimization.
當然在比較 general 的情況下，$x$ 和 $y$ 不必是 linear relationship. 可以是 nonlinear relationship，$y = f(x) + n$. 如果還是假設 additive, zero-mean, normal distribution noise, 就是 nonlinear least square optimization.
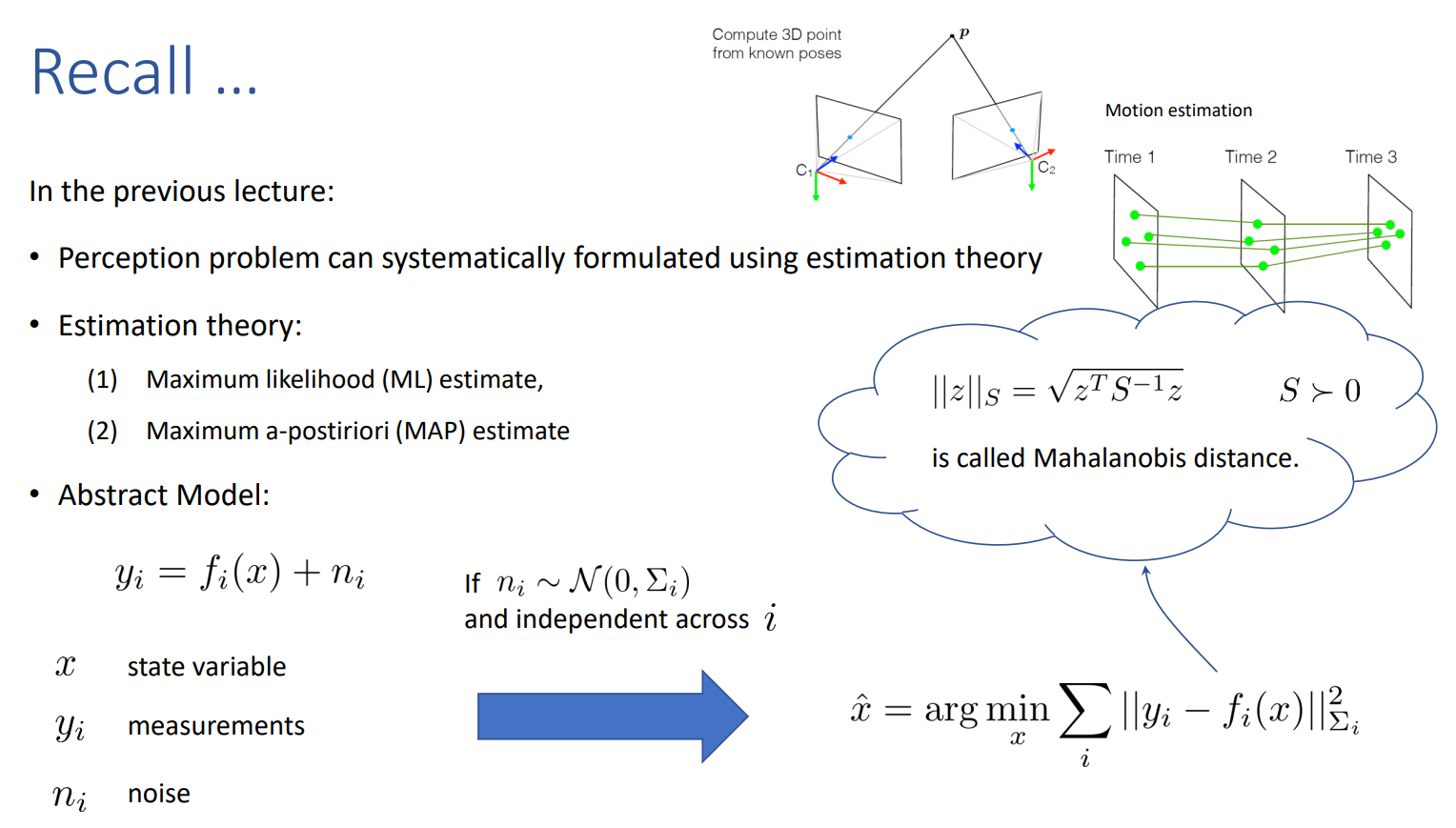
For linear model: \(\hat{x}=\arg \min _{x} \sum_{i}\left\|y_{i}-A_{i} x\right\|_{\Sigma_{i}}^{2}\) 再和 linear regression 對比：
- Measurement with noise 是放在 ${y_i, A_i, \Sigma_i}$. 不是在 ${y_i, x}$ !!!!!
- Hidden parameter 是 $\mathbf{x}$ vector. 如果是 1D linear, $x \sim {a, b}$.
- 另一個小 trick, 就是把 bias b 變成 x 的一部分，稱爲 homogeneous , $A_i$ 只要加上 additional row 1 (見下列).
- 後面我們會再把上式的 summation 結合成一個更大的 matrix，利用 Euclidean distance 特性或是 Mahalanobis distance.
- 下式就是把一堆平方誤差和，變成一個更大的 matrix form。
爲了和之前的平方誤差和形式比較，參考下例：
Example 2 (重複 Example 1, 但用 the new way):
我們把 example 1 用 linear least square 方法重新做一次。其中 n = 2 (2D linear function) and m = 4 (data points)。 \(\begin{aligned} r(x) = A x - b &= {\left[\begin{array}{ll} 1 & 1 \\ 1 & 2 \\ 1 & 3 \\ 1 & 4 \end{array}\right]\left[\begin{array}{l} \beta_{1} \\ \beta_{2} \end{array}\right]-\left[\begin{array}{c} 6 \\ 5 \\ 7 \\ 10 \end{array}\right]} \\ \|r(x)\|^2 &=\|A x-b\|^{2} \end{aligned}\)
Linear Least Squares Problem
也就是說 \(\underset{x \in \mathbb{R}^{n}}{\operatorname{Minimize}}\|r(x)\|^{2}=\sum_{i=1}^{m}\left|r_{i}(x)\right|^{2}\)
- $r: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ and $r(x)=\left[r_{1}(x), r_{2}(x), \ldots r_{m}(x)\right]^{T}$ n = 2 for 2D linear regression
- $r_{i}(x)$ is the residual function or error function
- if $r(x)=A x-b$ we call it linear least squares problem
注意我們把 summation 拿掉，把 A, b 變成更大的 matrix. \(\underset{x \in \mathbb{R}^{n}}{\operatorname{Minimize}}\|A x-b\|^{2}\)
- $A \in \mathbb{R}^{m \times n}$ and $b \in \mathbb{R}^{m}$
- The objective function is convex! \(\nabla^{2} g(x)=2 A^{T} A \succeq 0\)
- Gradient descent algorithm converges to the global minimum \(x_{t+1}=x_{t}-2 \alpha_{t} A^{T}\left(A x_{t}-b\right)\)
-
But, we can do much better (computationally) by exploiting the problem structure and using the optimality conditions
- Recall: $x$ is a global minima $\Leftrightarrow \nabla g(x)=0$ and $\nabla^{2} g(x) \succeq 0$
- $\nabla g(x)=A^{T} A x-A^{T} b$
- $x$ is a global minima $\Leftrightarrow A^{T} A x=A^{T} b$
How to Solve Linear Least Square Problem?
Method 1: 直接做反矩陣。不是好解法，因爲計算量大 (N^3?)，并且 ill-condition 會造成 numerical unstability.
Method 2: Cholesky solver
\[\left(A^{T} A\right) x=A^{T} b\] \[L=\left(\begin{array}{c:cc} \ell_{11} & 0 & 0 \\ \hdashline \ell_{21} & \ell_{22} & 0 \\ \hdashline \ell_{31} & \ell_{32} & \ell_{33} \end{array}\right)\]- Assuming $A^{T} A \succ 0$
- Cholesky decomposition of $A^{T} A$
where $L$ is a lower triangular and thus $L^{T}$ is an upper triangular matrix
\[\left(L L^{T}\right) x=A^{T} b\]兩步解以上方程式：
- Forward substitution: $L y = A^{T} b$
- Backward substitution: $L^T x= y$
Example 2 continue:
\(\begin{aligned} &\mathbf{A}^T \mathbf{A} \mathbf{x} =\mathbf{L} \mathbf{L}^{T} \mathbf{x} = \mathbf{A}^T b \\ &\left(\begin{array}{ll} 4 & 10 \\ 10 & 30 \end{array}\right) \mathbf{x} =\left(\begin{array}{ll} 2 & 0 \\ 5 & \frac{2889}{1292} \end{array}\right) \times\left(\begin{array}{ll} 2 & 5 \\ 0 & \frac{2889}{1292} \end{array}\right) \mathbf{x} =\left(\begin{array}{ll} 28 \\ 77 \end{array}\right) \end{aligned}\) $(y_1, y_2) = (14, \frac{7\times 1292}{2889})$ and $(\beta_1, \beta_2) = (7-\frac{35\times 1292^2}{2\times 2889^2} , \frac{7 \times 1292^2}{2889^2})$ = (3.5, 1.4)
結果和 Example 1 一樣。
Method 2: QR solver
\(\left(A^{T} A\right) x=A^{T} b\)
-
Perform QR factorization of $A^{T} A$ \(A^{T} A=Q R\) where $Q \in \mathbb{R}^{n \times n}$ s.t. $Q^{T} Q=I$ and $R \in \mathbb{R}^{n \times n}$ is upper triangular
- QR is slower than Cholesky
- QR gives better numerical stability than Cholesky
Back to Nonlinear Least Squares Problem
How to Solve Nonlinear Least Square Problem?
Special case n = 1
n dimension
where \(\nabla g(x)=\left(\begin{array}{c} \frac{\partial g}{\partial x_{1}} \\ \frac{\partial g}{\partial x_{2}} \\ \vdots \\ \frac{\partial g}{\partial x_{n}} \end{array}\right) \quad \nabla^{2} g(x)=\left(\begin{array}{cccc} \frac{\partial^{2} g}{\partial x_{1}^{2}} & \frac{\partial^{2} g}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} g}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} g}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} g}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} g}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} g}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} g}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} g}{\partial x_{n}^{2}} \end{array}\right)\)
Method 1: gradient descent (1st order)
Method 2: Gauss-Newton Method (2nd order)
- $r: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ and $r(x)=\left[r_{1}(x), r_{2}(x), \ldots r_{m}(x)\right]^{T}$
- First-order Taylor approximation \(r_{i}(x) \approx r_{i}\left(x_{0}\right)+\nabla r_{i}\left(x_{0}\right)^{T}\left(x-x_{0}\right) \text { for every } i=1,2, \ldots m\) compile them to get \(r(x) \approx r\left(x_{0}\right)+J\left(x_{0}\right)\left(x-x_{0}\right) \quad \text { where } \quad J\left(x_{0}\right)=\left(\begin{array}{c}\nabla r_{1}\left(x_{0}\right)^{T} \\ \nabla r_{2}\left(x_{0}\right)^{T} \\ \vdots \\ \nabla r_{m}\left(x_{0}\right)^{T}\end{array}\right)\) Holds for any $x_{0} \in \mathbb{R}^{n}$
Back to Nonlinear Least Square Again
很多 nonlinear least square 是不容易把 summation 去掉。或是要求 gradient of summation of nonlinear function 不容易。例如在 SfM 或是 bundle adjustment.
此時就有不同的 numerical 算法：例如 Ceres (from Google) or G2O.
Ceres can solve bounds constrained robustified non-linear least squares problems of the form \(\begin{array}{cl} \min _{\mathbf{x}} & \frac{1}{2} \sum_{i} \rho_{i}\left(\left\|f_{i}\left(x_{i_{1}}, \ldots, x_{i_{k}}\right)\right\|^{2}\right) \\ \text { s.t. } & l_{j} \leq x_{j} \leq u_{j} \end{array}\) Problems of this form comes up in a broad range of areas across science and engineering - from fitting curves in statistics, to constructing 3D models from photographs in computer vision.
$\rho_i$ 稱爲 loss function is a scalar function that is used to reduce the influence of outliers on the solution of non-linear least squares problem.
A special case, when $\rho_i(x) = x$, 就變成熟悉的 non-linear least squares problem.
以上的 nonlinear least square optimization 可以用 ceres, G2O, Eigen, 等等 function 求解。我們看一個例子。
[@yoshinoSLAMEssense2021]
G2O Flow Chart
相較於Ceres而言，G2O函數庫相對較為覆雜，但是適用面更加廣，可以解決較為覆雜的重定位問題。Ceres庫向通用的最小二乘問題的求解，定義優化問題，設置一些選項，可通過Ceres求解。
而圖優化 (graph optimization)，是把優化問題表現成圖的一種方式，這裏的圖是圖論意義上的圖。一個圖由若干個頂點,以及連著這些頂點的邊組成。在這裏，我們用頂點表示優化變量，而用邊表示誤差項。
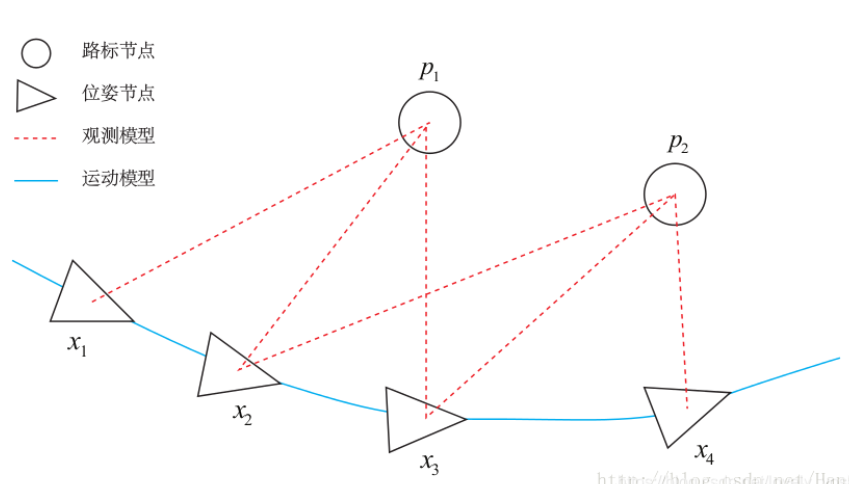
為了使用g2o,首先要將曲線擬合問題抽象成圖優化。這個過程中，只要記住節點為優化變量，邊為誤差項即可。曲線擬合的圖優化問題可以畫成以下形式：
我們直接看 G2O 的 flow chart:
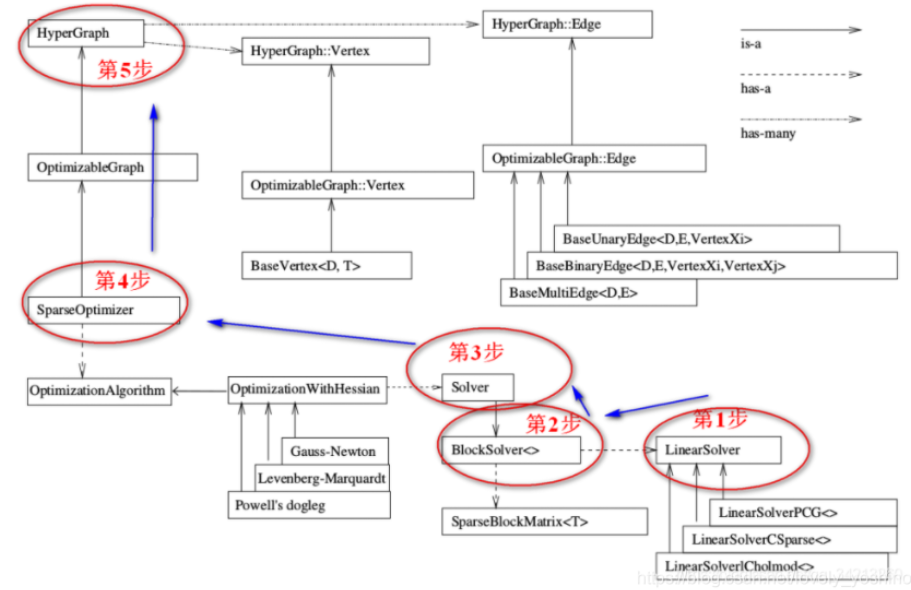
對這個結構框圖做一個簡單介紹（註意圖中三種箭頭的含義（右上角註解））：
（1）整個g2o框架可以分為上下兩部分，兩部分中間的連接點：SparseOpyimizer 就是整個g2o的核心部分。
（2）往上看，SparseOptimizer 其實是一個Optimizable Graph，從而也是一個超圖（HyperGraph）。
（3）$\color{#4285f4}{頂點和邊：}$超圖有很多頂點和邊。頂點繼承自 Base Vertex，用來描述優化的變量。邊用來描述誤差項。
（4）$\color{#4285f4}{配置SparseOptimizer的優化算法和求解器：}$往下看，SparseOptimizer包含一個優化算法部分OptimizationAlgorithm，它是通過OptimizationWithHessian 來實現的。其中叠代策略可以從Gauss-Newton（高斯牛頓法，簡稱GN）、 Levernberg-Marquardt（簡稱LM法）、Powell’s dogleg 三者中間選擇一個（常用的是GN和LM）。
（5）$\color{#4285f4}{如何求解：}$對優化算法部分進行求解的時求解器solver，它實際由BlockSolver 組成。BlockSolver由兩部分組成：一個是SparseBlockMatrix，它由於求解稀疏矩陣(Jocobian和 Hessian)；另一個部分是LinearSolver，它用來求解線性方程 得到待求增量，因此這一部分是非常重要的，它可以從PCG/CSparse/Choldmod選擇求解方法。
在程序中的反應為：
- 創建一個線性求解器LinearSolver。
- 創建BlockSolver，並用上面定義的線性求解器初始化。
- 創建總求解器solver，並從GN/LM/DogLeg 中選一個作為叠代策略，再用上述塊求解器BlockSolver初始化。
- 創建圖優化的核心：稀疏優化器（SparseOptimizer）。
- 定義圖的頂點和邊，並添加到SparseOptimizer中。
最後設置優化參數，開始執行優化。具體的 coding, 可以參考 [@yoshinoSLAMEssense2021]