Floating Point Dynamic Range (DR) and Precision
Floating Point Representation
浮點數可以用以下公式表示:
Normal value (e>0): $f = (-1)^s 2^{e-b} (1+\frac{d_1}{2}+\frac{d_2}{2^2}+\ldots+\frac{d_m}{2^m})\quad$ where $d_i \in {0, 1}$
Subnormal value (e=0) $f = (-1)^s 2^{1-b} (0+\frac{d_1}{2}+\frac{d_2}{2^2}+\ldots+\frac{d_m}{2^m})\quad$ where $d_i \in {0, 1}$
s: sign-bit for mantissa; m: (unsigned) mantissa.
e: (unsigned) exponent, b: fixed exponent bias, 因此 e-b 就會是 signed exponent.
Sign-bit 簡單直觀,是 mantissa 的正負號,和 exponent 正負無關
-
負值只是乘 (-1). 浮點的正負值完全對稱,這和 integer 的 2’s complement 有點不同。
-
所以 floating point 0 有 +0 和 -0! $[000…0] \to +0\,;\quad [100…0]\to -0.$
Unsiged mantissa
Normal value 的 mantissa range: $[1, 2-\frac{1}{2^m}] \sim [1,2)$1 : leading 1 是 default embedded, 沒有 encode 在 mantissa!
- 為什麼 leading 1, mantissa in [1,2), 而不是 leading 0, mantissa in [0, 1)? 因為要確定 floating point representation 唯一。
- Default leading 1 保證不同 exponent value 對應的值域不重疊,並且 mantissa 都在 [1,2) 之間。
- 如果是 leading 0, mantissa 都在 [0,1) 之間。會有 $0.1_2 \times 2^{-2} = 0.01_2 \times 2^{-1}$ 兩者都代表同一浮點數。換句話說,就是不同 exponent value 對應的值域重疊。不但浪費 bit, 也會造成計算困難。
- 如何保證浮點表示唯一?就是要確定 mantissa 的所有值都在一個 octave (8 度) 之內!就是任取兩個值相除 (大除小) 都在 [1,2) 之間 (1 是兩個數字相同)。[1,2) 所有 value 都是在一個 octave, [0,1) 顯然不是, e.g. $0.1_2 / 0.00001_2 > 10_2$ or 2 in 10 進位。
- 為什麼是一個 octave [1,2) 保證唯一? 因為 exponent 的 base 是 2. 所以要小於 2 才不會重疊。如果是 10 進位,就會是 [1, 10), 才能保證唯一,這就是科學記號,$d_1.d_2 d_3 d_4 d_5 \times 10^{k} \quad d_1\in{[1,9]},\, d_{i>1}\in{[0,9]}$
Normal value with leading 1 的最大問題是無法表示 0, ”0“ 和 “1” 是數學最重要的數字!
為了解決這個問題,定義 subnormal value to cover 0.:當 exponent 為 0, mantissa 的 leading 1 變成 leading 0! 這樣就可以表示 0. 因為只有當 exponent = 0 一種 case, 所以不會有值域重疊的問題。
如果只調整 leading 0, 反而造成另一個問題,就是值域不連續:
-
Normal value: (exponent > 0 and mantissa with leading 1): if exponent = 1 $\to f = 2^{1} (1+\frac{d_1}{2}+\frac{d_2}{2^2}+\ldots+\frac{d_m}{2^m}) \in [2, 4)$
-
Subnormal value (exponent = 0 and mantissa with leading 0) $\to f = 2^{0} (\frac{d_1}{2}+\frac{d_2}{2^2}+\ldots+\frac{d_m}{2^m})\in [0,1)$ 值域不連續!
-
解決方法是 exponent = 0, 把 exponent +1, 也就是 x2 $\to f = 2^{1} (\frac{d_1}{2}+\frac{d_2}{2^2}+\ldots+\frac{d_m}{2^m})\in [0,2)$ 剛好和 exponent = 1 的 normal value 無縫接軌!
In summary, 浮點數可以用以下公式表示:
(Normal value, exponent > 0) $f = (-1)^s 2^{e-b} (1+\frac{d_1}{2}+\frac{d_2}{2^2}+\ldots+\frac{d_m}{2^m})\quad$ where $d_i \in {0, 1}$
(Subnormal value, exponent = 0) $f = (-1)^s 2^{1-b} (0+\frac{d_1}{2}+\frac{d_2}{2^2}+\ldots+\frac{d_m}{2^m})\quad$ where $d_i \in {0, 1}$
Biased exponent (最容易搞錯的地方):
- exponent (e) 的範圍:$ [0, 2^{exp\, bit}-1]$. 注意 exponent (value) 和 exponent bit(width) 不要混淆。
- Bias (b) 固定是 exponent 值域的中點-1:$2^{exp\,bit}/2-1 = 2^{exp\,bit-1}-1$
- 所以全部 (e-b) 的範圍: $[-2^{exp\, bit-1}+1,+2^{exp \,bit-1}]$
- 不過 exponent 的最小和最大值都被保為不同的用途:
- 最小值 (exponent = 0, i.e. all exponet bit = 0): 保留為 subnormal value, mantissa leading 1 變成 0.
- +/-0 是 subnormal (all exponent bit = 0) 的 speical case. 所有 mantissa bit = 0. Sign-bit 0 就是 +0, sign-bit 1 就是 -0.
- 最大值 (exponet = 1..1, i.e. all exponent bit = 1):保留為 +/-inf. Sign-bit 0 是 +inf, sign-bit 1 是 -inf.
-
所以 normal value (e-b) 範圍 $[-2^{exp\, bit-1}+2,+2^{exp \,bit-1}-1]$
-
(IEEE 754) FP16 exponent 是 5-bit, exponent 範圍: $[0,31]$, bias=15, 全部 (e-b) 範圍 [-15,+16], normal value (e-b) 範圍 [-14,+15].
- 最小值 $e=0 \to (e-b)=-15$ : subnormal value. 為了讓值域連續, e-b 加 1 : $f = (-1)^s \times 2^{-14} \times 0.\text{fraction}$
- 最大值 $e=31\to (e-b)=16$ : 保留給 +/-inf. +inf -> (s)0(e)11111(m)00..00; -inf -> (s)1(e)11111(m)00..00.
- $e \in [1,30] \to (e-b) \in [-14,+15]$ : normal value: $f = (-1)^s \times 2^{[-14,+15]} \times 1.\text{fraction}$.
- FP16 最大正值: $+2^{15}\times 1.11…11_2$. 最小 normal value 正值 $+2^{-14}\times 1.00…01_2$.
- FP16 mantissa 10-bit:
- 最大 normal value 值: $+2^{15}\times (2-2^{-10}) = 2^{16} - 2^{5} = 65536-32=65504 \sim 2^{16}$.
- 最小 normal value 正值 normal value: $+2^{-14}\times (1+2^{-10}) \sim 2^{-14}=6.1\times 10^{-5}$.
- 最小 subnormal 正值 $(-1)^s \times 2^{-15+1} \times 0.\text{fraction} = 2^{-14}\times 2^{-10}= 2^{-24} = 5.96\times 10^{-8}$.
-
FP32 exponent 是 8-bit, exponent (e) 範圍: $[0,255],$ bias (b) = $2^8/2-1=127$, (e-b) 範圍 $[-127, +128].$ normal value (e-b) 範圍 [-126,+127].
-
(e-b) 最小值 -127 (0-127) 是 subnormal value (包含 +/-0), 為了吸收 leading 1, e-b 再加 1 : $(-1)^s \times 2^{-127+1} \times 0.\text{fraction}$
-
(e-b) 最大值 +128 (255-127) 保留給 +/-inf. +inf -> 011…11; -inf -> 111…11.
-
(e-b) normal value: $(-1)^s \times 2^{[-126,+127]} \times 1.\text{fraction}$.
- Normal value 最大正值: $+2^{127}\times 1.11…11_2$. 最小正值 $+2^{-126}\times 1.00…01_2$.
- FP32 mantissa 23-bit:
- 最大 normal value 值: $+2^{127}\times (2-2^{-23}) \sim 2^{+128} =3.4\times 10^{+38}$.
- 最小 normal value 正值 normal value: $+2^{-126}\times (1+2^{-23}) \sim 2^{-126}=1.17\times 10^{-38}$.
- 最小 subnormal 正值 $(-1)^s \times 2^{-127+1} \times 0.\text{fraction} = 2^{-126}\times 2^{-23}= 2^{-149} = 1.4\times 10^{-45}$.
-
- 最小值 (exponent = 0, i.e. all exponet bit = 0): 保留為 subnormal value, mantissa leading 1 變成 0.

-
In summary: 如果 exponent is exp-bits (not e!!), mantissa is m-bits.
- 最大 normal value 值 = $2^{2^{(exp bit-1)}}- 2^{2^{(exp bit-1)}-m-1} \sim 2^{2^{(exp bit-1)}}$.
- Intuition: exponet 每多一個 bit, 最大值就平方倍增加!
-
最小 normal value 正值: $2^{-2^{(exp bit-1)}+2}+ 2^{-2^{(exp bit-1)}-m+2}\sim 2^{-2^{(exp bit-1)}+2}$.
-
最小 subnormal 正值 (>0): $2^{-2^{(exp bit-1)}+2} \times 2^{-m} = 2^{-2^{(exp bit-1)}-m+2}$
常見浮點數的動態範圍 (DR : Max, Normal Min, Subnormal Min)
-
FP32 的表示如下圖
- 1 sign-bit; 8 exponent-bit; 23 fraction-bit (mantissa).
- FP32 normal value 正值範圍: $[1.175 \times10^{-38}, 3.4 \times 10^{+38} (\sim 2^{128})]$, 負值範圍乘 (-1).

-
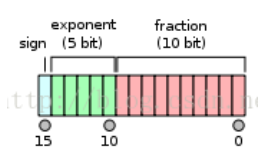
FP16 的表示如下圖:
- 1 sign-bit; 5 exponent-bit; 10 fraction-bit (mantissa).
- FP16 normal and subnormal value 正值範圍: $[5.96\times10^{-8}(\sim 2^{-24} ), 65504 (\sim2^{16})]$, 負值範圍乘 (-1).

-
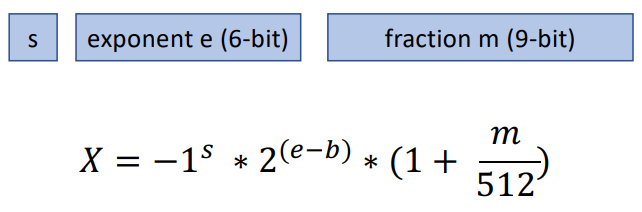
DLFloat16 (IBM) 如下圖: ARITH_ppt_final_AA (kyoto-u.ac.jp) [@agrawalDLFloat16b2019]
- 1 sign-bit; 6 exponent-bit; 9 fraction-bit (mantissa).
- DLF16 正值範圍: $[4.6\times10^{-10} (\sim 2^{?}), 8.59\times10^{+9}(\sim 2^{32})]$, 負值範圍乘 (-1).
- BF16 dynamic range 比起 FP16 大很多。 precision 差 6dB? 因爲 mantissa 少了 1-bit: 10-bit -> 9-bit!
- 從 FP16 轉 FP8 容易? 只要把 mantissa 直接砍 16-bit: 23-bit to 7-bit
-
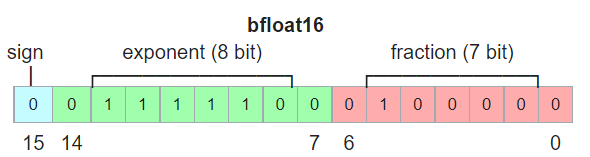
BF16 的表示如下圖:(直接 truncate FP32 的 faction from 23->7)
- 1 sign-bit; 8 exponent-bit; 7 fraction-bit (mantissa).
- BF16 正值範圍: $[1.17\times10^{-38}, 3.39\times10^{+38}]$, 負值範圍乘 (-1).
- BF16 dynamic range 非常大和 FP32 基本一致。但是 precision 並不好,因爲 mantissa 只有 7-bit!
- 從 FP32 轉 FP16 非常容易,只要把 mantissa 直接砍 16-bit: 23-bit to 7-bit
FP8 的表示如下圖:
- E5M2: 1 sign-bit; 5 exponent-bit; 2 fraction-bit (mantissa). Normal value (e-b) : [-14, +15]
- (Typical) E4M3: 1 sign-bit; 4 exponent-bit; 3 fraction-bit (mantissa). Normal value (e-b) : [-6, 7]
- (少用) E3M4: 1 sign-bit; 3 exponent-bit; 4 fraction-bit (mantissa). Normal value (e-b) : [-2, 3]
- (少用) E2M5: 1 sign-bit; 2 exponent-bit; 5 fraction-bit (mantissa). Normal value (e-b) : [0, 1]
- FP8 正值範圍: $[1.17\times10^{-38}, 3.39\times10^{+38}]$, 負值範圍乘 (-1).
- FP8 dynamic range 非常大和 FP32 基本一致。但是 precision 並不好,因爲 mantissa 只有 7-bit!
Intuition
我們可以用 log scale 數線增加 physical insight. 可以用鋼琴的鍵盤類比。
- 每一個 octave (8 度),對應一個 exponent-fixed bias value (e-b).
- Recall (e-b) total range: $[-2^{exp\, bit-1}+1,..,+2^{exp \,bit-1}]$. Normal value 的範圍 $[-2^{exp\, bit-1}+2,..,+2^{exp \,bit-1}-1]$, FP16 exp-bit = 5, normal value e-b = [-14, 15] 一共有 30 個 octaves.
- 88 鍵鋼琴一般有 7 個 octave.
- e-b = 0 對應 [1,2) 中央的 octave. 對應鋼琴的中央 C octave.
- 另外還有 subnormal value, 因為 leading 0, 所以從 0 開始包含無窮多個 octave, 相當於無窮多低音 octaves.
- 一般 bias b 是固定在中間,所以左右對稱。在 FP8 情況下,bias 可以調整。調整 bias 的 intuition 就是移動中央 octave 的位置。b 每增加 1, 所有 octave 左移一個 octave. 所有值 / 2,當然最大值也除 2, 增加 overflow 的機會。相反 b 每減少 1,所有 octave 右移動。所有值乘 2. 為什麼 FP8 需要調整 bias? 因為 FP8 的 dynamic range (從最小到最大值) 有限。只能靠 bias 把 octave 移到 data 的範圍,處理完後在移回原來的範圍。
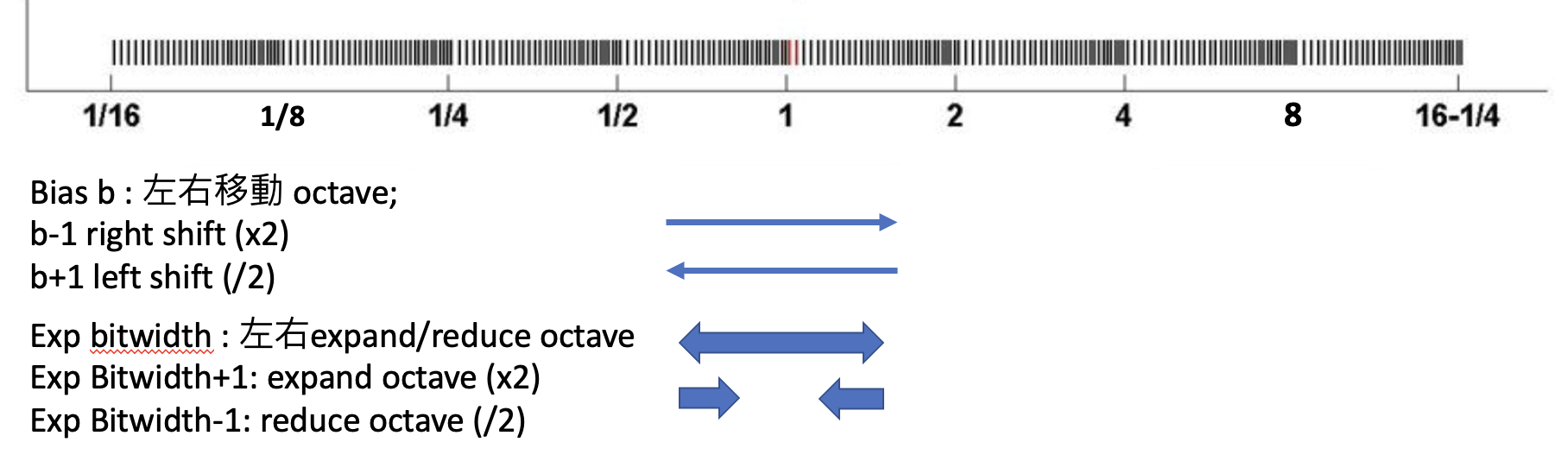
- Exponent bit, 不是 exponent value. Exponent bit 每增加 1-bit, 就會 expand octaves (both 最大和最小) 兩倍。就是變成兩倍 octaves! 相反 exponent 每減少 1-bit, 就會把 octave 減半。注意 octave 是 log-scale. 所以兩倍的 octaves 代表 dynamic range 平方。例如 FP16 的 exponent bit 是 5-bit: normal value 最大值是 $\sim 2^{16}=65536$, 最小值是 $\sim 2^{-14}$. 如果變成 6-bit, normal value 最大值 $\sim 2^{32}=(65536)^2$, 最小值是 $\sim 2^{-30}$. 當然代價是 mantissa 就變少 1-bit, 因此 precision 會降低。
- Mantissa 就是在 1 個 octave 要均勻 (linear scale) 切幾份。注意在 log-scale 的 linear scale 看起來就像上圖非均勻。用鋼琴的類比就是琴鍵的數目。鋼琴 1 個 octave 有 10 (黑白) 鍵。這裡有 $2^{mantissa-bit}$ keys. 如果只看一個 octave, 每增加一個 mantissa bit, quantization noise 減少 6dB. 每減少一個 mantissa bit, quantization noise 增加 6dB. 不過一般 input signal 很少是在一個 octave, 所以 quantization noise 似乎不是這麼直接。和 input signal 強相關。我們後面討論。
- Trade-off between dynamic range and precision: 因為 total bitwidth 是固定的。例如 FP16 只有 15-bit exclude sign-bit. 增加 exponent bitwidth 對於 dynamic range (octave x2, 最大和最小值基本平方) 非常有幫助。但是對於 precision.
如何評估浮點數的動態範圍 (DR) 和精準度 (Precision)?
精準度和 input signal 強相關,因此最好的判斷是用 SNR. 同時看 signal and quantization noise.
- (Random) Sine wave
-
假設 sine wave 頻率 f Hz, 振幅 A:
$x = A \sin(2 \pi f t_n + 2\pi\theta)$ where $tn \in [0,1)$ 均勻等分不含 endpoint; $\theta \in [0,1]$ 是 uniform random variable.
-
$x$ 是 zero-mean, $A = \sqrt{2}\text{ RMS}$
-
Spatial distribution: (not uniform, 接近 +/-A 最大,0 最小):
- $50\% \in [-\sigma, +\sigma]$, $100\% \in [-1.41\sigma, +1.41\sigma]$
-
Deterministic sine wave 就是把 $\theta = 0$, 廣泛用於 ADC SNR 分析. 不過我們這裡用 sine wave with random phase (uniform distribution) 避免永遠 sample 在特定的 waveform points.
-
Frequency domain power spectrum: Lorentian, 如果 $\theta = 0$ 就變成一個 delta function.
-
-
Uniform distribution : random signal without outlier.
$x = u(-A,+A)$ $u \in [-A,A]$ 是 uniform random variable.
- $x$ 是 zero-mean, $A = \sqrt{3}\text{ RMS}$
- Spatial distribution: (uniform, 從 -A to +A 都一樣 “uniform”): ? samples in $1\sigma$, 100% samples in $1.73 \sigma$.
- $58\% \in [-\sigma, +\sigma]$, $100\% \in [-1.73\sigma, +1.73\sigma]$
- Frequency domain power spectrum: white.
- Norma distribution: most common random signal, the tail decay very quick.
- $x = N(m,\sigma)$ $N$ 是 uniform random variable.
- $x$ 一般設為 zero-mean (m=0).
- Spatial distribution: (not uniform, 接近 0 最大,bell shape but never zero):
- $68\% \in [-\sigma, +\sigma]$, $95\% \in [-2\sigma, +2\sigma]$, $99.7\% \in [-3\sigma, +3\sigma]$
- Frequency domain power spectrum: white
動態範圍 包含最大值和最小值。我們先看最大值。
最大值: overflow
最小值: between the normal value minimum and subnormal value minimum, defined by SNR!!!! (e.g. 20 or 40dB, or 1/2 of SNR_max!)
Precision: defined by SNR!
Fixed-Point SNR Review
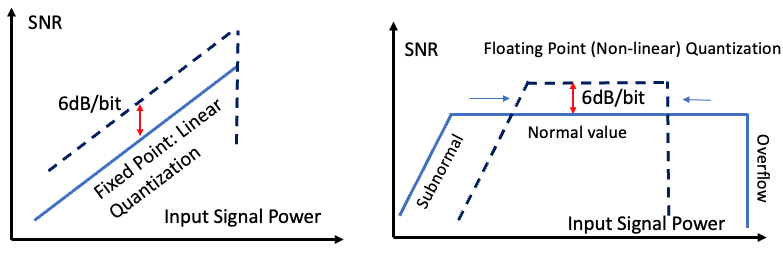
對於 fixed-point linear quantization, dynamic range 和 quantization 的 trade-off 是 well-known, 如下圖。
首先 signal-to-quantization noise (SNR) 和 input signal power (RMS: Root-Mean-Square in dB) 成正比。
因為 quantization noise 基本是定值,所以信號愈大,SNR 就愈好,一直到 full scale (overflow).
對於 sine signal, $SNR_{max} = 6\times bitwidth + 2$ dB. 例如 INT8 最大 SNR 是 50dB, INT10 SNR(max) = 62dB.
- 每增加一個 bit, SNR 增加 6dB.
-
Full-scale $SNR_{max} \approx 6\times bitwidth + 2$ dB
-
如果 input signal 沒有充分利用 dynamic range, SNR 就會變小。
- 這是 fixed point 最大的挑戰。如何 fully loaded dynamic range.

Floating-Point SNR
我們先用簡單的例子 uniform distribution 得到一些 physical insight.
-
假設 input signal 剛好是在一個 octave 內, e.g. [1,2]. 因為 within a octave 基本就是 linear quantiztion, SNR 的結果就和 fixed-point 一樣,$SNR_{max} = 6 \times \text{mantissa-bit} + 2$ dB. 不過實務上不可能,也浪費了 exponent bits.
- 比較實際的 input signal uniform distributed between [-1, 1]. 因為正負左右對稱,只要看 [0, 1] 即可。這個範圍包含無窮多 octaves.
- 假設有 N 個 samples uniformly distributed [0, 1],一半 (N/2) samples 會落在 [1/2,1] octave, 另一半落在 [0, 1/2] (無窮多 octave)。 繼續推導可以得到: N/2 samples in [1/2,1], N/4 samples in [1/4,1/2], N/8 samples in [1/8,1/4], …. 就是越靠近 0 的 octaves 分到的 samples 越少。但是每一個 octave 的 SNR 都一樣!因此 ideally 平均的 SNR 就和一個 octave 的 SNR 一樣!
- 這是非常奇妙的結果:(1) $SNR_{avg} = 6\times \text{mantissa-bit} + 2$ dB (No! uniform distribution 需要修正),還是 mantissa bitwidth 決定 SNR_avg; (2) 更重要的是這個 SNR_avg 和 input signal 的 power 無關! 只要 input signal power 是在 normal value 的 octave 範圍。當然如果 input signal power 比 normal value 小,進入 subnormal range, SNR 就會下降。
- 簡單來說,floating point 就是把 fixed point 的一些 mantissa-bits 轉成 exponent-bits: 好處是增加 dynamic range 以及讓小信號的 SNR 變好。 第二點對於 normal distribution signal 很重要,因為大部分信號都是小信號。壞處是 $SNR_{max}$ 變小。
- 所以 floating point 的挑戰就是 best fit signal dynamic range and distribution.
- max octave 必須大到讓信號不產生 overflow. 方法是 (a) 調整 exponent bitwidth (at the expense of SNR); (b) 調整 bias b (right shift, FP8 就是用這個方法。不過要小心 underflow)
- Floating point SNR 和 signal distribution 無關; fixed point SNR 和 signal distrution 相關! Floating point SNR > Fixed point SNR when signal is small. 反之 fixed-point SNR > floating point SNR when signal is large.
Simulation for Dynamic Range and Precision
我們先定義 Lp norm 以及 Lp-mean:
\(\| x\|_p=\left(\sum_i^n |x_i|^p\right)^{1 / p} \,\, (L_p\text{ norm}) \longrightarrow \|x\|_{p-mean}=\left(\frac{1}{n}\sum_i^n\left|x_i\right|^p\right)^{1 / p} \,\, (L_p\text{ mean})\)
L2 norm 代表 Euclidean distance to 原點。另一個常用 metric 是 RMS (Root-Mean-Square). 物理上代表 power (i.e. rms voltage); 統計上代表 standard deviation (std) 不過要假設 zero-mean.
\(\|x\|_2=\sqrt{\sum_i^n x_i^2}=\sqrt{x_1^2+x_2^2+\ldots+x_n^2} \,\, (L_2\text{ norm}) \longrightarrow \|x\|_2=\sqrt{\frac{1}{n}\sum_i^n x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\ldots+x_n^2}{n}} \text{ (RMS)}\)
L1 norm 代表 taxicab distance to 原點。L1 norm 的平均稱為 absolute mean.
\(\| x\|_1=\sum_i^n |x_i|=|x_1|+|x_2|+\ldots+|x_n| \,\, (L_1\text{ norm}) \longrightarrow \|x\|_1=\sqrt{\frac{1}{n}\sum_i^n |x_i|}=\sqrt{\frac{|x_1|+|x_2|+\ldots+|x_n|}{n}} \text{ (abs. mean)}\)
https://tex.stackexchange.com/questions/416450/the-formula-alignment-across-a-table-column
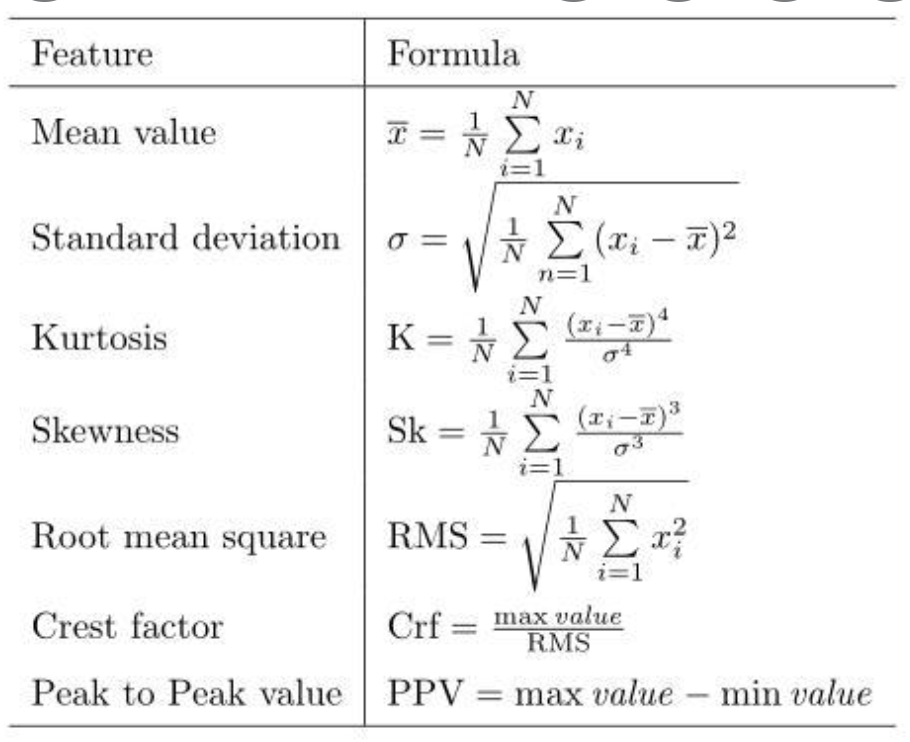
\(\text{Mean value} & \overline{x}=\frac{1}{n}\sum_{i=1}^{n}x_i \\
\text{Standard deviation} & \sigma = \sqrt{\frac{1}{n}\sum_{n=1}^{n}(x_i - \overline{x})^2} \\
\text{Kurtosis} & \text{K}=\frac{1}{n}\sum_{i=1}^{n}\frac{(x_i-\overline{x})^4}{\sigma^4} \\
\text{Skewness} & \text{Sk} = \frac{1}{n}\sum_{i=1}^{n}\frac{(x_i-\overline{x})^3}{\sigma^3} \\
\text{Root mean square} & \text{RMS} = \sqrt{\frac{1}{n}\sum_{i=1}^{n}x_i^{2}} \\
\text{Crest factor} & \text{Crf} = \frac{\max \text{value}}{\text{RMS}} \\
\text{Peak to Peak value} & \text{PPV} = \max \text{value} - \min \text{value}\)
如果不是 zero-mean, 容易證明 $\sigma^2 = \text{RMS}^2 - \overline{x}^2 $
用絕對值平均 (absolute mean, 就是 L1 norm/n) 做為 Baseline
為什麼用絕對值平均?因為最簡單,只有加法和平均。絕對值是避免 quantization error 被平均掉。
Dynamic Range
先看 uniform distribution 的 dynamic range
- SNR is constant
- SNR is indepednent of distribution (uniform and normal)
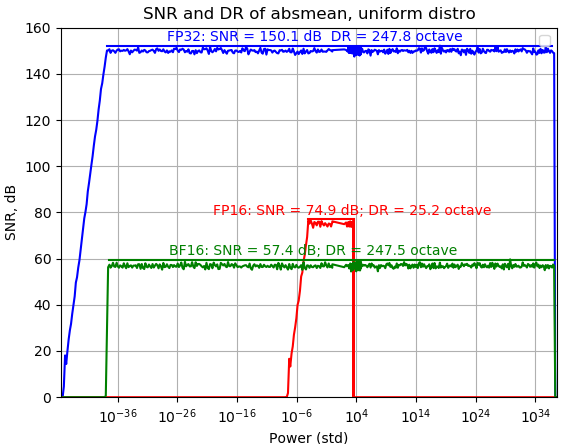
Uniform Distribution Dynamic Range Vs. SNR

FP32: $\min =4.2\times 10^{-39}$; $\max = 1.45\times 10^{37} \Rightarrow \log(\max/\min) / \log2 = 251$ octaves.
- normal value (e-b) 範圍 [-126,+127] -> 254 octaves, 差了 3 個 octave, 可能是 vec_len = 16.
BF16: $\min =2.7\times 10^{-38}$; $\max = 1.45\times 10^{37} \Rightarrow \log(\max/\min) / \log2 = 248$ octaves.
FP16: $\min = 3.6\times 10^{-5}$; $\max = 3\times 10^{3} \Rightarrow \log(\max/\min) / \log2 = 26.4$ octaves.
Use automatic script.
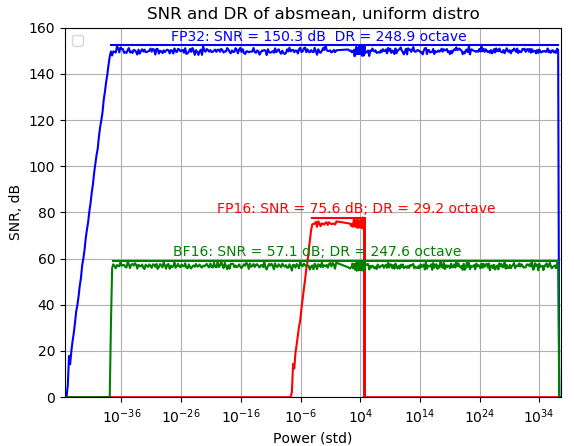
FP16 Internal accumulation changed to FP32.
-
FP16 DR increases to 29.2 octave, +4 octaves!
-
SNR 基本沒變化
Normal distribution with internal 16-bit (with vec_len=16)
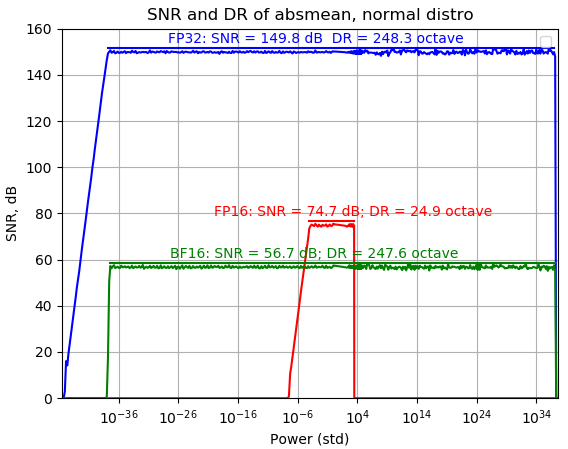
FP16 Internal accumulation changed to FP32.
FP16 DR increases to 28.5 octave, +3.6 octaves!
SNR 似乎好了一點。
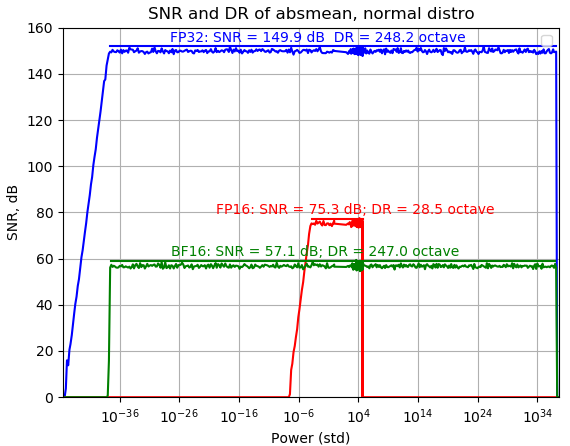
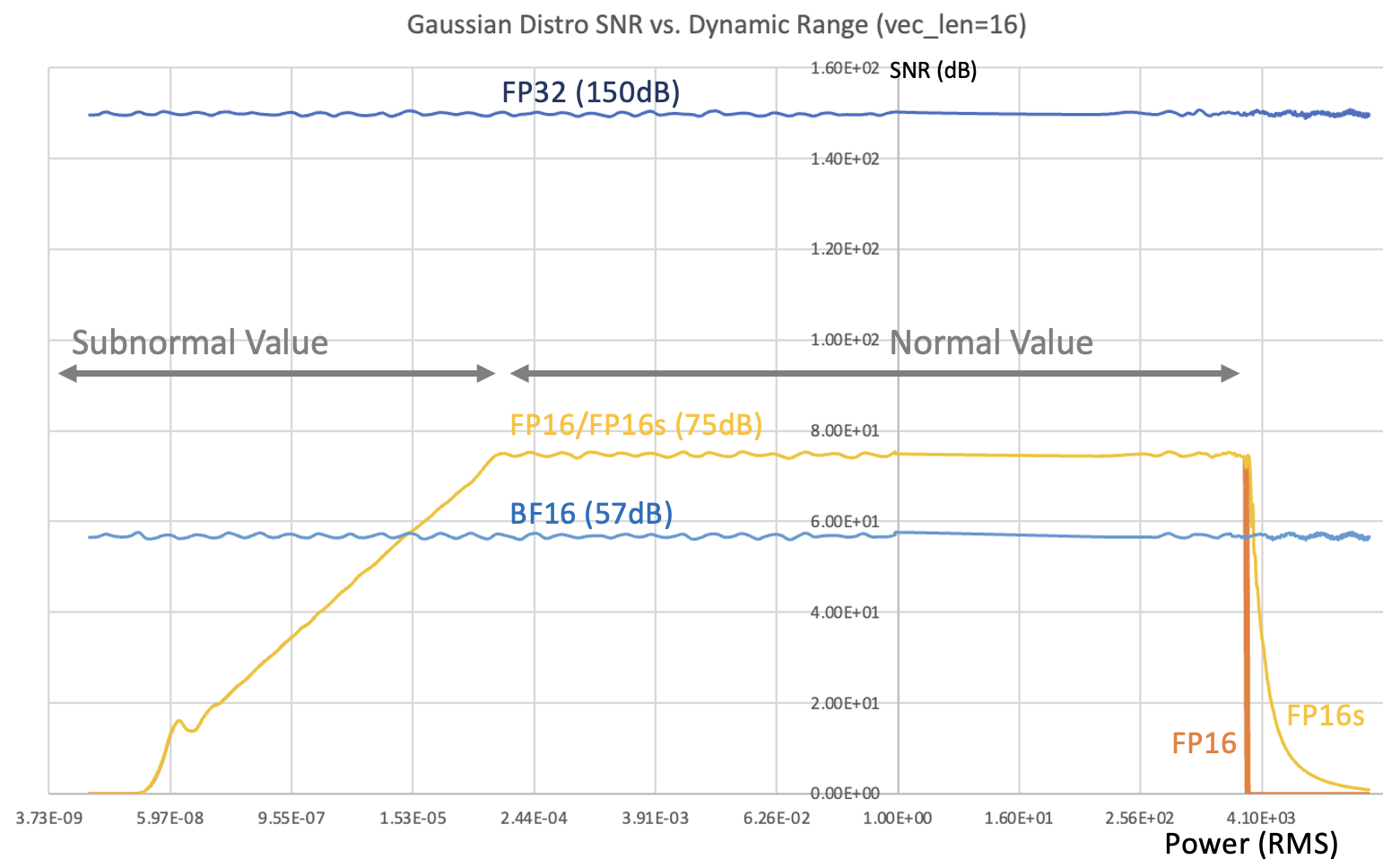
Zoom-In to 16-bit (FP16/FP16s/BF16)
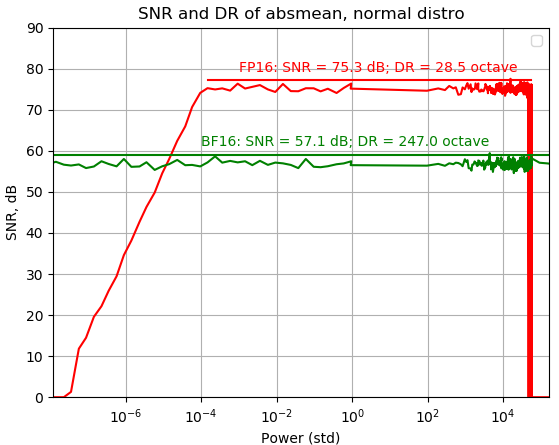
FP16s is using internal FP16, so the DR range is smaller!
Change to internal FP32
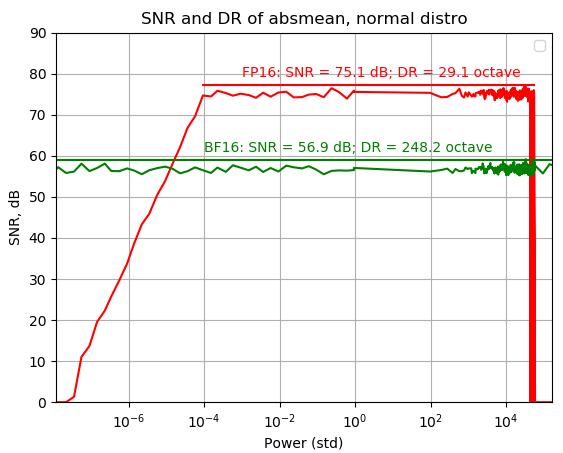
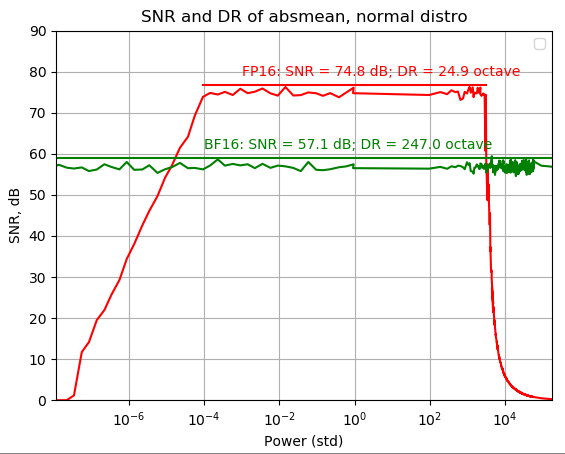
FP16s 基本沒有增加什麼 dynamic range, 因為 SNR 掉的很快。
注意每一格是 x16, 也就是 4 octaves. FP16 normal value 包含 6.x 格,也就是 6.x x 4 = 26 octaves.
- FP16 的 normal value (e-b) 範圍 [-14,+15], 應該有 30 octaves. 主要原因是 vector length = 16 and accumulator FP16, 有 4 個 octaves 在 maximum value 被犧牲,之後要 check. 還有和 distribution 有關。
- FP32 和 BF16 (exponent 8-bit) 都會在兩邊 8 倍 octaves (16x8=128). normal value (e-b) 範圍 [-126,+127]
- FP16 比起 BF16 的 SNR 增加 18dB (3-mantissa bit).
- FP32 比起 FP16 的 SNR 多了 75dB (23-bit - 10-bit = 13-bits around 78dB), 少了 3dB 可能是 error accumulation.
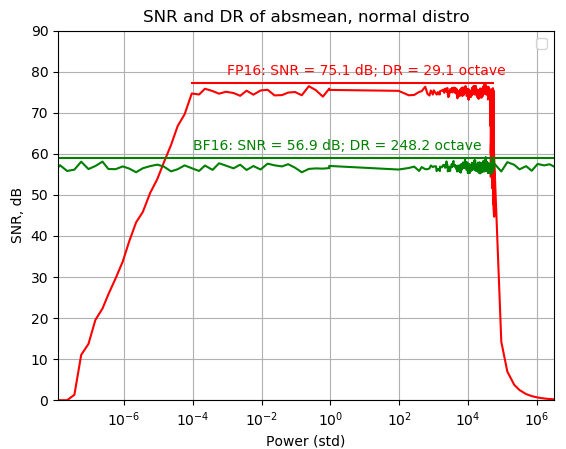
Use 10x decade.
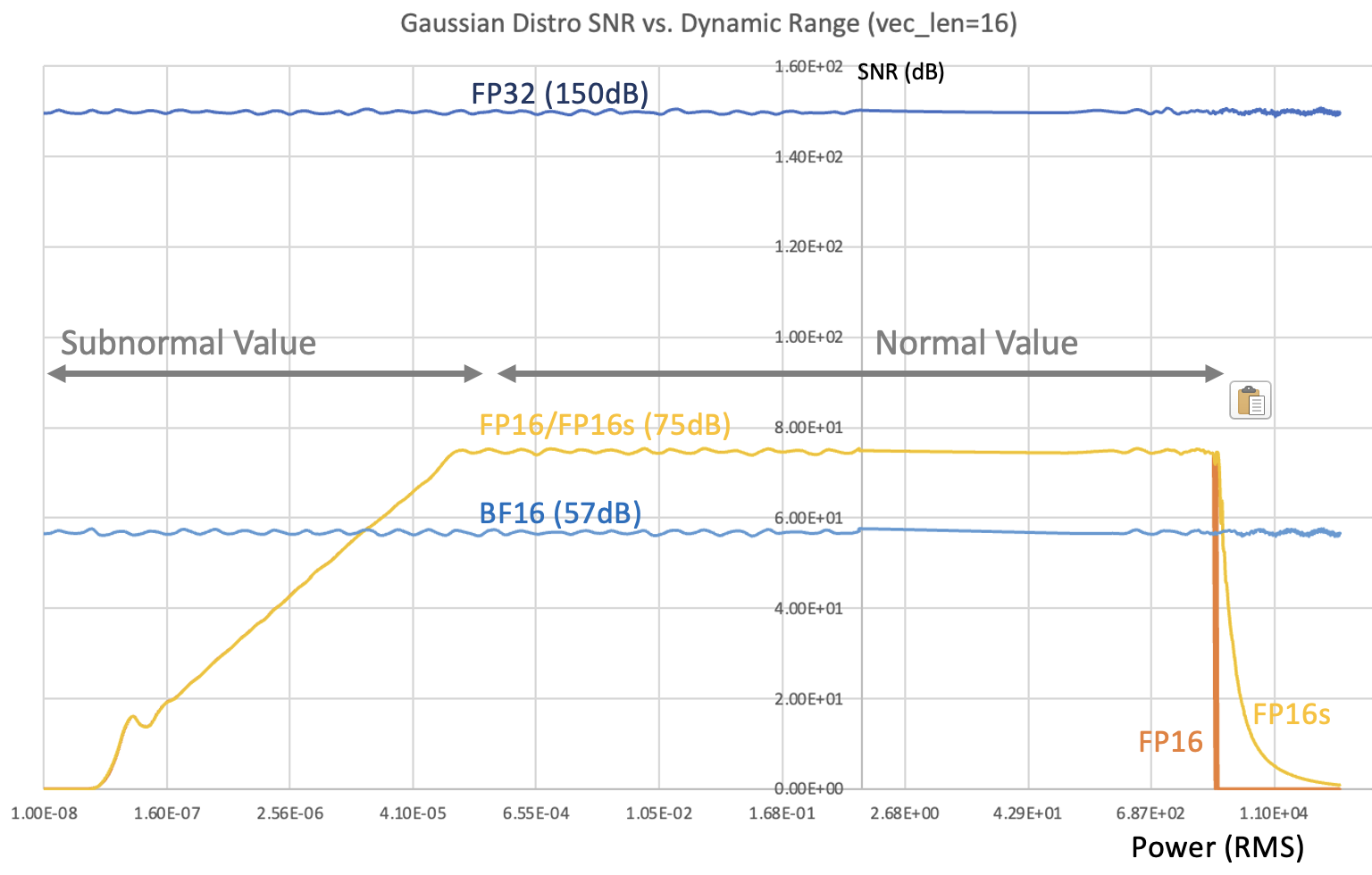
(RMS, 就是 L2 norm/sqrt(n) 做為 Comparison, 16-bit internal
Uniform, internal precision fp16, threshold 40, vec_len=16
FP16s2seg 比起 FP16 多了8.5 octaves! but SNR drops!
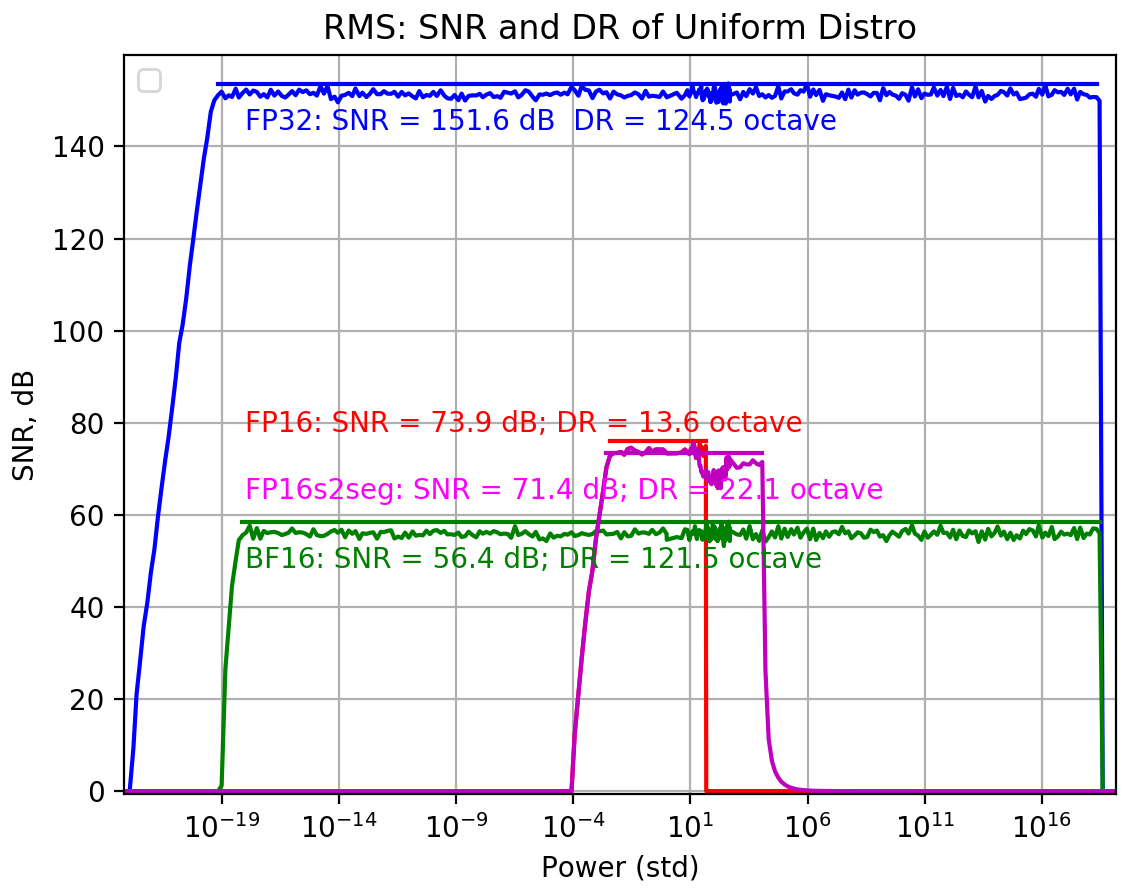
Internal precison 改成 fp32 (only fp16!):
Uniform, internal precision fp32, threshold 40, vec_len=16
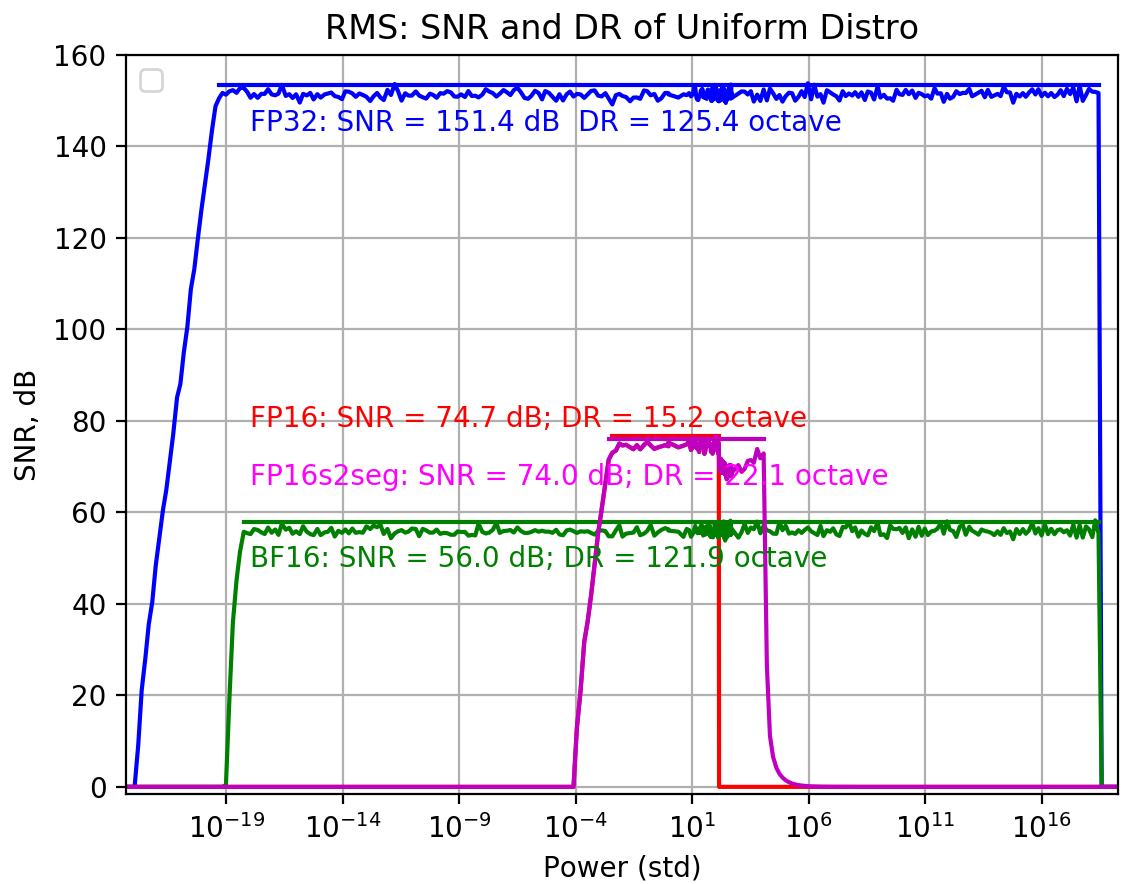
FP16 多了0.9 octaves. 但是 FP16s2seg 沒有改變, why? to be checked! (because it’s already become lapack rms!)
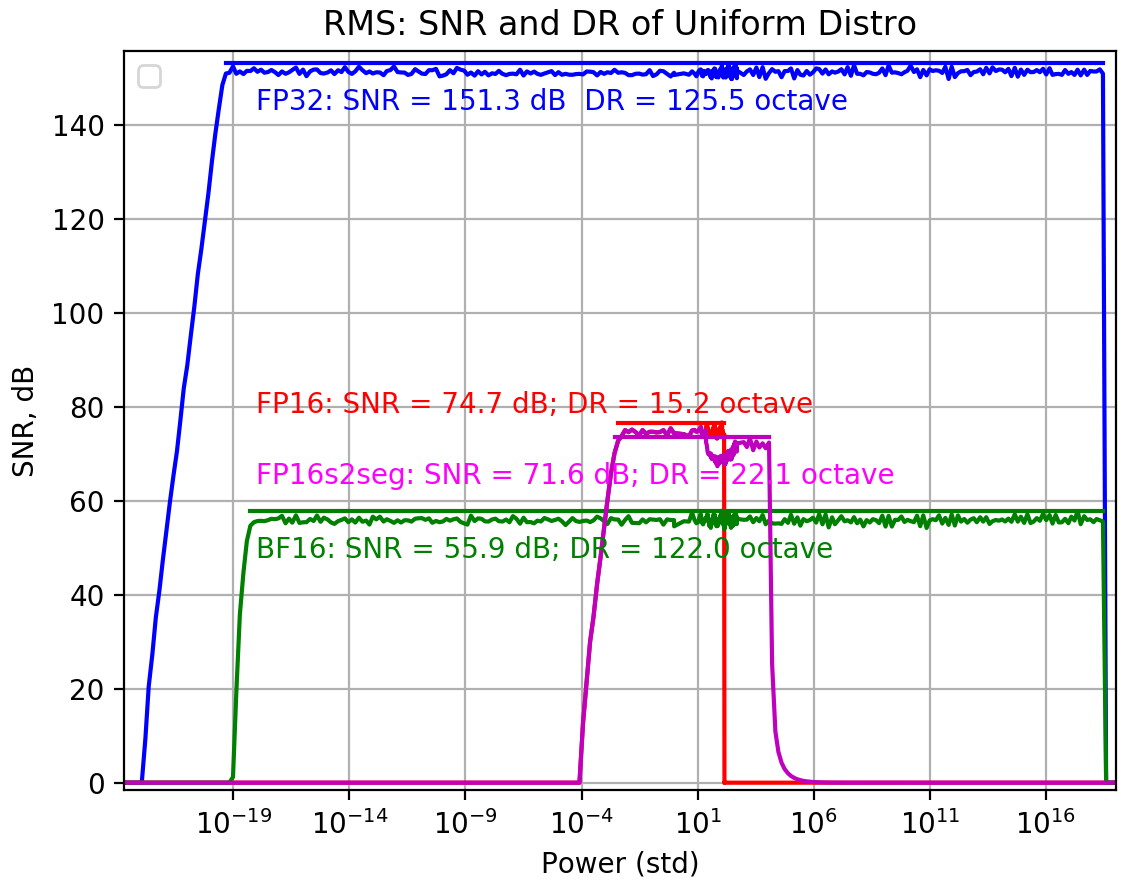
Uniform, internal precision fp32, threshold 250!, vec_len=16
Normal Distribution
internal precision fp16, threshold 40, vec_len=16
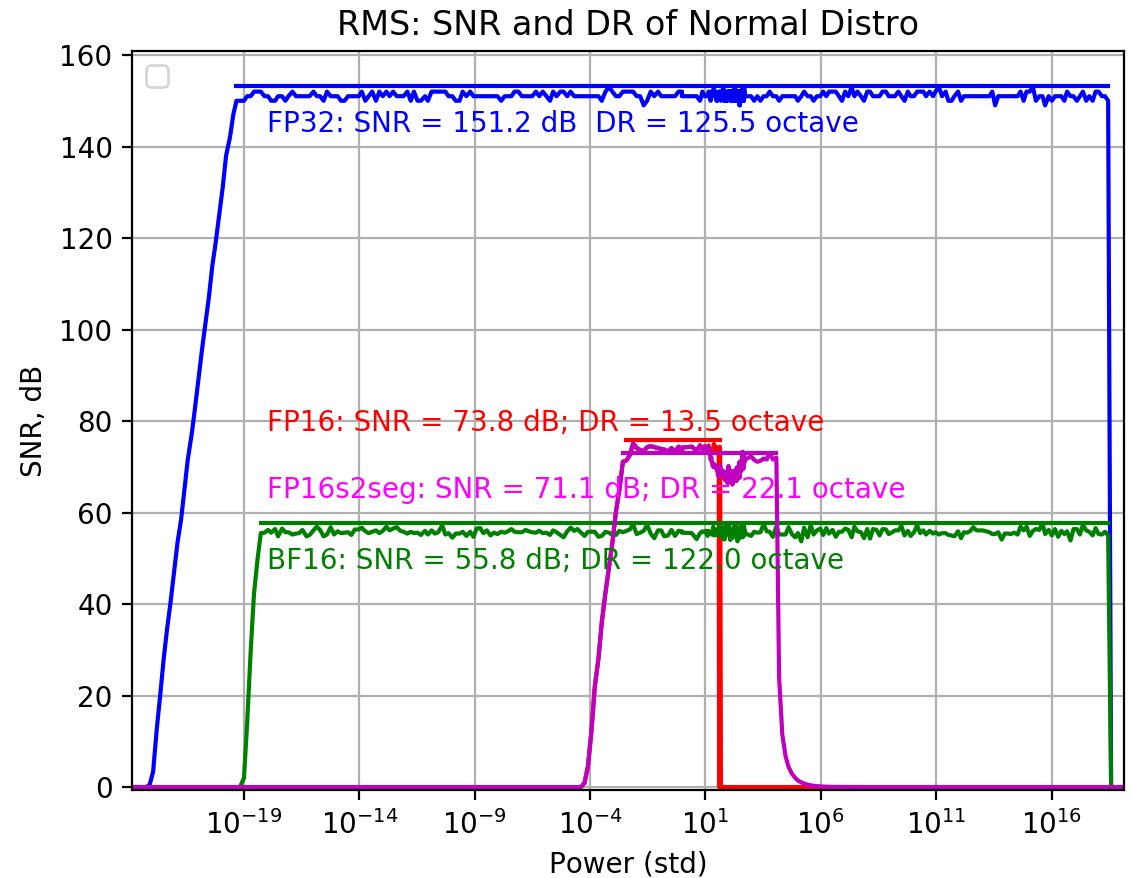
internal precision fp32, threshold 40, vec_len=16
Internal precison 改成 fp32:
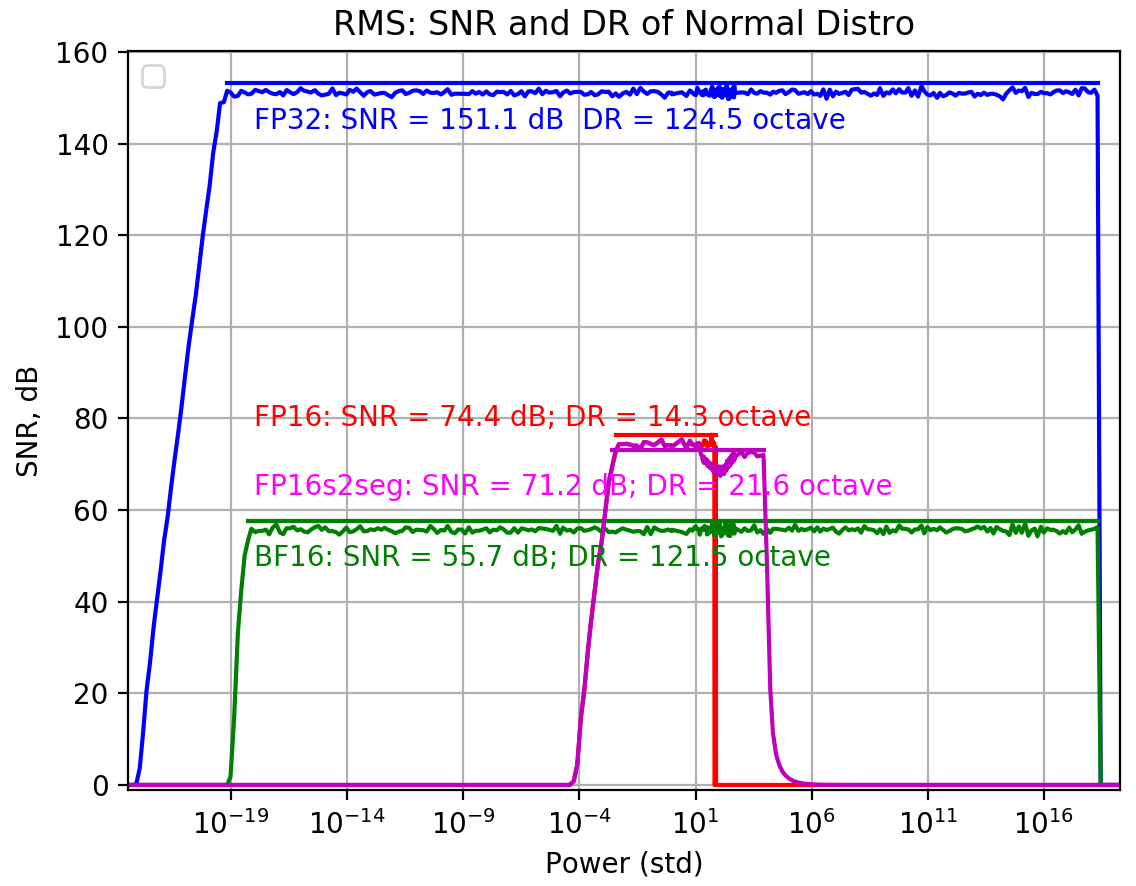
internal precision fp32, threshold 250, vec_len=16
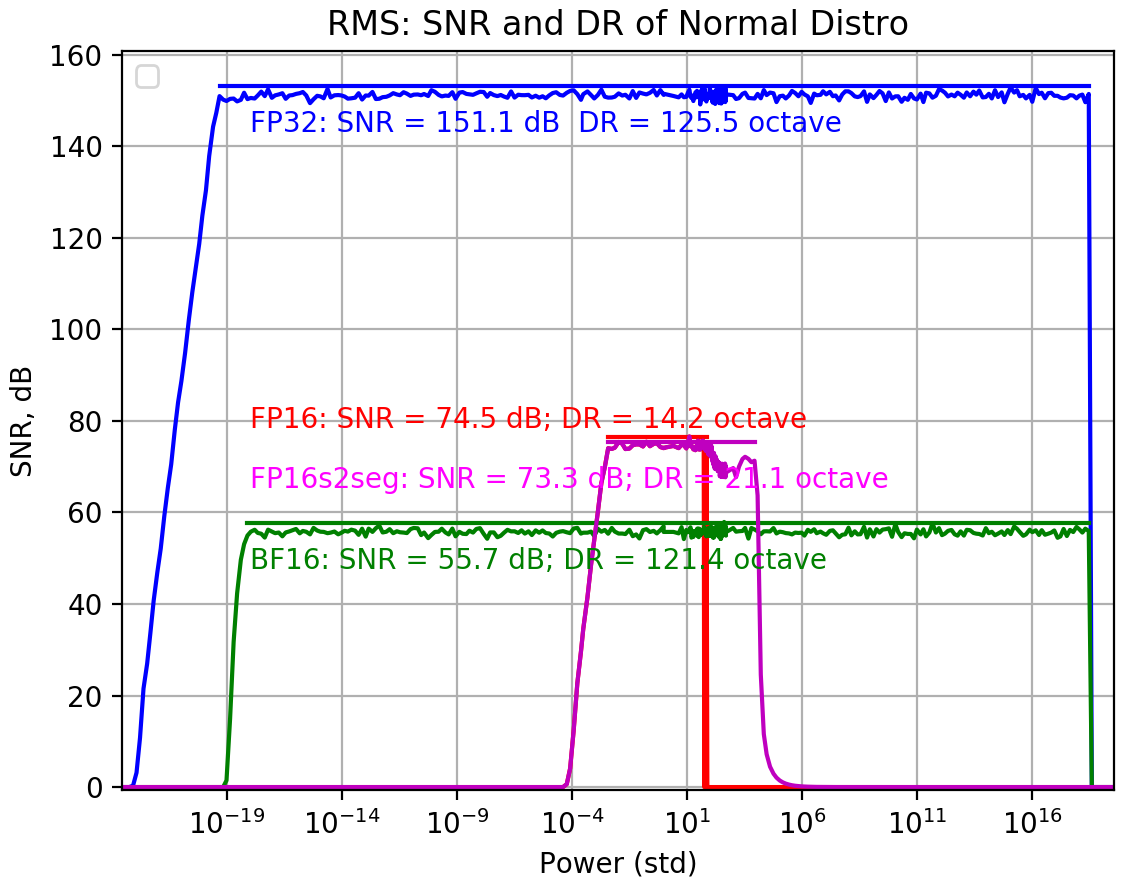
非常有趣是加上 Lapack 方式做為比較。 Lapack 的方法就 dynamic range 更好,但是 SNR 變小。
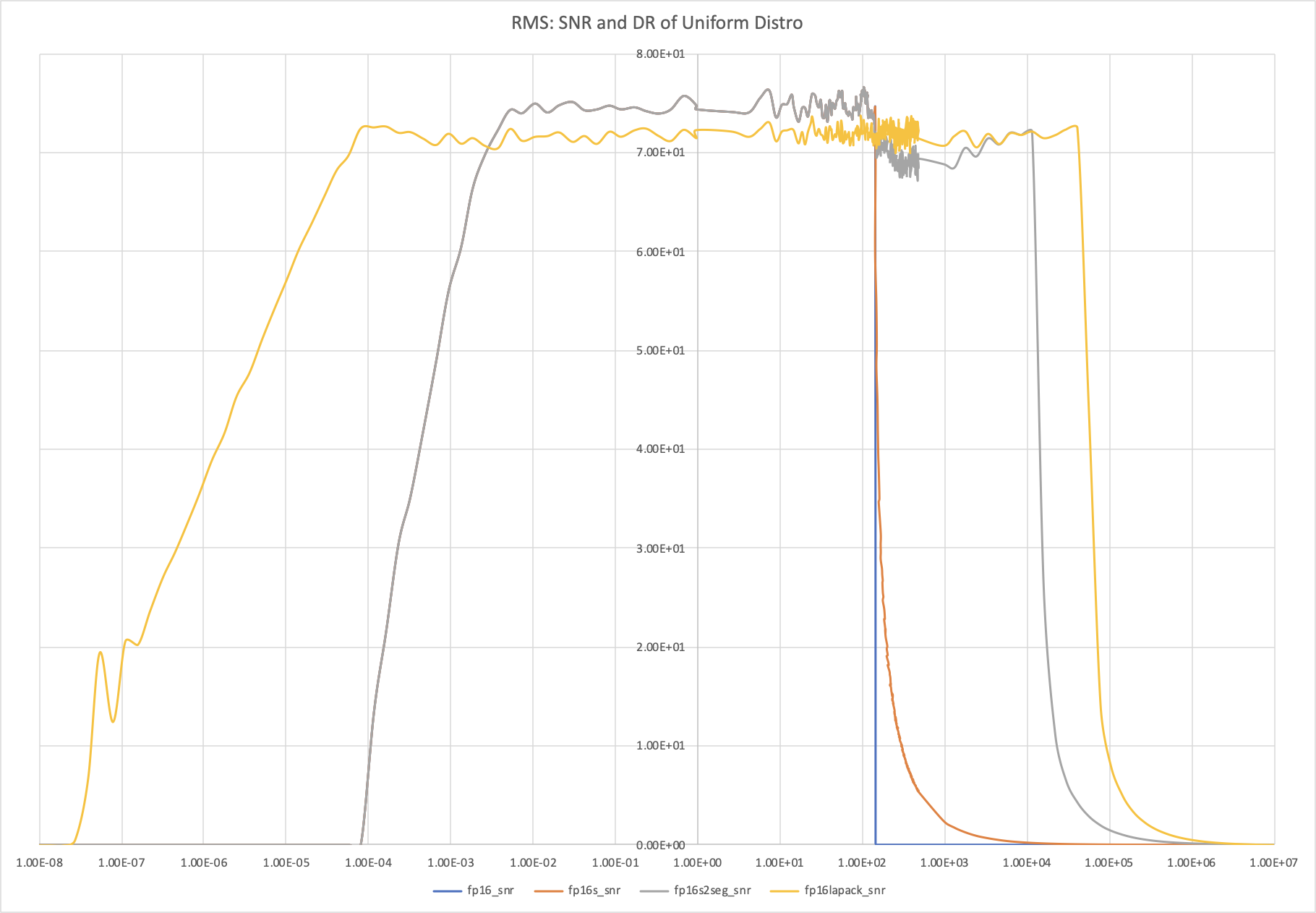


-
[] :左右都 close. ():左右都 open. [) 左 close, 右 open. ↩