Information Theory - Constrained Noiseless Channel Capacity

Posted on | In

Major Reference and Summary

book.pdf (inference.org.uk) Chap 17, from MacKay 是經典 information theory textbook.

重點

  • Noisy channel capacity with (memory) constraint $C = \lim_{n\to\infty} \max_X \frac{1}{n} I(X^n;Y^n) = \lim_{n\to\infty} \max_{X^n} \frac{1}{n} (H(X^n) - H(X^n Y^n))$.
    • 此處 $p(X^n) = p(x_1, x_2, …, x_n)$. 同樣 $p(Y^n) = p(y_1, y_2, …, y_n)$
  • Noiseless channel capacity with (memory) constraint $C = \lim_{n\to\infty} \max_X \frac{1}{n} I(X^n;Y^n) = \lim_{n\to\infty} \max_{X^n} \frac{1}{n} H(X^n)$.
  • Noisy channel capacity without memory $C = \lim_{n\to\infty} \max_X \frac{1}{n} I(X^n;Y^n) = \max_{X} (H(X) - H(X Y))$.
    • 此處 $p(X^n) = p(x_1, x_2, …, x_n)=p(x)^n$. 同樣 $p(Y^n) = p(y_1, y_2, …, y_n)=p(y)^n$
    • 可以證明 $H(X^n)=n H(X)$, $H(X^n Y^n) = n H(X Y)$, $I(X^n;Y^n)=n I(X;Y)$
  • Noiseless source capacity without memory: $H(X)$.
  • 低於 capacity, 理論上存在 code 可以達到 error free compression/communication!

Information Theory Applications

Shannon 的信息論 (Information Theory) 可以應用到 contrained channel。常見於 storage channel, 例如磁性材料用於硬碟 (partial response channel)，bandwidth limited communication channel, 或是為了 receiver clock recovery 而引入的 constrains (e.g. 4B5B or 8B10B encoding).

下表比較 source, noisy channel, constrained channel 的差異。

Information Source Noisy Channel Noiseless Constrained Channel
Application Compression Communication Storage
Source/Channel
Capacity		 Source entropy: $H(X)$ Max source/receiver
mutual-info: $\max I(X;Y)$		 Max source sequence entropy: $\lim_n \max H(X^n)/n$
Shannon Theory Source Coding Theorem Channel Coding Theorem Source coding + state/trellis diagram

前文聚焦在 noisy channel coding theory，本文聚焦在 noiseless channel 的 capacity. 當然硬碟或是 bandwidth limited channel 還是會有 noise. 實際的應用會是 noisy + constrained channel. 為了簡化，本文主要討論 noiseless constrained channel (r = t).

image-20230124162151769

Constrained Binary Channels

Channel A - 禁止 substring 11

  • 所有 1 後面至少要有一個 0, 但是 0 沒有任何限制。Valid string: 00100101001010100010.
  • 理由：有些 transmitter 在傳輸 ‘1’ pulse 需要 1 clock cycle 的恢復時間。
  • 舉例 s = 0010,1101,1100,1 $\to$ r = 0010,0101,0010,1010,0010 $\to$ s’ = 0010,1101,11001
    • 簡單 check: transmission rate: R = 13/20 = 0.65-bit
    • 假設 50% ‘1’ 和 50% ‘0’. ‘1’ -> ‘10’; ‘0’ ->’0’, 所以 transmission rate: R = 2/3 = 0.66-bit
  • 如果都傳輸 0, transmission rate = 1-bit? No, 只傳輸 0, 雖然有 channel capacity, 但是無法 encode 任何 information, i.e. $H(X^n) = 0$.
  • Question: channel capacity $C \ge R$. $C$ 會比 0.66-bit 更大嗎?

Channel B - 禁止 substring 101 and 010

  • 所有 1 或 0 都要 group of two or more. Valid string: 0011100111001100001.
  • 理由：磁性材料如果是單獨的 island (010 or 101) 會不穩定。所以需要 in group.
  • 舉例：50% ‘1’ 和 50% ‘0’. ‘1’ -> ‘11’; ‘0’ ->’00’. Transmission rate: R = 1/2 = 0.5-bit
  • Question: channel capacity $C \ge R$. $C$ 會比 0.5-bit 更大嗎? Yes!

Channel C - 禁止 substring 111 and 000

  • 所有連續的 1 或 0 最大 runlength 為 2. Valid string: 10010011011001101001
  • 理由：太長的 1 或 0 runlength 會造成 clock recovery 不準確
  • 舉例：50% ‘1’ 和 50% ‘0’. ‘1’ -> ‘10’; ‘0’ ->’01’. 可以證明最大 runlength 為 2, 稱為 Manchester encode for clock recovery. Transmission rate: R = 1/2 = 0.5-bit
  • Question: channel capacity $C \ge R$. $C$ 會比 0.5-bit 更大嗎?

以上三種 channels 都可以歸類於 runlength limit channels 如下：

image-20230125181530099

是否有更系統的方法找出 noiseless constrained channel capacity?

Channel Capacity With Constraint

先看 general case: noisy + constrained channel

  • Noisy constrained channel: 因為 constrains, symbol (temporal) 之間有 dependency，也就是 memory.

    • Input/output $X^n,Y^n$ 之間的 mutual information: $I(X^n; Y^n) = H(X^n) - H(X^n Y^n)$

      • 此處 $p(X^n) = p(x_1, x_2, …, x_n)$. 同樣 $p(Y^n) = p(y_1, y_2, …, y_n)$

      • $H(X^n) = - \sum_i p(X^n) \log_2 p(X^n)$, $i$ 一共有 $2^n$ sequences.

    • $I(X^n; Y^n) \ne n (I(X;Y))$ and $H(X^n) - H(X^n Y^n) \ne n H(X) - nH(X Y)$
    • Constrained channel capacity 不能僅看一個 symbol 的 mutual information, 要看 $n$-symbol 的平均值: $C = \lim_{n\to\infty} \frac{1}{n} \max_X I(X^n;Y^n) = \lim_{n\to\infty} \max_{X^n} \frac{1}{n}(H(X^n) - H(X^n Y^n))$.
  • Noisy memoryless channel: symbol (temporal) 之間都是獨立事件。
    • Input/output $X,Y$ 之間的 mutual information: $I(X;Y)=H(X)-H(X Y)$.
    • Memoryless: $I(X^n; Y^n)= n I(X;Y) = H(X^n) - H(X^n Y^n)= n(H(X)-H(X Y))$.

    • Channel capacity (normalized to 1-symbol), C = maximum mutual information, $C = \max_{X^n} \frac{1}{n} I(X^n;Y^n) = \max_X I(X;Y)$.

    • Memoryless channel capacity 只要看一個 input / output symbols 的最大 mutual information (entropy-conditional entropy) 即可。
  • Noiselss constrained channel: 因為 output symbol 完全 dependent on input symbol (spatial)! Mutual information 等於 source entropy.
    • $H(X^n Y^n)=0 \to I(X^n;Y^n)=H(X^n)$ 所以 mutual information 就是 source entropy.
    • Noiseless channel capacity, $C = \lim_{n\to\infty} \frac{1}{n} \max_{X^n} H(X^n)$ 當然此處的 $X^n$ under constraints, 所以 $H(X^n) \ne n H(X)$.

In summary, Noiseless constrained channel capacity, $C = \lim_{n\to\infty} \max_{X^n} \frac{1}{n} H(X^n)$

Noiseless Constraint State Diagram and Matrix

Use State diagram, Trellis diagram, adjacent matrix of directed graph 計算 channel capacity.

Caveat: adjacent matrix of directed graph 不等於 transition matrix!

  • Transition matrix 包含 transition probability. 每一列 (row) 的和為 1. 最大的 eigenvalue 為 1 (Perron-Frobenius theorem).
  • adjacent matrix of directed graph 只是表示 state diagram 的連結，沒有包含 transition probability 的觀念。最大的 eigenvalue is bounded by degree of the connection (一個 node 最多的 connections). 如果用 Perron-Frobenius theorem, 就是介於最大和最小的 row sum 之間。不考慮 isolated nodes (no input/output), 最大的 eigenvalue > 1.
  • 還是 transitional probability 是我們最後要 optimize 的結果 for maximum entropy?

下圖包含 Channel A, B, C.

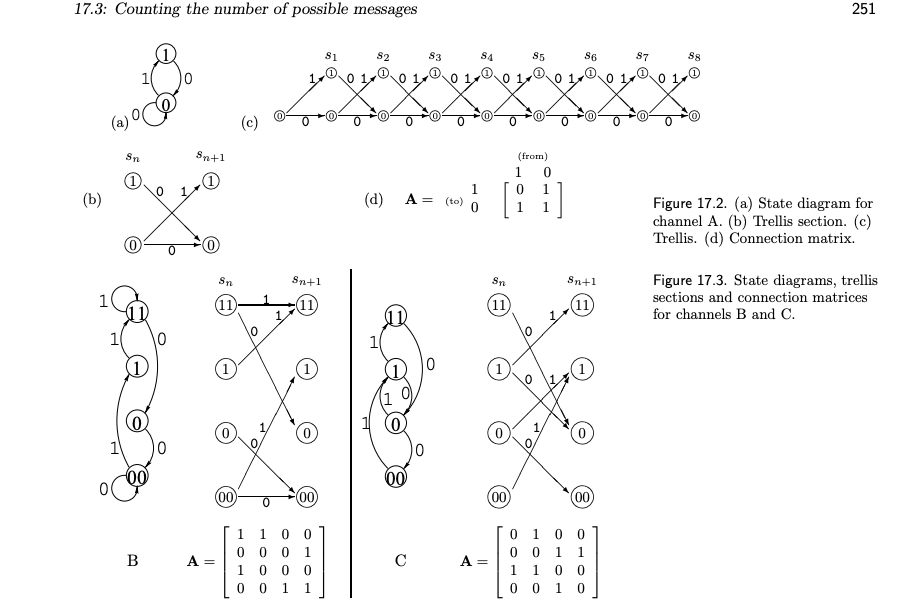
image-20230124010603224

(直觀且基本!) 計算 channel capacity 的構想: Path Counting

Noiseless channel capacity: $C = \lim_{n\to\infty} \max_{X^n} \frac{1}{n} H(X^n)$

另一個計算 channel capacity 的做法是計算有多少 “number of distinguishable messages”

\[C = \lim_{n\to\infty} \frac{1}{n} \log_2 M_n\]

Where $M_n$ : number of distinguishable messages. 更白話就是有多少不同的 (allowed) paths. 當然先決條件是每一條 path 都有相同的機率 (AEP).

用前文的例子說明：

  • Unconstraint noiselss channel $X^n = {x_1, x_2, .., x_n}$, 因為 $x_i \in {0, 1}$， 所以 “number of distinguishable messages” $M^n = 2^n \to C = \lim_{n\to\infty} \frac{1}{n} \log_2 2^n = 1$-bit，每一條 path (message) 的機率都是 $\frac{1}{2^{n}}$

  • 其實上述的 channel capacity 的定義 $C = \lim_{n\to\infty} \frac{1}{n} \log_2 M_n$ 可以推廣到 constraint noiseless channel! 甚至 noisy channel 或是 source of unequal probability

    • Unequal probability: 例如 $x_i = 1$ 的機率是 $p \ne 0.5$. 乍看之下也是 $M^n = 2^n$ paths. 但非所有 $2^n$ path 都有同樣的機率。事實上根據前文 (Info_Compress) AEP theorem：當 $n\to\infty$, 只有 $2^{nH(X)}$ paths 才有 equal probability, 並且總和無限接近 1! $M^n = 2^{nH(X)} \to C = \lim_{n\to\infty} \frac{1}{n} \log_2 2^{n H(X)} = H(X)$, 每一條 path (message) 的機率都是 $\frac{1}{2^{n H(X)}}$

    • Not surprise! 其實就是 source compression 的原理。可以推廣到 non-binary case.

    • Noisy memoryless channel: 前文 (Info_Comm1) 說明要產生 non-confusable subset, 需要把 $2^{nH(X)}$ 除以 $2^{n H(X Y)}$, 所以 distnguishable message 為 $M^n = 2^{nH(X)}/2^{nH(X Y)} = 2^{n(H(X)-H(X Y))} = 2^{n I(X;Y)}$

      $\to C = \lim_{n\to\infty} \frac{1}{n} \log_2 2^{n I(X;Y)} = I(X;Y)$

Path Counting of Noiseless Channel Capacity

我們用 “number of distinguishable messages” 計算 channel capacity

\[C = \lim_{n\to\infty} \frac{1}{n} \log_2 M_n\]

Channel A - 禁止 substring 11

我們先直接手算，如下圖。

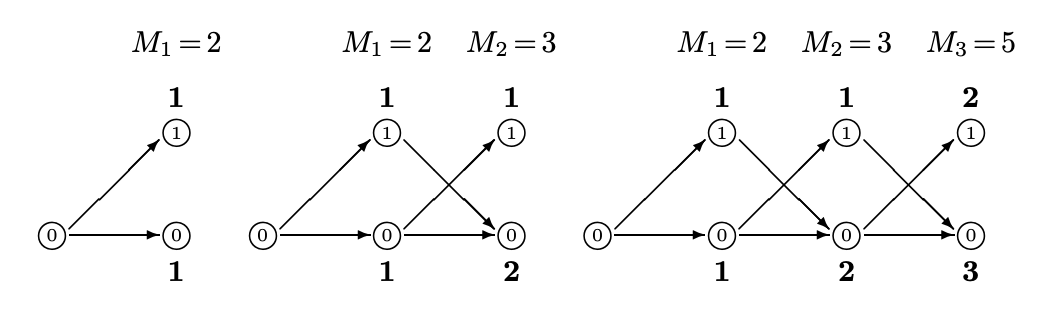
image-20230126000836144

再多算幾步如下：

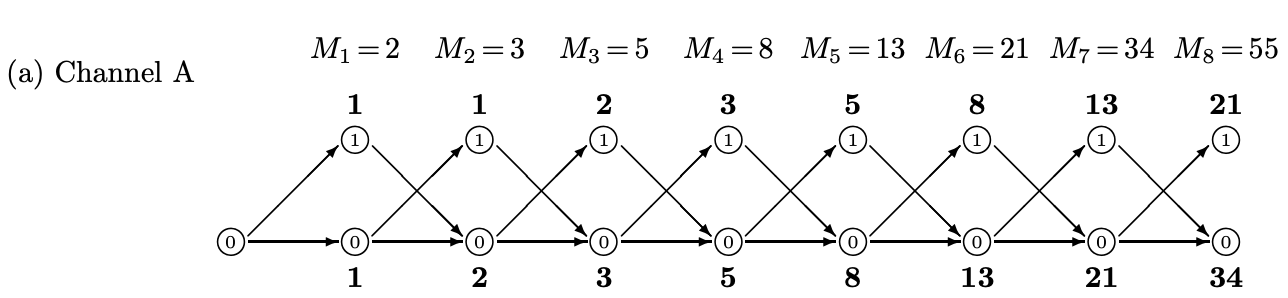
image-20230126001315411

  • $M_1 = a_1 + b_1 = 1 + 1 = 2$

  • $M_2 = a_2 + b_2 = b_1 + M_1 = 1 + 2 = 3$

  • $M_n = a_n + b_n = M_{n-2} + M_{n-1}$ 其中 $b_n = a_{n-1}+b_{n-1}=M_{n-1}$ and $a_n = b_{n-1} = M_{n-2}$

  • $M_n$ 是著名的 Fibonacci sequence, 如何計算 $\frac{1}{n}\log_2 M^n$?

  • 我們可以從 adjacent matrix $A$ of directed graph 得到 $a_n, b_n, M_n$ 的關係：

    • $S_n = A S_{n-1}$ where $S_n = [a_n, b_n]$ 是 n-time stamp 的所有 states (k=2).
    \[\left[\begin{array} {cc} a_n\\ b_n\end{array}\right]= \left[\begin{array} {cc}0 & 1\\ 1 & 1\end{array}\right] \left[\begin{array} {cc} a_{n-1}\\ b_{n-1}\end{array}\right]\]
    • $M_n = a_n + b_n$

  • $S_n = A^n S_0 = Q D^n Q^{-1} S_0$ 並且 $M_n = \sum_{k} S_n(k)$ where $S_n(k)$ 是 $S_n$ 的 $k$-th component

    • 此處用 eigenvalue decomposition 計算 $A^n = Q D^n Q^{-1}$ 此處 $D$ 是 eigenvalue 組成的 diagonal matrix.
    • 最大的 eigenvalue 似乎都是 real > 1 value. (how to prove?)
    • Perron-Frobenius theorem: dominant (largest) eigenvalue is bounded between the lowest sum of a row the biggest sum of a row
      • Transition probability matrix: dominant (largest) eigenvalue = 1 (因爲每一個 row sum 都是 1)
    • Theorem: 所有 eigenvalues 的和 = matrix trace!
    • 上例 largest eigenvalue 介於 [1, 2] , 第二個 eigenvalue [-1 0] 因爲 eigenvalue sum = 1!

  • $D^n = [1.62^n, 0; 0, (-0.62)^n]$ ， 當 $n\to\infty$, 只有 $1.62^n$ 不爲 0, 其他都是 0. 或者就算其他 eigenvalue 不小於 1, 但是最大 eigenvalue 的 n 次方後都可以忽略不計。 $D^n \simeq [\lambda_{max}^n, 0, ; 0, ; 0…]$ = $D^{n/2} D^{n/2} $

  • 所以 $Q D^n Q^{-1} = Q D^{n/2} D^{n/2} Q^{-1} \simeq [v_{max}, 0 0] \lambda^{n/2} \lambda^{n/2} [v_{max},0, ]’ = \lambda^n v_{max} \times v_{max}$ where $v_{max}$ is the largest eigenvalue’s eigen vector, x 是 cross-product.

  • 所以 $S_n = A^n S_0 = Q D^n Q^{-1} S_0 \simeq \lambda_{max}^n v_{max} \times v_{max} S_0 $

  • $M_n = [1,..,1] S_n \simeq \lambda_{max}^n [1, 1,.. 1] v_{max} \times v_{max} [0, 0 .., 1]’$

  • 頭是 [1, 1, 1, ] for Mn, 尾巴是 1-hot. 所以 $M_n \simeq \lambda_{max}^n v_{max} v_{max}(s_0)$
  • $C = \lim_{n\to\infty} \frac{1}{n} \log_2 M_n = \log_2 \lambda_{max}$, 因爲其他項在 $n\to\infty$ 都消失！

最後的結論是 $C = \log_2 \lambda_{max}$

Channel B - 禁止 substring 101 and 010

  • $a_n = a_{n-1} + b_{n-1}$; $b_n = d_{n-1}$; $c_n = a_{n-1}$; $d_n = c_{n-1} + d_{n-1}$
  • 其實這就是 adjacent matrix of directed graph! $S_n = A S_{n-1}$
  • \[\left[\begin{array} {cc} a_n\\ b_n \\ c_n \\ d_n \end{array}\right]= \left[\begin{array} {cc}1 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 \\1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1\end{array}\right] \left[\begin{array} {cc} a_{n-1}\\ b_{n-1} \\ c_{n-1} \\ d_{n-1} \end{array}\right]\]

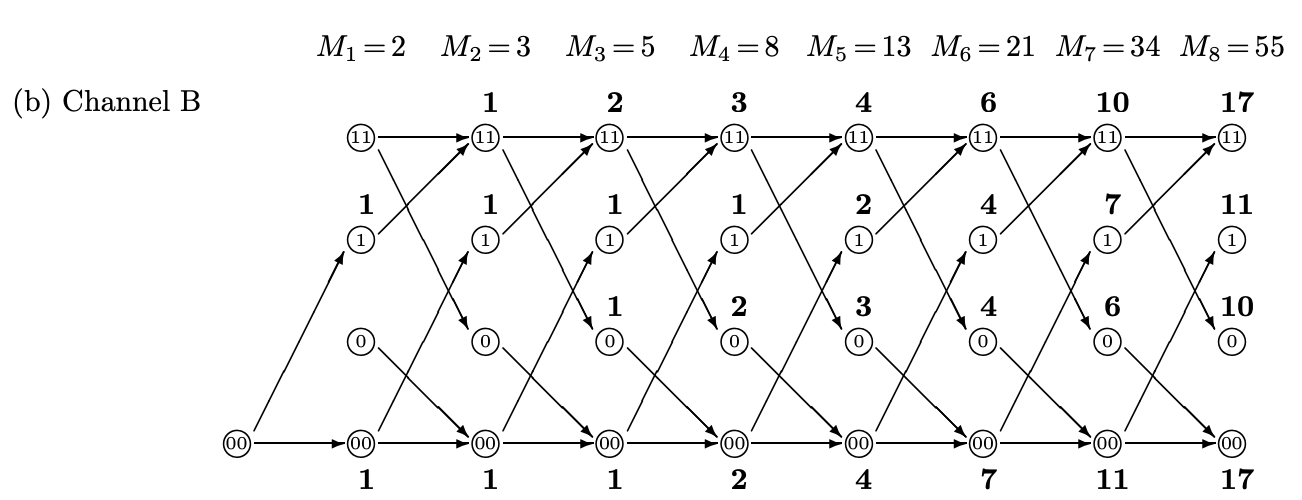
image-20230126003119027

Channel C - 禁止 substring 111 and 000

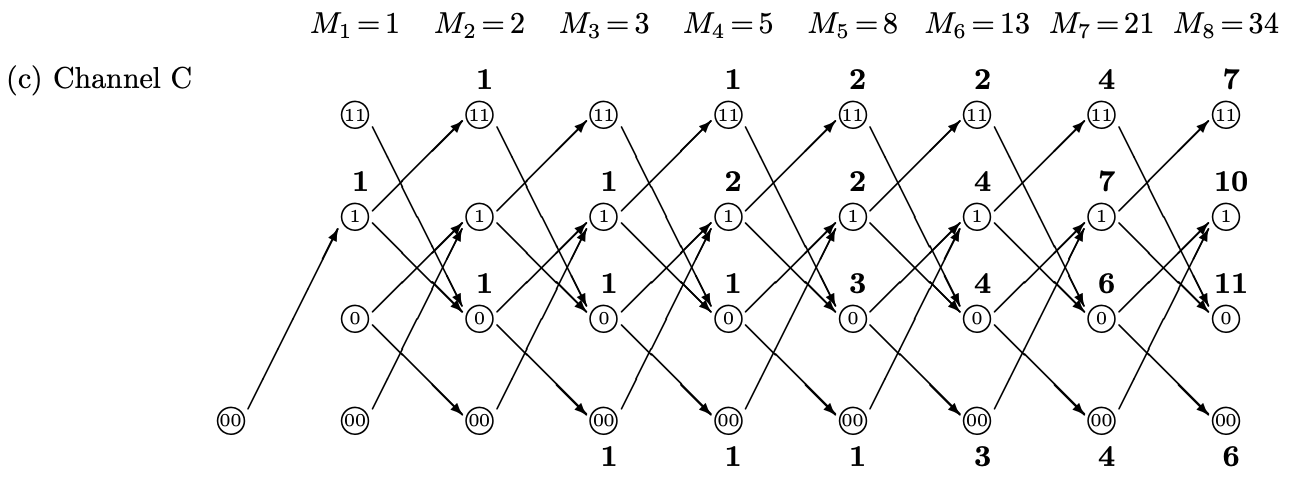
image-20230126003201575

有趣 channel A, B, C 都是一樣的 paths, 並且 $M_n$ 是著名的 Fibonacci series.

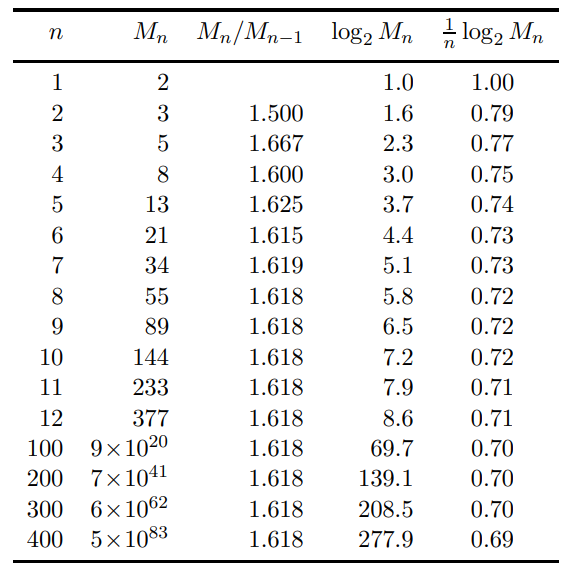
image-20230127184806353

Where $M_n$ : number of distinguishable messages. 更白話就是有多少不同的 (allowed) paths. 當然先決條件是每一條 path 都有相同的機率 (AEP).

can we do better than counting path? Not now!

Only depends on previous state ? Markov chain? Not really!

How about the transition probability? Different from the connection matrix!

(Wrong) 計算 noiseless channel capacity 的構想: Stationary Distribution

Noiseless channel capacity: $C = \lim_{n\to\infty} \frac{1}{n} \max_{X^n} \frac{1}{n} H(X^n)$

如果有 $X^n$ 的機率分佈，就可以計算 $H(X^n) = - \sum_i p(x^n_i) \log_2 p(x^n_i)$.

理論上 binary $X^n$ 有 $2^n$ 減掉 not allowed squences, 當 $n$ 很大，sequence 數目非常龐大。因為 $X^n$ sequence 有 inter-symbol dependence, 無法像 memoryless 化簡成一個 symbol 的 entropy/mutual information.

突破的關鍵是把 binary $X^n$ inter-symbol dependent sequence 轉換成 $k$ finite states, $S_k^n$, 簡稱 $S^n$, 的 Markov sequence/chain. 有什麼好處? 這部分是對的

  • Binary inter-symbol dependence 則可能 dependent on 前幾個 symbol (e.g. channel B, C). 而 Markov state sequence/chain, $S(t)$ Probability/entropy 只 dependent on 前一個 time stamp $S(t-1)$，是除了 independent symbol sequence 之外最容易處理/計算的 sequence.

  • Channel capacity: $C = \lim_{n\to\infty} \max_{X^n} H(X^n)/n = \lim_{n\to\infty} \max_{S^n} H(S^n)/n$

    • 此處 $S^n \equiv (s_1, s_2, …, s_n)$. 根據 Markov property: $p(S^n) = p(s_1, s_2, \cdots, s_n) = p(s_n s_{n-1},..,s_1) p(s_{n-1},..,s_1) $
      $= p(s_n s_{n-1}) p(s_{n-1},…,s_1) = \Pi_{i=1}^n p(s_i s_{i-1}) = B^n$

    • $C = \lim_{n\to\infty} \max_{X^n} H(X^n)/n = H(S^\infty) = - \sum_k p(S_k^\infty) \log_2 p(S_k^\infty)$ 注意這裏的 $k$ 是 (spatial) state domain, 不是 time domain sequence.

    • 如何計算 $p(S_k^{\infty})$? 這是 Markov chain 的標準習題。就是 transition (connection) matrix 的 eigenvalues!
  • (Wrong!) 根據 Markov chain ergodic (?) property: 時序 (time) sequence 的 probability distribution 可以轉換成 (spatial) stationary state probability distribution ==> 這部分概念是對的，
    • Yes! $\lim_{n\to\infty} p(x_i^n)/n = p(S^\infty)$
    • $p(S^{\infty}) = \lim_{n\to\infty} p(S^0) p(S^1 S^0)..p(S^n S^{n-1})$ 當 $n$ 夠大，initial distribution $S^0$ 不影響最終的 stationary state probability distribution
    • $C = \lim_{n\to\infty} \max_{X^n} H(X^n)/n = H(S^\infty) = - \sum_k p(S_k^\infty) \log_2 p(S_k^\infty)$ 注意這裏的 $k$ 是 (spatial) state domain, 不是 time domain sequence.
    • 如何計算 $p(S_k^{\infty})$? 這是 Markov chain 的標準習題。就是 transition (connection) matrix 的 eigenvalues!

  • 但是 $H(X^n) \ne H(S^{\infty})$!!!!!!

    • 舉例而言，如果 state 0 -> State 1 是 50%, 0 -> 0 是 50%, the Markov stationary probability 是 (2/3, 1/3) . H(1/3) =?
    • 但是 state 0 -> state 1 是 100%, 0 -> 0 是 0%, the markov stationary probability 是 (1/2, 1/2). H(1/2) > H(1/3)
    • 但是第二種情況， no information can be encoded!! stationary probability 是 deterministic!!!
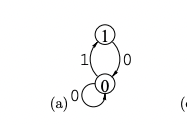
    • 所以不能用 stationary probability 取代中間所有的 path probability!! 沒有那麽簡單。 image-20230127233111231
  • (Wrong!!) State diagram 可以直接轉換成 transition (connection) matrix, done! 兩者完全不同！！

Channel A = [0 1; 1 1]. Symmetric -> real eigenvalues and orthogonal eigenvector

  • Eigenvalues = [1.62, -0.62] C = 0.694-bit; Eigenvector [0.53, 0.85]

我們把 adjacent matrix 變成 transition probability matrix

A = [0 1; p 1-p], what is the eigen vector for eigen-value = 1?

Channel B = [1 1 0 0; 0 0 0 1; 1 0 0 0; 0 0 1 1]. Symmetric -> real eigenvalues and orthogonal eigenvector

  • Eigenvalues = [1.618, -0.618, 0.5+/-0.866i] C = 0.694-bit; Eigenvector [0.60, 0.37, 0.37, 0.60]

Channel C = [1 1 0 0; 0 0 0 1; 1 0 0 0; 0 0 1 1]. Symmetric -> real eigenvalues and orthogonal eigenvector

  • Eigenvalues = [1.618, -0.618, 0.5+/-0.866i] C = 0.694-bit; Eigenvector [0.60, 0.37, 0.37, 0.60]

好像混淆 Markov chain long term probability -> eigenvector but with transition matrix sum to 1 (not the current matrix!!!)

How about plus noise? Similar, but using Viterbi or dynamic programming

Citation