Main Reference
二次型與正定矩陣: 線代啟示錄 (wordpress.com)http://www-personal.umich.edu/~mmustata/Slides_Lecture13_565.pdf)
二次式
二次式大概是數學和物理最重要的形式。不論是求解、極值(最大或最小)、非綫性、簡諧運動等等都和二次式相關。矩陣也不例外。
有了二次式就可以定義正定矩陣,Rayleigh Quotient, Courant-Fischer Theorem, etc. 二次式和 eigenvalues 直接相關。
令 $A=\left[a_{i j}\right]$ 為一個 $n \times n$ 實矩陣, $\mathbf{x}=\left[\begin{array}{c}x_1 \ \vdots \ x_n\end{array}\right]$ 為 $n$ 維實向量, 具有以下形式的實函數稱為 二次型 (quadratic form) : \(f(\mathbf{x})=\mathbf{x}^T A \mathbf{x} 。\)
- 注意:二次型 $\mathbf{x}^T A \mathbf{x}$ 是一個純量。
- 任意二次型 $\mathbf{x}^T A \mathbf{x}$ 都可以轉換為等價的 $\mathbf{x}^T B \mathbf{x}$, 其中 $B$ 是一個實對稱矩陣:$B=\frac{1}{2}\left(A+A^T\right)$
- 利用一點運算技巧改寫矩陣乘法公式可得
\(\begin{aligned} \mathbf{x}^T A \mathbf{x} & =\sum_{i=1}^n \sum_{j=1}^n a_{i j} x_i x_j \\ & =\sum_{i=1}^n \sum_{j=1}^n \frac{1}{2}\left(a_{i j}+a_{j i}\right) x_i x_j \\ & =\mathbf{x}^T\left[\frac{1}{2}\left(A+A^T\right)\right] \mathbf{x} \end{aligned}\)
- 矩陣 $A$ 與 $B=\frac{1}{2}\left(A+A^T\right)$ 有相等的二次型, 不難驗證 $\frac{1}{2}\left(A+A^T\right)$ 是對稱的。例如,
正定矩陣
定義
令 $A$為一個 $n\times n$ 階實對稱矩陣。若每一 $n$ 維非零實向量 $\mathbf{x}$ 皆使得 $\mathbf{x}^TA\mathbf{x}>0$,我們稱 $A$ 為正定 (positive definite);若將上述條件放鬆為 $\mathbf{x}^TA\mathbf{x}\ge 0$,則 $A$ 稱為半正定 (positive semidefinite)。如果 $\mathbf{x}^TA\mathbf{x}$可能是正值也可能是負值,則稱 $A$ 是未定的 (indefinite)。
傳統上,我們習慣將對稱性納入正定矩陣的定義,一方面因為實對稱正定矩陣擁有美好的性質,另一個原因是實對稱正定矩陣的分析就足以應付其他一般的正定矩陣。
- 任意二次型 $\mathbf{x}^T A \mathbf{x}$ 都可以轉換為等價的 $\mathbf{x}^T B \mathbf{x}$, 其中 $B$ 是一個實對稱矩陣:$B=\frac{1}{2}\left(A+A^T\right)$
- 如果 $A$ 是正定或半正定矩陣,則實對稱矩陣 $B$ 也是正定或半正定矩陣。
- 如何判斷 $A$ 是正定或半正定矩陣?顯然不可能試所有的 $\mathbf{x}^TA\mathbf{x} > 0$.
- 最直接的方法就是看 eigenvalues. 如果所有 eigenvalues 都大於 0, 為正定矩陣。如果所有 eigenvalues 都大於等於 0, 為半正定矩陣。
- 注意:如果 $A$ 不是對稱矩陣,eigenvalues 有可能是複數。此時判斷 $B = \frac{1}{2}(A+A^T)$ 的 eigenvalues. 因爲 $B$ 是對稱矩陣,所有 eigenvalues 一定都是實數。
- 證明:假設 $A$ 是對稱矩陣,$A = Q D Q^T \to \mathbf{x}^T A \mathbf{x} = \mathbf{x}^T Q D Q^T \mathbf{x} = \mathbf{z}^T D \mathbf{z} = \lambda_1 z_1^2 + … + \lambda_n y_n^2$
- 如果 $\lambda_k > 0, \, \mathbf{x}^T A \mathbf{x} > 0 \to A $ 是正定矩陣
- 如果 $\lambda_k \ge 0, \, \mathbf{x}^T A \mathbf{x} \ge 0 \to A $ 是半正定矩陣
幾何意義
考慮 $n=1$ 的情況,矩陣 $A$ 和向量 $\mathbf{x}$ 分別退化為純量 $a$ 和 $x$,如果對任意非零 $x$ 都有 $xax=ax^2>0$。
我們說 $a$ 是正定的,或簡潔地說 $a$ 是正的 ($a>0$),則 $ax$ 與 $x$ 有相同的正負號。當 $n>1$ 時,令 $\theta$ 為 $A\mathbf{x}$ 與 $\mathbf{x}$ 的夾角,此夾角的餘弦為
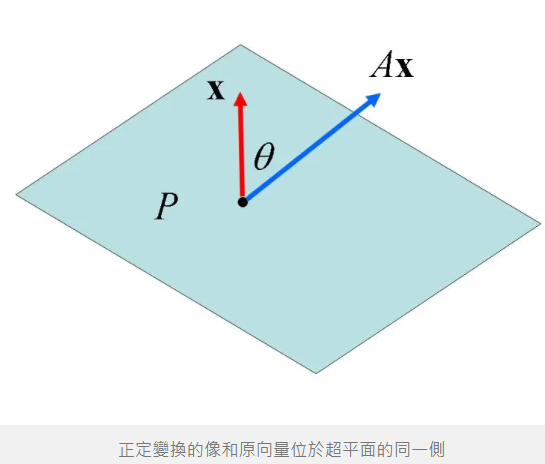
\[\cos\theta=\displaystyle\frac{\mathbf{x}^T(A\mathbf{x})}{\Vert\mathbf{x}\Vert~\Vert A\mathbf{x}\Vert}\]上式中,$A\mathbf{x}$ 與 $\mathbf{x}$ 的內積為正值表示經線性變換後的向量 $A\mathbf{x}$ 與原向量 $\mathbf{x}$ 的夾角小於 $90^{\circ}$。見下圖,$\mathbf{x}$ 為超平面 $P$ 的法向量,正定矩陣 $A$ 保證變換後的向量 $A\mathbf{x}$ 與原向量 $\mathbf{x}$ 都位於超平面 $P$ 的同一側。
實數對稱矩陣 or Complex Hermitian Matrix 定理
特徵值的重要定理:Courant-Fischer min-max theorem
本定理是針對複數 Hermitian matrix 或是實數矩陣, $A = A^*$ (complex matrix) or $A = A^T$ (real matrix)
實數對稱矩陣 (或複數 Hermitian matrix) 有獨特的地位:
- Eigenvalues 均爲實數,Eigenvectors 互相正交。證明很容易 $A x = A^* x = \lambda x \to x^* A = \lambda^* x^* \to x^* A x = \lambda^* x^* x \to x^* \lambda x = \lambda^* x x^* \to \lambda = \lambda^*$
-
EVD 和 SVD 基本一致,不過 eigenvalues and eigenvectors 可能差正負號。代表 invariant eigenvectors 也是正交 basis.
- $x^* A x$ : 對於任意 column vector 向量 $x \in \C$, $x^* A x$ 為實數。(這對複數 vector 很重要,對於實數 vector trivial).
- 證明:$x^* A x = x^* Q D Q^* x = z^* D z = \sum_i \lambda_i |z_i|^2 \in \R$ 因爲 $\lambda_i \in \R$
- 以 2D SVD 爲例,正交 basis 就是單位圓 vector $|x|=1$ 經過 $Ax$ mapping 後產生最大和最小的 vector. 因爲是對稱矩陣,SVD 和 EVD 一致,所以 $\lambda_{max}$ 對應最大的 $|Ax|$, 所以 $\lambda_{min}$ 對應最小的 $|Ax|$
- $\lambda_{max} = \max \frac{x^* A x}{x^* x}$
- $\lambda_{min} = \min \frac{x^* A x}{x^* x}$
- 那麽 3D, 4D 或更高維的 eigenvalues 又是如何呢?這就是 Courant-Fischer min-max theorem
Rayleigh Quotient
-
定義 Rayleigh Quotient: $R = \frac{x^* A x}{x^* x}$ where $x \ne 0$
-
Given $A$ 是 $n \times n$ 的 Hermitian matrix (or real symmetric matrix), eigenvalues 皆爲實數。假設 $\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_n$, 對應的正交 eigenvectors 為 $u_1, u_2, …, u_n$則有
- $\max R = \max \frac{x^* A x}{x^* x} = \lambda_1$ when $x = k u_1$
- $\min R = \min \frac{x^* A x}{x^* x} = \lambda_n$ when $x = k u_n$
-
證明:$R = \frac{x^* A x}{x^* x} = \frac{x^* Q D Q^* x}{x^* x} = \frac{z^* D z}{z^* z} = \frac{\sum_i \lambda_i z_i ^2 }{\sum_i z_i }$ 因此 $ \lambda_n \le R \le \lambda_1$ - $z = Q^* x$ 並且 $x^* x = z^* z$
-
直觀看出如果是和 $u_1$ 正交的空間 $(0, u_2, …, u_n )$ 的 Rayleigh Quotient 最大值是 $\lambda_2$, i.e.
-
$\max_{x \perp u_1} \frac{x^* A x}{x^* x} = \max_{x^* u_1 = 0} \frac{x^* A x}{x^* x} =\max_{x \in (u_2, .. u_n)} \frac{x^* A x}{x^* x} = \lambda_2$
- 同樣的邏輯,$\max_{x \in (u_k, .. u_n)} \frac{x^* A x}{x^* x} = \lambda_k$
- 比較有趣是,最後 eigenvalue $\max_{x \in (u_n)} \frac{x^* A x}{x^* x} = \lambda_n = \min_{x} \frac{x^* A x}{x^* x}$
-
上式必須知道 $u_1$ 是否有方法繞過 $u_1$? Yes, 利用 min
-
考慮任意向量 $w \in \C$ 且 $x \perp w \to z \perp Q^* w$, 令 $V = {z z\perp Q^* w}$, 且 $V’ = {z z\perp Q^* w, z_3 = z_4 … = z_n =0}$, 則有 $V’ \subset V$ - $\max_{x \perp w} \frac{x^* A x}{x^* x} = \max_{z \perp Q^* w} \frac{z^* D z}{z^* z} = \max_{z \in V} \frac{z^* D z}{z^* z}$ $ \ge \max_{z \in V’} \frac{z^* D z}{z^* z} = \max_{z \in V’} \frac{\lambda_1 |z_1|^2 + \lambda_2 |z_2|^2}{|z_1|^2 + |z_2|^2} \ge \lambda_2$
- 等號成立當 $w = u_1$
-
-
因此 $\min_w \max_{x \perp w} \frac{x^* A x}{x^* x} = \lambda_2$
- 這公式有點難看懂。就是任意的 (n-1) 維子空間,所有最大值中的最小值是 $\lambda_2$. 仔細想一下,如果 $w \nparallel u_1$, (n-1) 維子空間一定包含 $u_1$, R 的最大值是 $\lambda_1$; 只有當 $w \parallel u_1$, (n-1) 維子空間不包含 $u_1$, R 的最大值是 $\lambda_2 \le \lambda_1$, 才是正解。因此可以用 $\min_w$ 取代 $w = u_1$.
-
反過來 $\max_w \min_{x \perp w} \frac{x^* A x}{x^* x} = \lambda_{n-1}$
- 就是任意的 (n-1) 維子空間,所有最小值中的最大值是 $\lambda_{n-1}$. 仔細想一下,如果 $w \nparallel u_n$, (n-1) 維子空間一定包含 $u_n$, R 的最小值是 $\lambda_n$; 只有當 $w \parallel u_n$, (n-1) 維子空間不包含 $u_n$, R 的最小值是 $\lambda_{n-1} \ge \lambda_n$. 因此可以用 $\max_w$ 取代 $w = u_n$.
-
同樣 $\min_{w_1, w_2} \max_{x \perp w_1, w_2} \frac{x^* A x}{x^* x} = \lambda_3$
- 就是任意的 (n-2) 維子空間,所有最大值中的最小值是 $\lambda_3$. 如果 (n-2) 維子空間包含 $u_1$ 或 $u_2$, R 的最大值是 $\lambda_1$ 或 $\lambda_2$; 只有當 (n-2) 維子空間不包含 $u_1, u_2$, R 的最大值是 $\lambda_3 \le \lambda_1, \lambda_2$, 才是正解。因此可以用 $\min_{w_1, w_2}$ 取代 $w_1 = u_1, w_2 = u_2$.
-
反過來 $\max_{w_1, w_2} \min_{x \perp w_1,w_2} \frac{x^* A x}{x^* x} = \lambda_{n-2}$
-
Courant-Fischer Min-Max Theorem Summary
對於 $n \times n$ 的 Hermitian matrix (或是實數的對稱矩陣):
$\lambda_k$ 是 $k$-th 大的 eigenvalue, i.e. $\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_n$
- $\lambda_k = \min_{dim(V)=n-k+1} \max_{x \in V} R = \min_{dim(V)=n-k+1} \max_{x \in V} \frac{x^* A x}{x^* x}$
- $\lambda_k = \max_{dim(V)=k} \min_{x \in V} R = \max_{dim(V)=k} \min_{x \in V} \frac{x^* A x}{x^* x}$
應用 1: Constrained Optimization
最大化 $\mathbf{x}^T A \mathbf{x}, \mathbf{x}$ 滿足 $|\mathbf{x}|^2=\mathbf{x}^T \mathbf{x}=1$ 。
求解這個約束最佳化 (constrained optimization) 問題的傳統方法是引入 Lagrangian multiplier: \(L(\mathbf{x}, \lambda) \equiv \mathbf{x}^T A \mathbf{x}-\lambda\left(\mathbf{x}^T \mathbf{x}-1\right)\) 產生極值的必要條件是 $L$ 對 $\mathbf{x}$ 的各元的一次偏導數都等於零, 亦即 $\mathrm{x}$ 是 $L$ 的一個駐點。因為 $A^T=A$, 請讀者自行計算驗證 \(\mathbf{0}=\nabla_{\mathbf{x}} L=2(A \mathbf{x}-\lambda \mathbf{x}) 。\) 單位向量 (unit vector) $\mathbf{x}$ 要使 $\mathbf{x}^T A \mathbf{x}$ 最大化的必要條件即為特徵方程式 $A \mathbf{x}=\lambda \mathbf{x}$, 將此式代 人二次型可得 \(\mathbf{x}^T A \mathbf{x}=\mathbf{x}^T(\lambda \mathbf{x})=\lambda\|\mathbf{x}\|^2=\lambda^{\circ}\) 實對稱矩陣的特徵值必為實數, 因此使二次型最大化的向量 $\mathbf{x}$ 正是對應最大特徵值的特徵 向量。
應用 2: 估計 Hermitian 矩陣最大特徵值的下界和最小特徵值的上界
Rayleigh 定理的幾何意義是如果限制 $\mathbf{x}$ 為單位向量, $\lambda_1$ 和 $\lambda_n$ 給出二次型 $\mathbf{x}^* A \mathbf{x}$ 的最大值與 最小值。考慮 $\mathbf{e}i=(0, \ldots, 0,1,0, \ldots, 0)^T$, 其第 $i$ 個元素為 1 , 則 $\mathbf{e}_i^* A \mathbf{e}_i=a{i i}{ }^{\circ}$ Rayleigh 定 理有這個必然結果: Hermitian 矩陣 $A=\left[a_{i j}\right]$ 的任意主對角元也落在 $\lambda_1$ 和 $\lambda_n$ 之間,即 $\lambda_n \leq a_{i i} \leq \lambda_1$ 。利用此性質可約略估計 Hermitian 矩陣最大特徵值的下界和最小特徵值的上界。另外 $tr(A) = \sum_k^n \lambda_k$.
例如 \(A=\left[\begin{array}{lll} 1 & 2 & 3 \\ 2 & 5 & 4 \\ 3 & 4 & 9 \end{array}\right]\) 不需經過計算也可推知 $A$ 的最大特徵值不小於 9 ,最小特徵值不大於 1 。eigenvalues: (12.6, 2.5, -0.1)
應用 3: Wely Theorem
對於兩個 $n \times n$ 的 Hermitian matrix (or real symmetric matrix) $A$ and $B$:
\(\lambda_k(A) + \lambda_n(B) \le \lambda_k (A+B) \le \lambda_k(A) + \lambda_1(B)\) 有用的結論
-
兩個 Hermitian matrixes 的 eigenvalues 範圍
-
一個 Hermitian matrix 加上一個 semi-definite matrix (所有 eigenvalues 大於等於 0), eigenvalues 必增大
應用 4: Variation Method (Why Variation?)
Let $A, B \in \mathbb{R}^{n \times n}, A^T=A, B^T=B>0$ and $\lambda_1 \leq \lambda_2 \leq \ldots \lambda_n$ be the eigenvalues of $A u=\lambda B u$ with corresponding eigenvectors $u_1, u_2, \ldots, u_n$,
then
\[\min _{x} \frac{x^T A x}{x^T B x}=\lambda_1, \quad \arg \min _{x} \frac{x^T A x}{x^T B x}=u_1 .\]and
\[\min _{x^T B u_1=0} \frac{x^T A x}{x^T B x}=\lambda_2, \quad \arg \min _{x^T B u_1=0} \frac{x^T A x}{x^T B x}=u_2 .\]- $A u=\lambda B u \to (A-\lambda B)u = 0 \to B^{-1}(A-\lambda B)u = 0 \to B^{-1}A u - \lambda u = 0$
- eigenvalues and eigenvectors 等價 $B^{-1} A$ 的 eigenvalues and eigenvectors.
- $B = I$ 就是 Courant-Fischer 定理。這是一個推廣。
- For the matrix pair $(L, D)$, it is known that $\left(\lambda_1, y_1\right)=(0,1)$.
- By the variational principle, the relaxed minimal Ncut (2) is equivalent to finding the second smallest eigenpair $\left(\lambda_2, y_2\right)$ of
Remarks:
-
$L$ is extremely sparse and $D$ is diagonal;
-
Precision requirement for eigenvectors is low, say $\mathcal{O}\left(10^{-3}\right)$.