Main Reference
圖和矩陣 Graph and (Adjacency) Matrix
所有 graph 的定義都包含 $G(V, E)$:V 是頂點或節點 (Vertex),E 是邊 (Edge)。Edge 可以是無方向的稱爲無向圖 (undirected graph). 或是有方向的稱爲有向圖 (directed graph). 甚至混合的稱爲 mixed graph.
| 下圖我們用 | V | 表示節點數目, | E | 表示邊的數目。 |

不過更重要的是所有的 graphs 都可以用 matrix 表示。這很重要,因爲可以用 linear algebra on graph.
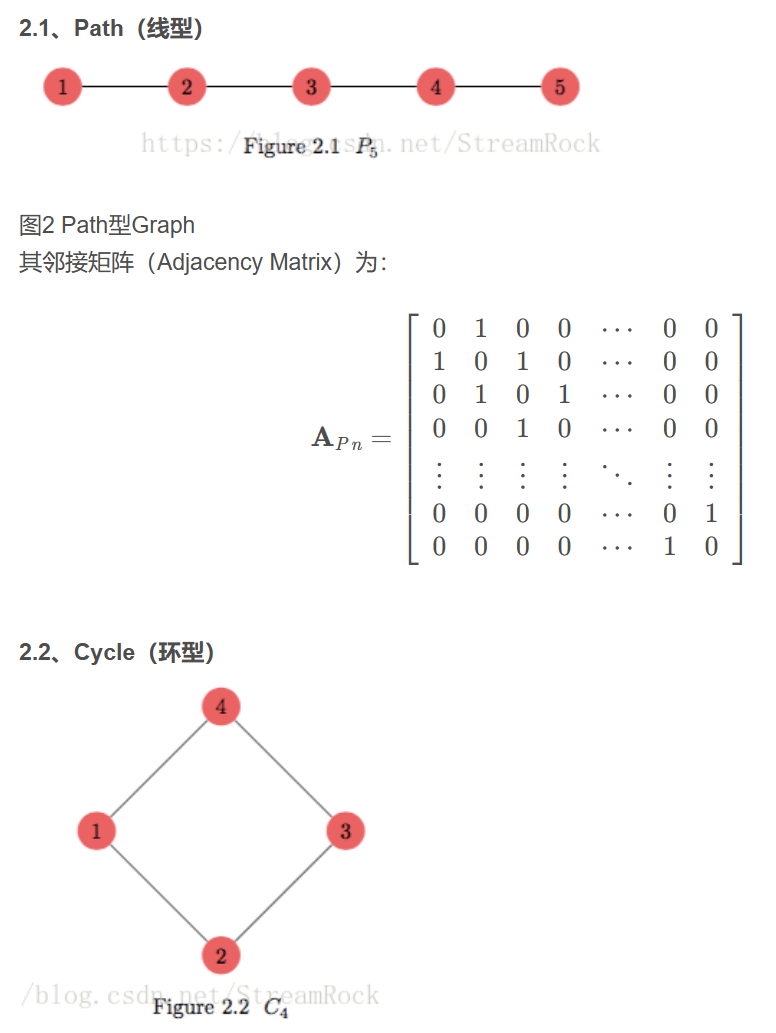
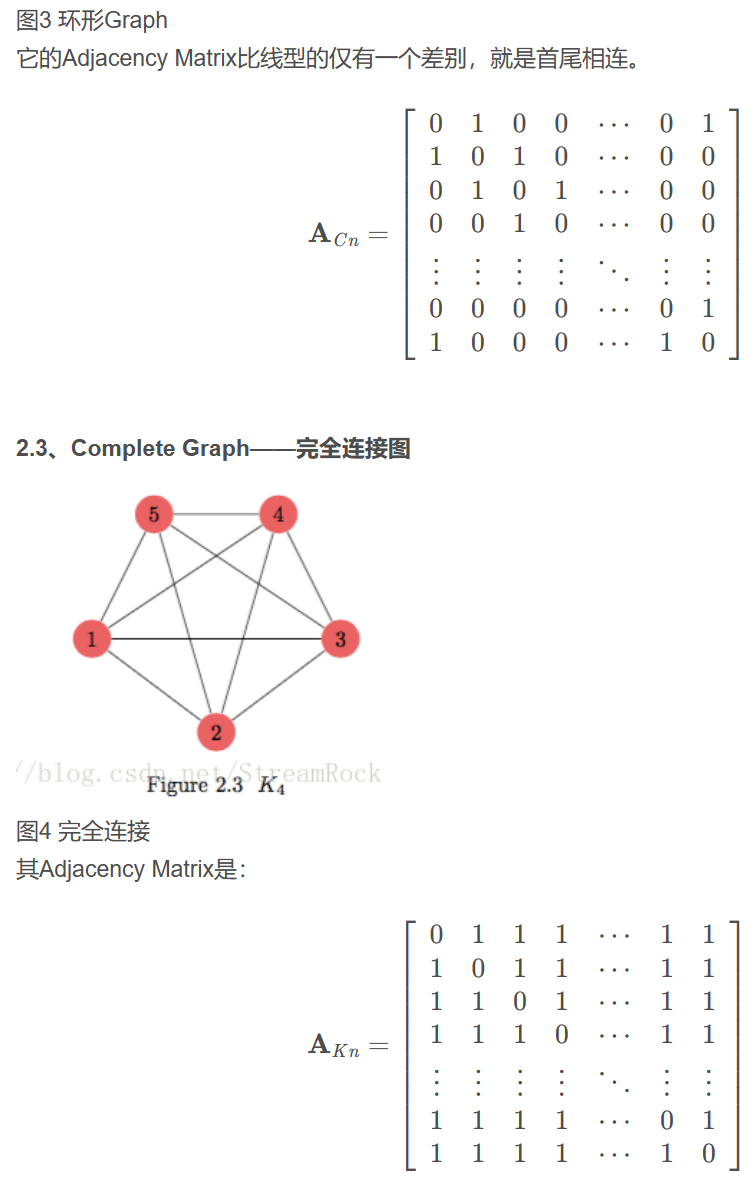
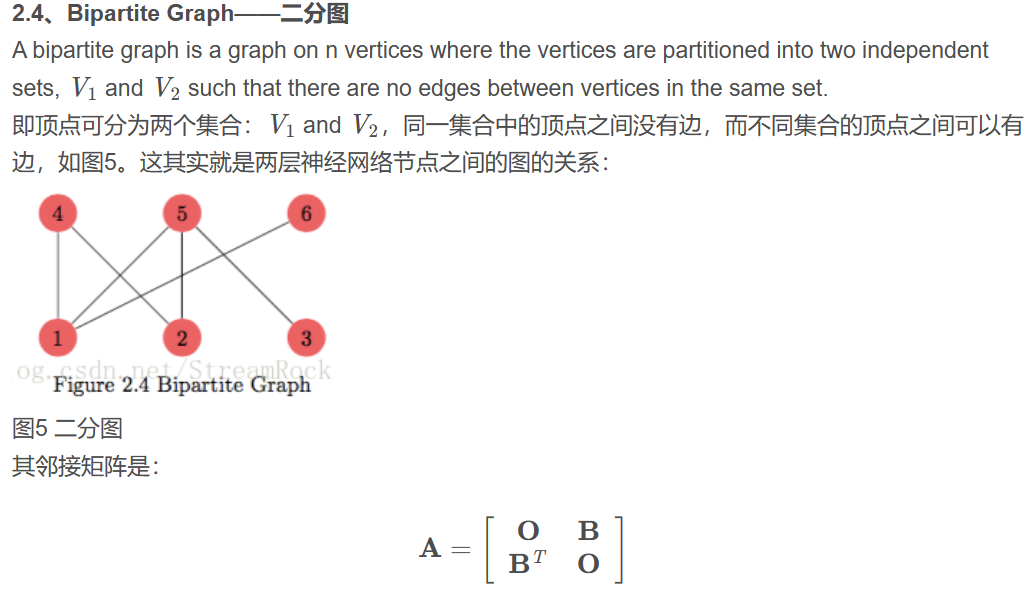
- 最常用的是鄰接矩陣 (adjacency matrix), $A$:任何相連的 vertex 對應的 edge 為 1, 其餘為 0. 所以也稱爲 connection matrix. Edge 可以是無方向,也可以是有方向的。如果 edge 無方向稱爲無向圖 (undirected graph),如果 edge 有方向就稱爲有向圖 (directed graph)。
- 無向圖 (undirected graph) 的鄰接矩陣是對稱矩陣 symmetric matrix,一般 trace = 0. (見上圖)
- 有向圖 (directed graph) 的鄰接矩陣一般是非對稱矩陣 symmetric matrix 且 trace $\ne 0$. (見上圖)
- 另一個是 degree matrix, $D$:每個節點的 edge number. 是 diagonal matrix, 一定是對稱 matrix. (見下圖)
- 每個頂點的度 (degree of a vertex) : $d(v_i) = \sum_{j=1}^n a_{ij}$
- $D = D(G) = diag(d(v_1), d(v_2), …, d(v_n))$
-
$D$ 的 trace = $\sum_{i=1}^n d(v_i) = \sum_{i=1}^n \sum_{j=1}^n a_{ij} = 2 E $, 因爲所有 edge 都被計算兩次。
- 還有非常重要的 Laplacian matrix:$L = D - A$
- $L$ 每個列向量的和為 0, 所以 $L$ (1) not full rank; (2) 至少一個 eigenvalue = 0; (3) determinant $\det(L) = 0$
-
$D-A$ (而非 $A-D$) **的 trace = 2 E ** > 0! 才能得到大於等於 0 的 eigenvalues

Simple Graph Adjacency Matrix
Laplacian Matrix 物理意義
$x^T L x = \frac{1}{2} \sum_{i,j=1}^n a_{ij} (x_i-x_j)^2$ for $\forall x \in \R^n$
-
證明:$\frac{1}{2} \sum_{i,j=1}^n a_{ij} (x_i-x_j)^2 = \sum_{i=1}^n a_{ii} x_i^2 - \sum_{i\ne j} a_{ij} x_i x_j = x^T L x = x^T (D - A) x$
-
2D 例子 :
-
2D Symmetric Laplacian Matrix:$L = \left[\begin{array}{cc} 1 & -1\ -1 & 1\end{array}\right]$ $d_1 = a_{12} = d_2 = a_{21} =1 $ \(\begin{aligned}x^T L x &= d_1 x_1^2 + d_2 x_2^2 - (a_{12}+a_{21}) x_1 x_2 \\&= [a_{12} (x_1 - x_2)^2] = \frac{1}{2}[a_{12} (x_1 - x_2)^2 + a_{21} (x_2 - x_1)^2 ] \\&= \frac{1}{2} \sum_{i,j=1}^2 a_{ij} (x_i - x_j)^2 \end{aligned}\)
-
3D 例子 :
- 3D Symmetric Laplacian Matrix:$d_1 = a_{12} + a_{13} ; d_2 = a_{21} + a_{23} ; d_3 = a_{31} + a_{32}$ and $a_{ij} = a_{ji}$ \(\begin{aligned}x^T L x &= d_1 x_1^2 + d_2 x_2^2 + d_3 x_3^2 - (a_{12}+a_{21}) x_1 x_2 - (a_{13}+a_{31}) x_1 x_3 - (a_{23}+a_{32}) x_2 x_3 \\ &= a_{12} (x_1 - x_2)^2 + a_{13} (x_1 - x_3)^2 + a_{23} (x_2 - x_3)^2 \\&= \frac{1}{2} \sum_{i,j=1}^3 a_{ij} (x_i - x_j)^2 \end{aligned}\)
Graph Spectrum 觀念 (Eigenvalues)
圖的特徵值 Graph‘s Eigenvalue
先提示一些 eigenvalue 相關的定理
用 2x2 matrix 為例子
Eigenvalue 和 eigenvector 加入作爲代數的判斷,定義如下: \(\left[\begin{array} {cc}a_{11} & a_{12}\\a_{21} & a_{22}\end{array}\right] \left[\begin{array} {cc}v_{1} \\v_{2}\end{array}\right]= \lambda \left[\begin{array} {cc}v_{1} \\v_{2}\end{array}\right]\)
\[(a_{11}-\lambda)(a_{22}-\lambda) - a_{21}a_{12} = 0 \\ \lambda^2 - (a_{11}+a_{22})\lambda + (a_{11} a_{22}-a_{12}a_{21}) = 0 \\ \lambda = \frac{a_{11}+a_{22}\pm \sqrt{(a_{11}+a_{22})^2-4(a_{11} a_{22}-a_{12}a_{21})}}{2} \\ \lambda = \frac{a_{11}+a_{22}\pm \sqrt{(a_{11}-a_{22})^2+4 a_{12}a_{21}}}{2}\]相似矩陣
-
$P^{-1} A P = B$ 若 $P$ 是 invertable, $A, B$ 稱爲相似矩陣 (similar matrix).
- Similar matrix $A, B$ 有相同 (1) rank; (2) eigenvalues (but not eigenvector!); (3) determinant.
- 可以證明:$A$ (nxn) 和 $A^T$ (nxn) 是相似矩陣:有相同的 rank, eigenvalues (but not eigenvectors!), determinant.
-
Eigenvalue decomposition: $A = Q D Q^{-1}$, 所以 $A, D$ 是相似矩陣:相同 rank, eigenvalues, determinant.
- 如果 $A$ 是對稱 matrix, 所有 eigenvalues 都是實數。所有 eigenvectors 都正交 $Q^{-1} = Q^T$
- Trace theorem: 所有 eigenvalues 的和 = matrix trace, i.e. tr(A) = tr(D)
實數對稱矩陣 (Special Case of Complex Hermitian Matrix)
- Eigenvalue decomposition (EVD, invariant basis) 和 Singular value decomposition (SVD, orthogonal basis) 的 eigen-values 和 singular values 以及 eigen-vectors 和 singular vectors 基本一樣,最多差一個正負號。
- Eigenvalues 是實數, i.e. $\lambda_k^* = \lambda_k$ (非對稱矩陣可能有複數 eigenvalues)
- Eigenvectors 是正交 vectors, i.e. $Q Q^* = I$, where $Q$ 的 column vectors 是 (right) eigenvectors, $u_k$.
- $Q = [u_1, u_2, …, u_n]$ and $Q Q^* = I \to u_i u_j^* = \delta_{ij}$
- $Q Q^* = I \to Q^{-1} = Q^* to A = Q D Q^{-1} = Q D Q^*$
- Courant-Fischer min-max 定理,對於 $n \times n$ 的 Hermitian matrix (或是實數的對稱矩陣):
- $x^* A x$ 一定是實數
- $\lambda_k$ 是 $k$-th 大的 eigenvalue, i.e. $\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_n$
- $\lambda_k = \min_{dim(V)=n-k+1} \max_{x \in V} R = \min_{dim(V)=n-k+1} \max_{x \in V} \frac{x^* A x}{x^* x}$
- $\lambda_k = \max_{dim(V)=k} \min_{x \in V} R = \max_{dim(V)=k} \min_{x \in V} \frac{x^* A x}{x^* x}$
- Wyle 定理
- 兩個 Hermitian matrixes 的 eigenvalues 範圍
- 一個 Hermitian matrix $A$ 加上一個 semi-definite matrix $B$ (all $\lambda_k \ge 0$), $A+B$ eigenvalues 必增大
Diagonal Dominant Matrix
最重要的結論:Laplacian matrix 是 weakly diagonal dominance : positive semi-definite.
- Laplacian matrix 的所有 eigenvalues 都大於或等於 0.
- Laplacian matrix 是 singular 因爲最小的 eigenvalue 為 0.
如果矩陣 $A$ 每個 row 的對角元素大於等於其他所有非對角元素和,稱爲 diagonally dominant matrix.
-
Weakly (有等號) diagonal dominance: $ a_{ii} \ge \sum_{i\ne j} a_{ij} $ for all $i$ -
Strictly (沒等號) diagonal dominance: $ a_{ii} > \sum_{i\ne j} a_{ij} $ for all $i$ -
例一:$\left[\begin{array} {cc}3 & -2 & 1 \ 1 & -3 & 2 \-1 & 2 & 4\end{array}\right],$ Strick diagonal dominance.
-
例二:Laplacian matrix $\left[\begin{array}{cc} d_1 & -a_{12} & -a_{13}\ -a_{21} & d_2 & -a_{23} \ -a_{31} & -a_{32} & d_3\end{array}\right]$, Weak diagonal dominance.
-
例三:band matrix $\left[\begin{array}{cc} d_1 & a_{12} & 0\ a_{21} & d_2 & a_{23} \ 0 & a_{32} & d_3\end{array}\right]$, 如果 $ d_i > \sum_j a_{ij}$ -
Gershgorin’s circle theorem:
- Strictly diagonal dominance (Laplacian matrix 不屬於此例):non-singular.
- Hermitian (or real symmetric) and strictly diagonal dominance (Laplacian matrix 不屬於此例) : positive definite.
- Hermitian (or real symmetric) and weakly diagonal dominance (Laplacian matrix 屬於此例) : positive semi-definite.
全正矩陣
- Perron-Frobenius theorem: for all positive element matrix, the dominant (largest) eigenvalue is bounded between the lowest sum of a row the biggest sum of a row. 並且 dominant eigenvalue 對應全正值 (或全負值 x -1) 的 eigenvector.
無向圖的特徵值 Undirected Graph’s Eigenvalue
無向圖 (undirected graph) 的鄰接矩陣 $A$ 是對稱矩陣 symmetric matrix 且 Trace = 0,所以:
-
所有 eigenvalues 都是實數,所有的 eigenvectors 都是正交 vectors。
-
最大的 eigenvalue 介於最大和最小的 degree 之間 (Perron-Frobenius theorem)。上圖 6 節點鄰接矩陣的 最大 eigenvalue: $1 \le \lambda_{max} \le 3$. 所有的 eigenvalues: (2.54, 1.08, 0.26, -0.54, -1.2, -2.13), 總和 0 (=trace).
-
一般無向圖比較少提自環 (self-loop, i loop to i), 所以 trace = 0。eigenvalues 和為 0. 所以其他的 eigenvalue 存在負數。這和 Laplacian matrix 的 eigenvalues $\ge 0$ 不同。
無向圖的 Laplacian matrix $L$ 也是對稱 matrix,Trace = 2 *|E| > 0,row vectors = 0,所以:
- 所有 eigenvalues (稱為 spectrum) 都是正實數。最小的 eigenvalue = 0, 對應的 eigenvector = [1, .., 1]’. (可以直接驗證)
- $\lambda_{n−1} \ge …\ge \lambda_{1} \ge \lambda_{0}=0$ 下圖的 Laplacian eigenvalues: (4.89, 3.70, 3, 1.68, 0.72, 0), 總和 14 (=trace).
- [1,1,…,1]’ 對應 $Ax=\lambda_0 x$ where $\lambda_0=0$.
- 比較有意思的是 $\lambda_1$ 對應最少 cut 的 graph partition. 如果 $\lambda_1=0$ 代表 graph 有不連通的 subgraph.
- 如果兩個 subgraphs 不連通,Laplacian $\lambda_1 = \lambda_0 =0$。兩個 subgraphs 對應的 eigen-vectors [111100] 和 [000011] 對應兩個 0 eigenvalues. 依次類推多個不連通 subgraphs.
- 因為 minimize yLy’, where y = (1, 1, .. -1, -1)? (To be checked!)

有向圖的特徵值 Directed Graph’s Eigenvalue
有向圖 (directed graph) 的鄰接矩陣 $A$ 一般是非對稱矩陣且 Trace $\ge$ 0,如下圖的三個例子
- 非對稱矩陣的 eigenvalues 不一定是實數。但非對稱鄰接矩陣所有 elements 都是正值,仍然適用 Perron-Frobenius theorem.
- 最大的 eigenvalue 是實數,介於最大和最小的 degree 之間。其對應的 eigenvector 可以全為正值。
- eigenvalue 總和 = trace.
- 下圖的三個 adjacency matrix A, B, C 的 eigenvalue $1 \le \lambda_{max} \le 2$.
- A 的 eigenvalues (1.62, -0.62), 總和 1.
- B 的 eigenvalues (1.62, 0.5+0.87i, 0.5-0.87i, -0.62), 總和 2.
- C 的 eigenvalues (1.62, -0.5+0.87i, -0.5-0.87i, -0.62), 總和 0.
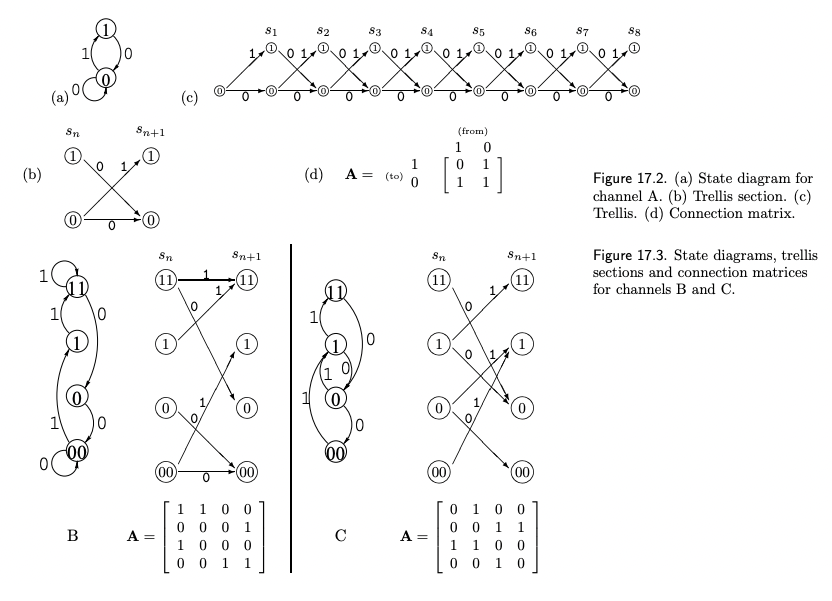
- 有向圖比較少但可以定義 Laplacian matrix。分成 in-degree Laplacian 和 out-degree Laplacian, 見下圖。
- Out-degree 是每個節點的 out-link 數目,所以 Out-Degree Laplacian 的 row vector 為 0。
- In-degree 是每個節點的 in-links 數目,所以 In-Degree Laplacian 的 column vector 為 0。
- 一定有 eigenvalue = 0, 但和無向圖的 Laplacian 一樣特性嗎? probably not, TBC.
- 下例:
- 鄰接矩陣的 eigenvalues (1.32, -0.66+0.56i, -0.66-0.56i), 總和 0.
- Out-degree Laplacian 的 eigenvalues (2, 2, 0), 總和 4.
- In-degree Laplacian 的 eigenvalues (2, 2, 0), 總和 4. 和 out-degree 一樣。
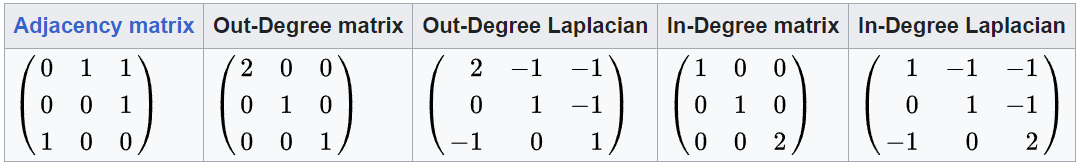
權重圖和權重矩陣 Weight Matrix Vs. Adjacency Matrix
| 我們可以延伸 graph $G(V, E)$ 的定義從 (hard) edge (邊), $E = {(v_i, v_j) | a_{ij} \in 0, 1}$; 變成 (soft) link (連結), $E = {(v_i, v_j) | w_{ij} \ge 0 }$. (Continuous or discrete) weights 擴大了 graph 的應用! |
-
$V = {v_i}$ 是頂點的集合。$ V = n$ 代表節點數目,相當 graph 的大小。 -
$W \in \R^{n\times n}$ 稱爲權重矩陣:$w_{ij} = \begin{cases} w_{ij} \ge 0 & \text{ if } i \neq j \ 0 & \text{ else } i = j \end{cases}$
-
如果 $w_{ij} \in {0, 1}$, $W = A$ 權重矩陣化簡成鄰接矩陣。
-
此時自然需要修正頂點的度 (degree of a vertex) 的定義和 Degree matrix.
-
$d(v_i) = \sum_{j=1}^n w_{ij}$ degree of $v_i$
-
$D = D(G) = diag( d(v_1), d(v_2), …, d(v_n))$
-
-
Laplacian matrix 需要被修改 $L = D - A \to L = D - W$, 基本特性都一樣!
- 所有 eigenvalues 都是正實數:$\lambda_{n−1} \ge …\ge \lambda_{1} \ge \lambda_{0}=0$. 最小的 eigenvalue $\lambda_0 = 0$, 對應的 eigenvector = $u_0 = [1, .., 1]^T$, i.e. $L \mathbf{1}^T = \mathbf{0} $
- $x^T L x = \frac{1}{2}\sum_{i,j} w_{ij} (x_i - x_j)^2 \ge 0$
| 此外我們定義更多的東西,記得之前 $tr(D) = tr(L) = \sum_{i=1}^n d(v_i) = \sum_{i=1}^n \sum_{j=1}^n a_{ij} = 2 | E | $, 現在改成體積! |
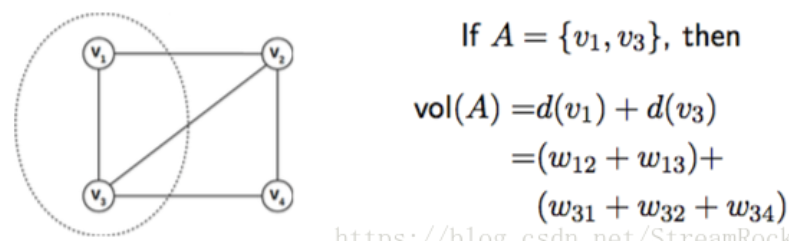
- Volume:對於 $V$ 的 subset $A, A \subseteq V$, 定義 $A$ 的 volume (體積)
- $vol(A) = \sum_{v_i \in A} d(v_i) = \sum_{v_i \in A} \sum_{j=1}^n w_{ij}$
- 如果 $A = V$, $vol(V) = \sum_{i=1}^n d(v_i) = tr(D) = tr(L) = \sum_{i=1}^n \sum_{j=1}^n w_{ij}$
-
如果 $w_{ij} = a_{ij}$, $vol(V) = 2 E $
-
- 所以 $vol(A)$ 就是部分的 trace of $D$ or $L$.
- $vol(A) = \sum_{v_i \in A} d(v_i) = \sum_{v_i \in A} \sum_{j=1}^n w_{ij}$
- Links(A, B),節點集之間的連接:Give two subsets of vertices $A, B \subseteq V$. 定義 $links(A, B) = \sum_{v_i \in A, v_j \in B} w_{ij}$
- A and B 不一定是互斥
- 因爲 $w_{ij} = w_{ji}$, $W$ 是 symmetric matrix, 所以 $links(A, B) = links(B, A)$
- $vol(A) = links(A, V) = \sum_{v_i \in A, v_j \in V} w_{ij} $
- 上例 $ links(A,V) = w_{12} + w_{13} + w_{31} + w_{32} +w_{34} = vol(A)$
- Cut(A):$cut(A) = links(A, V-A)$
- 上例 $ cut(A) = links(A, V-A) = w_{12} + w_{32} + w_{34}$
- Assoc(A) : $assoc(A) = links(A, A)$
- 上例 $ assoc(A) = links(A, A) = w_{13} + w_{31}$
- $vol(A) = cut(A) + assoc(A)$
Appendix
實數對稱矩陣 or Complex Hermitian Matrix 定理
特徵值的重要定理:Courant-Fischer min-max theorem
本定理是針對複數 Hermitian matrix 或是實數矩陣, $A = A^*$ (complex matrix) or $A = A^T$ (real matrix)
實數對稱矩陣 (或複數 Hermitian matrix) 有獨特的地位:
- Eigenvalues 均爲實數,Eigenvectors 互相正交。證明很容易 $A x = A^* x = \lambda x \to x^* A = \lambda^* x^* \to x^* A x = \lambda^* x^* x \to x^* \lambda x = \lambda^* x x^* \to \lambda = \lambda^*$
-
EVD 和 SVD 基本一致,不過 eigenvalues and eigenvectors 可能差正負號。代表 invariant eigenvectors 也是正交 basis.
- $x^* A x$ : 對於任意 column vector 向量 $x \in \C$, $x^* A x$ 為實數。(這對複數 vector 很重要,對於實數 vector trivial).
- 證明:$x^* A x = x^* Q D Q^* x = z^* D z = \sum_i \lambda_i |z_i|^2 \in \R$ 因爲 $\lambda_i \in \R$
- 以 2D SVD 爲例,正交 basis 就是單位圓 vector $|x|=1$ 經過 $Ax$ mapping 後產生最大和最小的 vector. 因爲是對稱矩陣,SVD 和 EVD 一致,所以 $\lambda_{max}$ 對應最大的 $|Ax|$, 所以 $\lambda_{min}$ 對應最小的 $|Ax|$
- $\lambda_{max} = \max \frac{x^* A x}{x^* x}$
- $\lambda_{min} = \min \frac{x^* A x}{x^* x}$
- 那麽 3D, 4D 或更高維的 eigenvalues 又是如何呢?這就是 Courant-Fischer min-max theorem
Rayleigh Quotient
-
定義 Rayleigh Quotient: $R = \frac{x^* A x}{x^* x}$ where $x \ne 0$
-
Given $A$ 是 $n \times n$ 的 Hermitian matrix (or real symmetric matrix), eigenvalues 皆爲實數。假設 $\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_n$, 對應的正交 eigenvectors 為 $u_1, u_2, …, u_n$則有
- $\max R = \max \frac{x^* A x}{x^* x} = \lambda_1$ when $x = k u_1$
- $\min R = \min \frac{x^* A x}{x^* x} = \lambda_n$ when $x = k u_n$
-
證明:$R = \frac{x^* A x}{x^* x} = \frac{x^* Q D Q^* x}{x^* x} = \frac{z^* D z}{z^* z} = \frac{\sum_i \lambda_i z_i ^2 }{\sum_i z_i }$ 因此 $ \lambda_n \le R \le \lambda_1$ - $z = Q^* x$ 並且 $x^* x = z^* z$
-
直觀看出如果是和 $u_1$ 正交的空間 $(0, u_2, …, u_n )$ 的 Rayleigh Quotient 最大值是 $\lambda_2$, i.e.
-
$\max_{x \perp u_1} \frac{x^* A x}{x^* x} = \max_{x \in (u_2, .. u_n)} \frac{x^* A x}{x^* x} = \lambda_2$
- 同樣的邏輯,$\max_{x \in (u_k, .. u_n)} \frac{x^* A x}{x^* x} = \lambda_k$
- 比較有趣是,最後 eigenvalue $\max_{x \in (u_n)} \frac{x^* A x}{x^* x} = \lambda_n = \min_{x} \frac{x^* A x}{x^* x}$
-
上式必須知道 $u_1$ 是否有方法繞過 $u_1$? Yes, 利用 min
-
考慮任意向量 $w \in \C$ 且 $x \perp w \to z \perp Q^* w$, 令 $V = {z z\perp Q^* w}$, 且 $V’ = {z z\perp Q^* w, z_3 = z_4 … = z_n =0}$, 則有 $V’ \subset V$ - $\max_{x \perp w} \frac{x^* A x}{x^* x} = \max_{z \perp Q^* w} \frac{z^* D z}{z^* z} = \max_{z \in V} \frac{z^* D z}{z^* z}$ $ \ge \max_{z \in V’} \frac{z^* D z}{z^* z} = \max_{z \in V’} \frac{\lambda_1 |z_1|^2 + \lambda_2 |z_2|^2}{|z_1|^2 + |z_2|^2} \ge \lambda_2$
- 等號成立當 $w = u_1$
-
-
因此 $\min_w \max_{x \perp w} \frac{x^* A x}{x^* x} = \lambda_2$
- 這公式有點難看懂。就是任意的 (n-1) 維子空間,所有最大值中的最小值是 $\lambda_2$. 仔細想一下,如果 $w \nparallel u_1$, (n-1) 維子空間一定包含 $u_1$, R 的最大值是 $\lambda_1$; 只有當 $w \parallel u_1$, (n-1) 維子空間不包含 $u_1$, R 的最大值是 $\lambda_2 \le \lambda_1$, 才是正解。因此可以用 $\min_w$ 取代 $w = u_1$.
-
反過來 $\max_w \min_{x \perp w} \frac{x^* A x}{x^* x} = \lambda_{n-1}$
- 就是任意的 (n-1) 維子空間,所有最小值中的最大值是 $\lambda_{n-1}$. 仔細想一下,如果 $w \nparallel u_n$, (n-1) 維子空間一定包含 $u_n$, R 的最小值是 $\lambda_n$; 只有當 $w \parallel u_n$, (n-1) 維子空間不包含 $u_n$, R 的最小值是 $\lambda_{n-1} \ge \lambda_n$. 因此可以用 $\max_w$ 取代 $w = u_n$.
-
同樣 $\min_{w_1, w_2} \max_{x \perp w_1, w_2} \frac{x^* A x}{x^* x} = \lambda_3$
- 就是任意的 (n-2) 維子空間,所有最大值中的最小值是 $\lambda_3$. 如果 (n-2) 維子空間包含 $u_1$ 或 $u_2$, R 的最大值是 $\lambda_1$ 或 $\lambda_2$; 只有當 (n-2) 維子空間不包含 $u_1, u_2$, R 的最大值是 $\lambda_3 \le \lambda_1, \lambda_2$, 才是正解。因此可以用 $\min_{w_1, w_2}$ 取代 $w_1 = u_1, w_2 = u_2$.
-
反過來 $\max_{w_1, w_2} \min_{x \perp w_1,w_2} \frac{x^* A x}{x^* x} = \lambda_{n-2}$
-
Courant-Fischer Min-Max Theorem Summary
對於 $n \times n$ 的 Hermitian matrix (或是實數的對稱矩陣):
$\lambda_k$ 是 $k$-th 大的 eigenvalue, i.e. $\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_n$
- $\lambda_k = \min_{dim(V)=n-k+1} \max_{x \in V} R = \min_{dim(V)=n-k+1} \max_{x \in V} \frac{x^* A x}{x^* x}$
- $\lambda_k = \max_{dim(V)=k} \min_{x \in V} R = \max_{dim(V)=k} \min_{x \in V} \frac{x^* A x}{x^* x}$
經典應用 1: Wely Theorem
對於兩個 $n \times n$ 的 Hermitian matrix (or real symmetric matrix) $A$ and $B$:
\(\lambda_k(A) + \lambda_n(B) \le \lambda_k (A+B) \le \lambda_k(A) + \lambda_1(B)\) 有用的結論
-
兩個 Hermitian matrixes 的 eigenvalues 範圍
-
一個 Hermitian matrix 加上一個 semi-definite matrix (所有 eigenvalues 大於等於 0), eigenvalues 必增大
經典應用 2: Wely Theorem
對於兩個 $n \times n$ 的 Hermitian matrix (or real symmetric matrix) $A$ and $B$:
\(\lambda_k(A) + \lambda_n(B) \le \lambda_k (A+B) \le \lambda_k(A) + \lambda_1(B)\) 有用的結論
-
兩個 Hermitian matrixes 的 eigenvalues 範圍
-
一個 Hermitian matrix 加上一個 semi-definite matrix (所有 eigenvalues 大於等於 0), eigenvalues 必增大