Main Reference
https://arxiv.org/pdf/1503.03585.pdf : original Stanford Diffusion paper: 有點硬核,but very good!
https://lilianweng.github.io/posts/2021-07-11-diffusion-models/ : good blog article including conditional diffusion
https://mbd.baidu.com/newspage/data/landingsuper?rs=2863188546&ruk=xed99He2cfyczAP3Jws7PQ&isBdboxFrom=1&pageType=1&urlext=%7B%22cuid%22%3A%22_i-z80aLH8_cPv8Zla2higiavighaHiUgaSB8gidviKX0qqSB%22%7D&context=%7B%22nid%22%3A%22news_9102962014405338981%22,%22sourceFrom%22%3A%22bjh%22%7D : excellent article!!
https://jalammar.github.io/illustrated-stable-diffusion/ by Jay Alammar, excellent and no math!
[ICLR2023] 扩散生成模型新方法:极度简化,一步生成 - 知乎 (zhihu.com)
| [生成扩散模型漫谈(十七):构建ODE的一般步骤(下) - 科学空间 | Scientific Spaces](https://spaces.ac.cn/archives/9497) |
Introduction
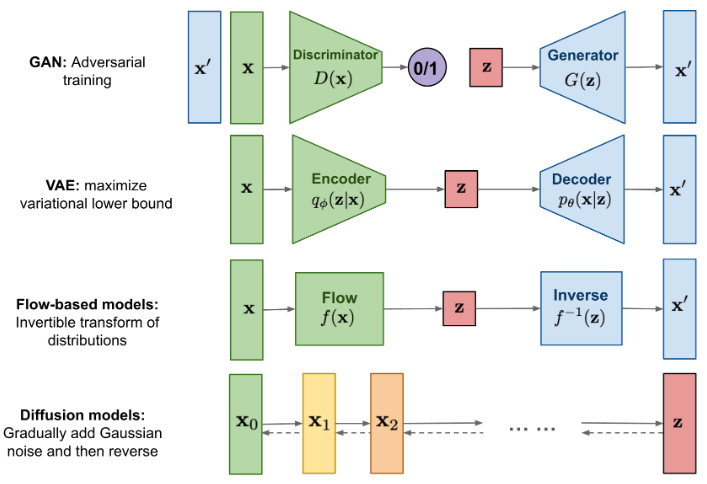
4 種常見的 image generative model. 常見的 trade-off
GAN: fast inference, but not easy to converge and strange quality
VAE: fast inference and easy train to converge, quality issue
Diffusion: easy to converge, good quality, but slow for inference
Flow-based models:
| Generative | Training | Inference | Quality |
|---|---|---|---|
| GAN | Difficult to converge | Fast | Significant percentage fail |
| VAE | Easy to converge | Fast | Blur quality |
| Flow | |||
| Diffusion | Easy to converge | Slow | Good quality |
Diffusion Misconception
我對於 diffusion model 的第一個問題是 forward path 加 Gaussian noise 會讓 entropy 增大。這應該是 non-reversible process.
為什麼可以 learning the reverse process?
learning a noise predictor? 這有點顛覆三觀,特別對於通訊背景的同學!
Ref 提供這樣的 insight: forward path 要保持在 non-equilibrium process (by time step), 才有機會 learning back.
Diffusion Path
- probability (Bayesian)
- Entropy
前文討論 diffusion model, 如何從 VAE 演變而來。
Diffusion model 有三條路:(1) denoise; (2) noise prediction; (3) score function reduction?
learning a noise predictor? 這有點顛覆三觀,特別對於通訊背景的同學!
Ref 提供這樣的 insight: forward path 要保持在 non-equilibrium process (by time step), 才有機會 learning back.
三種 VDM 詮釋
- Use neural network to learn original image from noisy image (denoise)
- Use neural network to learn noise from diffusion noise (non-equilibrium diffusion)
- Use neural network to learn the score function (gradient of log likelihood function) for arbitrary noise
重新思考 Diffusion : 傳輸映射
擴散數學 SDE - Stochastics Differential Equation
Stochastic Differential Equation (SDE)! The Fokker-Planck point of view

我們先定義好要解決的問題。無論是從雜訊生成圖片(generative modeling),還是將人臉轉化為貓臉 (domain transfer),都可以這樣概括成將一個分佈轉化成另一個分佈的問題:
給定從兩個分佈 $\pi_0$ 和 $\pi_1$ 中的採樣,我們希望找到一個傳輸映射 $T$ 使得,當 $Z_0 \sim \pi_0$ 時, $Z_1 = T(Z_0) \sim \pi_1$。
比如,在生成模型裡, $Z_0 \sim \pi_0$ 是高斯雜訊分佈, $\pi_1$ 是數據的分佈(比如圖片), 我們想找到一個方法,把雜訊 $Z_0$ 映射成一個服從 $\pi_1$ 的數據 $Z_1$。
在數據遷移 (domain transfer)裡, $Z_0$, $Z_1$分別是人臉和貓臉的圖片。所以這個問題是生成模型和數據遷移的統一表述。
在我們的框架下,映射 $T$ 是通過以下連續運動系統,也就是一個常微分方程(ordinary differential equation (ODE)),或者叫流模型(flow),來隱式定義的: \(\frac{d}{d t} Z_t=v\left(Z_t, t\right), \quad Z_0 \sim \pi_0, \forall t \in[0,1]\) 我們可以想像從 $\pi_0$ 裡採樣出來的 $Z_0$ 是一個粒子。它從 $t=0$ 時刻開始連續運動,在 $t$ 時刻以 $v\left(Z_t, t\right)$ 為速度。直到 $t=1$ 時刻得到 $Z_1$ 。我們希望 $Z_1$ 服從分佈 $\pi_1$ 。
這裡我們假設 $v\left(Z_t, t\right)$ 是一個神經網絡。我們的任務是從數據裡學習出 $v\left(Z_t, t\right)$ 來達到 $Z_1 \sim \pi_1$ 的目的。
走直線,走得快
除了希望 $Z_1 \sim \pi_1$, 我們還希望這個連續運動系統能夠在計算機裡快速地模擬出來。注意到,在實際計算過程中,上面的連續系統通常是用Euler法(或其變種)在離散化的時間上近似:
$Z_{t+\epsilon} = Z_t + \epsilon v(Z_t, t)$
這裡 $\epsilon$ 是一個步長參數。我們需要適當的選擇 $\epsilon$ 來平衡速度和精度: $\epsilon$ 需要足夠小來保證近似的精度,但同時小的 $\epsilon$ 意味著我們從 $\epsilon$ =0到 $\epsilon$ =1要跑很多步,速度就慢。
那麼問題來了,什麼樣的系統能最快地用Euler法來模擬呢?也就是說,什麼樣的體系能允許我們在用較大的步長 $\epsilon$ 的同時還能得到很好的精度呢?
答案是“走直線”。如下圖所示,如果粒子的運動軌跡是彎曲的,我們需要很細的離散化來得到很好的結果。如果粒子的軌跡是直線,那麼即使我們取最大的步長( $\epsilon=1$ ),只用一步走到 $\epsilon=1$ 時刻, 還是能得到正確的結果! 所以,我們希望我們學習出來的速度模型 $v$ 既能保證 $Z_1 \sim \pi_1$, 又能給出儘量直的軌跡。怎麼同時實現這兩個目的在數學上是一個非常不簡單(non-trivial) 的問題,涉及最優傳輸(optimal transport)的一些深刻理論。但是我們發現其實可以用一個非常簡單的方法來解決這個問題。
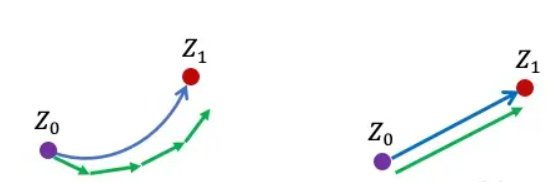
藍色:真實ODE軌跡;綠色:Euler法得到的離散軌跡。左:彎曲的運動軌跡需要較小的步長來離散化才能得到較小誤差,所以需要更多的步數;右:筆直的運動軌跡甚至可以在計算機裡用一步進行完美的模擬
Rectified Flow-基于直線ODE學習生成模型
假設我們有從兩個分佈中的採樣 $X_0 \sim \pi_0$, $X_1 \sim \pi_1$ (比如 $X_0$ 是從 $\pi_0$ 裡出來的隨機雜訊, $X_1$ 是一個隨機的數據(服從 $\pi_1$))。我們把 $X_0$ 和 $X_1$ 用一個線性插值連接起來,得到
$X_t = t X_1 + (1-t) X_0 , t \in [0, 1]$
這裡 $X_0$ 和 $X_1$ 是隨機,或者說,以任意方式配對的。你也許覺得 $X_0$ 和 $X_1$ 應該用一種有意義的方式配對好,這樣能夠得到更好的效果。我們先忽略這個問題,待會回來解決它。
現在,如果我們拿 $X_t$ 對時間 $t$求導,我們其實已經可以得到一個能夠將數據從 $X_0 \sim \pi_0$ 傳輸到 $X_1 \sim \pi_1$ 的”ODE”了, \(\frac{d}{d t} X_t= X_1 - X_0, \quad \forall t \in[0,1]\) 但是,這個”ODE”並不實用而且很奇怪,所以要打個引號:它不是一個“因果”(causal),或者“可前向模擬”(forward simulatable)的系統,因為要計算 $X_t$ 在 $t$ 時刻的速度 ($X_1 - X_0$)需要提前(在 $t<1$時)知道ODE軌跡的終點 $X_1$。如果我們都已經知道 $X_1$了,那其實也就沒有必要模擬ODE了。
那麼我們能不能學習 $v$,使得我們想要的“可前向模擬”的ODE $\frac{d}{d t} X_t= v(Z_t , t)$ 能儘可能逼近剛才這個“不可前向模擬”的過程呢?最簡單的方法就是優化 $v$ 來最小化這兩個系統的速度函數(分別是 $v$ 和 $X_1 - X_0$ )之間的平方誤差: \(\begin{aligned} & \min _v \int_0^1 \mathbb{E}_{X_0 \sim \pi_0, X_1 \sim \pi_1}\left[\left\|\left(X_1-X_0\right)-v\left(X_t, t\right)\right\|^2\right] d t, \end{aligned}\) where $X_t=t X_1 +(1-t) X_0$
這是一個標準的優化任務。我們可以將 $v$ 設置成一個神經網絡,並用隨機梯度下降或者Adam來優化,進而得到我們的可模擬ODE模型。 這就是我們的基本方法。數學上,我們可以證明這樣學出來的 $v$ 確實可以保證生成想要的分佈 $Z_1 \sim \pi_1$ 。對數學感興趣的同學可以看一看論文裡的理論推導。下面我們只用這個圖來給一些直 觀的解釋。
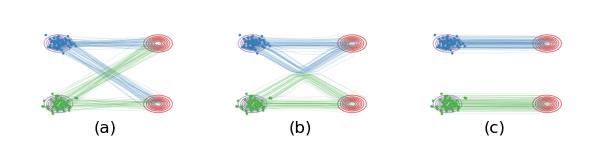
圖(a):在我們用直線連接 $X_0$ 和 $X_1$ 時,有些綫會在中間的地方相交,這是導致 $\frac{d}{d t} X_t= X_1 - X_0$ 非因果的原因(在交叉點,$X_t$ 既可以沿藍綫走,也可以沿綠綫走,因此粒子不知該向岔路的哪邊走)。
圖(b):我們學習出的ODE因為必須是因果的,所以不能出現道路相交的情況,它會在原來相交的地方把道路交換成不交叉的形式。這樣,我們學習出來的ODE仍然保留了原來的基本路徑,但是做了一個重組來避免相交的情況。這樣的結果是,圖(a)和圖(b)裡的系統在每個時刻 $t$ 的邊際分佈是一樣的,即使總體的路徑不一樣。
我們的方法起名為Rectified Flow。這裡rectified是“拉直”,“規整”的意思。我們這個框架其實也可以用來推導和解釋其他的擴散模型(如DDPM)。我們論文裡有詳細說明,這裡就不贅述了。我們現在的算法版本應該是在已知的算法空間裡最簡單的選項了。我們提供了Colab Notebook來幫助大家通過實踐來理解這個過程。

Reflow-拉直軌跡,一步生成
因為Rectified Flow要在直線軌跡的交叉點做路徑重組,所以上面的ODE模型(或者說flow)的軌跡仍然可能是彎曲的 (如上面的圖(b)),不能達到一步生成。我們提出一個“Reflow”方法,將ODE的軌跡進一步變直。
具體的做法非常簡單: 假設我們從 $\pi_0$ 裡採樣出一批 $X_0$。然後,從$X_0$ 出發,我們模擬上面學出的 flow (叫它1-Rectified Flow),得到 $X_1=\text{Flow}_1(X_0)$ 。我們用這樣得到的 ($X_0, X_1$) 對來學一個新的”2-Rectified Flow”:
\(\begin{aligned} & \min _v \int_0^1 \mathbb{E}_{X_0 \sim \pi_0, X_1 = \text{Flow}_1 (X_0)}\left[\left\|\left(X_1-X_0\right)-v\left(X_t, t\right)\right\|^2\right] d t, \end{aligned}\) where $X_t=t X_1 +(1-t) X_0$
這裡,2-Rectified Flow和1-Rectified Flow在訓練過程中唯一的區別就是數據配對不同:在1-Rectified Flow中, $X_0$與 $X_1$是隨機或者任意配對的;在2-Rectified Flow中, $X_0$與 $X_1$是通過1-Rectified Flow配對的。上面的動圖中,圖(c)展示了Reflow的效果。因為從1-Rectified Flow裡出來的 ($X_0, X_1$) 已經有很好的配對, 他們的直線插值交叉數減少,所以2-Rectified Flow的軌跡也就(比起1-Rectified Flow)變得很直了(雖然仔細看還不完美)。理論上,我們可以重複Reflow多次,從而得到3-Rectified Flow, 4-Rectified Flow… 我們可以證明這個過程其實是在單調地減小最優傳輸理論中的傳輸代價(transport cost),而且最終收斂到完全直的狀態。當然,實際中,因為每次 $v$ 優化得不完美,多次Reflow會積累誤差,所以我們不建議做太多次的Reflow。幸運的是,在我們的實驗中,我們發現對生成圖片和很多我們感興趣的問題而言,像上面的圖(c)一樣,1次Reflow已經可以得到非常直的軌跡了,配合蒸餾足夠達到一步生成的效果了。
Reflow與Distillation
給定一個配對 ($X_0, X_1$) ,要想實現一步生成,也就是 $X_1 \approx X_0 + v(X_0, 0)$, 我們好像也可以通過優化下面的平方誤差來直接”蒸餾(distillation)”出一個一步模型: \(\begin{aligned}& \min_v \mathbb{E}\left[\left\|\left(X_1-X_0\right)-v\left(X_0, 0\right)\right\|^2\right] \end{aligned}\) 這個目標函數和上面的Reflow的目標函數很像,只是把所有的時間 $t$ 都設成 $t=0$ 了。
| 儘管如此,Distillation和Reflow是有本質的區別的。Distillation試圖一五一十地復現 ($X_0, X_1$) 配對的關係。但是,如果 ($X_0, X_1$) 的配對是隨機的,Distillation最多只能得到 $X_1$ 在給定 $X_0$ 時的條件平均,也就是 $\mathbb{E}[X_1 | X_0] \approx X_0 + v(X_0, 0)$ ,並不能成功地完全匹配 $Z_1 \sim \pi_1$。即使 ($X_0, X_1$) 有確定的一一對應關係,他們的配對關係也可能很複雜,導致直接蒸餾很困難。 |
Reflow解決了Distillation的這些困難。它的意義在於 :
1) 給定任何 ($X_0, X_1$) 配對,就算是隨機的配對,他都能學出一個給出正確邊際分佈(marginal distribution)的flow。Reflow不會去試圖完全復現 ($X_0, X_1$) 的配對關係,而只注重於得到正確的邊際分佈。 2) 從Reflow出的ODE 裡採樣,我們還可以得到一個更好的配對 ($X_0, X’_1$) ,從而給出更好的flow。重複這個過程可以最終得到保證一步生成的直線ODE。
形象地來講,如果 ($X_0, X_1$) 太複雜,Reflow會“拒絶”完全復現 ($X_0, X_1$) ,轉而給出一個新的,更簡單的,但仍然滿足 $X’_1 \sim \pi_1$ 的配對 ($X_0, X’_1$) 。 所以,Distillation更像“模仿者”,只會機械地模仿,就算問題無解也要“硬做”。Reflow更像“創造者”,懂得變通,發現新方法來解決問題。
當然,Reflow和Distillation也可以組合使用:先用Reflow得到比較好的配對,最後再用已經很好的配對進行Distillation 。我們在論文裡發現,這個結合的策略確實有用。
下面,我們進一步基于具體例子解釋一下Reflow對配對的提高效果。如果一個配對 ($X_0, X_1$) 是好的,那麼從這個配對裡隨機產生的兩條直線 $X_t=t X_1 +(1-t) X_0$ 就不會相交。在我們的論文裡,這種直線不相交的配對我們叫做”Straight Coupling”。我們的Reflow過程就是在不停地降低這個相交概率的過程。下圖我們展示隨著Reflow的不斷進行,配對的直線交叉數確實逐漸降低。在圖中,對每種配對方法,我們隨機選擇兩個配對,分別用直線段連接它們,然後若它們相交,就用紅色點標出這兩條直線段的交點。 對於這種交叉的配對,Reflow就有可能改善它們。我們重複10000次並統計交叉的概率。我們發現:(1)每次Reflow都降低了交叉的概率和L2傳輸代價(2)即使2-Rectified Flow在肉眼觀察時已經很直,但它的交叉概率仍不為0,更多的Reflow次數就可能進一步使它變直並降低傳輸代價。相比之下,單純的蒸餾是不能改善配對的,這是Reflow與蒸餾的本質區別。
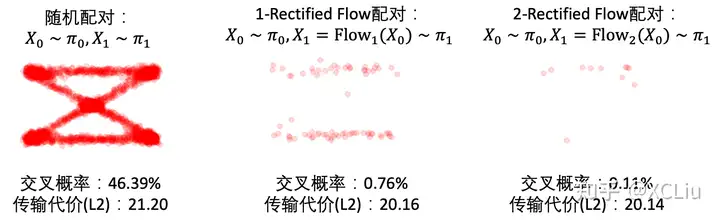
圖中,每個紅點代表一次兩隨機的直線交叉的事件。隨著reflow,交叉的概率逐漸降低,對應的ODE的軌跡也越來越直。
理論保證
Rectified Flow不僅簡潔,而且在理論上也有很好的性質。我們在此給出一些理論保證的非正式表述,如果大家對理論部分感興趣,歡迎大家閲讀我們文章的細節。
- 邊際分佈不變:當 $v$ 取得最優值時,對任意時間 $t$,我們有 $Z_t$和 $X_t$的分佈相等。因為 $X_0 \sim \pi_0, X_1 \sim \pi_1$,因此 $Z$ 確實可以將 $\pi_0$ 轉移到 $\pi_1$。
- 降低傳輸損失:每次Reflow都可以降低兩個分佈之間的傳輸代價。特別的,Reflow並不優化一個特定的損失函數,而是同時優化所有的凸損失函數。
- 拉直ODE軌跡:通過不停重複Reflow,ODE軌跡的直線性(Straightness)以 $O(1/k)$ 的速率下降,這裡, $k$ 是reflow的次數。
實驗結果-Rectified Flow能做到什麼?
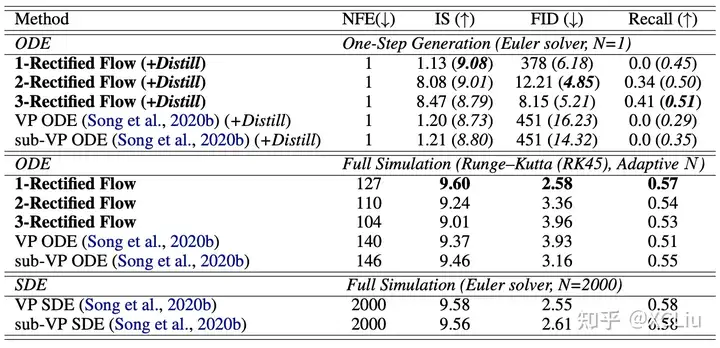
CIFAR-10實驗結果
- 使用Runge Kutta-45求解器,1-Rectified Flow在CIFAR10上得到 IS=9.6, FID=2.58,recall=0.57,基本與之前的VP SDE/sub-VP SDE[2]相同,但是平均只需要127步進行模擬。
- Reflow可以使ODE 軌跡變直,因此2-Rectified Flow和3-Rectified Flow在僅用一步(N=1)時也可以有效的生成圖片(FID=12.21/8.15)。
- Reflow可以降低傳輸損失,因此在進行蒸餾時會得到更好的表現。用2-Rectified Flow+蒸餾,我們在僅用一步生成時得到了FID=4.85,遠超之前最好的僅基于蒸餾/基于GAN loss的快速擴散式生成模型(當用一步採樣時FID=8.91) 。同時,比起GAN,Rectified Flow+蒸餾有更好的多樣性(recall>0.5)。
我們的方法也可以用於高清圖片生成或無監督圖象轉換。

1-rectified flow: 256分辨率圖象生成

1-rectified flow: 256分辨率無監督圖象轉換
同期相關工作
有意思的是,今年ICLR在openreview上出現了好幾篇投稿論文提出了類似的想法。
(1) Flow Matching for Generative Modeling
(2) Building Normalizing Flows with Stochastic Interpolants
(3) Iterative -alpha (de)Blending: Learning a Deterministic Mapping Between Arbitrary Densities
(4) Action Matching: A Variational Method for Learning Stochastic Dynamics from Samples
這些工作都或多或少地提出了用擬合插值過程來構建生成式ODE模型的方法。除此之外,我們的工作還闡明了這個路徑相交重組的直觀解釋和最優傳輸的內在聯繫,提出了Reflow算法,實現了一步生成,建立了比較完善的理論基礎。大家不約而同地在一個地方發力,說明這個方法的出現是有很大的必然性的。因為它的簡單形式和很好的效果,相信以後有很大的潛力。