Attention Is All You Need

Posted on | In

我想用 matrix math 澄清一些觀念

A: m x n

B: n x p

A B = m x n . n x p = m x p highest rank 是 min(m, n, p)

Fully Connected

Reduce Dimension (1024->100): 例如 Computer Vision 分類問題 (最後幾層 mixed spatial and channel features)

A. 先考慮 1D case, Input 是 fixed (spatial) length (1024), Output 是 fixed category (100), feature size = 1

  • Input: 1024x1; Output 100x1; Weight: 100x1024 (非常自然!)

  • Output (100x1) = Weight (100x1024) * Input (1024x1) => 1D vector = 2D matrix * 1D vector => rank ~ 100
  • 不再贅述：或是 Input’ (1x1024) * Weight’ (1024x100) = Output’ (1x100)
  • Input 是隨 content 變動的；Weights 是 trainable, 但是 train 完就 freeze; output 當然是隨 content 變動的

B. 1D case with input/output feature size 64. Input 是 (1024x64), Output (100x64), feature size = 64

  • Input: 1024x64; Output 100x64; 這時的 Weight 是什麼???
  • Output (100x64) = Weight (100x64)x(1024x64) * Input (1024x64) => 2D array = 4D tensor(!!!) * 2D array => rank ???
    • (4D) fully connected (mixed) inter-inputs and intra-input (features) weights: 100x64 x1024x64 = input x output x (feature^2) = 419M! 所有的 inter-input 和 features 之間任意 mix! 非常大的 trainable weights and computations! 不實際
    • 簡化 I：Only inter-inputs fully connected (mixed) weight, NO intra-input (feature) mix => weights 還是 100 x 1024 (x64?)! 所有的 feature 都 share 相同 weight.
    • 簡化 II (NOT applicable in this case) : Only intra-input (features) fully connected (mixed) weight, NO inter-inputs mix. 就是 intra-input features 之間 mix, 而沒有 inter-inputs mix => weights 是 64x64! 所有的 input samples share 同樣的 weighs.
      • 其實這就是 1x1 convolution! 所以這個操作也稱為 1x1 convolution!
      • Convolution 的 input 和 output size 要相同！(最多差一個 padding). 對於 1x1 convolution, 不需要 padding, input = output dimension!
      • 如果要改變 input and output size 除非再做 upsampling/downsampling!
      • 1x1 convolution 在這個 case 無法使用，因為 input samples (1024) $\ne$ output samples (100)!
    • (Caveat) 對於 transformer model: input sample 之間的 mix weights, 是由 attention block 達成！ Feature 之間的 mix, 是從 MLP 1x1 convolution 達成！見下面。
  • Input 是隨 content 變動的；Weights 是 trainable, 但是 train 完就 freeze; output 當然是隨 content 變動的

I/O Same Dimension (512->512): 生成式問題 (e.g. transformer encoder/decoder)

A. 先考慮 1D case, Input (token) 是 fixed length (512), Output (token) 是 fixed length (512), token embedding feature = 1

  • Input: 512x1; Output 512x1; Weight: 512x512
  • Output (512x1) = Weight (512x512) * Input (512x1)
    • **實務上 NLP 的 input and output length 是變動的!!, CV 一般是固定的 **
    • 所以才會有 attention layer 處理變動的部分, 而非用固定的 fully connected layer.
  • Input 是隨 content 變動的；Weights 是 trainable, 但是 train 完就 freeze; output 當然是隨 content 變動的

B. 1D case with input/output feature size 768! Input (token) 是 (512x768), Output (token) (512x768), token embedding feature = 768!

  • Input: 512x768; Output 512x768; 這時的 Weight 是什麼???
  • Output (512x768) = Weight (512x768)x(512x768) * Input (512x768)
    • (4D) fully connected (mixed) inter-inputs and intra-input (features) weights: 512x768 x512x768 = (token* feature)^2 = 155B! 所有的 inter-input 和 features 之間任意 mix! 非常大的 trainable weights and computations! 不實際
    • 簡化 I (NOT applicable in this case) ：Only inter-inputs fully connected (mixed) weight, NO intra-input (feature) mix => weights 是 512 x 512 (x768?)! 只是所有的 feature 都 share 同樣的 weight.
      • 實務上 NLP 的 input and output length 是變動的!!, 固定的 512x512 weights 不實際
      • 所以才會有 attention layer 處理變動的部分, 而非用固定的 fully connected layer.
    • 簡化 II： Only intra-input (features) fully connected (mixed) weight, NO inter-inputs mix. 就是 intra-input features 之間 mix, 而沒有 inter-inputs mix => weights 是 768x768! 所有的 input samples share 同樣的 weighs.
      • 其實這就是 convolution! 所以這個操作也稱為 1x1 convolution! Convolution 的 input 和 output 基本要相同！(最多差一個 padding). 對於 1x1 convolution, 不需要 padding, input = output dimension! 除非再做 upsampling/downsampling!
    • (Caveat) 對於 transformer model: input sample 之間的 mix weights, 是由 attention block 達成！ Feature 之間的 mix, 是從 MLP 1x1 convolution 達成！
  • Input 是隨 content 變動的；Weights 是 trainable, 但是 train 完就 freeze; output 當然是隨 content 變動的

Multi-Layer Perceptron (MLP)

  • 多半是 $\ge$ 2 layers, 如果只有 1 layer 基本就是 fully-connected layer
  • 第一層稱為 hidden layer, node 數目多半大於或等於 input node. 可能 2 倍。
  • 第二層如果是 output layer, node 數目一般小於 input node for 分類問題。等於 input for transformer token.
  • 在 computer vision application, 多半是放在最後部分。feature size 已經被打包成 1.
    • 例如: 1024x1 (input feature layer) -> 2048x1 (hidden layer) -> 100x1 (output)

(Kernel) Convolution layer

Convolution 其實蠻奇葩的。看起來像是 matrix multiplication. 但如果真的用 GEMM 做 convolution, 例如 GPU, 則會發生非常低的 utilization rate!! 這和 fully-connected layer 完全不同！

**為什麼 GEMM 會有非常低的 utilization rate? **

  1. 因為把 convolution 變成 matrix multiplication, 會得到 sparse matrix! 特別是 kernel 非常小 (e.g. 3x3) 的情況下。
  2. Kernel matrix 都是重複的 pattern
  • 1D: Input: 256 x 1, Kernel: 3 x 1
  • Kernel appends to Kernel matrix : 3 x1 => 256 x 258. (258 = 256 + 3 -1), 其中非 0 只有 3 x 258, 其他為 0. 另外非 0 的 258 列又是重複 pattern!!
  • Output (258x1) = Expanded Kernel (258x256) * Input (256x1)

B. 假如 feature (channel-in, Cin) size 是 64

  • 1D input + 1D channel: Input: 256 x 64, Kernel: 3 x 64

  • Kernel appends to Kernel matrix : 3 x 64 => 256 x 258 x 64, 其中非 0 只有 3 x 258, 其他為 0. 另外非 0 的 258 列是重複 pattern!!

  • Output (258x64) = Expanded Kernel (258x64)x(256x64) * Input (256x64)
    • (4D) fully connected (mixed) inter-inputs and intra-input (channel features) weights: (258x64) x (256x64)! 所有的 inter-input 和 features 之間任意 mix! 不過因為 kernel matrix 大多是 0, 只有對角線附近的元素 (kernel size, e.g., 3) 非 0 且重複，也就是 inter-input 只限制在 kernel size 的 mix. 所以 kernel weight parameters = (1(重複)x64) x (3(kernel 非0)x64) = 3 x 64 x 64! 就是 trainable parameters = 3 x 64 x 64. 也就是 kernel * Cin * Cout
    • 簡化 I (depth-wise convolution)：Only inter-inputs fully connected (mixed) weight, NO channel feature mix => weights 是 1(重複)x3(kernel)x64! 只是所有的 channel feature 都 share 同樣的 weight.
    • 簡化 II (point-wise convolution)：Only channel features fully connected (mixed) weight, NO inter-inputs mix. 就是 1x1 convolution. Channel features 之間 mix, 而沒有 inter-inputs mix => weights 是 64x64=Cin x Cout! 所有的 input samples share 同樣的 weighs.
      • 這裡有一個 twist, 就是 output channel features 不一定要和 input channel feature 一樣, Cin x Cout！
  • Input 是隨 content 變動的；Weights 是 trainable, 但是 train 完就 freeze; output 當然是隨 content 變動的

C. 假如 feature (2D input + channel-in, Cin) size 是 64

  • 2D input + 1D Channel: Input: 256 x 256 x 64, Kernel: 3 x 3 x 64
  • Kernel appends to Kernel tensor? : 3 x 3 x 64 => (256x258) x (256x258) x 64, 其中非 0 只有 3 x 3 x 258 x 258, 其他為 0. 另外非 0 的 258 列是重複 pattern!!
  • Output (258x258x64) = Expanded Kernel (258x258x64)x(256x256x64) * Input (256x256x64)
    • (4D) fully connected (mixed) inter-inputs and intra-input (channel features) weights: (258x64) x (256x64)! 所有的 inter-input 和 features 之間任意 mix! 不過因為 kernel matrix 大多是 0, 只有對角線附近的元素 (kernel size, e.g., 3x3) 非 0 且重複，也就是 inter-input 只限制在 kernel size 的 mix. 所以 kernel weight parameters = (1x1(重複)x64) x (3x3(kernel 非0)x64) = 3 x 3 x 64 x 64! 就是 trainable parameters = 3 x 3 x 64 x 64. 也就是 kernel * Cin * Cout
    • 簡化 I (depth-wise convolution)：Only inter-inputs fully connected (mixed) weight, NO channel feature mix => weights 是 3x3(kernel)x64! 只是所有的 channel feature 都 share 同樣的 weight.
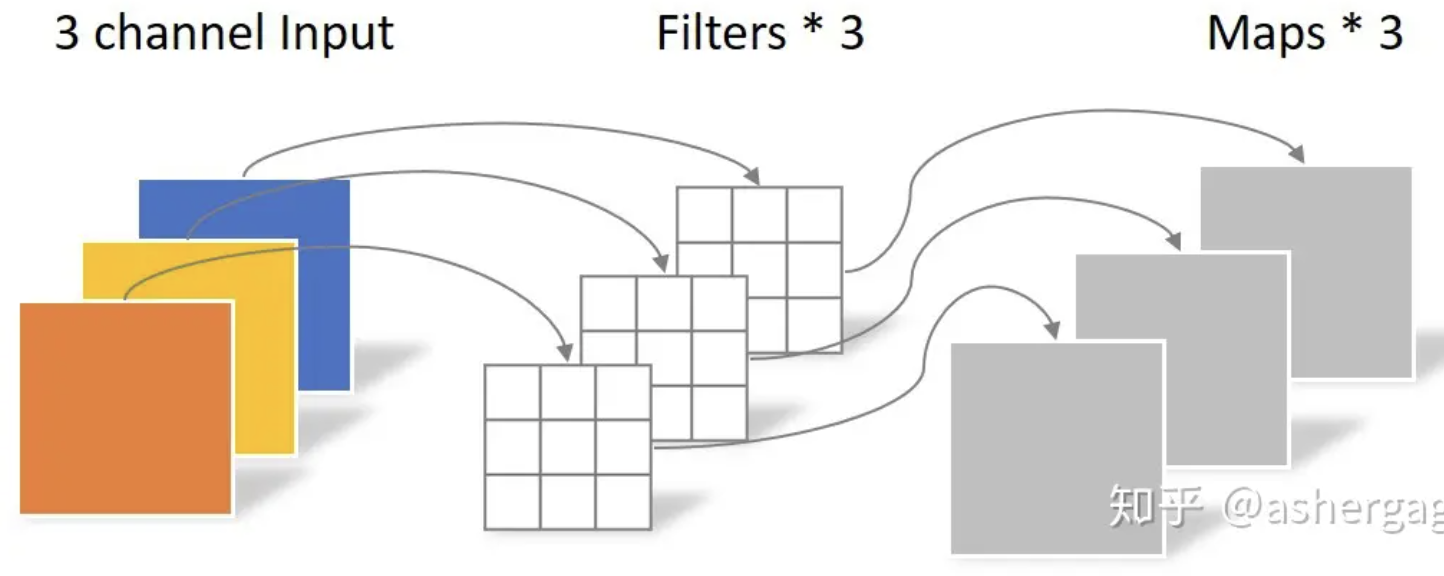
    • image-20230404143946684
    • 簡化 II (point-wise convolution)：Only channel features fully connected (mixed) weight, NO inter-inputs mix. 就是 1x1 convolution. Channel features 之間 mix, 而沒有 inter-inputs mix => weights 是 64x64=Cin x Cout! 所有的 input samples share 同樣的 weighs.
      • 這裡有一個 twist, 就是 output channel features 不一定要和 input channel feature 一樣, Cin x Cout！
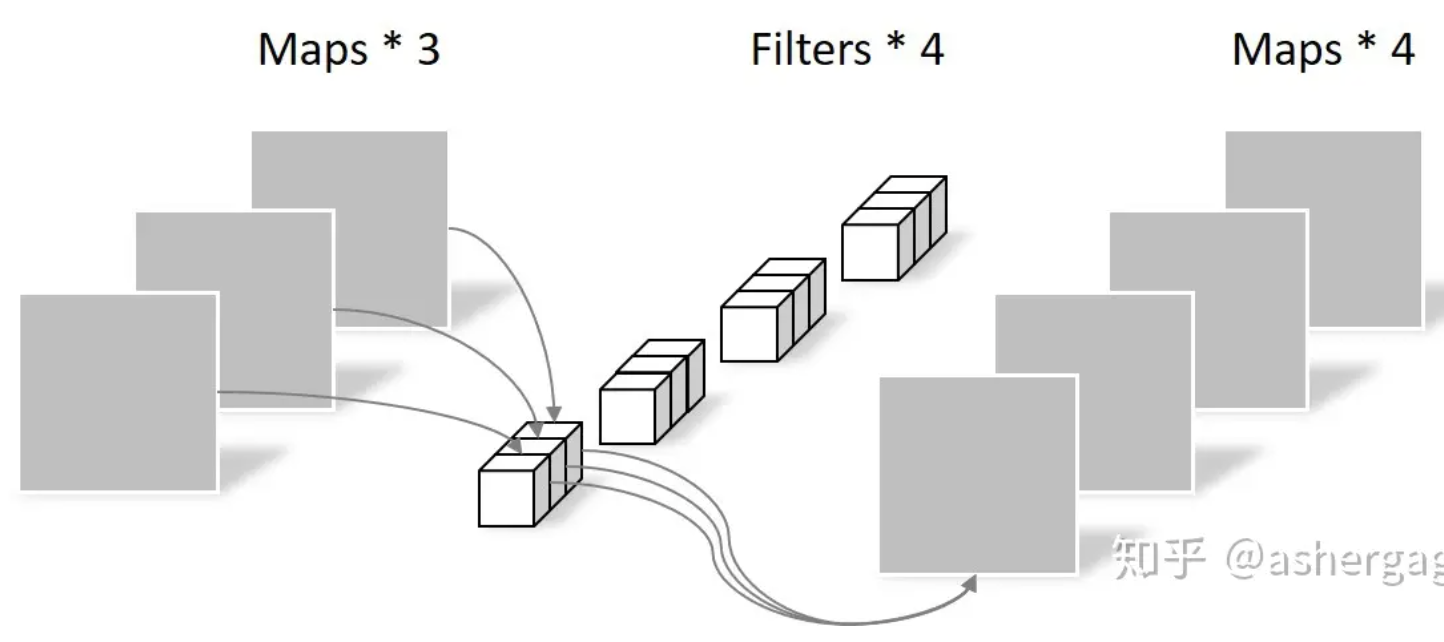
      • image-20230404144103664
  • 原來的 kernel size x Cin x Cout (full convolution) 變成 kernel size x Cin (depth-wise) + Cin x Cout (point-wise).
    • 3x3x64x64 = 36.9K > 3x3x64x1 + 1x1x64x64 = 4.7K
  • Input 是隨 content 變動的；Weights 是 trainable, 但是 train 完就 freeze; output 當然是隨 content 變動的

Convolution 雖然實際計算不會用 matrix multiplication. 當做理論用還是 OK.

Concatenate (Matrix Representation), Cout dimension!

Slice

Attention is all you need

NLP 的問題是 input text string 一般是變動的，例如：“Hello, world”, 或是 “This is a test of natural language processing!”

Input 是 text string, 切成 tokens ($\le$512). 儘量塞 sentence 或是 0 padding. 每個 token 是 768-dim (feature) vector. 也就是 (input) token embedding 是一個 arbitrary width ($\le$ 512) 2D matrix X. 最終希望做完 attention 運算還是得到同樣的 shape.

先看不好的方法 for Natural Language Porcessing

  • 如果 input-output 是 inter-token 和 inter-feature 的 fully-connected network, 顯然不可行！
    • 因為是一個 $(512\cdot 768)^2 = 154$ B weights，同時 computation 也要 154 T operation!
    • Input 是變動的長度, 所以固定的 154B weights 無法得到不同 width 的結果。

image-20230402210446588

  • 如果 input-output 只作用或處理在 embedding dimension (i.e shared weight for all input tokens!), 例如 1-dimension convolution, kernel 就是 1x768, channel length = 768. 假設 input 是 3-channel (e.g. RGB or KQV), parameter = 3 x 768^2 = 2M parameters. 顯然也不夠力。同時 each token 都是獨立處理，缺乏 temporal information!

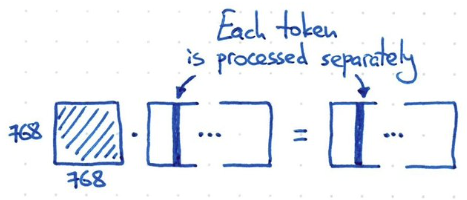
image-20230402220358950

Catch

  • 我們需要找一個方法介於 fully connected model and 1-d convolution network!!!
    • Fully connect network size: (512x768)^2 = 154B
    • 1-dimension network size: (768x768) < 1M
  • 所以需要如同下面的方法！計算 $f(X) = X X^T X$. 假設 X 是 m x n -> (m x n) (n x m) (m x n) = m x n 得到和原來一樣的 shape!
  • 此時 token 和 token 之間 interact, 但又不像 fully connected 這麼多 interaction!!! 這就是 attention 的原理！
  • Rank = min(m, n)！ 如果 width 很小，例如短句。或是 attention 範圍小。rank 就小。計算量就小，也避免 overfit!
  • 問題是以下的方法，沒有任何 trainable parameter!!!!

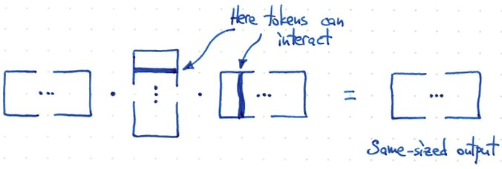
image-20230402220424409

如何引入 Trainable Parameter?

  • 如何做到？非常容易！ 重組 input 引入 V (value) matrix. 引入 K, Q matrix and similarity/attention matrix!!
  • 使用 K, Q 計算 similarity matrix (512x512)，then softmax for attention matrix. V 通過 attention matrix 得到 output!
  • 因為 attention matrix 的遠小於 768! 所以有類似 low rank 的功效。
  • V, K, Q 的 dimension:
    • V: 768x768, K: 768x768, Q: 768x768. Total: 3 x (768x768)

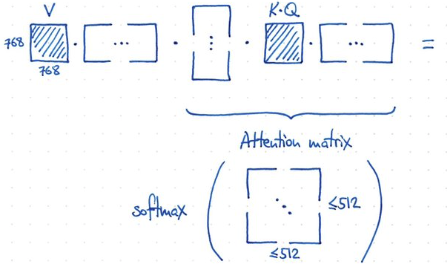
image-20230402220443383

  • 最後再加上一個 MLP layer. Hidden layer 的 dimension 是 4x768!, 所以 parameter = 768^2 x 4 x 2? = 5M parameters!

image-20230402220500305

  • 一個 transformer block 的 parameter = V,K,Q x 768^2 = 3 x 768^2 = 2M param + 5 M= 7.1 M parameters

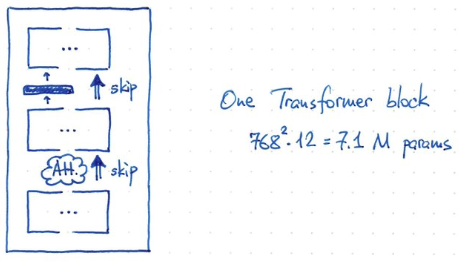
image-20230402220521798

  • BERT 有 12 blocks, giving ~ 85M params (再加上 25M for token embedding, 512 x 768 = 0.39M??)
  • GPT2 = ?

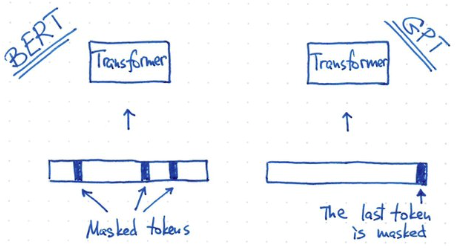
image-20230402220542789

  • BERT 和 GPT training 方式不同： BERT 使用 masked token. GPT 使用 predicted token.

Convolution is all you need

Input 大多是 256x256x3 (RGB) pixel (or 考量 data augmentation +/-16 pixel: 224x224 pixel ).

如果是 generative model, 例如 de-noise, de-blur, output 和 input dimension 一樣。

因爲不是分類問題，沒有用 fully-connected layer.

先看不好的方法 for Computer Vision

  • Fully connected trainable parameter: (256x256x3)^2 = 38B! 雖然大力出奇蹟。但這只是小圖。如果是大圖 4K x 4K, 參數增加 16 倍。基本上 fully connected network 不 scalable!
  • 如果是一次 depth-wise + point-wise trainable parameter = (256x256)^2 x 3 + 3x3 = 12.9B! 雖然比較小，還是非常大，not scalable!

可行的方法

三種方法：(1) convolution; (2) transformer; (3) hybrid.

(1) 第一種方法 convolution + hierarchy (down-sampling/up-sampling)

Kernel: 3x3, Cin = 3, Cout=64 => first layer: (shared) trainable weights = 3x3x3x64 = 1.7K!! 非常小。

  • 但是 計算量 (要掃過所有圖區域)  » trainable parameters. 就是計算量 dominate! 好處是 power efficiency 比較好，可以不用一直拿 weights.
  • Kernel 小的缺點是 receptive field 非常小。需要 down-sampling and up-sampling 增加 receptive field! 但同時增加 channel depth (feature) 避免 loss information.
    • 所以後面的 kernel trainable parameters 會增加: 3x3x512x1024 = 4.7M, 還在可控範圍！就算是 20 layers 也不過 ~80M parameters! 而且如果是 4K x 4K, parameter 是 linear 增加，而不是幾何增加！
  • 如果還要更少 trainable weights, 可以用 depth-wise + point-wise (例如 MobileNet) => 3x3x512 + 1x1x512x1024 = 529K, 大約只有 4.7M 的 11%。

(2) 第二種方法 Vision Transformer (ViT)

如果是用 3x3 pixel 為一個單位 (patch)，256x256 picture 就會有 7281 patches, 對於 transformer model 顯然太多。

ViT 使用 16x16 pixel 為一個 patch, 256x256 picture 就有 256 patches/tokens, 剛好可以給 transformer 使用！

如果一個 layer 是 7.1M parameter, 12 layers 就是 84M pixel. 好像還是在可接受範圍！

  • ViT 原理一樣！1-patch = 16x16x3 = 768 dimension. 224x224 image, 一共有 196 patches (<512 token).

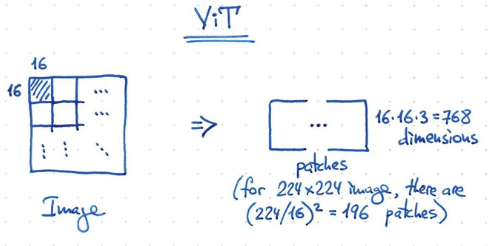
    image-20230402220606024

  • ViT 另一個簡化是使用 1-convolution 可以 work!! 也就是 shared weight!

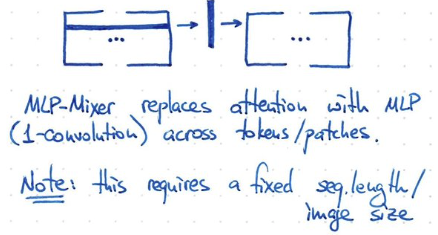
image-20230402220640057

ViT-22B

image-20230406213629587

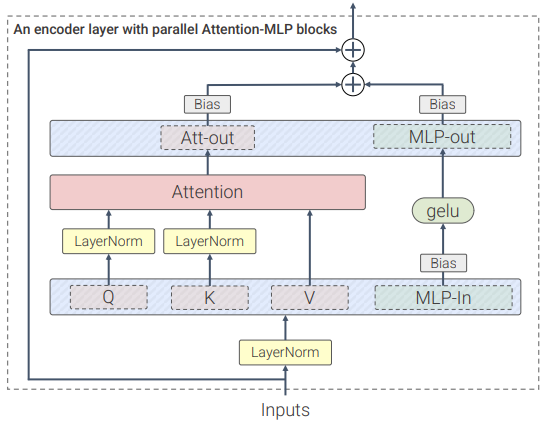
ViT-22B 是一個基于Transformer架構的模型，和原版ViT架構相比，研究人員主要做了三處修改以提升訓練效率和訓練穩定性。

並行層（parallel layers）

ViT-22B並行執行注意力塊和MLP塊，而在原版Transformer中為順序執行。

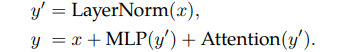
image-20230406214114945

Google 的 PaLM模型的訓練也採用了這種方法，可以將大模型的訓練速度提高15%，並且性能沒有下降。

query/key (QK) normalization

在擴展ViT的過程中，研究人員在80億參數量的模型中觀察到，在訓練幾千步之後訓練損失開始發散(divergence)，主要是由於注意力logits的數值過大引起的不穩定性，導致零熵的注意力權重（幾乎one-hot）。

為瞭解決這個問題，研究人員在點乘注意力計算之前對Query和Key使用 LayerNorm

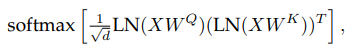
image-20230406215726984

刪除QKV 投影和 LayerNorms 上的 bias

和PaLM模型一樣，ViT-22B從QKV投影中刪除 bias，並且在所有LayerNorms中都沒有 bias 和centering，使得硬件利用率提高了3%，並且質量沒有下降。

不過與PaLM不同的是，ViT-22B對（內部和外部）MLP稠密連接層使用了 bias，可以觀察到質量得到了改善，並且速度也沒有下降。

ViT-22B的編碼器模組中，嵌入層，包括抽取patches、線性投影和額外的 position embedding 都與原始ViT中使用的相同，並且使用多頭注意力pooling來聚合每個頭中的per-token表徵。

ViT-22B的patch尺寸為14×14，圖象的分辨率為224×224（通過inception crop和隨機水平翻轉進行預處理），一共有 224x224/(14x14)=16x16=256 patches。

(3) 第三種方法 Hybrid:

convolution 對於 local feature 效果不錯。但是 transformer 對於 global feature 很好。是否可以結合？

(A) 比如前幾層是用 convolution, 之後用 transformer!

(B) 或是 convolution 的 block 直接用 transformer block 替代或 vice versa

(C) 或是把 hierarchy (down-sampling) 用在 transformer.

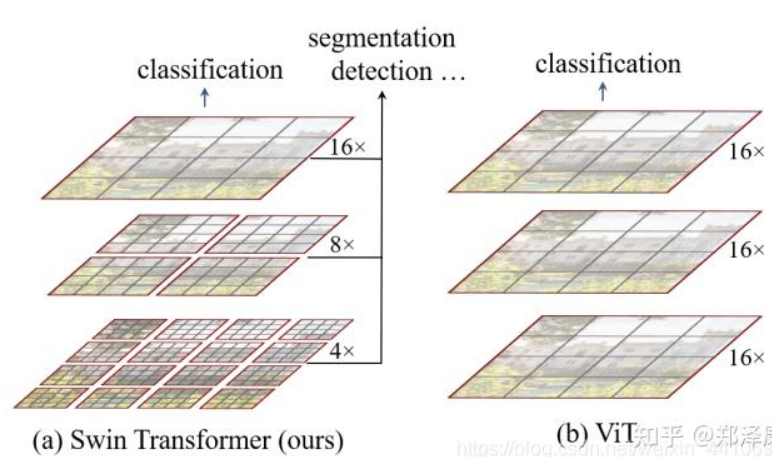
(3C) SWIN Transformer

基本是利用 CNN 的 windows (local attention) + shifted windows + patch merge + hierarchy

只是先做 attention, 再用 local attention window + shifted attention windows (類似 CNN sliding windows!)

Vision Transformer應用到圖象領域主要有兩大挑戰：

  • 視覺實體變化大，在不同場景下視覺Transformer性能未必很好
  • 圖象分辨率高，像素點多，Transformer基于全局自注意力的計算導致計算量較大

針對上述兩個問題，SWIN Transformer 提出了一種包含滑窗操作，具有”層級”設計的Swin Transformer。

其中滑窗操作包括不重疊的local window，和重疊的cross-window。將注意力計算限制在一個窗口中，一方面能引入CNN卷積操作的局部性，另一方面能節省計算量。

ViT 是 16x16 pixel/patch, 所以有 16x16 (256x256 pixels) patch.

SWIN 用更小的 pixel 為 patch, 這樣有很多的 tokens? (16倍) -> 使用更小的 (local) window attention.

Window attention + shifted window attention 取代 global attention!

用 patch merge 取代 pooling!

image-20230406221600548

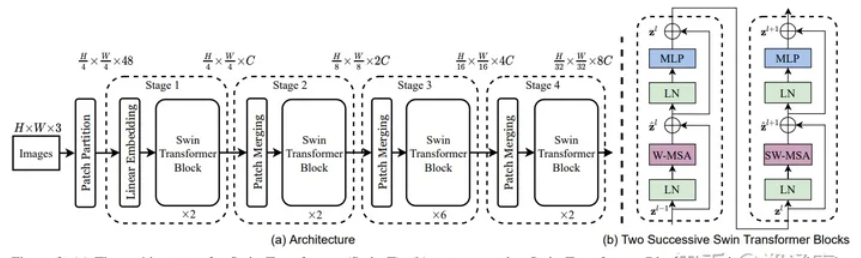
image-20230406222418591

Math and figure:

  • Input

####