LLM KV Cache Memory and BW

Source

大模型推理性能優化之KV Cache解讀 - 知乎 (zhihu.com)
The KV Cache: Memory Usage in Transformers https://www.youtube.com/watch?v=80bIUggRJf4&ab_channel=EfficientNLP
[LLM]KV cache詳解圖示，顯存，計算量分析，代碼 - 知乎 (zhihu.com)

TBD

Efficient Memory Management for Large Language Model Serving with PagedAttention (arxiv.org)
Flash Attention with attention bias: https://zhuanlan.zhihu.com/p/567167376
Flash attention 2: https://tridao.me/publications/flash2/flash2.pdf
Flash Decoder: https://princeton-nlp.github.io/flash-decoding/
詳細的 GPT2/3 參數計算: https://www.lesswrong.com/posts/3duR8CrvcHywrnhLo/how-does-gpt-3-spend-its-175b-parameters
GPT3 原始 paper.
GPT2 原始 paper.
LLM1, https://finbarr.ca/how-is-llama-cpp-possible/
FlashAttention圖解（如何加速Attention） - 知乎 (zhihu.com)
NLP（十七）：從 FlashAttention 到 PagedAttention, 如何進一步優化 Attention 性能 - 知乎 (zhihu.com)

Takeaway

KV cache 利用額外的記憶體 (DRAM or HBM) 減少 transformer 中 K, V 的計算量，同時減小 output token 的 latency.
KV cache 的副作用是: 1. 額外的記憶體; 2. 額外的記憶體頻寬
Attention block: KV cache memory management on (on-die) SRAM and the 1st memory (off-die memory).
KV cache split, KV flash, KV decode
dynamic cache

0. 引言

做大模型性能優化的一定對KV Cache不陌生，那麼我們對這個技術瞭解到什麼程度呢？請嘗試回答如下問題：

KV Cache節省了Self-Attention層中哪部分的計算？
KV Cache對MLP層的計算量有影響嗎？NO
KV Cache對block間的數據傳輸量有影響嗎？

本文打算剖析該技術並給出上面問題的答案。

1. KV Cache是啥？

大模型推理性能優化的一個常用技術是KV Cache，該技術可以在不影響任何計算精度的前提下，通過空間換時間思想，提高推理性能。網上有一些關於該技術的分析博客，但讀過後仍然會很迷糊，甚至可能會被帶偏，認爲這個Cache過程和數據庫讀取或CPU Cache加速類似的荒謬結論。剛開始我也有類似誤解，直到逐行查閱並運行源碼，才清楚瞭解到其Cache了啥，以及如何節省計算的。

2. 背景

生成式generative模型的推理過程很有特點，我們給一個輸入文本 (長度為 $s$)，模型會輸出一個回答（長度爲 $n$），其實該過程中執行了$n$ 次推理 (inference) 過程。即GPT類模型一次推理只輸出一個token，輸出token會與輸入tokens 拼接在一起，然後作爲下一次推理的輸入，這樣不斷反覆直到遇到終止符。

如上描述是我們通常認知的GPT推理過程。代碼描述如下：

import torch
from transformers import GPT2LMHeadModel, GPT2Tokenizer


model = GPT2LMHeadModel.from_pretrained("/WORK/Test/gpt", torchscript=True).eval()

# tokenizer
tokenizer = GPT2Tokenizer.from_pretrained("/WORK/Test/gpt")
in_text = "Lionel Messi is a"
in_tokens = torch.tensor(tokenizer.encode(in_text))

# inference
token_eos = torch.tensor([198]) # line break symbol
out_token = None
i = 0
with torch.no_grad():
    while out_token != token_eos:
        logits, _ = model(in_tokens)
        out_token = torch.argmax(logits[-1, :], dim=0, keepdim=True)
        in_tokens = torch.cat((in_tokens, out_token), 0)
        text = tokenizer.decode(in_tokens)
        print(f'step {i} input: {text}', flush=True)
        i += 1

out_text = tokenizer.decode(in_tokens)
print(f' Input: {in_text}')
print(f'Output: {out_text}')

輸出

step 0 input: Lionel Messi is a player
step 1 input: Lionel Messi is a player who
step 2 input: Lionel Messi is a player who has
step 3 input: Lionel Messi is a player who has been
step 4 input: Lionel Messi is a player who has been a
step 5 input: Lionel Messi is a player who has been a key
step 6 input: Lionel Messi is a player who has been a key part
step 7 input: Lionel Messi is a player who has been a key part of
step 8 input: Lionel Messi is a player who has been a key part of the
step 9 input: Lionel Messi is a player who has been a key part of the team
step 10 input: Lionel Messi is a player who has been a key part of the team's
step 11 input: Lionel Messi is a player who has been a key part of the team's success
step 12 input: Lionel Messi is a player who has been a key part of the team's success.
step 13 input: Lionel Messi is a player who has been a key part of the team's success.

 Input: Lionel Messi is a
Output: Lionel Messi is a player who has been a key part of the team's success.

可以看出如上計算的問題嗎？每次推理過程的輸入tokens都變長了 ($n_{ctx}$)，導致推理FLOPs隨之增大。有方法實現推理過程的FLOPs基本恆定不變或變小嗎？（埋個伏筆，注意是基本恆定）。

3. 原理

b: batch

s: sequence length

h: model input dimension

在上面的推理過程中，每 step 內，輸入一個 token序列，經過Embedding層將輸入token序列變爲一個三維張量[b, s, h]，經過一通計算，最後經logits層將計算結果映射至詞表空間，輸出張量維度爲[b, s, vocab_size]。

以上 GPT2 code 爲例： b = 1; s 會每次加 1, 最大到 $n_{ctx}$ ; h = 768; vocab_size = 50257

當前輪輸出token與輸入tokens拼接，並作爲下一輪的輸入tokens，反覆多次。可以看出第 $i+1$ 輪輸入數據只比第 $i$ 輪輸入數據新增了一個token，其他全部相同！因此第 $i+1$輪推理時必然包含了第 $i$ 輪的部分計算。

從 attention block 的角度來看，就是下面的 $x_i : [b, s, h]$ 到下次 $x_{i+1} : [b, s+1, h]$ 每次 token 長度都會加一。計算量也會變大。

step $i$:

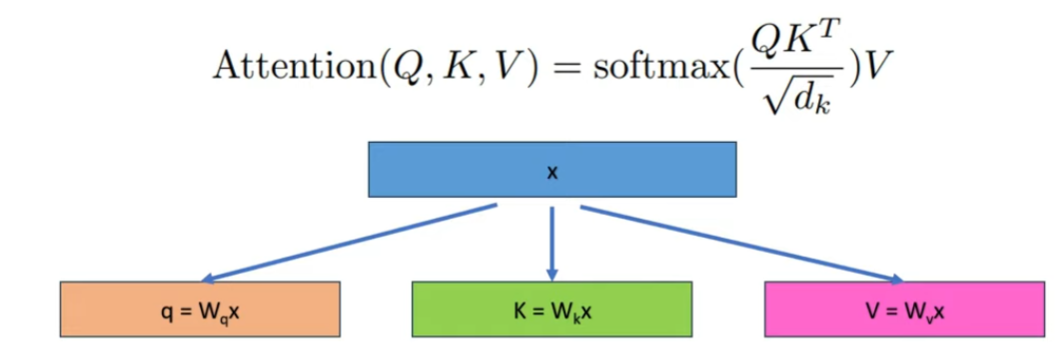
計算 Q, K, V: input 和 output shape at i step: $[b, s, h] \times [h, h] \to [b, s, h]$
計算 $Q K^T$ 矩陣的 input 和 output $ [b, head_{num}, s, d_{head}] \times [b, head_{num}, s, d_{head}] \to [b, head_{num}, s, s]$

step $i+1$:

計算 Q, K, V: input 和 output shape at i+1 step: $[b, s+1, h] \times [h, h] \to [b, s+1, h]$
計算 $Q K^T$ 矩陣的 input 和 output $ [b, head_{num}, s+1, d_{head}] \times [b, head_{num}, s+1, d_{head}] \to [b, head_{num}, s+1, s+1]$

開始是 $s=1, 2, …$, 直到最後 $s = n_{ctx}$ (maximum context length, GPT2 = 1024). 此時已到達 sequence lengthh 的上限 . 接下來每次進來的 token 都會 shift 掉一個最前面的 token. 也就是 $x_{i+1}$ 是 shifted $x_i$.

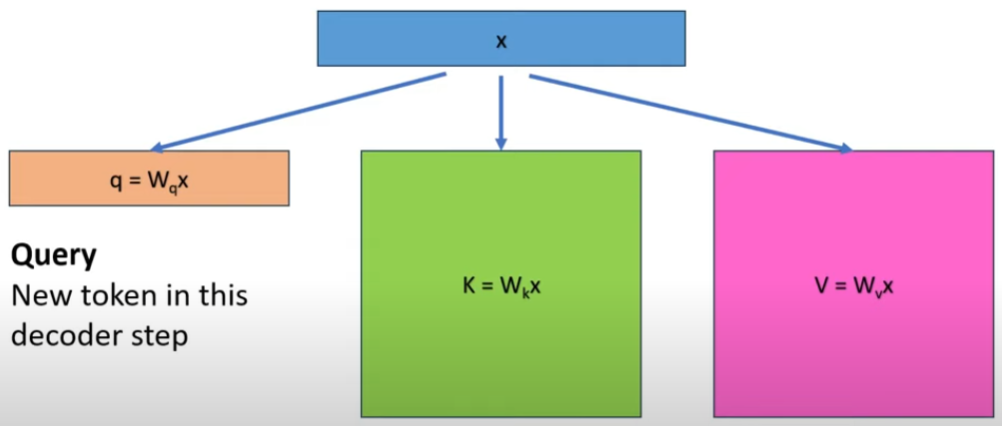
最暴力的方法是每次都計算大的矩陣乘法。但是如果我們可以緩存前一次的 (key, value) 值。是否可以減少重算下一次的 (key, value)?

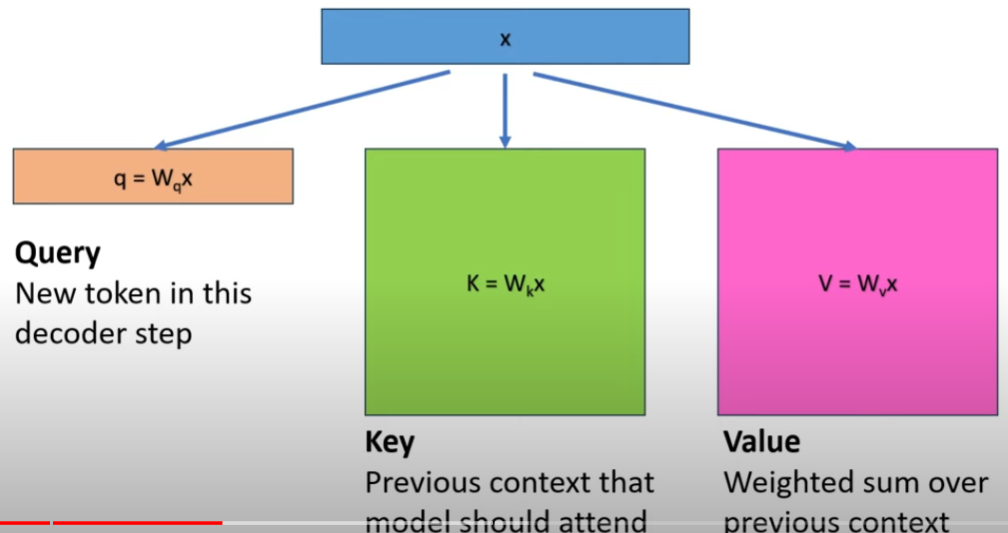
KV Cache的出發點就在這裏，緩存當前輪可重複利用的計算結果，下一輪計算時直接讀取緩存結果，就是這麼簡單，不存在什麼Cache miss問題。

SM stands for SoftMax.

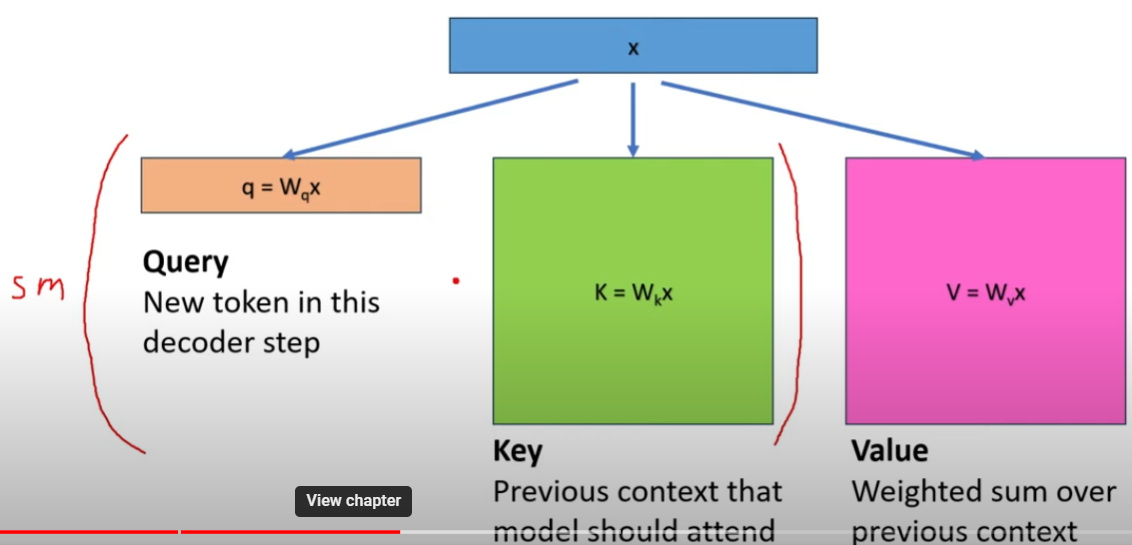
例如在輸入新的 token “chill”，之前的 “cold” 對應的 K vector 和 attention score (V) 其實都不用重算。只需要計算新的 “chill” 對應的 vector 和 attention score (V)

問題：如果是 bi-directional BERT 就需要重算, right?

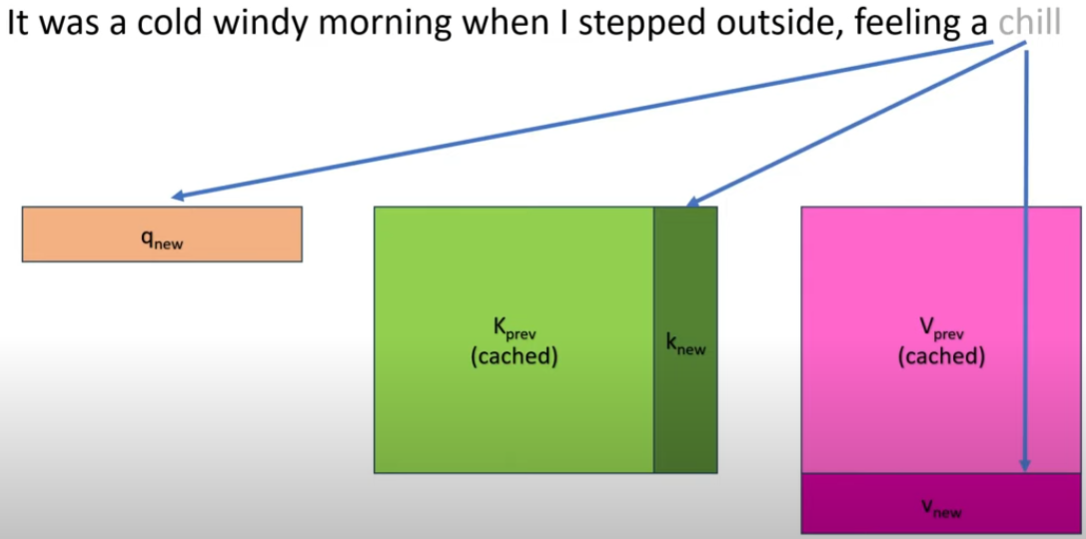
問題：緩存的做法是否可以用在 FFN (feedforward block)? 好像不行? 因爲 FFN input vector shift 之後對應的 weights 就會完全不同？可是 attention 對應的 score 是 position independent? 只有 Attention 有 context and KV cache gain!

KV Cache Memory Usage:

KV parameter count: $2 b s h l$; Memory size: $2 bshl \text{ *precision}$

實現細節

目前各大模型推理都實現了KV Cache，下面就看如何使用了。我們可以在上面代碼基礎上修改，主要改動：

在推理時新增了 past_key_values 參數，該參數就會以追加方式保存每一輪的K V值。kv cache變量內容爲((k,v), (k,v), …, (k,v))，即有 $n_{layers}$ 個 k,v 組成的一個元組，其中 k 和 v 的維度均爲 $[b, n_{head}, s, d_{head}]$。這裏可以順帶計算出每輪推理對應的 cache 數據量爲 2∗b∗s∗ℎ∗$n_{layers}$ ，這裏 s 值等於當前輪次值。以GPT3-175B爲例，假設以 float16 來保存 KV cache，senquence長度爲100，batchsize=1，則 KV cache佔用顯存爲 2×100×12288×96×2 Byte= 472MB。
推理輸出的token直接作爲下一輪的輸入，不再拼接，因爲上文信息已經在 kvcache 中。

代碼示例：

import torch
from transformers import GPT2LMHeadModel, GPT2Tokenizer


model = GPT2LMHeadModel.from_pretrained("/WORK/Test/gpt", torchscript=True).eval()

# tokenizer
tokenizer = GPT2Tokenizer.from_pretrained("/WORK/Test/gpt")
in_text = "Lionel Messi is a"
in_tokens = torch.tensor(tokenizer.encode(in_text))

# inference
token_eos = torch.tensor([198]) # line break symbol
out_token = None
kvcache = None
out_text = in_text
i = 0
with torch.no_grad():
    while out_token != token_eos:
        logits, kvcache = model(in_tokens, past_key_values=kvcache) # 增加了一個 past_key_values 的參數
        out_token = torch.argmax(logits[-1, :], dim=0, keepdim=True)
        in_tokens = out_token # 輸出 token 直接作爲下一輪的輸入，不再拼接
        text = tokenizer.decode(in_tokens)
        print(f'step {i} input: {text}', flush=True)
        i += 1
        out_text += text

print(f' Input: {in_text}')
print(f'Output: {out_text}')

通過上面代碼只能看到調用層面的變化，實現細節還需看各框架的底層實現，例如Hugging Face的transformers庫代碼實現就比較清爽，在modeling_gpt2.py中Attention部分相關代碼如下：

   query = self._split_heads(query, self.num_heads, self.head_dim)
        key = self._split_heads(key, self.num_heads, self.head_dim)
        value = self._split_heads(value, self.num_heads, self.head_dim)

        if layer_past is not None: # 當輸出第一個token後，layer_past就是非None了
            past_key, past_value = layer_past # 取出之前計算好的 key, value
            key = torch.cat((past_key, key), dim=-2) # past_key 與當前 token 對應的 key 拼接
            value = torch.cat((past_value, value), dim=-2) # past_value 與當前 token 對應的 value 拼接

        if use_cache is True:
            present = (key, value)
        else:
            present = None

其實，KV Cache 配置開啓後，推理過程可以分爲2個階段：

預填充階段 ($s = 1,2, .., n_{ctx}$)：發生在計算第一個輸出token過程中，這時Cache是空的，計算時需要爲每個 transformer layer 計算並保存key cache和value cache，在輸出token時Cache完成填充；FLOPs同KV Cache關閉一致，存在大量 GEMM 操作，推理速度慢。 正常推理，預存 key-value cache；compute-bound 計算
使用KV Cache階段：發生在計算第二個輸出token至最後一個token過程中，這時Cache是有值的，每輪推理只需讀取Cache，同時將當前輪計算出的新的Key、Value追加寫入至Cache；FLOPs降低，GEMM 變爲 GEMV 操作，推理速度相對第一階段變快，這時屬於Memory-bound類型計算。memory-bound 計算

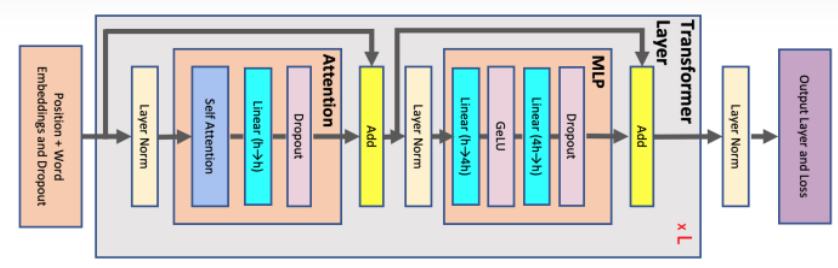
這裏用圖可能更有助理解，下圖是一個Decoder Block，含有Self-Attention和MLP，標紅部分爲KV Cache影響到的內容，即KV Cache開啓後，標紅的序列長度 s 變爲 1，當batch_size=1時，Self-Attention中的2個dense全都變爲gemv操作，MLP中的dense也全都變爲gemv操作。看懂這個圖就可以答對上面的3個問題啦。

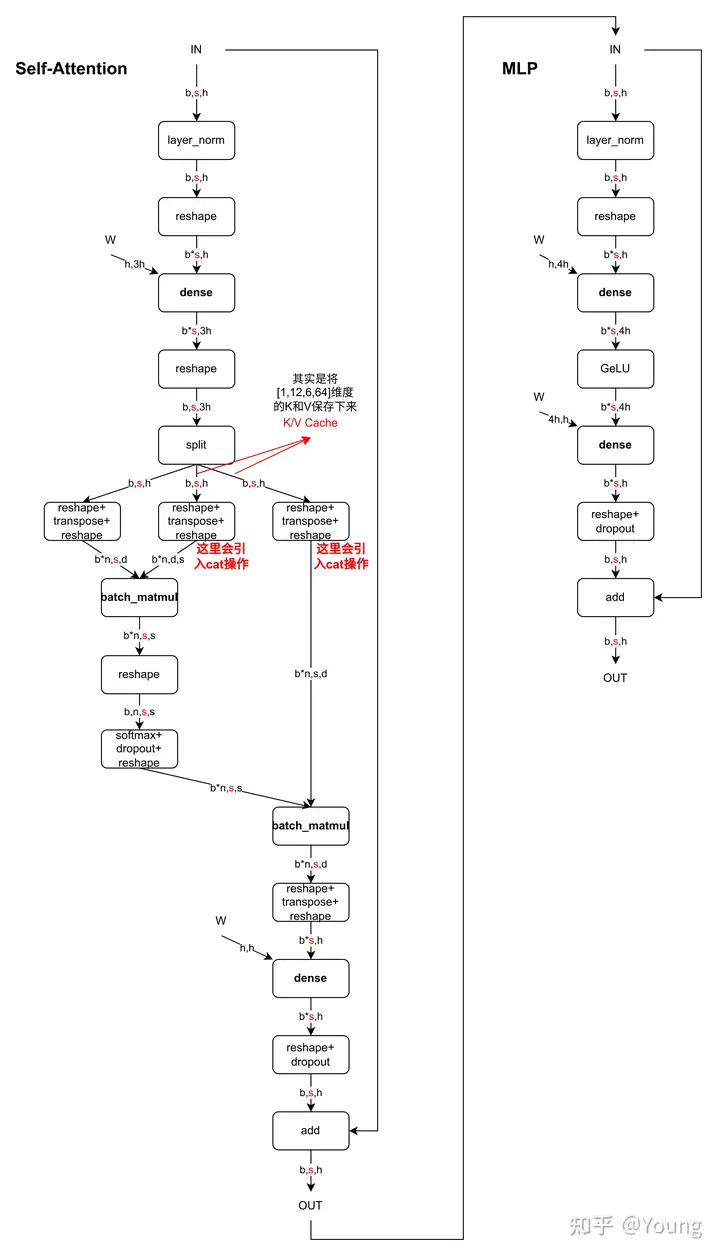
如下鏈接也有這方面的定量分析，寫的很棒，推薦大家看看。

迴旋托馬斯x：分析transformer模型的參數量、計算量、中間激活、KV cache

總結

KV Cache是Transformer推理性能優化的一項重要工程化技術，各大推理框架都已實現並將其進行了封裝（例如 transformers庫 generate 函數已經將其封裝，用戶不需要手動傳入past_key_values）並默認開啓（config.json文件中use_cache=True）。

KV Cache for Inference (主要用於推理)

KV Cache 的主要工作是減少 computation! 不是 DRAM BW reduction! 剛好相反，KV cache 會增加 DRAM bandwidth.

本質上是“空間換時間”。

0-cache 每次都要從 DRAM 讀 parameter 計算所有 output token:
- DRAM BW = parameter size x output token/sec
- Computation = 2 x parameter size TOPS
KV cache 假設 internal SRAM = parameter size + KV cache: 理論上 DRAM access 只需要一次?
- DRAM BW = parameter size x output token/sec + KV cache size x 6 x output token/sec?
- DRAM BW / token = parameter size + KV cache size x 6 (讀幾次? 寫幾次?)
- Computation = ?? TOPS (減少 s 倍) 見下文

是否可能 “時間換空間”? On-die 7GB 或是 3.5GB SRAM，不可能！

在推斷階段，transformer模型加速推斷的一個常用策略就是使用 KV cache。一個典型的大模型生成式推斷包含了兩個階段：

預填充階段：輸入一個prompt序列，爲每個transformer層生成 key cache和value cache（KV cache）。
解碼階段：使用並更新KV cache，一個接一個地生成詞，當前生成的詞依賴於之前已經生成的詞。

第 $i$個transformer層的權重矩陣爲 $W_Q^i, W_K^i, W_V^i, W_O^i, W_1^i, W_2^i$。

其中 self-attention 的 4 個權重矩陣 $W_Q^i, W_K^i, W_V^i, W_O^i \in R^{h \times h}$。

並且MLP塊的2個權重矩陣 $W_1^i \in R^{h \times 4h}, W_2^i \in R^{4h \times h}$。

預填充階段

假設第 $i$個transformer層的輸入爲 $x^i$ ，self-attention塊的key、value、query和output表示爲 $x_K^i, x_V^i, x_Q^i, x_{out}^i$ 其中 $x_K^i, x_V^i, x_Q^i, x_{out}^i \in R^{b\times s\times h}$。

Key cache 和 value cache 的計算過程為

$x_K^i = x^i \cdot W_K^i$

$x_V^i = x^i \cdot W_V^i$

第 $i$ 個 transformer 層剩餘的計算過程為

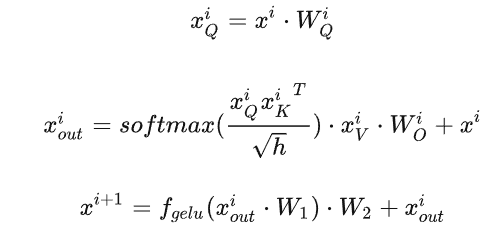
解碼階段

給定當前生成詞在第 $i$ 個transformer層的向量表示爲 $t^i \in R^{b \times 1 \times h}$. 推理計算分兩部分：更新 KV cache 和計算第 $i$ 個 transformer 層的輸出。

更新 key cache 和 value cache 的計算過程如下：

計算量減少分析：

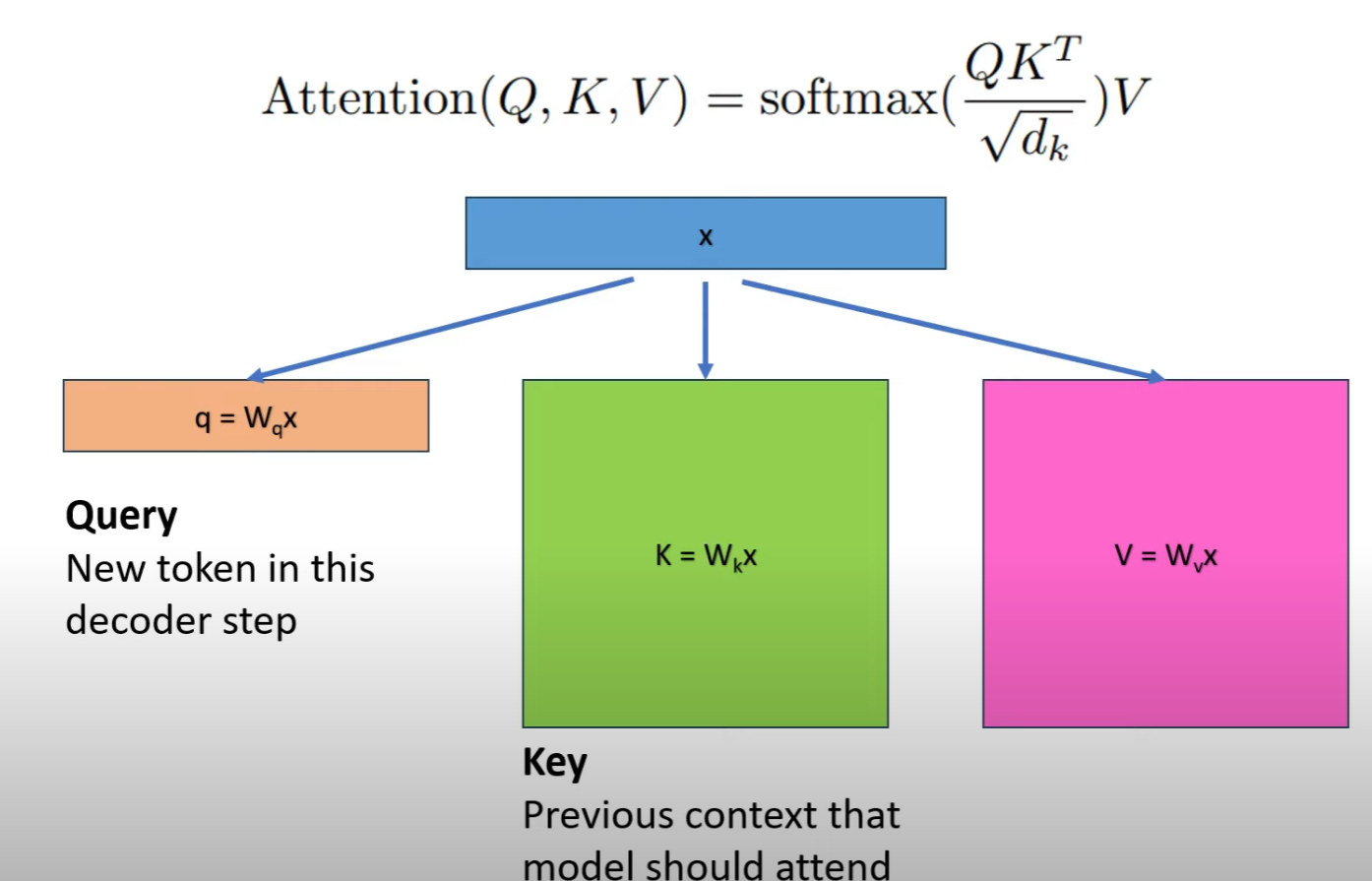
輸入數據的形狀爲 [b,1,ℎ]，kv cache中含有kv_length個past word。我們先分析self-attention塊的計算，

計算 Q, K, V ：矩陣乘法的輸入和輸出形狀爲 [b,1,ℎ]×[ℎ,ℎ]→[b,1,ℎ] 。計算量爲 3∗2bℎ2=6bℎ2 。
QK^T 矩陣乘法的輸入和輸出形狀爲[b, head_num, 1, per_head_hidden_size]×[b, head_num, per_head_hidden_size, kv_length+s]→[b,head_num,1,kv_length+1] 。計算量爲 2bs (kv_length +1 )ℎ 。
計算在V上的加權 score . V ，矩陣乘法的輸入和輸出形狀爲 [b, head_num, 1, kv_length+1]×[b,head_num,kv_length+1,per_head_hidden_size]→[b,head_num,1,per_head_hidden_size] 。計算量爲 2bs(kv_length +1)ℎ 。
attention後的線性映射，矩陣乘法的輸入和輸出形狀爲 [b,1,ℎ]×[ℎ,ℎ]→[b,1,ℎ] 。計算量爲 2bℎ^2 。

接下來分析MLP塊的計算，計算公式如下：

第一個線性層，矩陣乘法的輸入和輸出形狀爲 [b,1,ℎ]×[ℎ,4ℎ]→[b,1,4ℎ] 。計算量爲 8bℎ2 。
第二個線性層，矩陣乘法的輸入和輸出形狀爲 [b,1,4ℎ]×[4ℎ,ℎ]→[b,1,ℎ] 。計算量爲 8bℎ2 。

將上述計算量相加，得到每個transformer層的計算量大約爲 24 b h2 + 4bℎ+4b(kv_length )ℎ 。

不採用kv cache時爲： 24 b sh ℎ2+4 b s2 ℎ

此外，另一個計算量的大頭是logits的計算，將隱藏向量映射爲詞表大小。矩陣乘法的輸入和輸出形狀爲 [b,1,ℎ]×[ℎ,V]→[b,1,V] ，計算量爲 2bℎV 。

不採用kv cache時爲： 2bsℎV

Attention 的計算量可以節省 s 倍！ Really??

KV cache 額外的顯存佔用分析

存儲 kvlength 個K｜V value，形狀爲 [b, head_num, kv_seq_len, head_dim]，
顯存佔用爲： 4blh(kv_length)

假設輸入序列的長度爲 $s$，輸出序列的長度爲 $n$，以float16來保存KV cache，那麼KV cache的峯值顯存佔用大小爲 $b(s+n)hl2*2 = 4blh(s+n)$。這裏第一個2表示K/V cache，第二個2表示float16佔2個bytes。

Training 的中間激活時 : $34 blsh + 11 b l s^2 a$, KV cache 只存了 attention 中的 K and V 部分，有包含 score?
Model 參數量是 $12 l h^2$ (和 b, s 無關！), 假設是 16-bit, Model 內存是 $24 l h^2$
假設 inference $b=1$ (這不一定是對的，在 speculative decode, 大 model 的 $b > 1$): KV cache : $4 blh (s+n)$. KV cache / model parameter ~ $b (s+n) / 6 h$! 對於 long context, $s + n$ 可能會大於 $h$!! $s$ 就是 $n_{ctx}$, $h$ 就是 $d_{model}$
以 Llama2-7B 爲例, $h = 4096$, 但是 $n_{ctx} 最大也有 4096$!

#####

Example Llama2 (4A16W)

以 Llama2-7B 爲例。

模型名	參數量	層數, l	隱藏維度, h	注意力頭數 a	Context s
Llama2-7B	7B	32	4096	32	4096
Llama2-13B	13B	40	5120	40	4096
Llama2-33B	33B	60	6656	52	4096
Llama2-70B	70B	80	8192	64	4096

Llama2 的模型參數量爲7B，佔用的顯存大小爲 (INT8) 7Bx2 = 7GB 。假設 activation 是 FP16.

假設 Llama2 的序列長度 $s$ 爲 2048 。對比不同的批次大小 $b$ 佔用的中間激活：

當 b=1 時，KV cache 佔用顯存爲 $(4bsh)*l$ byte ≈1GB ，大約是模型參數顯存的15%。

假設 Llama2 的序列長度 $s$ 爲 4096 。對比不同的批次大小 $b$ 佔用的中間激活：

當 b=1 時，KV cache 佔用顯存爲 $(4bsh)*l$ byte ≈2.1GB ，大約是模型參數顯存的31%。

如果 model 是 4-bit (4W16A) 7Bx0.5 = 3.5GB, 更糟糕: KV cache 佔的比例 double.

Example GPT3-175B (8A16W)

以GPT3-175B爲例，我們來直觀地對比下模型參數與中間激活的顯存大小。GPT3的模型配置如下。我們假設採用混合精度訓練，模型參數和中間激活都採用float16數據類型，每個元素佔2個bytes。

模型名	參數量	層數, l	隱藏維度, h	注意力頭數 a
GPT3	175B	96	12288	96

GPT3的模型參數量爲175B，佔用的顯存大小爲 1×175B = 175GB for inference。

GPT3的序列長度 $s$ 爲 2048 。對比不同的批次大小 $b$ 佔用的中間激活：

b=1 ，輸入序列長度 s=2048, 中間激活佔用顯存爲 $(4bsh)*l$ byte ≈9.7GB ，大約是模型參數顯存的 5.6%。

b=64 ，輸入序列長度 s=512 ，輸出序列長度 n=32 ，則KV cache佔用顯存爲 $4blh(s+n) = 164 GB$，大約是模型參數顯存的 1 倍。

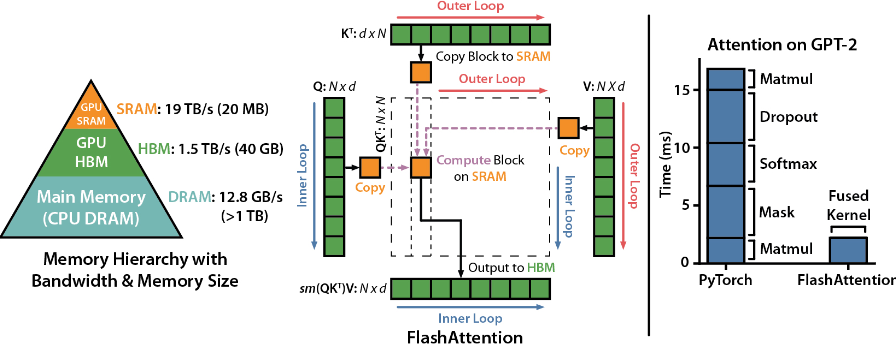
GPU Memory Hierarchy

先比較一下常見的 edge device memory hierarchy.

	Compute Core	SRAM Size/BW	1st Mem Size/BW	2nd Mem Size/BW
A100	(FP16) 312 TOPS Tensor	20MB / 19TB/s	(HBM2?) 40GB / 1.5TB/s	CPU DRAM > 1TB / 12.8GB/s
Smartphone	(INT8) 40 TOPS	8MB / ??	(LP5-8500, 64bit) 12GB / 50GB/s	Flash, 512TB / 1GB/s?
RTX4070TI	7680 Shader 184 Tensor (FP32) 40 TOPS		(G6X, 192bit) 12GB / 504GB/s	NA