LLM 計算量分析

Posted on | In

Source

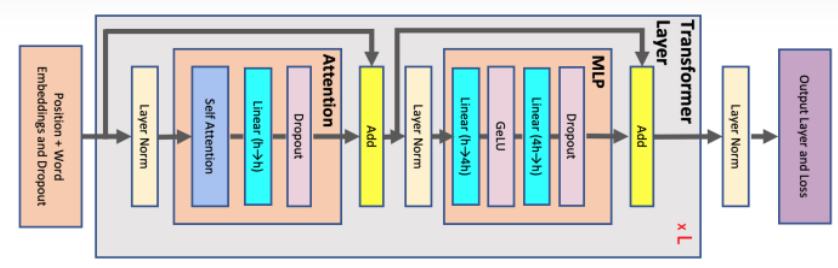
image-20231029165342034

Takeaway

  • Short context ( $s \ll h$): 假設当隐藏维度 h 比较大，且远大于序列长度 s 时，計算量 / token : ~ 2 x 參數量! 可以近似認爲: 在一次前向传递中，对于每个token，每个模型参数，需要进行2次浮点数运算，即一次乘法法运算和一次加法运算。
  • Llama2 1/2/4K context 的計算量/token 大約是參數量 x 2. 但是在 32K long context 的 attention 計算 ($4bs^2 h$) 量大幅增加，比例超出參數量的 2 倍。
  • Attention 計算量的比例大約是 1/3 (33%), MLP 計算量比例大約是 2/3 (66%).

計算量

Training/Inference

Self attention

b = batch 在 training 時，會有 batch input, 在 inference 是 batch = 1 for ChatGPT model.

s = n_ctx (input tokens)

h = d_model ( = num_head * d_head)

  • 此處考慮 batch size, 因爲 training.
  • ChatGPT inference 的 batch size = 1. 以及在某些 network (大小網絡) batch size > 1 可以加速。

K, Q, V: Mapping Matrix : $Q = x_{in} W_Q，K = x_{in} W_K， V = x_{in} W_V$

  • 計算 Q, K, V: input 和 output shape [b, s, h] x [h, h] –> [b, s, h]
  • 計算量 $3 * 2 b s h^2 = 6 b s h^2$

QK: Attention matrix $x_{out} = \text{softmax}\left( \frac{Q K^T}{\sqrt{h}}\right) \cdot V \cdot W_O + x_{in}$

  • 此處要考慮 multi-heads, 因此把 3D 的 Q, K, V [b, s, h] reshape 成 4D [b, head_num, s, per_head_hidden_size] where h = d_model = head_num * per_head_hidden_size
  • $Q K^T$ 矩陣的 input 和 output [b, head_num, s, per_head_hidden_size] x [b, head_num, per_head_hidden_size, s] –> [b, head_num, s, s]
  • 計算量: $2 b s^2 h$! 注意如果是 long context, s 可能會非常大, 1/2K -> 4/8/16/32K

Softmax $x_{out} = \text{softmax}\left( \frac{Q K^T}{\sqrt{h}}\right) \cdot V \cdot W_O + x_{in}$

  • input 和 output shape 都是: [b, head_num, s, s]
  • Softmax 計算量: $2 s^2 \text{head}_{num}$! 注意如果是 long context, s 可能會非常大, 1/2K -> 4/8/16/32K

Score $x_{out} = \text{softmax}\left( \frac{Q K^T}{\sqrt{h}}\right) \cdot V \cdot W_O + x_{in}$

  • input 和 output shape 都是: [b, head_num, s, s] x [b, head_num, s, per_head_hidden_size] –> [b, head_num, s, per_head_hidden_size]
  • 計算量: $2 b s^2 h$! 注意如果是 long context, s 可能會非常大, 1/2K -> 4/8/16/32K

Output Mapping $x_{out} = \text{softmax}\left( \frac{Q K^T}{\sqrt{h}}\right) \cdot V \cdot W_O + x_{in}$

  • input 和 output shape 都是: [b, s, h] x [h, h] –> [b, s, h]
  • 計算量: $2 b s h^2$
Self-Attention 的計算量

MAC: $6 b s h^2 + 2 b s^2 h + 2 b s^2 h + 2 b s h^2 = 8 b s h^2 + 4 b s^2 h$

Softmax: $2 s^2 \text{head}_{num}$

MLP
\[x_{mlp} = f_{gelu} (x_{out} W_1) W_2 + x_{out}\]
  • 第一個 FC (W1)，矩陣乘法的輸入和輸出 [b, s, h] x [h, 4h] –> [b, s, 4h]
  • 計算量是 $8 b s h^2$
  • 第二個 FC (W2)，矩陣乘法的輸入和輸出 [b, s, 4h] x [4h, h] –> [b, s, h]
  • 計算量是 $8 b s h^2$
MLP 的計算量

MAC: $16 b s h^2 $

Layer Normalization - 參數 $\gamma, \beta$ : $4 d_{model} = 4h$

  • Self-attention 和 FFN 各有一個 layer normalization. 包含兩個可訓練的參數：縮放參數 $\gamma$ 和平移參數 $\beta$, 形狀都是 $d_{model}$. 因此兩個 layer normalization 的參數量是 $4 d_{model}$
  • Input, output [b, s, h] –> [b, h]
  • 計算量是 $4 bsh$

Self-attention + MLP 計算量

每個 transformer 層的計算量： $24 b s h^2 + 4 b s^2 h$

所以所有的計算量 = $l * (24 b s h^2 + 4 b s^2 h)$

還有一個計算量的大頭是 input 和 output token to 字

  • Input, output [b, s, h] x [h, V] –> [b, s, V]
  • 計算量 2 b s h V.
  • Total : $2 b s h V + l * (24 b s h^2 + 4 b s^2 h)$

參數量和計算量的關係

Short context ( $s \ll h$): 假設当隐藏维度 h 比较大，且远大于序列长度 s 时， 我们可以忽略一次项，计算量可以近似为

計算量 ~ $24 l b s h^2$, 此時對應的參數量是 $12 l h^2$ (和 s 無關！)，一次得到 $b s$ tokens.

  • 總計算量 : ~ 2 x 參數量 x 輸入 tokens! 可以近似認爲: 在一次前向传递中，对于每个token，每个模型参数，需要进行2次浮点数运算，即一次乘法法运算和一次加法运算。

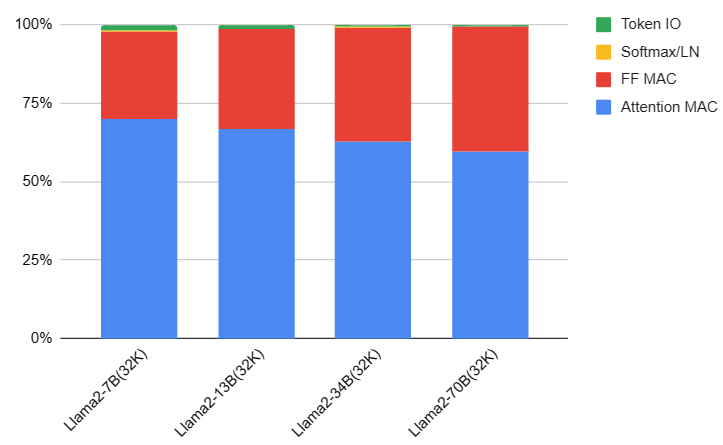
  • 下圖可以看出 Llama2 1/2/4K context 的計算量/token 大約是參數量 x 2. 但是在 32K long context 的 attention 計算 ($4bs^2 h$) 量大幅增加。

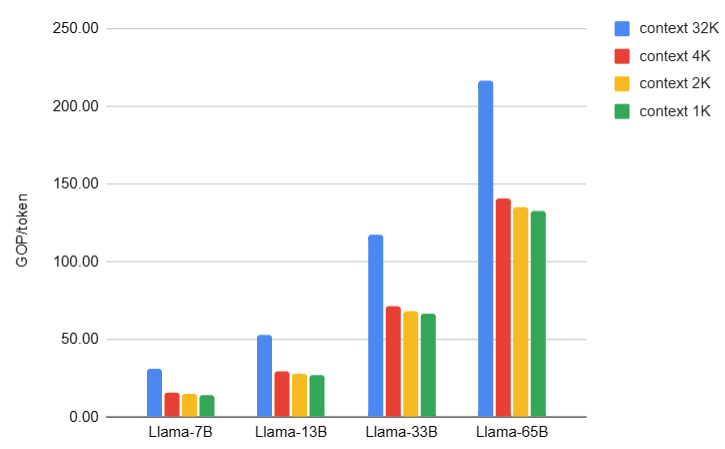
  • image-20231104113213414

  • 另外在 attention 計算量的比例大約是 1/3 (33%), MLP 計算量比例大約是 2/3 (66%).

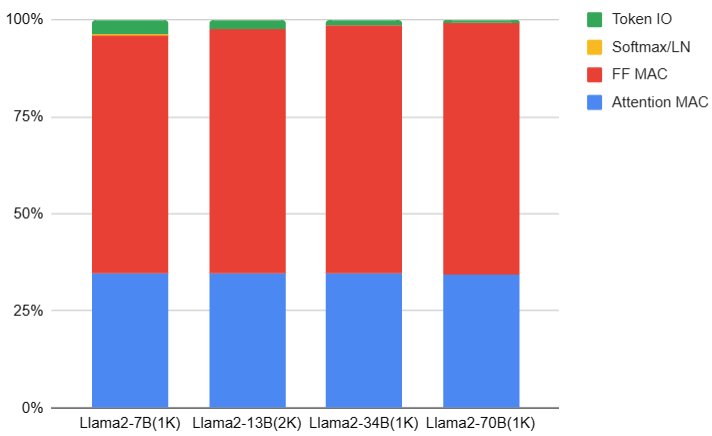
    • 下圖是 Llama2 with short context (1K) 的計算量比例： image-20231104111651874

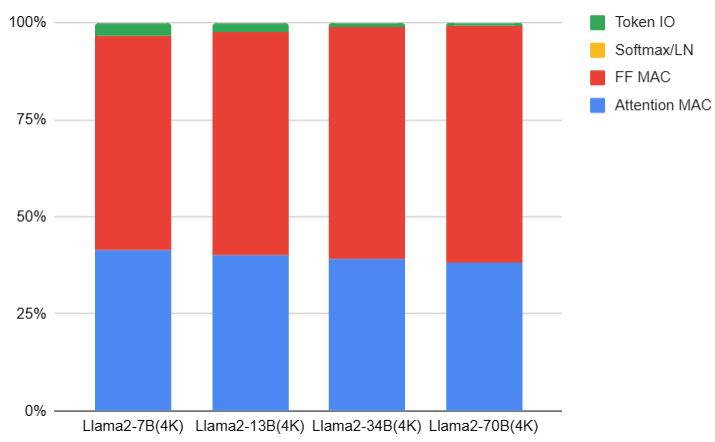
    • 下圖是 Llama2 with default context (4K) 的計算量比例：(attention 計算量比例增加 from 34% to 40%) image-20231104111804759

    • 下圖是 Llama2 with super long context (32K) 的計算量比例：(attention 計算量比例增加到 60-70%) image-20231104111946462

  • 一次训练迭代包含了前向传递和后向传递，后向传递的计算量是前向传递的2倍。因此，前向传递 + 后向传递的系数 =1+2=3 。一次训练迭代中，对于每个token，每个模型参数，需要进行 2∗3=6 次浮点数运算。

Example: LLama-7B Inference

如果是 inference: bs = 1 per token.

如果是 training: bs 非常大

A: input token and first output token: 1024 output at 1 sec = 2 x 參數量 (7B=7G parameter) x 1024 = 14 TOPs

B: sustained output tokens: 2 x 參數量 (7B model = 7G parameter) x output token rate = 14 GOP/token x 10 token/sec = 140 GOP/sec

Example: GPT3-175B Training

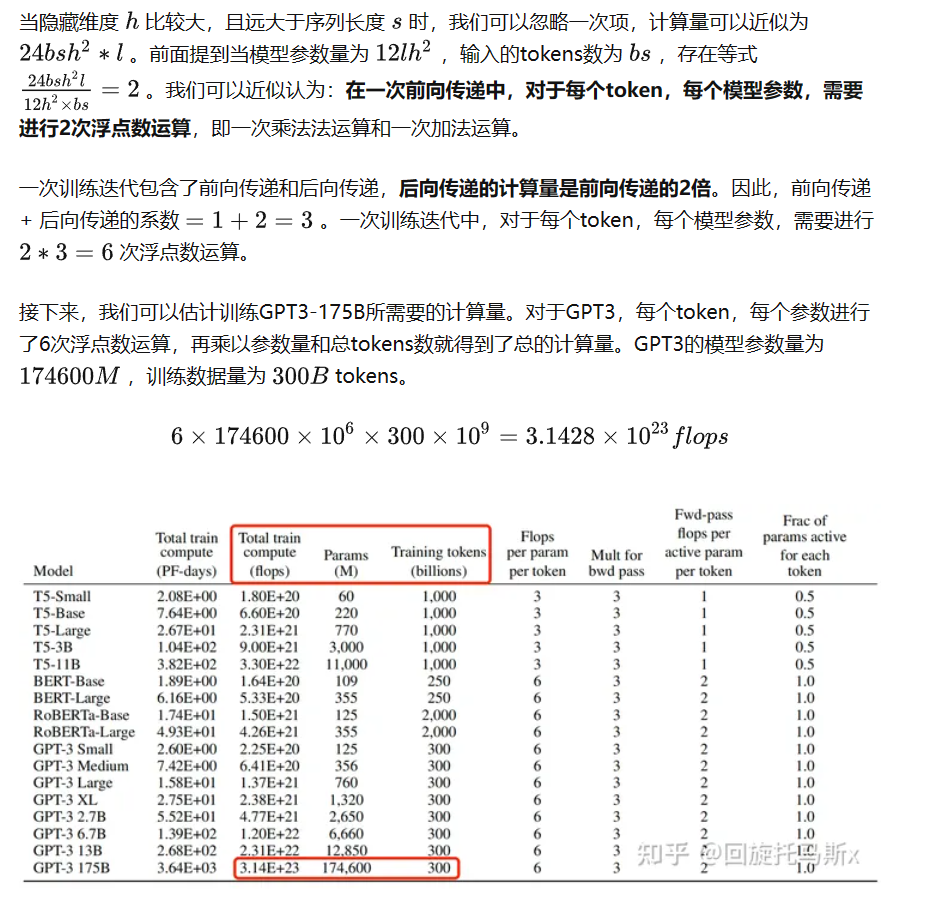
每个token，每个参数进行了6次浮点数运算，再乘以参数量和总tokens数就得到了总的计算量。GPT3的模型参数量为 175B ，训练数据量为 300B tokens。

Training 計算量: 6 x 175B x 300B = 3.15 x 10^23 Flop

image-20231022090609054

3.2 训练时间估计 (Training)

模型参数量和训练总tokens数决定了训练transformer模型需要的计算量。给定硬件GPU类型的情况下，可以估计所需要的训练时间。给定计算量，训练时间（也就是GPU算完这么多flops的计算时间）不仅跟GPU类型有关，还与GPU利用率有关。计算端到端训练的GPU利用率时，不仅要考虑前向传递和后向传递的计算时间，还要考虑CPU加载数据、优化器更新、多卡通信和记录日志的时间。一般来讲，GPU利用率一般在 0.3∼0.55 之间**。

上文讲到一次前向传递中，对于每个token，每个模型参数，进行2次浮点数计算。使用激活重计算技术来减少中间激活显存（下文会详细介绍）需要进行一次额外的前向传递，因此前向传递 + 后向传递 + 激活重计算的系数=1+2+1=4。使用激活重计算的一次训练迭代中，对于每个token，每个模型参数，需要进行 2∗4=8 次浮点数运算。在给定训练tokens数、硬件环境配置的情况下，训练transformer模型的计算时间为：