Attention As Graph

Posted on | In

Source

Takeaway

Karpathy 有幾個 key concept 非常好!

  • Attention 是 token to token communication, FFC/MLP 是每個 token 内部的 computation.
  • LLM 的參數，原理上就是 (lossy) compression (所以服從 Shannon Information Theory?)

image-20231029165342034

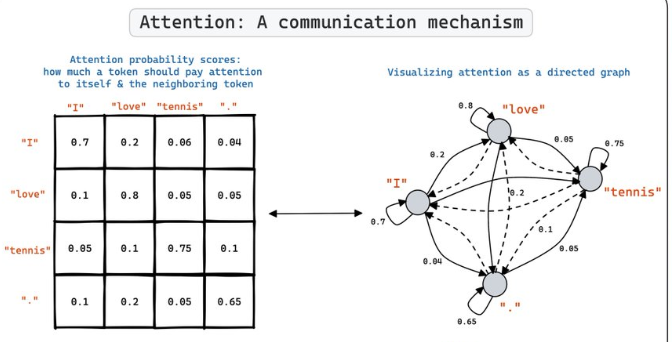
Attention Matrix as a Graph

下圖是 “I love tennis.” 的 attention matrix. 可以詮釋成 Directed Graph 如下圖。但是並非常見的 Directed Acyclic Graph (DAG).

這有什麽用嗎?

  • Markov matrix, 類似 transition probability matrix. 代表每個 token 和 自己以及其他 tokens 的 transition probability?
  • 只有 forward direction 有用? 有實務上的用途嗎? 是否可以用來計算 perplexity?

image-20231125134912754

Perplexity of a fixed-length large language model

image-20231125143025058

以上式來看，log 的 summation and average 對應是機率倒數的幾何平均值！不是 entropy 的單位。

  • PPL 内部的條件機率: \(p(x_1) p(x_2\|x_1) p(x_3\|x_2,x_1) p(x_4\|x_3,x_2,x_1)\cdots p(x_t \| x_{t-1},\cdots x_1) = p(x_1) \frac{p(x_1,x_2)}{p(x_1)} \frac{p(x_3,x_2,x_1)}{p(x_1,x_2)} \cdots = p(x_1, x_2, ... x_t)\)

  • 接下來 exp 和 log 互相抵銷，PPL 是條件機率的幾何平均值的倒數 = $\sqrt[t]{p(x_1,\cdots,x_t)^{-1}}$. 因此 PPL 的最小值是 1. 對應所有條件機率 = 1. 當然實務上機率必然小於 1, 所以倒數大於 1. 除非 joint distribution 是 delta function，不然 PPL 一定大於 1. 如果 joint distribution 的 entropy 越大, PPL 就越大。
  • 這個 attention or transition probability 好像只有 forward pass 有用，不能 backward ?

Attention 的來源

  1. 先把 input words 轉換成 tokens. 這是一個 trade-off between vocab_size 和 token length.
    • 如果使用很小的 vocab_size, 例如 English characters (vocab_size < 100), 會造成很長的 token lengths. 這會產生非常大的 attention matrix, 造成大量的 communication and computation burden.
    • 反之使用很大的 vocab_size, 例如所有的 English words (vocab_size > 10000), 雖然 token length 很短，但是缺少 communication between tokens, 會造成準確性下降?
  2. 再把 token maps to embedding，也就是 vectors.
  3. 再來就是有名的 K, Q (, and V) vectors. 其中 K, Q 用來計算 K, Q matrix, 也就是 attention matrix. 也就是不同 token 之間的 transition probability.
  4. 接下來是產生 output embedding (token), 就是把 attention matrix 乘以 V vector.

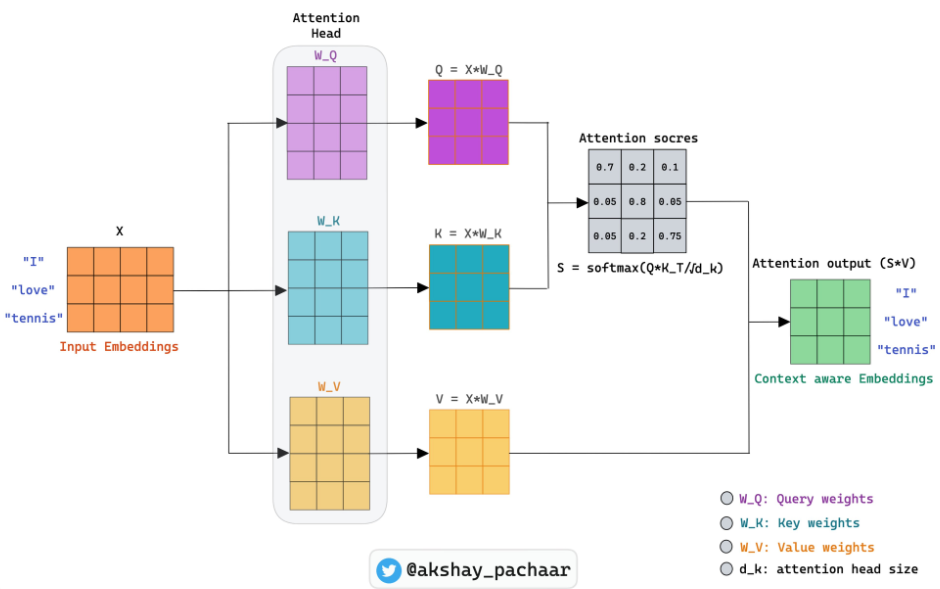
image-20231127211021581

Self attention is a communication mechanism

Query: 我要找這個 information

Key: 我有這個 information

Value:

Language model

Self-attention: Q and K are the same (所以 matrix 是 symmetric? no); V is also the same.

Cross-attention: Q, K from encoder, V from decoder?

Recommendation System

Q is target? K, V 對應 user profile and product profile?

image-20231128221957731

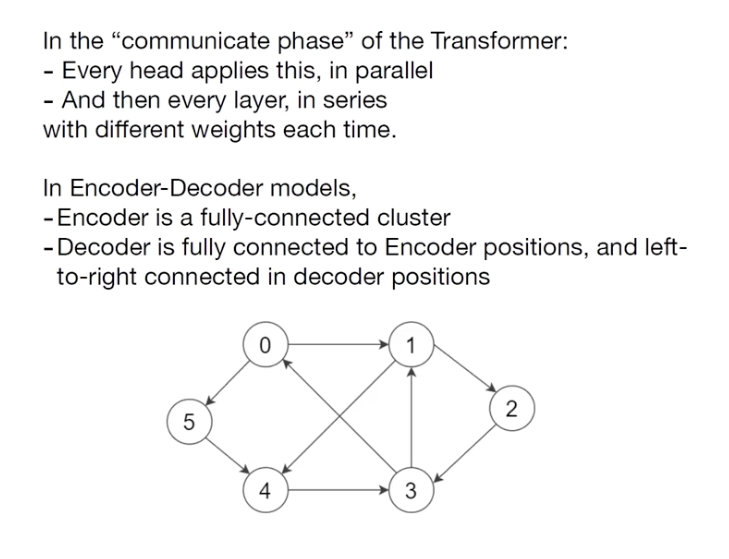
image-20231128222022189

二階段: communication and computation

image-20231128222747774

Appendix

Hugging Face Perplexity Example

使用 GPT-2 ($n_{ctx} = 1024$) 計算 perplexity.

這裏使用 Hugging face 的 GPT2 和 WikiText dataset. 要事先 install 以下 packages.

1
2
pip install transformer
pip install datasets

1
2
3
4
5
6
from transformers import GPT2LMHeadModel, GPT2TokenizerFast

device = "cuda"
model_id = "gpt2-large"
model = GPT2LMHeadModel.from_pretrained(model_id).to(device)
tokenizer = GPT2TokenizerFast.from_pretrained(model_id)

我們用 WikiText-2 dataset 評估 PPL.

1
2
3
4
from datasets import load_dataset

test = load_dataset("wikitext", "wikitext-2-raw-v1", split="test")
encodings = tokenizer("\n\n".join(test["text"]), return_tensors="pt")

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import torch
from tqdm import tqdm

max_length = model.config.n_positions
stride = 512
seq_len = encodings.input_ids.size(1)

nlls = []
prev_end_loc = 0
for begin_loc in tqdm(range(0, seq_len, stride)):
    end_loc = min(begin_loc + max_length, seq_len)
    trg_len = end_loc - prev_end_loc  # may be different from stride on last loop
    input_ids = encodings.input_ids[:, begin_loc:end_loc].to(device)
    target_ids = input_ids.clone()
    target_ids[:, :-trg_len] = -100

    with torch.no_grad():
        outputs = model(input_ids, labels=target_ids)

        # loss is calculated using CrossEntropyLoss which averages over valid labels
        # N.B. the model only calculates loss over trg_len - 1 labels, because it internally shifts the labels
        # to the left by 1.
        neg_log_likelihood = outputs.loss

    nlls.append(neg_log_likelihood)

    prev_end_loc = end_loc
    if end_loc == seq_len:
        break

ppl = torch.exp(torch.stack(nlls).mean())

最後 ppl = 16.45.