Source
- Break the Sequential Dependency of LLM Inference Using Lookahead Decoding
- https://lmsys.org/blog/2023-11-21-lookahead-decoding/
- https://github.com/hao-ai-lab/LookaheadDecoding
- Llama C version:
Takeaway
- Transformer model 最大的好處!!
- Distribution probability 直接就在 softmax 之後!!
- 要加速,就是要打破 sequence dependency, 並利用 parallel verification
- 有幾種方法
- Draft model (小模型) + 原始模型
- 原始模型 + 多頭 Medusa
- 原始模型 + Lookahead
加速比較
| Speculative Decode | Medusa | Lookahead Decode | |
|---|---|---|---|
| Model | Small Draft + Large Native models | Large + Multihead | Large + Lookahread |
| Overhead | 10% | 7% | ?% |
| Speed up | Depends on small model 大 model 最好 |
2x | 小 model 最好? |
| Input | Sequential from draft model | Jacobe? | |
| Output | Parallel verify | Parallel verify |
Lookahead Key Technology
$\boldsymbol{x}$ : prompt, $\boldsymbol{y}=\left[y_1, y_2, \ldots, y_m\right]: m$ tokens to decode, $p(\boldsymbol{y} \mid \boldsymbol{x}):$ LLM distribution
Define: $f\left(y_i, \boldsymbol{y}{1: i-1}, \boldsymbol{x}\right)=y_i-\operatorname{arg max} p\left(y_i \mid \boldsymbol{y}{1: i-1}, \boldsymbol{x}\right)$ \(\left\{\begin{array} { l } { y _ { 1 } = \operatorname { arg max } p ( y _ { 1 } | \boldsymbol { x } ) } \\ { y _ { 2 } = \operatorname { arg max } p ( y _ { 2 } | y _ { 1 } , \boldsymbol { x } ) } \\ { \vdots } \\ { y _ { m } = \operatorname { arg max } p ( y _ { m } | \boldsymbol { y } _ { 1 : m - 1 } , \boldsymbol { x } ) } \end{array} \quad \equiv \quad \left\{\begin{array}{l} f\left(y_1, \boldsymbol{x}\right)=0 \\ f\left(y_2, y_1, \boldsymbol{x}\right)=0 \\ \vdots \\ f\left(y_m, \boldsymbol{y}_{1: m-1}, \boldsymbol{x}\right)=0 \end{array}\right.\right. \\ \text{Autoregressive decoding}\quad \text{Nonlinear system with m variables and m equations}\) $m$ 代表 $m$-gram? No, $m$ 是 token number.
An alternative approach based on Jacobi iteration can solve all $[y_1,y_2,…,y_m]$ of this nonlinear system in parallel as follows:
- Start with an initial guess for all variables $y = [y_1,y_2,…,y_m]$.
- Calculate new y′ values for each equation with the previous y.
- Update y to the newly calculated y′.
- Repeat this process until a certain stopping condition is achieved (e.g., y=y′).
We illustrate this parallel decoding process (also referred to as Jacobi decoding) in Figure 3. Jacobi decoding can guarantee solving all $m$ variables in at most $m$ steps (i.e., the same number of steps as autoregressive decoding) because each step guarantees at least the very first token is correctly decoded. Sometimes, multiple tokens might converge in a single iteration, potentially reducing the overall number of decoding steps.
Jacob Decode
Jacob decode 原理如下:
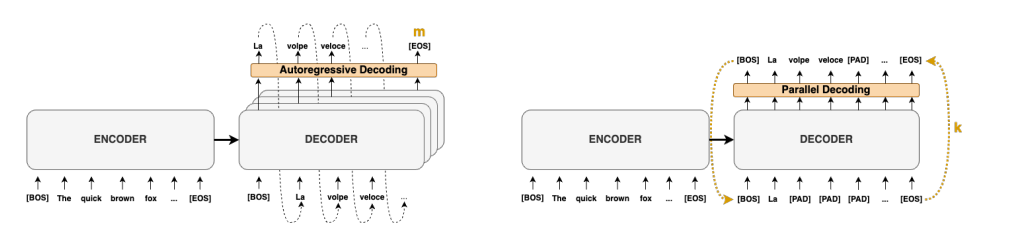
- 左圖是傳統的 autoregressive decode. 需要 $m$ 個 step 才能得到 $m$ tokens.
- 右圖是 Jocob parallel decode. 可以想像 parallel decoding 的 input 是 guess tokens, 經過 parallel decoding 產生 output tokens. Output tokens 經過 decoder 做 parallel verification. 經過 $k$ 次 iteration 得到 $m$ tokens. 如果算法夠聰明,讓 $k < m$, 基本就賺到。Speed up = $m/k$.
- Jacob decode 就是這個”聰明的算法“。
- Autoregressive decoding 的算法就是下表左。

- Jocob 算法就是利用上表右,得到的下表:
- Stop criterion: 就是 input m tokens 等於 output m tokens => fully verified. 如果 k 次達成而且 $k < m$ 就有 speed up.

如何得到 guess tokens? Jacob decode. 問題:如何得到 $p_{\theta}()$ conditional probability.
Transformer model 最大的好處!!
- Distribution probability 直接就在 softmax 之後!!
Parallel verified: 和 speculative decode 一樣
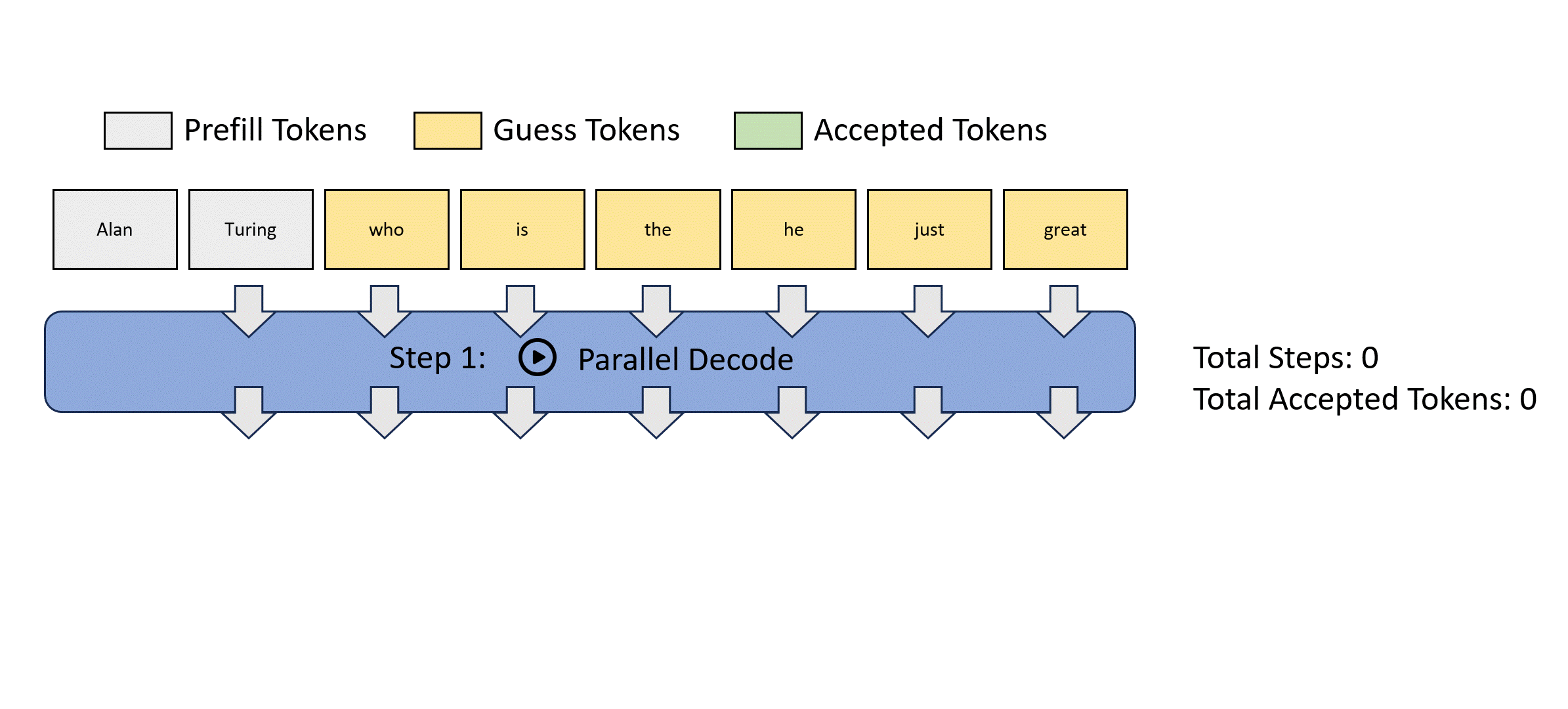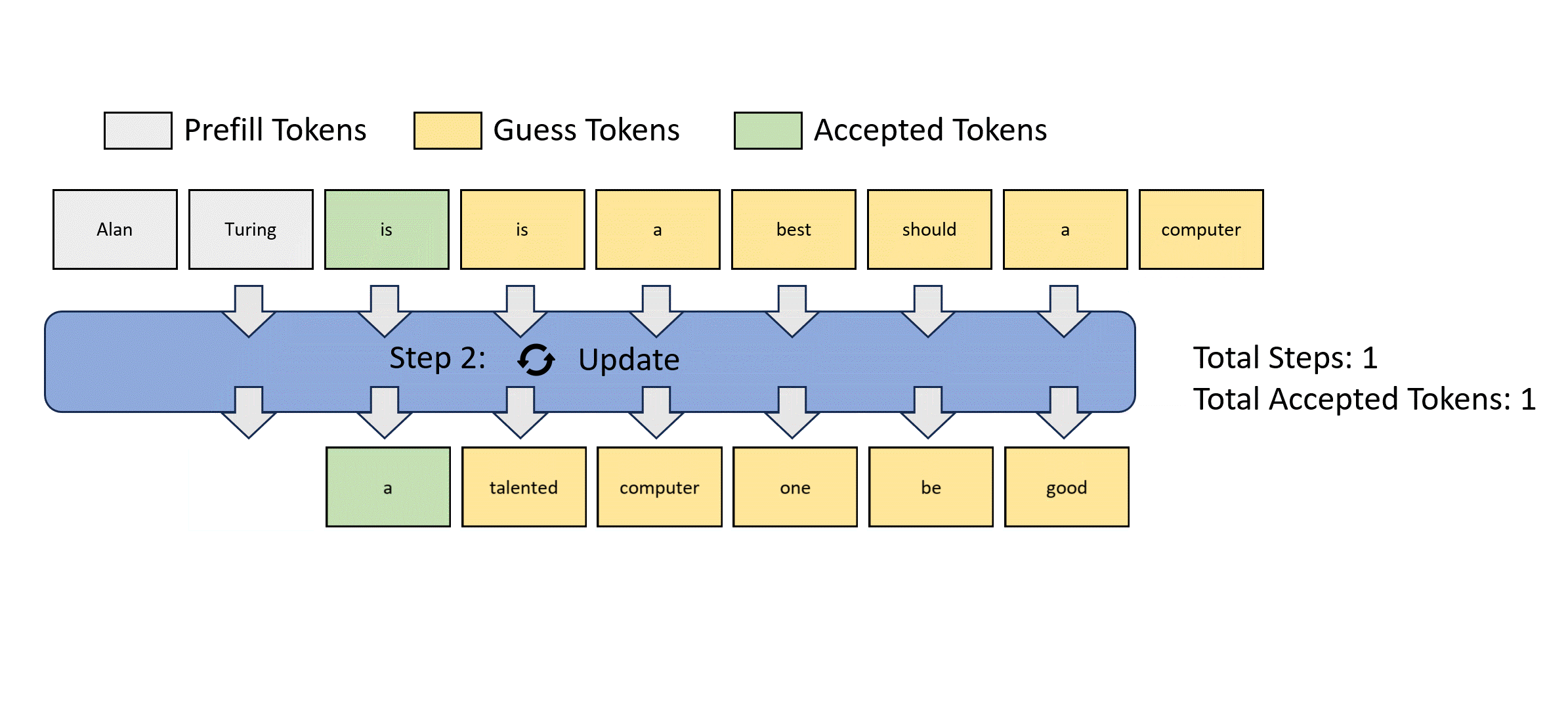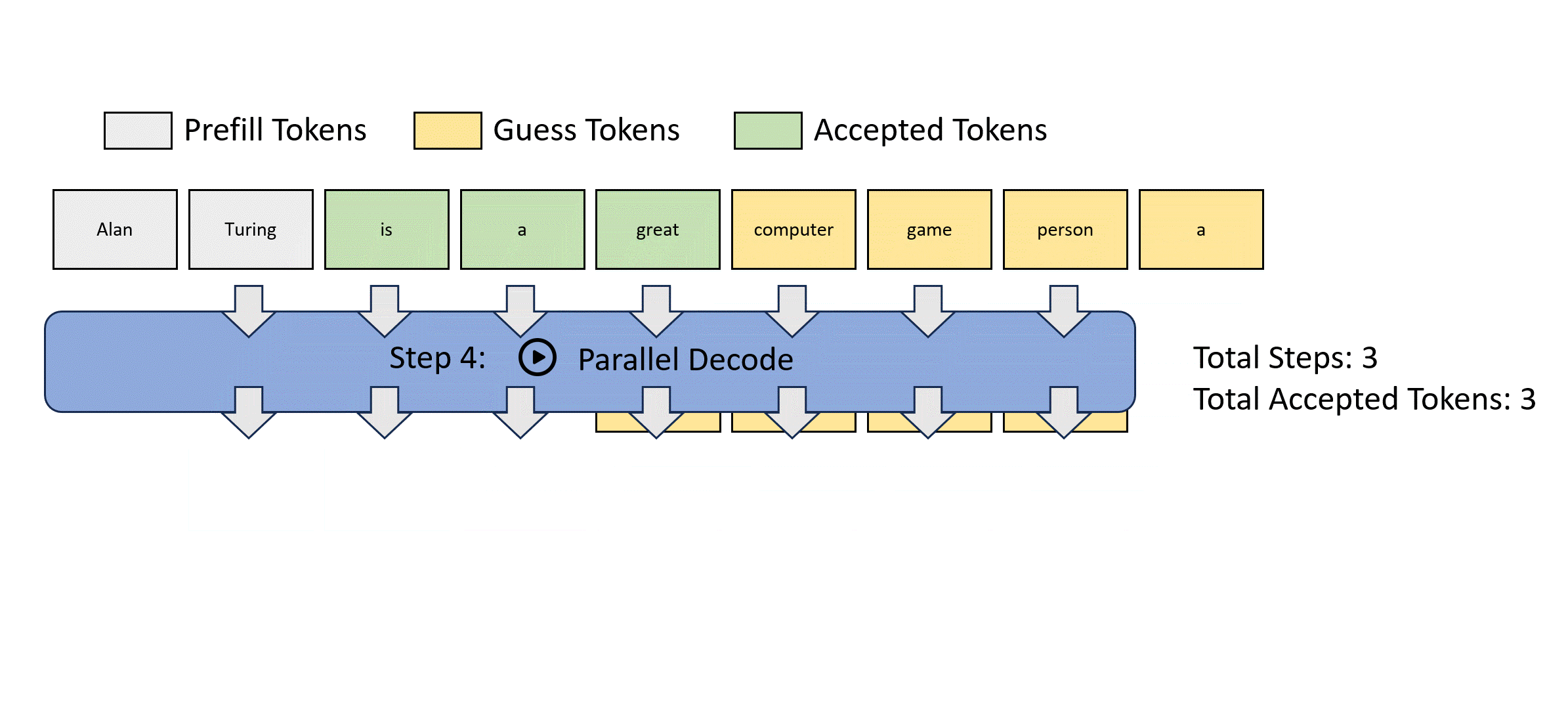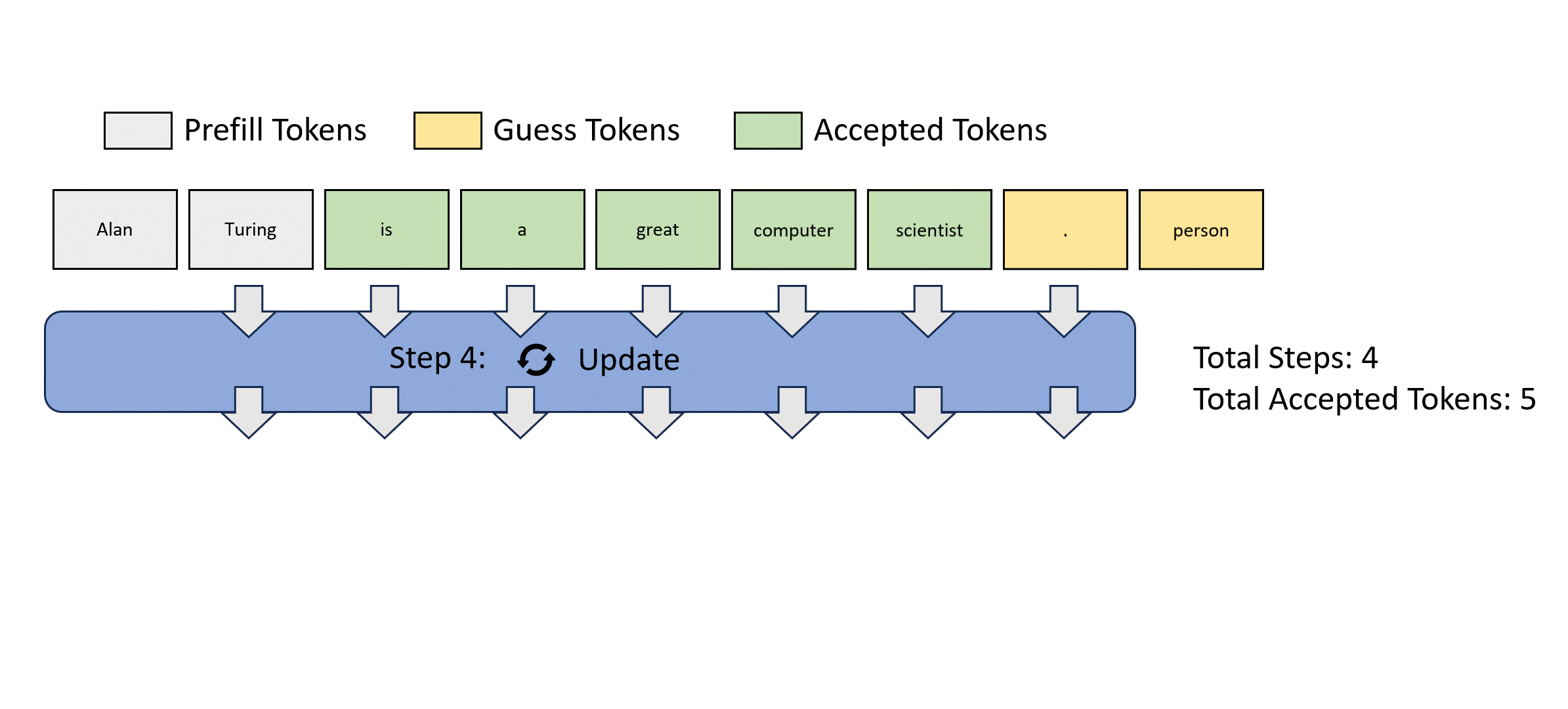
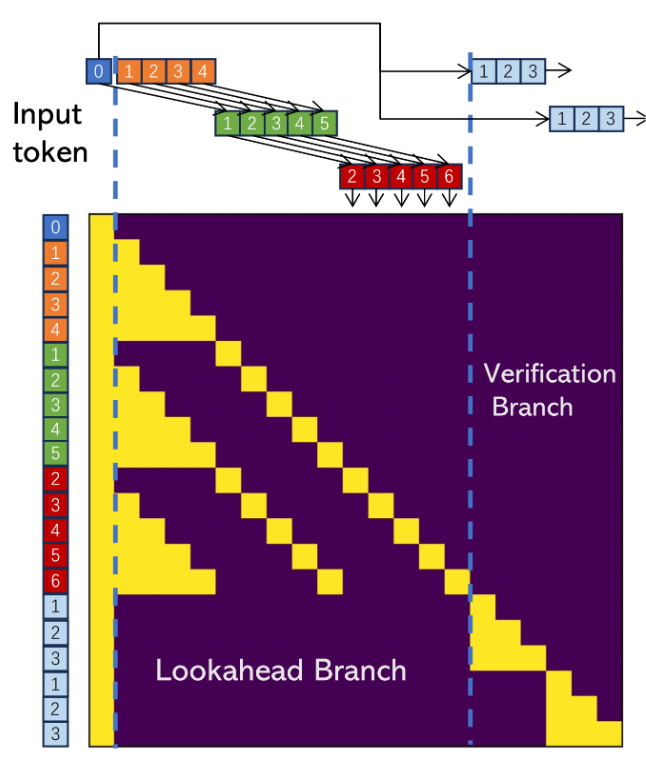
N-gram
- 2-gram to N-gram 可以幫忙 Jacob decode 更有效率?
Lookahead = Jacob + N-gram
Lookahead Branch + Verification Branch
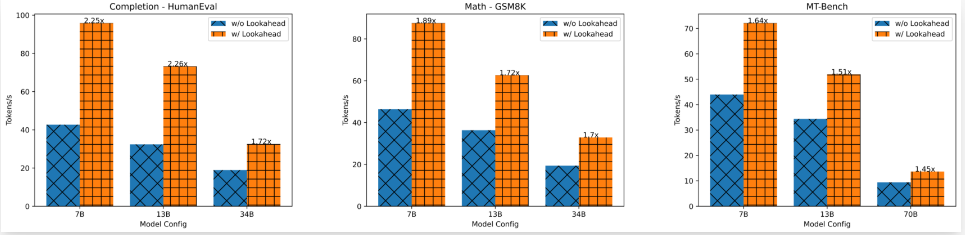
Speed Up
- 小 model 似乎效果最好。這和 speculative decode 剛好相反?
Reference
大语言模型量化方法对比:GPTQ、GGUF、AWQ - 知乎 (zhihu.com)
QLoRA——技术方案总结篇 - 知乎 (zhihu.com)
[@guodongLLMTokenizer2023]