Speculative Decode

Source

• Speculative Decoding with Big Little Decoder!!
  • https://arxiv.org/abs/2302.07863

• https://zhuanlan.zhihu.com/p/684217993: good 知乎 paper

• LLM推理加速新范式！推测解码（Speculative Decoding）最新综述-CSDN博客

• 2302.01318 (arxiv.org) nice explanation of the speculative sampling math!

• Speculative Sampling — Intuitively and Exhaustively Explained (substack.com) with code and example!!

• https://www.jinghong-chen.net/an-mathematical-intuition-of-speculative-sampling/ intuition of the accept with resampling!

• Cloud-edge hybrid SpD! [2302.07863] Speculative Decoding with Big Little Decoder (arxiv.org)

前言

Speculative Decoding 希望解決的是現有的 Autoregressive 模型推理過慢的問題。其思路很簡單：在一次前向傳播中，同時驗證多個 draft token。所以此技術的核心便在於如何儘可能又快又準地生成 draft token，以及如何更高效地驗證 (verification)。

目前的大語言模型 (LLM) 都是基於 auto-regression

重點是 sampling of conditional probability. 一般是用 greedy algorithm (溫度 T = 0), 就是取機率最高的 $x_{n+1} \sim \arg \max p(x \mid x_1, …, x_n)$​, 再重複同樣步驟。

如果 output 要有多一點變化或創意，可以把 T 上調到 0.8 或 1. 此時會根據機率分佈隨機取樣。

這是一個 sequential process. 要加速，就是要打破 sequence dependency, 並利用 parallel verification。用數學表達：

1. 生成一個 draft token 的時間, $t_1$, 遠小於生成 (也就是驗證) 一個真正 token 的時間, $T_1$, i.e. $t_1 \ll T_1$

2. 同時驗證 n 個 tokens 的時間接近驗證一個 token 的時間, i.e. $T_n \approx T_1$

Speculative Decoding 中最重要的技術有兩個：

​ A. Speculative Sampling

​ B. Tree Attention

因爲這是後續所有文章都會使用的兩個技術。

Speculative Sampling

先復習之前的 Math_Sampling 文章，如下。 $q(x)$ 是 target distribution, $p(x)$ 是 draft, proxy, proposal distribution.

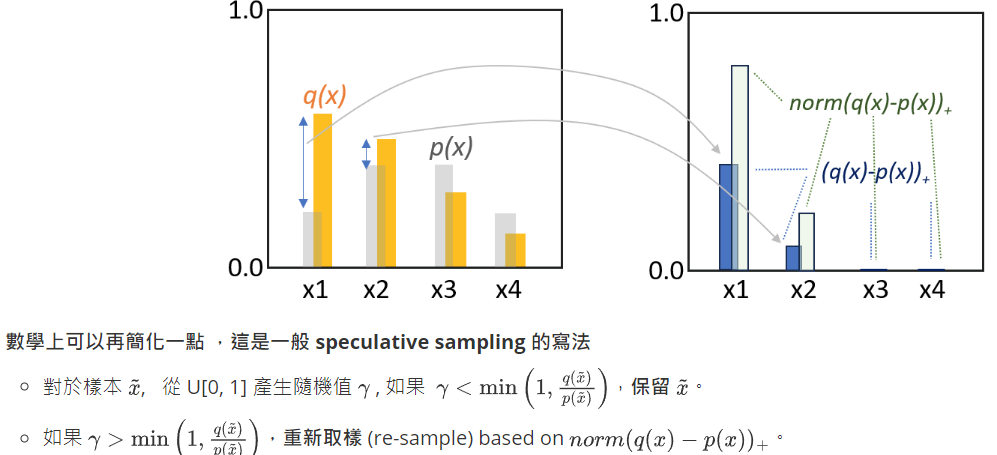
對比一下 speculative sampling 的寫法是否一致？YES!

數學證明見 Appendix。基本原理就是多退少補。前文 （Math Sampling）有比較詳細的說明！

Speculative Decode vs. Speculative Sampling

Speculative sampling 是用一個 draft distribution 逼近 target distribution 的取樣方法。

Speculative decode 一般是指 (1) 如何找出 draft distribution 且又快又準地生成 draft tokens; (2) 如何高效驗證 (verify) draft tokens.

Draft 產生的方式包含: (1) 獨立分離 drafting, 包含大小模型。 (2) 自我 drafting，包含 Medusa, SPEED, Lookahead.

Verification (驗證) 的方式包含: (1) Greedy decoding (T=0 取 maximum probability) 以及調整 T 的 sampling；(2) Nucleus sampling 或是 Top-k sampling 就是取前 k 大的機率 sampling; (3) Token tree verification, 這是用於 tree attention 的方法。

這是一個 sequential process. 要加速，就是要打破 sequence dependency, 並利用 parallel verification。用數學表達：

1. 生成一個 draft token 的時間, $t_1$, 遠小於生成 (也就是驗證) 一個真正 token 的時間, $T_1$, i.e. $t_1 \ll T_1$

2. 同時驗證 n 個 tokens 的時間接近驗證一個 token 的時間, i.e. $T_n \approx T_1$

Speculative Decoding 中最重要的技術有兩個：

​ A. Speculative Sampling

​ B. Tree Attention

SpD 有幾種方法

• (5.1/6.2) Draft model (小模型) + Target 模型: 技術是 A. 利用假設是 1 and 2.

• (5.2/6.3) Target 模型 + 多頭 Medusa: 技術是 A and B. 利用假設是 1 and 2. 亂槍打鳥

• (5.2/6.1) Target 模型 + Lookahead: 技術是 A and B. 利用假設是 2. 亂槍打鳥

• Target 模型 + early exit: 技術是 A. 利用假設是 2. 亂槍打鳥

加速比較

	Speculative Decode	Medusa	Lookahead Decode
Model	Small Draft + Large Native models	Large + Multihead	Large + Lookahread
Overhead	10%	7%	?%
Speed up	Depends on small model 大 model 最好	2x	小 model 最好？
Input	Sequential from draft model		Jacobe?
Output	Parallel verify		Parallel verify

Speculative Decoding 與 Speculative Sampling

Speculative Decoding: Exploiting Speculative Execution for Accelerating Seq2seq Generation

[paper] [paper reading]

第一篇提出 Speculative Decoding 這個詞的文章，確立了使用 draft-then-verify 這一方法加速 Auto-Regressive 生成的範式。

Speculative Decoding 希望解決的是現有的 Autoregressive 模型推理過慢的問題。其思路很簡單：在一次前向傳播中，同時驗證多個 draft token。在第一個 draft token 與原始模型輸出不相符的位置截斷，並丟棄在此之後的所有 draft token。

作者在 draft 這一步使用的是一個另行訓練的模型。這裏作者確立了 Drafter 的兩個原則：Capability Principle（儘可能準）和 Latency Principle（儘可能快）。作者這裏採用的辦法是增加 Encoder 層數，減少 Decoder 層數，從而在不太影響性能的同時降低響應時間。（作者主要關心的是機器翻譯這個任務用的是 encoder + decoder，而不是 decoder only，而且沒用很大的能稱得上 LLM 的模型）

在 verify 階段，作者放寬了必須和原模型輸出完全一樣的限制，只要在 top-𝛽 candidates 之內且和 top-1 的似然的 gap 不超過閾值 𝜏 便接受。這裏一方面是爲了接受率和加速比考慮，另一方面是本文設定下的 Drafter 並不一定比原模型差，所以適當接受 Drafter 的異見並不會犧牲性能。

實驗都是在機器翻譯的數據集上做的。作者使用的原模型是 6 層 Encoder 加 6 層 Decoder 的 Transformer，Drafter 是 12 層 Encoder 加 2 層 Decoder。結果是達到了 5 倍的加速比。

這篇文章的受關注程度是和後續幾篇文章不成正比的。我個人想到了以下幾點原因：

1. 從時間上來看，Google 的那篇和後續 DeepMind 的那篇我認爲是有故意不引用的嫌疑的。
2. 本文解決的問題侷限性太強了，只做了機器翻譯的相關實驗。Google 那篇做了四個生成類任務：機器翻譯、文本總結、1m1b文本生成、對話。
3. 本文沒有使用特別大的模型，可能會使得關注度沒有那麼高。Google 那篇最大用到了 137B 的 LaMDA。
4. Google 那篇的 Figure 1 很抓人眼球，一張圖就把整個 idea 講明白了。這個確實是個很大的優勢。
5. 從技術角度，Google 的方法保證了最後的生成結果和原模型的輸出完全一致，並提供了理論證明。對於 LLM 的加速來說，這確實比本文的 verify 在生成質量上更有保障。

但不管怎麼說，Google 那篇引用量是本文的十倍仍然是一件很奇怪的事情。如果 Google 那篇正確引用了本文，那或許就會不太一樣了。

(Google) Fast Inference from Transformers via Speculative Decoding

[paper] [paper reading]

這篇被很多人錯認爲是 Speculative Decoding 的開坑之作。

不討論學術道德的問題，但就論文本身，這篇文章確實寫得相當棒。

首先就是這個 Figure 1，非常簡潔直觀。本文用 target model（目標模型）指代待加速的大模型，用 approximation model（近似模型）指代用來幫助加速大模型的小模型。

綠色token：近似模型提出且目標模型接受的建議；紅色token：近似模型提出但目標模型拒絕的建議；藍色token：目標模型對於紅色token的訂正

之後是本文最重要的技術：Speculative Sampling。這個方法的可以兼容不同的採樣策略。具體步驟如下：

1. 首先介紹一下 notation：我們有前綴 $x_{<t}$，我們希望生成 $x_t$，目標模型輸出分佈爲 $q(x_t \vert x_{<t})$，簡記爲 $q(x)$，draft 模型的輸出分佈爲 $p(x_t \vert x_{<t})$，簡記爲 $p(x)$。再次強調 $p(x), q(x)$ 都是條件機率。
2. 取 $x \sim p(x)$，如果 $p(x) \le q(x)$ 則保留 $x$，如果 $p(x) > q(x)$ 則以 $1 - \frac{q(x)}{p(x)}$ 的機率丟棄 $x$。
3. 對於丟棄的 $x$，我們以 $q’(x) = norm(\max(0, q(x)-p(x)))$​ 的機率重新採樣。

可以證明經過這樣的採樣步驟，$x \sim q(x)$，以下是簡略的證明思路：

對於給定的輸出 $x’$，存在兩種可能： draft 模型的輸出被接受了，這個機率爲 $p(x’) \min\left(1, \frac{q(x’)}{p(x’)}\right)$； draft 模型的輸出被拒絕了，重新採樣得到了 $x’$，這個機率爲 $ \left(1 - \Sigma_x p(x) \min\left(1, \frac{q(x)}{p(x)}\right)\right) q’(x’)$。可以計算得二者相加爲 $q(x’)$。

特別指出，如果目標模型用的是 argmax 之類的 sampling 方法，那麼可以把 $q(x)$ 視爲 one-hot 分佈，那麼這就和最樸素的 Speculative Sampling 一致了。這其實就是 Greedy decoding.

之後作者用計算機多級流水的類似思想證明了一些和近似模型輸出接受率相關的結論，也討論了近似模型應當輸出多長的序列。

實驗部分，作者用 11B 的 T5-XXL 爲目標模型，做了英-德翻譯和文本總結兩個任務；用 97M 的 GPT-Like 模型爲目標模型，做了 1m1b 的文本生成任務；用 137B 的 LaMDA 爲目標模型，做了對話任務。

Accelerating Large Language Model Decoding with Speculative Sampling

[paper]

這篇和 Fast Inference from Transformers via Speculative Decoding 的貢獻一模一樣，提出的 Speculative Sampling 在細節上也是一樣的。實驗上會有區別，用的是 70B 的 Chinchilla 做目標模型，4B 的模型做 Draft Model，主要做了文本總結和代碼生成的任務。

Tree Verification

SpecInfer: Accelerating Generative Large Language Model Serving with Tree-based Speculative Inference and Verification

[paper] [paper reading]

本文把小的模型叫 SSM（Small Speculative Model），大的模型叫 LLM。

本文有兩個貢獻點：1. 使用了多個 SSM，並使用了類似集成學習的方法使多個 SSM 的輸出儘可能覆蓋 LLM 的輸出；2. 使用了一種基於樹的 Speculative Inference，使得在一次 inference 中可以完成對多個猜測的輸出 sequence 的驗證

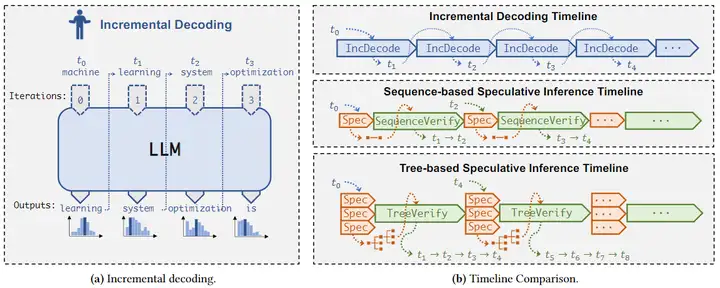
SSM 的訓練是用了類似於 boost-tuning 的方法：每次只訓練一個 SSM，當 SSM 訓練完成後，將訓練集中這個SSM 的輸出與 LLM 輸出一致的那些訓練數據刪去，並用剩下的訓練集繼續訓練下一個 SSM。這樣，多個 SSM 的輸出可以儘可能地覆蓋到 LLM 可能的輸出。

在 Speculative Inference 階段，作者先爲每個 SSM 生成了一棵輸出樹，即在每個 token 取若干種可能性構成一棵樹，之後將這些樹合併成一棵更大的樹。

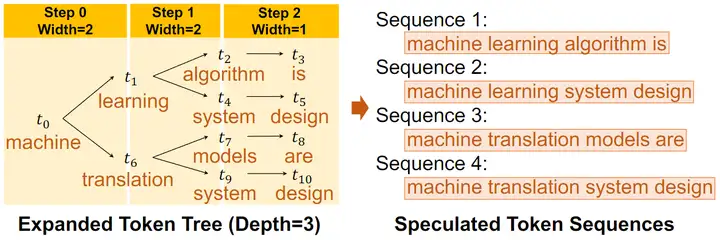
之後便是將生成的樹進行驗證。這裏作者通過改變 mask 矩陣，使得模型可以一次驗證多個 sequence。如下圖所示，對於這樣一棵樹，如果採用常規的 mask 方式，t6 是可以看到 t5 的，但在圖示的 mask 矩陣下，每個 token 只可以看到自己的 prefix，從而使得 LLM 可以一次完成對於多個 sequence 的不互相干擾的驗證。

之後作者參考谷歌那篇的 Speculative Sampling，提出了 Multi-Step Speculative Sampling。作者證明了 Multi-Step Speculative Sampling 的採樣與直接從 LLM 採樣等價，且 Multi-Step Speculative Sampling 的採樣通過率更高（前者在前文也有類似證明，但後者似乎是本文最先證明的）。

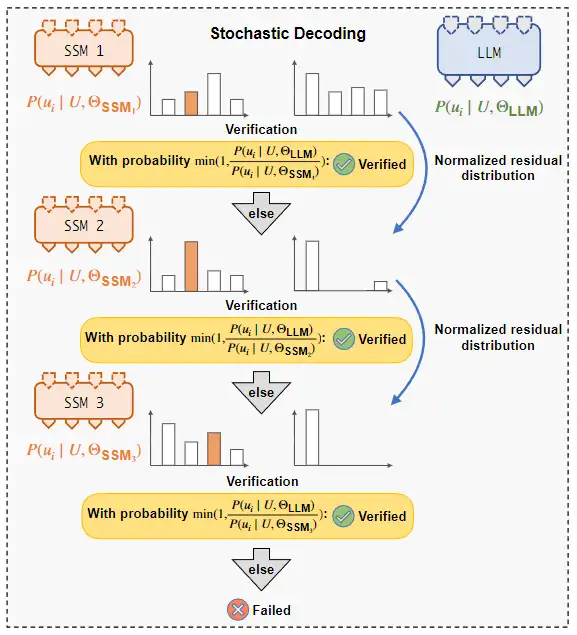
總體流程大致如下圖所示：

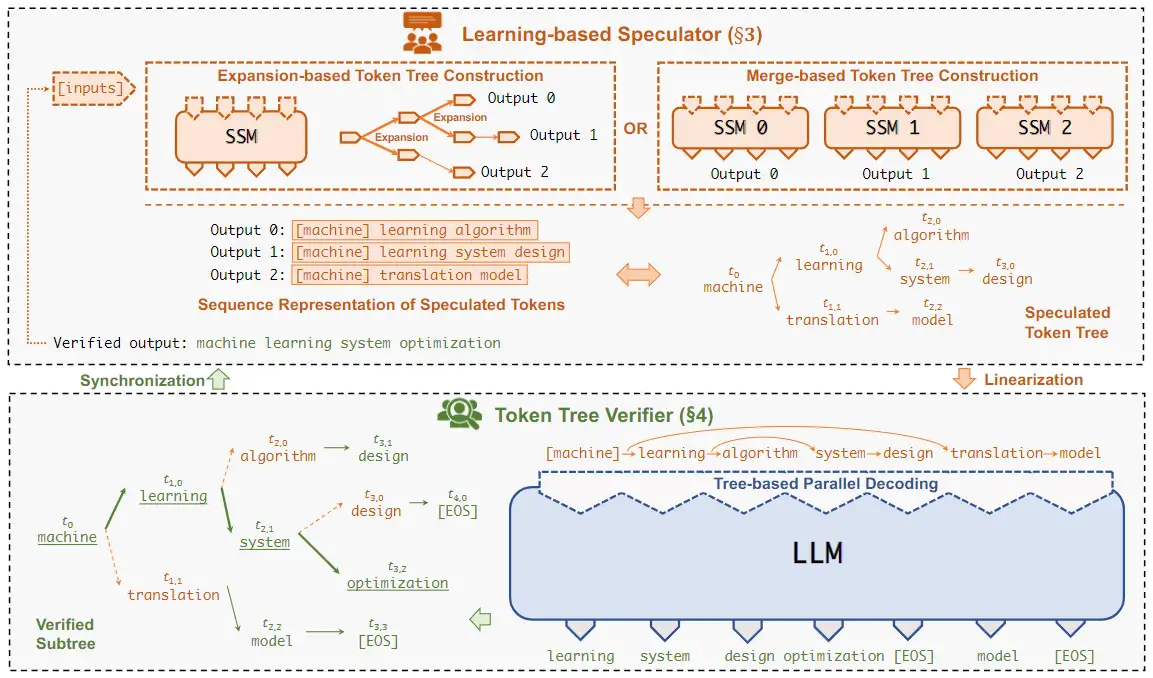
實驗部分，本文主要驗證的是對話任務，使用了 LLaMA-7B, OPT-13B, OPT-30B 和 LLaMA-65B 作爲 LLM， LLaMA-68M 和 OPT-125M 作爲 SSM。

Sequoia: Scalable, Robust, and Hardware-aware Speculative Decoding

[paper] [paper reading]

本文的最大的創新點是 Tree Verification 時樹的構建。本文的有趣之處在於，先定好樹的結構，然後往裏面填 draft token。

樹的具體構建方法基於 positional acceptance assumption：接受某個已接受 token 的預測機率第 𝑘 大的後繼 token 的機率只取決於 𝑘 ，設爲 𝑝𝑘 。每個子節點的得分爲從根節點到此節點的所有 𝑝𝑘 相乘。最後的目標是在給定節點數量的情況下使整棵樹所有節點得分相加最大。

這個問題的解可以用更小的子問題的解來表示，因此此問題可以通過動態規劃求解。求得的樹結構會滿足預測機率較大的子節點會有更多的子孫。所以本文使用的樹結構大致如下圖（從本文的博客裏找到的圖）：

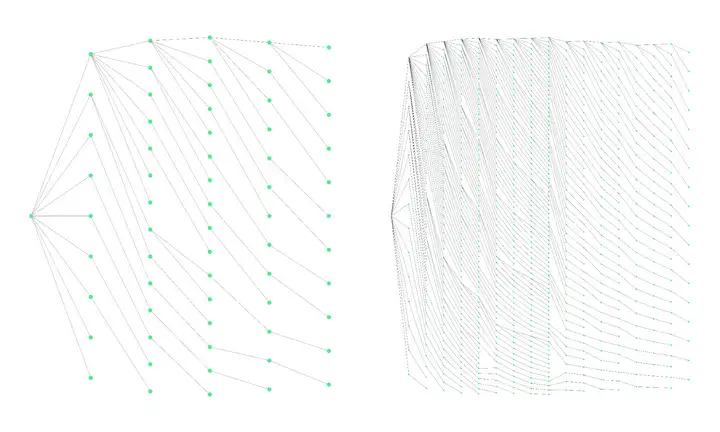
之後便往這樣的樹結構裏填空 draft model 的輸出。Sequoia 會進行無放回的採樣。在填充同一子樹的同層子節點時，會將已經採樣過的節點機率歸零。

作者對 Sequoia進行一些理論分析。作者定義了兩個屬性：optimal transport 屬性和 cover 屬性：

1. 所謂 optimal transport，是指根據 SpecTr 這篇文章指出，預測 token 只有一個的時候，接受率在最優傳輸的情況下爲 1−‖𝑃−𝑄‖12 （ 𝑃 和 𝑄 分別爲兩個模型的輸出機率）。
2. cover 屬性指的是 draft model 的輸出不爲零的 token 可以覆蓋 target model 的所有輸出可能性。

作者指出，一般的 Tree Verification 方法只滿足 optimal transport 屬性，而樸素的 top-k sampling 只滿足 cover 屬性。而 Sequoia 同時滿足兩個屬性，因而可以如下圖所示在不同的溫度下都表現良好。

• 當溫度較小的時候，輸出較爲 sharp，此時 target model 的輸出候選集一般是會小於 draft model 的，Sequoia 採用無放回採樣就會導致總會選到 target model 的輸出，而之前的有放回採樣方法就存在一直選不到 target model 的輸出的可能性。
• 而溫度較大的時候，輸出較爲平滑，此時 top-k sampling 表現會嚴重下滑，而採用了 Speculative Sampling 的 Tree Verification 方法（包括 Sequoia）會表現良好。

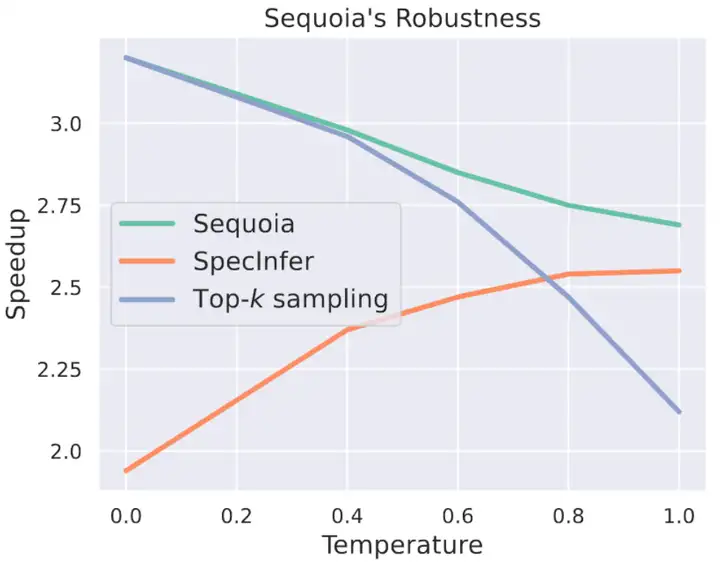
Sequoia 還會爲不同的硬件選取不同的樹節點數和深度限制，從而使得本算法可以很好地適應不同的硬件。

關於實驗部分，值得一提的是，在一般的設置之外，本文還跑了 offload inference 的設置。當沒有了顯存和帶寬的限制，Tree Verification 顯示出了恐怖的加速比：SpecInfer 可以跑到 5x 左右的加速比，本文可以跑到 8x 左右的加速比，最高可以到 9.96x 的加速比。

原模型+新預測頭 作爲 Draft Model

Medusa: Simple LLM Inference Acceleration Framework with Multiple Decoding Heads

[paper] [paper reading]

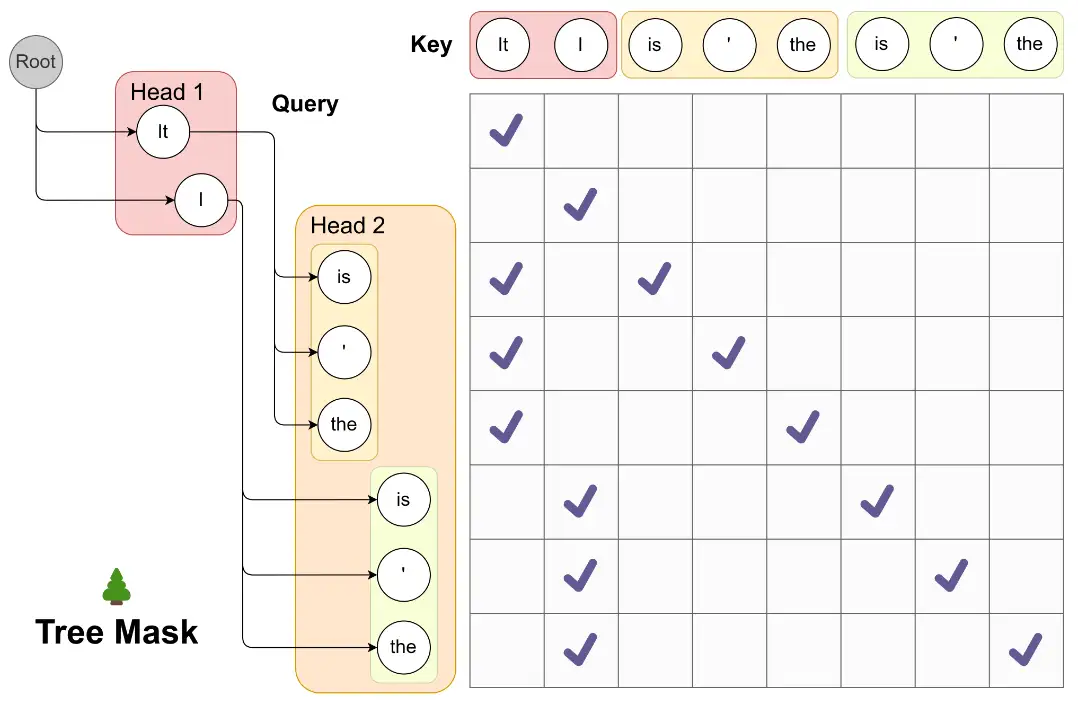
Medusa 和 SpecInfer 一樣採用了 Tree-based Attention，但這裏沒有使用小模型作爲 Draft Model，而是在原模型的最後一層加了若干個 Medusa Head，第 𝑖 個 Medusa Head 負責預測當前預測 token 之後的第 𝑖 個token。每個 head 取 top-k 的預測，將這些預測的 token 取笛卡爾積，即可得到若干候選 sequence。

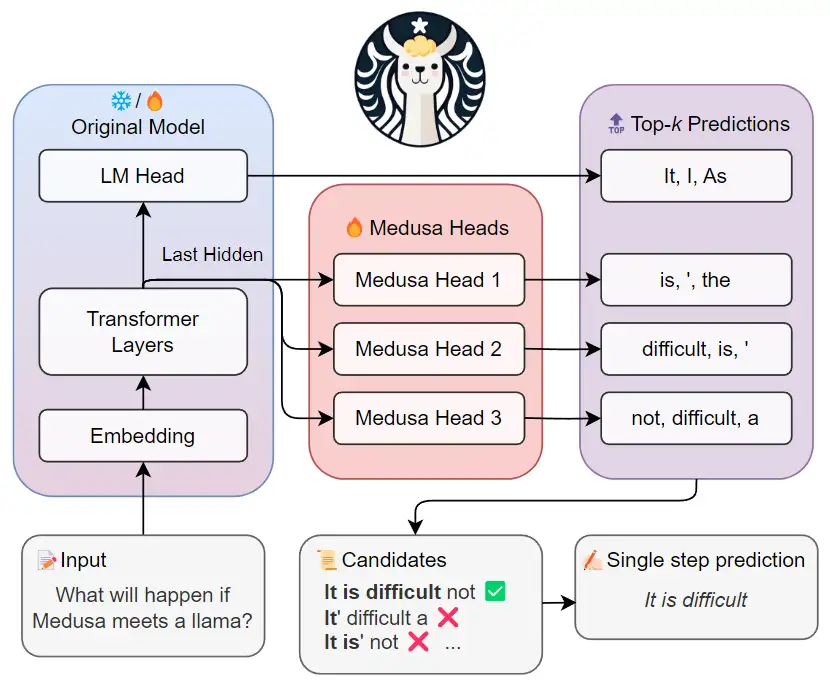
這些 sequence 構成了一棵樹。通過 tree mask 的方法，在下次 inference 的過程中，模型可以一次驗證多個 sequence。爲了區分不同的 prefix，本文設置了一些冗餘，例如 Head 2 的三個預測 token 均出現了兩次，這是爲了分別對應 It 和 I 這兩個不同的 prefix。每個 token 在 tree mask 的作用下只可以看見自己的 prefix。

對於這些 Medusa Head 的訓練，作者提供了兩種策略。第一種是凍結原模型參數只訓練 Medusa Head。因爲靠後的 Head 會更加的不確定，爲了平衡各個 Head 上 loss 的大小，作者設置了一個指數衰減的權重。第二種是原模型和 Medusa Head 一起訓練。作者將原模型的 loss 與訓練 Medusa Head 的 loss 相加之後，爲 Medusa Head 設置了更大的學習率，併爲這些 Head 做了 warm up。

之後作者還提供了三個進一步提升性能的工具。

1. Typical Acceptance 之前有工作指出，在加大溫度的時候， Speculative Decoding 的效果會變差。作者認爲，加大問題的作用就是增加輸出的多樣性，因此此時不必一定要與原模型的輸出對齊。作者將超過一定機率閾值的 token 及其 prefix 保留。當前步驟的最終預測由所有候選中最長的可接受 prefix 來確定。
2. Self-Distillation 這個不多說，對齊了原模型的預測機率和 Medusa Head 的預測機率。
3. Searching for the Optimized Tree Construction 樹的規模會很大。作者爲了減小樹的尺寸，用一個校準數據集記錄了每個節點預測正確的機率，之後用貪心法保留了預測最準確的節點。

實驗部分，作者跑了 Vicuna-7B、13B、33B 和 Zephyr-7B。

Hydra: Sequentially-Dependent Draft Heads for Medusa Decoding

[paper] [paper reading]

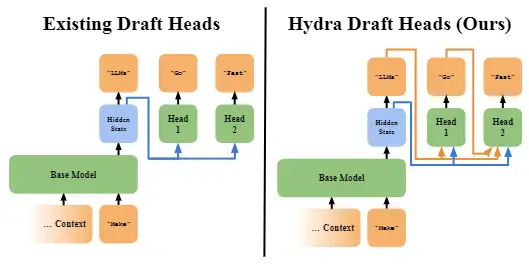
在 Medusa 的基礎上做的改進，增加了 draft head 預測之間的關聯性。最基礎的 Hydra 已經可以在 Medusa 的基礎上有 1.1x 的加速。

作者可能是覺得這個貢獻不太夠？於是又提出了 Hydra++，加了幾個新 trick，最終能達到相對於 Medusa 有 1.31x 的加速比：

1. 爲輸入序列加噪聲
2. 使用 base model 的輸出預測機率作爲知識蒸餾的教師模型輸出來訓練 draft head
3. 增加一個獨立的 decoder layer，每個 Hydra head 除了上一個 token 本身，還添加了上一個 token 在這個 decoder layer 的 representation 作爲輸入（合理懷疑這就是借鑑了 EAGLE，雖然作者在文章最後聲明自己和 EAGLE 是同時的文章）

Jacobi Decoding 及其衍生方法

Accelerating Transformer Inference for Translation via Parallel Decoding

[paper] [paper reading]

本文提出了 Jacobi Decoding，是 Lookahead Decoding 和 CLLM 的前驅工作

本文的思路是把 Autoregressive 的過程看作是聯立以下方程求方程組的解的問題：

{𝑦1=arg⁡max𝑝𝜃(𝑦1

𝑥)𝑦2=arg⁡max𝑝𝜃(𝑦2

𝑦1,𝑥)⋮𝑦𝑚=arg⁡max𝑝𝜃(𝑦𝑚

𝑦1:𝑚−1,𝑥)

那麼普通的 Autoregressive 解碼過程就相當於每次都將上一式解出之後帶入下一式。而作者想到了直接使用自行迭代的方法尋找方程組的解。因爲是 Greedy Decoding，所以每次迭代至少能獲得一個穩定的 token ，因而迭代的次數 𝑘≤𝑚 。

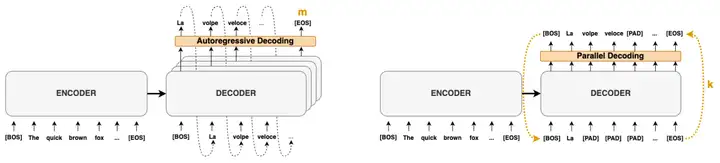
技術細節上，既可以整體迭代，也可以分塊迭代。考慮到機器翻譯的任務當中有 符號，本文還提出了混合式解碼法，遇到 之後就恢復到 Autoregressive 解碼。

本文的一大缺陷是只適用於 Greedy Decoding。

Break the Sequential Dependency of LLM Inference Using Lookahead Decoding

[paper] [paper reading]

本文是 Accelerating Transformer Inference for Translation via Parallel Decoding（即 Jacobi Decoding） 的一種推廣。

本文將 Jacobi Decoding 視爲本文在 2-gram 情況下的特例。Jacobi Decoding 將每次迭代上一次的輸出整體作爲下一次的輸入，其實就是把每一個 token 上的輸入輸出視作一個 2-gram 作爲 Draft Model。作者想到，如果可以記錄下更多的歷史信息，就可以製造一個 N-gram 作爲 Draft Model，這樣就可以提高 Speculative Decoding 的準確率。

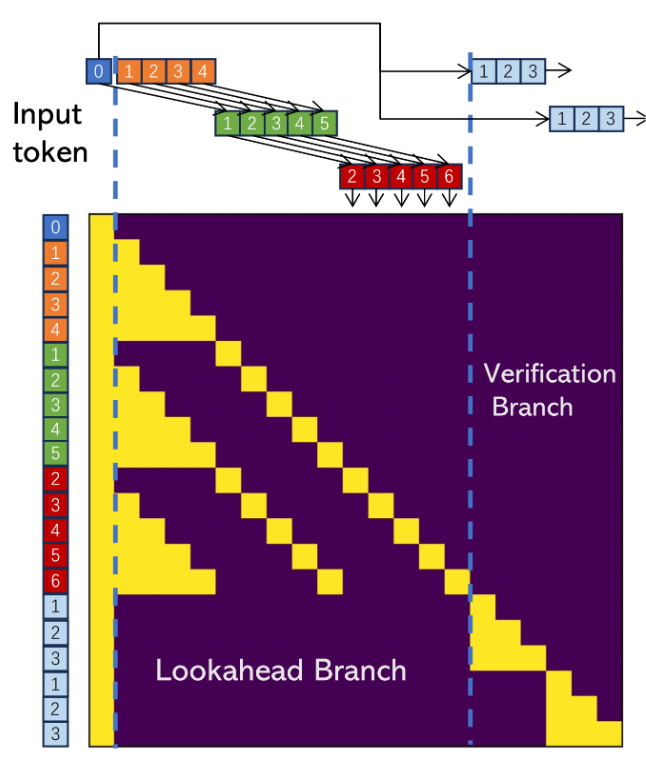
本文提出的 Lookahead Decoding 在一次前向傳播過程中完成了兩件事：生成 N-gram 歷史信息（Lookahead Branch）和 選取合適的 N-gram 歷史信息進行 verification（Verification Branch）。圖中，藍 0 指的是 prompt 與之前已確定輸出的最後一位。這裏取 window size 𝑊=5 ，N-gram size 𝑁=4 ，verification 數量 𝐺=2 。

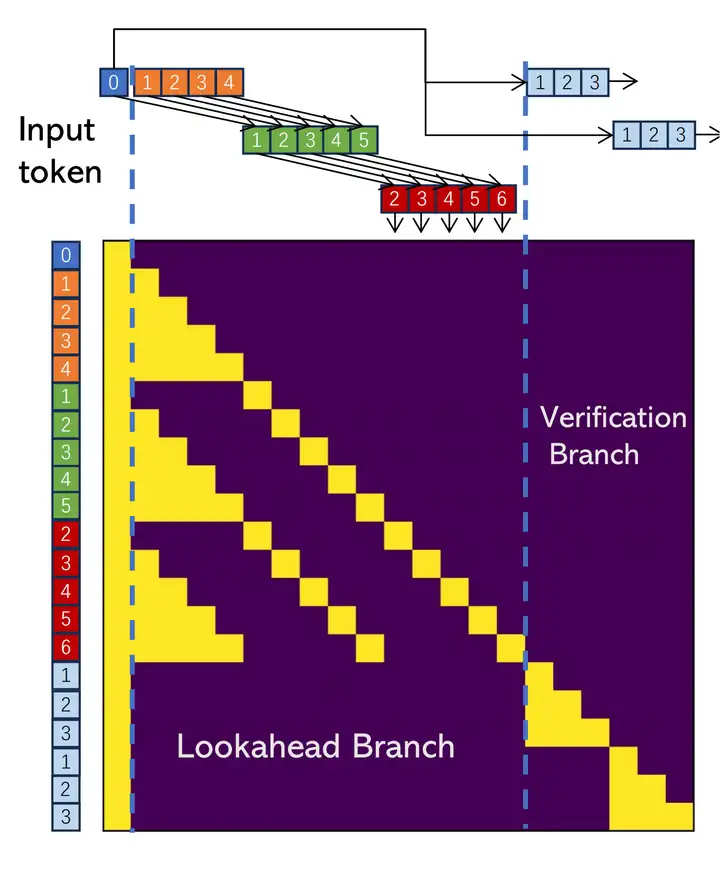
Lookahead Branch 裏，同種顏色的表示是同一次前向傳播裏一起生成的 token。在上圖中，綠 1~5 是 橙 0~4（圖中沒有 橙 0 是因爲 橙 0 被模型的正確輸出 藍 0 取代）在上上次前向傳播的輸出，紅 2~6 是 綠 1~5 在上次前向傳播的輸出。假設本次得到的輸出是 灰 3~7，那麼將 [藍 0，綠 1，紅 2，灰 3]，[橙 1，綠 2，紅 3，灰 4]，[橙 2，綠 3，紅 4，灰 5]，[橙 3，綠 4，紅 5，灰 6]，[橙 4，綠 5，紅 6，灰 7] 加入到 N-gram Pool 中。在下一次前向傳播的輸入裏，在當前 藍 0 的輸出（姑且稱之爲 藍 1）之後，Lookahead Branch 裏就應該是 綠 2~5，紅 2~6，灰 3~7。

關於 Lookahead Branch 裏這些序列的初始生成，最好翻看一下源代碼。以下圖爲例，作者先在給定 prompt 之後隨機生成了 𝑊+𝐻−3 （5 + 4 - 3 = 6）個 token（即 橙 1~6），將 prompt 和這些 橙 1~6 一併作爲輸入。在第一次前向傳播後，將 橙 1~6 的輸出（即 綠 2~7）加在現有的輸入之後，並用 prompt 最後一位的輸出（藍 1）替代 第一次添加的輸入的第一位（橙 1）。接下來進行第二次前向傳播，將 綠 2~7 的輸出 紅 3~8 繼續添加到輸入裏，並用 藍 2 替代 橙 2 作爲第三次的輸入。

在得到第三次前向傳播的輸出後，我們便完成了 Lookahead Branch 的搭建。之所以還畫出了第四次前向傳播，是爲了方便讀者觀察 Lookahead Branch 的搭建到正常運行中間的細微差別。

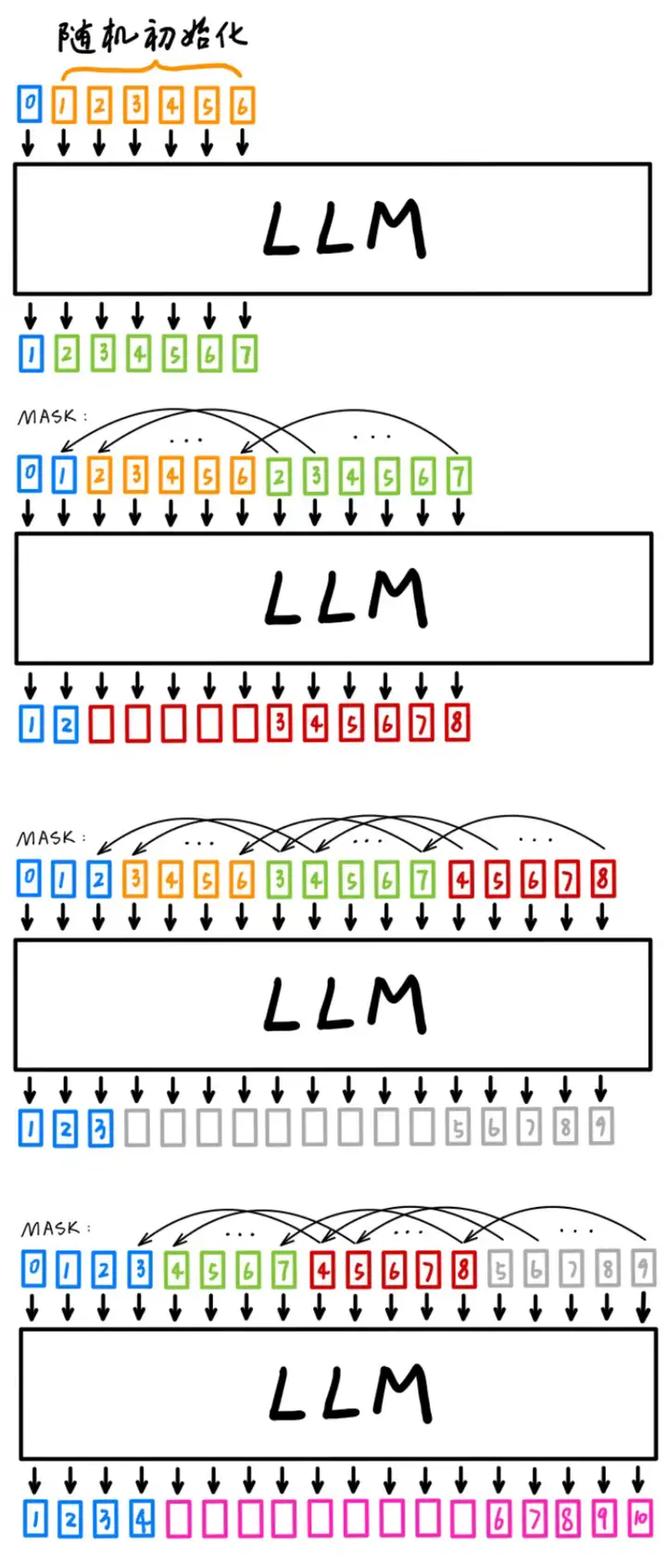
Lookahead Branch 需要 𝑁−2 次前向傳播才能完全搭建好。在此之前， N-gram Pool 爲空，此時是沒有 Verification Branch 的。

Verification Branch 裏所選取的樣本很簡單，是直接在 N-gram Pool 裏選取第一位是 藍色 token 最後一位的 N-gram。這其中驗證之後被接受的即可作爲本次的輸出，若全部沒有接受在輸出 藍色 token 最後一位的輸出。

本文還提到了一個小的技術細節：在分佈式訓練的過程中，可以將 Verification Branch 放在 Lookahead Branch 的長度較小的機器上，達到負載均衡的效果。

實驗部分，作者使用了 7B、13B、34B 和 70B 的 LLaMA-2 和 CodeLLaMA。

Ouroboros: Speculative Decoding with Large Model Enhanced Drafting

[paper] [paper reading]

本文可以算是 Lookahead Decoding 的 draft-target 分離版與性能加強版。本文的核心還是 candidate pool。

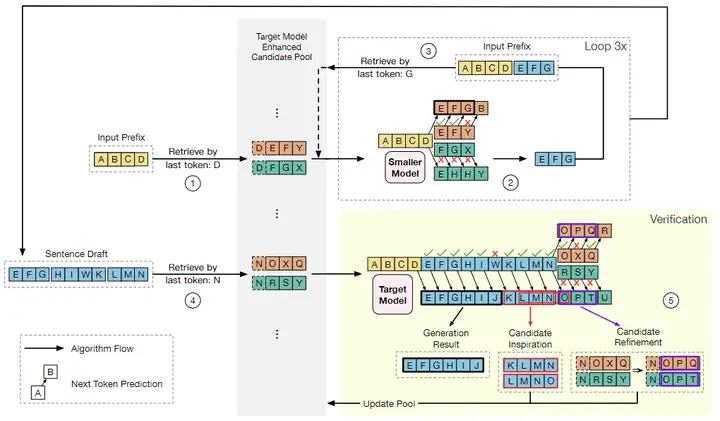
給定輸入前綴 ABCD，假設 target model 會生成 EFGHIJKLMN，而 draft model 輸出EFGHIWKLMN。

1. 在每次迭代中，我們首先使用最後一個 token（在本例中爲D）在 candidate pool 中檢索可能緊挨着 D 的一些候選輸出。
2. 使用 draft model 來驗證這些候選輸出，並且在校正之後，生成序列EFG。
3. 以上過程執行多次，其中 EFG 生成 HIWK ，EFGHIWK 生成 LMN。
4. 之後，基於 draft model 生成的序列被組合成 draft：EFGHIWKLMN，並且以 candidate pool 中以最後一個 token N 開始的組合作爲草稿後綴。
5. target model 同時驗證它們。
   1. target model 發現 I 的下一個標記應該是 J 而不是 W，這樣 EFGHIJ 就可以用作生成。
   2. W 之後的那些 draft token，即 KLMN，不能在當前迭代中用作生成，因爲它們基於錯誤的上下文 W。然而，由於它們與 target model 的輸出高度匹配，我們可以生成高質量的候選 KLMN 和 LMNO，這可以給EFGHIJ之後的 candidate pool 帶來啓發。
   3. 低質量候選後綴 NOXQ 和 NRSY 由目標模型固定，分別更改爲 NOPQ 和 NOPT。這兩個後綴都獲得了至少一個校正的 token，這有助於在未來的迭代中加快生成速度。

以上就是一個完整的 Ouroboros 執行過程。

作者在後續還增加了一個 warm start，就是在啓動階段直接用之前 decoding 過程中生成的 candidate pool，這樣可以緩解使用 candidate pool 的方法在起始階段 candidate pool 爲空的窘境。

將本文和 Lookahead Decoding 相比較，我總結了幾處有趣的改進：

• 首先是 draft model 與 target model 的分離。使用更小的 draft model 以生成更長的 draft token 序列。這打破了 Lookahead Decoding 單次驗證最多隻能驗證長度爲 N-gram 中的 N 的侷限性。
• 與 Lookahead Decoding 相比，N-gram 的生成經濟實惠的多。 Lookahead Decoding 的 lookahead branch 非常的奢侈，整個 branch 佔據了大量的輸入篇幅，卻只有最後幾個輸出的 token 有用。同時， Lookahead Decoding 的 verification branch 也沒有把被否掉的輸出廢物利用起來。本文的方法就很好地解決了上述兩個問題。
• Candidate Refinement 訂正了原有 candidate pool 中某些候選後綴，這一方面會縮減 candidate pool 的大小（因爲不然的話是直接加進去），另一方面會幫助剔除 candidate pool 中某些與眼下的生成關聯度不大的候選後綴。
• warm start 其實有一點點賴皮，但又很合理。有點好奇 Lookahead Decoding 加上 warm start 會是什麼結果。

CLLMs: Consistency Large Language Models

[paper] [paper reading]

本文基於的是 Jacobi Decoding，也就是 Accelerating Transformer Inference for Translation via Parallel Decoding 這篇文章中提出的方法。大致思路是 LLM 輸出（在 Greedy Decoding 下）是一個不動點，通過 LLM 不斷的自我迭代能用更少的次數找到這個不動點。作者把這樣的一個迭代過程看作了一個軌跡：

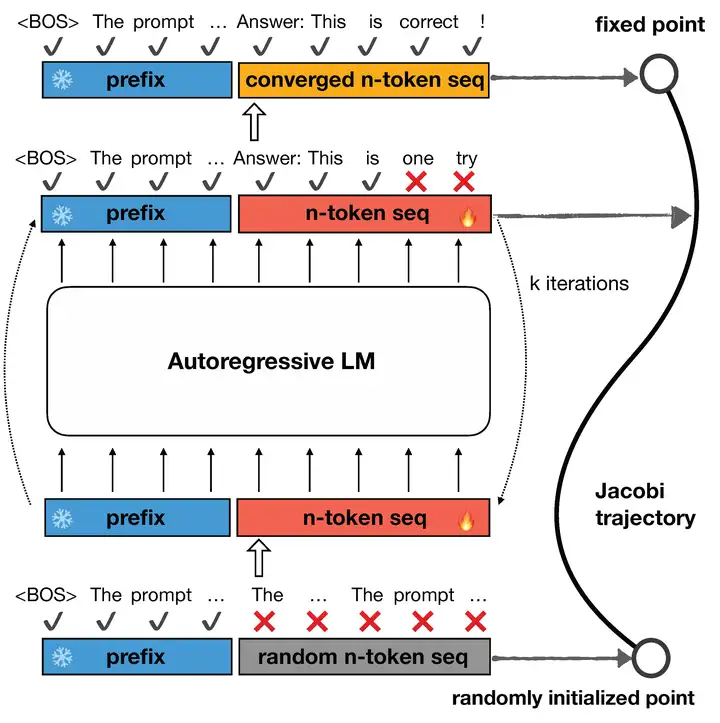
於是作者從 Consistency Model 得到了啓發，努力使 LLM 的 Jacobi trajectory 更短。作者在正常自迴歸模型的訓練損失之外引入了 Consistency Loss。Consistency Loss 分爲 Global Consistency Loss 和 Local Consistency Loss。其中，Global Consistency Loss 試圖使初始狀態的輸出與最終得到的不動點接近，而 Local Consistency Loss 試圖使 Jacobi trajectory 上兩個相鄰狀態的輸出更接近。具體公式參見本文的 blog 對應章節。

這樣訓練得到的模型會與原模型有所不同，因而與無法其它 Speculative Decoding 方法相比，只能和把原模型一起 finetune 的 Medusa2 相比。

特徵層 Speculative Decoding

EAGLE: Speculative Sampling Requires Rethinking Feature Uncertainty

[paper] [paper reading]

本文創新性地將 Speculative Decoding 前移至了特徵層（即倒數第二層）。這裏作者提出了兩個動機：

1. 特徵層的輸出相較於 token 層，更有規律性。（這點我感覺沒說明白，作者給了這個結論之後就說所以這樣效果會更好云云）
2. 保留特徵層可以更好的克服採樣過程中的不確定性。如下圖，在輸出 I 之後，會按機率採樣輸出 am 或是 always。在進一步尋找 always 的後續輸出時，如果能保留 I 的特徵層輸出，就能保留住採樣過程中丟掉的關於 am 的信息。（這一點我覺得是比上一點更加 make sense 的）

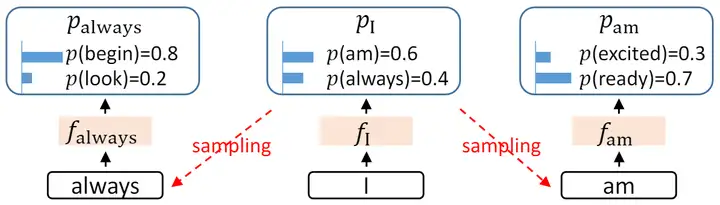
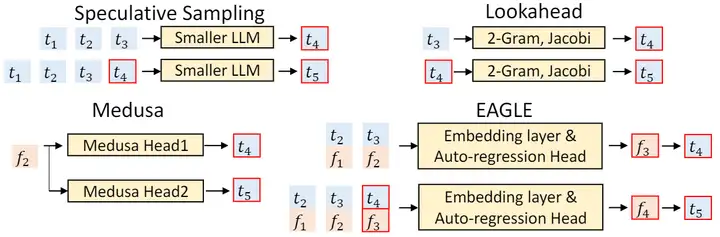
下圖對比了 EAGLE 和其它幾種 Speculative Decoding 方法。這裏， 𝑡𝑖 表示第 𝑖 次輸入的 token， 𝑓𝑖 表示 𝑡𝑖 經過 LLM 後在倒數第二層的輸出（即 LM Head 之前的輸出）。可以看到，EAGLE 創新性地選擇對 𝑓 做 Autoregressive Decoding。

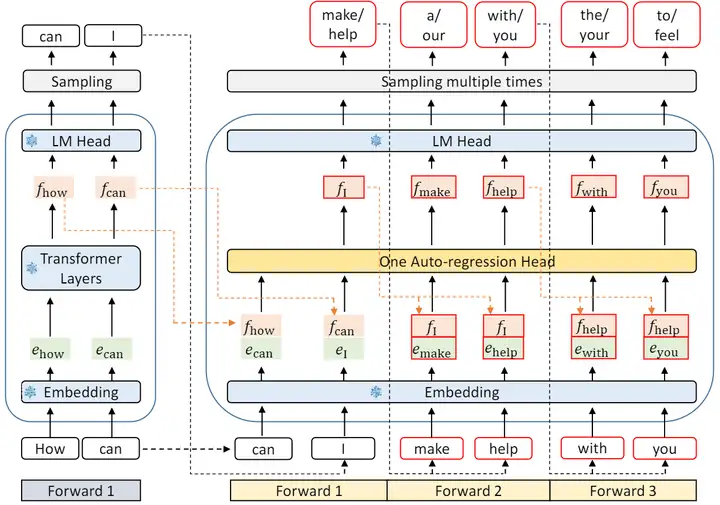
技術細節大致如下圖所示。作者將 embedding 和 特徵 𝑓 拼接在一起作爲 Draft Model 的輸入。這樣可以保留最終輸出 token 中遺失的其它信息。

這裏需要訓練的部分是自迴歸頭，由一個全連接層和一個 Decoder 層組成。全連接層的作用是將拼接後的向量降維至特徵維度。之後由 Decoder 層負責預測下一個特徵。這裏作者同樣採用了 Tree Attention 以達到一次驗證多個 sequence 的目的。

補充一點，這裏第一次前向傳播無法加速，因爲需要通過一次前向傳播才能得到後續 EAGLE 所需要的特徵。這裏也就能看出上一張圖裏作者畫自己的 EAGLE 的時候爲何要從 𝑡2 畫起。

之後便是這個自迴歸頭的訓練。作者用了兩個 loss。一個是特徵 𝑓 本身的重建 loss，另一個是自迴歸頭輸出的特徵與原模型特徵在經過 LM Head 之後的分類 loss。

理論上來說自迴歸頭需要使用原模型自迴歸生成的數據訓練。不過作者通過消融實驗證明了 EAGLE 對於訓練數據不敏感。因而作者使用了固定的數據集 ShareGPT，從而降低了訓練負擔。（這裏作者是直接把 ShareGPT 輸入了）

同時，作者指出，EAGLE 在訓練過程中自迴歸地生成特徵，這期間特徵的不準確會導致錯誤累積。因此作者在訓練數據上加了一個均勻分佈的隨機噪聲作爲數據增強。

效果極強，SOTA。

作者還提了個很有意思的點，就是 MoE 模型天生會和 Speculative Decoding 八字不合。因爲在 Vanilla Inference 階段，每個 token 只會需要兩個 experts 的權重。但 Speculative Decoding 的 verification 階段需要同時驗證多個 token，這就會削弱 MoE 的優勢，從而導致加速比的下降。在 Mixtral 8x7B 流行的背景下，這確實成了一個亟需解決的有趣問題。

Hierarchical Speculative Decoding

Cascade Speculative Drafting for Even Faster LLM Inference

[paper] [paper reading]

本文提出了 Vertical Cascade 和 Horizontal Cascade。Vertical Cascade 用 Speculative Decoding 來加速 Speculative Decoding。Horizontal Cascade 指的是在接受率較高的前幾個 token 用較大的 Draft Model，在接受率較小的靠後的 token 用較小的模型來“糊弄”（這個詞是我自己想到的，我看到文章的第一感覺就是這個詞，就是那種“反正也猜不準，隨便猜幾個得了”的感覺）。

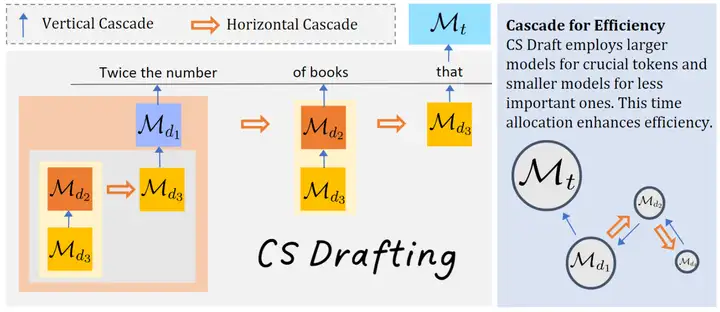
實驗部分用了 FLAN-T5-XXL (FLAN-T5-small, FLAN-T5-base) 和 LLaMA2 7B (LLaMA2 160M)。

實驗部分有這麼一段，感覺有些奇怪：Since we do not observe any significant difference between sampling with temperature 1 and greedy decoding in previous speculative decoding experiments (Leviathan et al., 2023), and to ensure our experiments are fully reproducible, we perform sampling at temperature0, i.e., using greedy decoding by default.

我感覺這可能還挺重要的，這麼做實驗的話那 Leviathan 的這篇最大的貢獻點 Speculative Sampling 就沒有存在的意義了。

TriForce: Lossless Acceleration of Long Sequence Generation with Hierarchical Speculative Decoding

[paper] [paper reading]

本文想解決的是 long-context generation 背景下的加速問題。在 long-context generation 設定下，除了模型本身的權重，模型推理的 KV cache 也會佔據大量的顯存，並在上下文足夠長的時候同樣成爲制約推理速度的關鍵因素。

因此，在 draft model 減小模型權重大小對於推理速度的制約之外，作者引入了一個只使用部分 KV cache 的 target model 來減小全量的 KV cache 對於推理速度的制約，從而構成了一種分層的 Speculative Decoding。

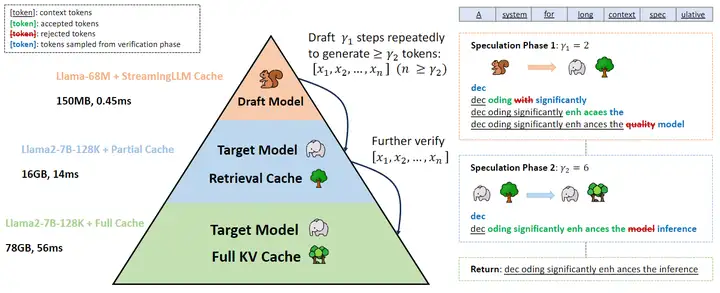
本文這個方法並不是全新的。事實上，《Cascade Speculative Drafting for Even Faster LLM Inference》這篇在之前就提出過類似的方法，但兩篇文章給人的觀感是截然不同。Cascade 這篇並沒有 long-context generation 這個設定，因此模型的分層設計就並不是很自然。但在本文中，兩次 Speculative Decoding 解決的問題是不同的，這裏的分層設計就非常的合理。（本文沒引用 Cascade，感覺……其實也可以不引，但還是引用一下比較好）

所以這裏的重點並不是包裝的藝術，而是尋找一個好問題的藝術。當你想賣出一瓶洗髮水又恰好碰見一位僧人的時候，重點並不是如何兜售，而是果斷換一個推銷對象。

Draft Model 與 Target Model 的對齊

DistillSpec: Improving Speculative Decoding via Knowledge Distillation

[paper] [paper reading]

非常直觀的想法：知識蒸餾（KD）用於 Speculative Decoding 可以提高 acceptance rate，從而提高加速比

既然用到了語言模型的 KD，那麼我們必須要問兩個問題：用什麼蒸餾方法？用什麼數據？

對於第一個問題，作者用實驗說明了最優的蒸餾方法很大程度上取決於任務和 Decoding Strategy。

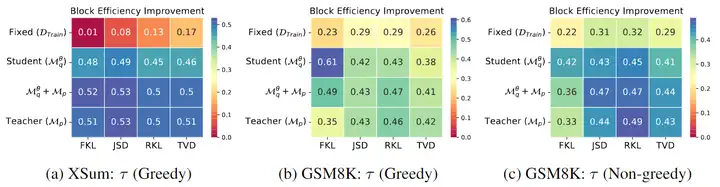
對於第二個問題，作者證明了：如果在 draft model 生成的 𝑦 上，target model 和 draft model 的預測機率分佈差距越小，那麼 acceptance rate 的下界越高，這爲使用 draft model 生成的 𝑦 進行 KD 提供了理論保證。之後作者用實驗證明，模型生成的數據上蒸餾的效果要優於固定的數據集，且使用 target model 生成的 𝑦 和使用 draft model 生成的 𝑦 蒸餾效果差不多（上圖第一行是固定的數據集，顯著劣於後三行模型生成的數據）。由於 draft model 更小，生成數據的成本更低，作者建議選用 draft model 生成的 𝑦 進行蒸餾。

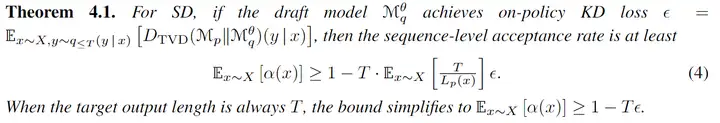
Online Speculative Decoding

[paper] [paper reading]

本文把在線知識蒸餾融入了 Speculative Decoding。

在 Speculative Decoding 階段，會記錄下所有 Draft Model 的錯誤猜測，並將對應的正確猜測放入 Replay Buffer。每隔一段時間，用 Replay Buffer 內的數據訓練 Draft Model，使得 Draft Model 在用戶當前的輸入分佈上與原模型更好的對齊。之後清空 Replay Buffer 並繼續正常的 Speculative Decoding。

蒸餾過程中也用到了一些之前研究 LLM 蒸餾的文章提到的 tricks，這裏不贅述了。

實驗部分，用了 Vicuna-7B（LLaMA-160M）和 Flan-T5-XL 3B（T5-small 80M）。

其它的 Draft Model 創新

SpecTr: Fast Speculative Decoding via Optimal Transport

寫的簡短一些。一是因爲這個方法明顯比不過 Tree Verification，已經沒什麼人用了。二是因爲 optimal transport 我並不是很懂，看了文章現學的，學了也沒太看懂理論部分在幹啥。

本文想解決的問題是多個 draft sequence 如何選擇的問題，大致如下圖（按下圖的 caption 描述就是數個數）：

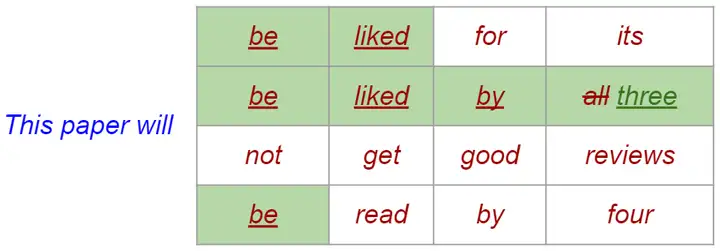
本文用了大量 optimal transport 的理論分析，證明了 Speculative Sampling 在只猜測下一個 token 的時候是最優的，並指出最優的 draft 選擇可以使用線性規劃得到。

REST: Retrieval-Based Speculative Decoding

[paper] [paper reading]

本文沒有 Draft Model，而是使用現成的數據庫替代 Draft Model 的輸出。具體分爲三步：

1. 在文檔中尋找最長匹配後綴。
2. 將檢索到的這些條目構建爲字典樹。用條目出現頻率設置爲字典樹中結點的權重。
3. 使用類似於 SpecInfer 和 Medusa 的方法構建 Tree-based Attention，爾後進行 verify。

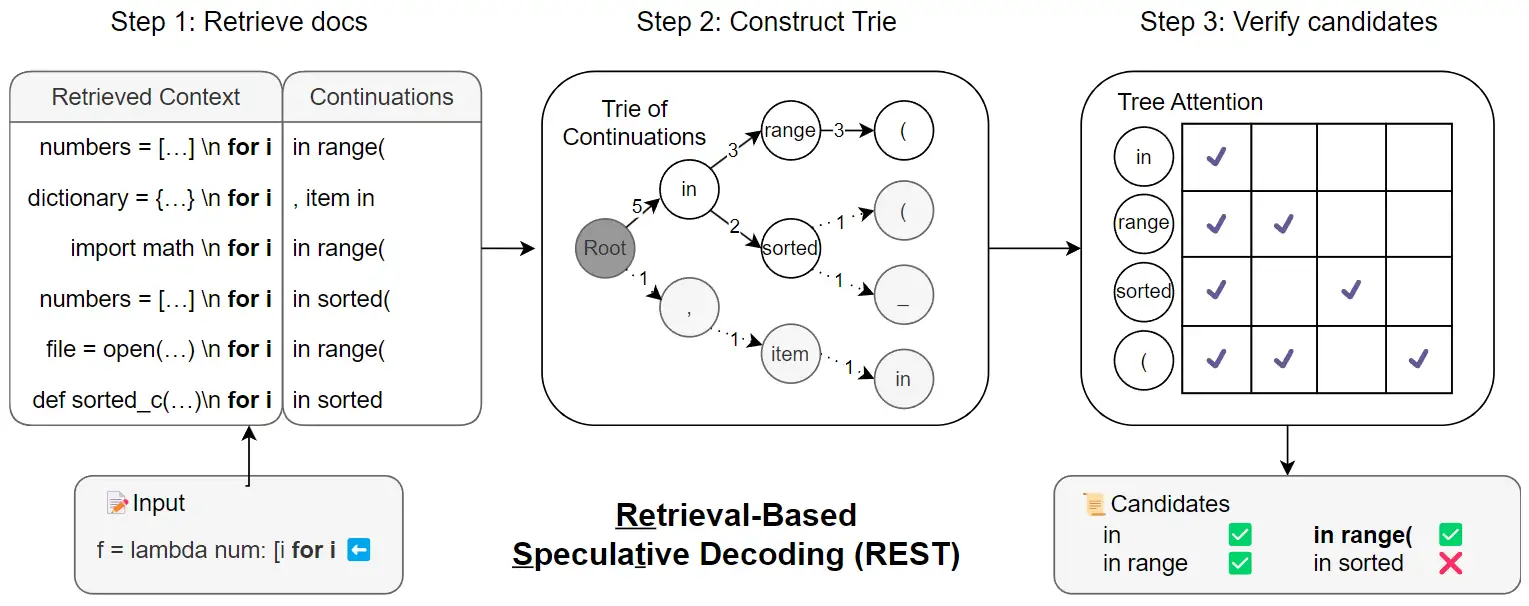
實驗部分，HumanEval 數據集上用的是 CodeLlama 7B、13B，用來檢索的數據集是 TheStack；MT-Bench 數據集上用的是 Vicuna 7B、13B，用來檢索的數據集是 UltraChat。

Predictive Pipelined Decoding: A Compute-Latency Trade-off for Exact LLM Decoding

[paper] [paper reading]

本文的想法是把 Early-Exiting 與 Speculative Decoding 相結合，使用模型中間層的輸出作爲預測。這個結構就很有計算機多級流水的味道。

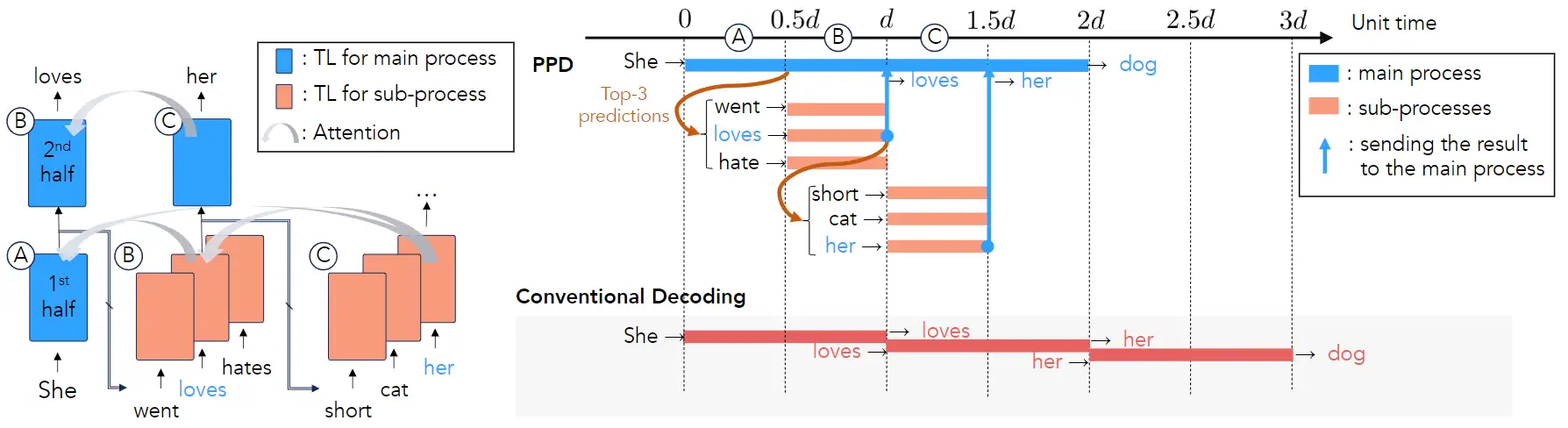
作者並沒有完整地實現整個算法，畢竟按這個結構，即使是選取 top-3，也需要四倍顯存，這明顯不太實用。當然，如果把後續 SpecInfer 和 Medusa 裏的 tree-based attention 用進來的的話，那就是永遠是兩倍顯存。但即使是這樣也並不很省顯存，而且加速比可能並不會很突出。

Draft & Verify: Lossless Large Language Model Acceleration via Self-Speculative Decoding

[paper] [paper reading]

本文將 skip 部分層原模型的原模型作爲 Draft Model。如下圖所示，在 Drafting 階段會跳過一些層，而在 Verification 階段會通過所有層。那麼下一步要解決的問題就是究竟需要跳過哪些層。

本文采用了一種貝葉斯優化的方法，使用 Gaussian Process 來優化層掩碼，在優化完成後固定這一掩碼，並直接用在了後續的 Self-Speculative Decoding 中。

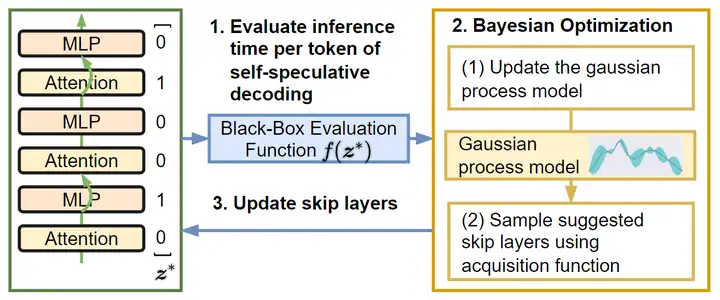
由於在本文的設定下模型無法同時扮演 Draft Model 和原模型的角色，作者專門討論了何時停止 Draft 轉而進行 Verification 的問題。本文的解決方案是設置了一個根據 Accept Rate 動態變化的自適應閾值，當下一個 token 的預測機率小於閾值的時候停止 Drafting。

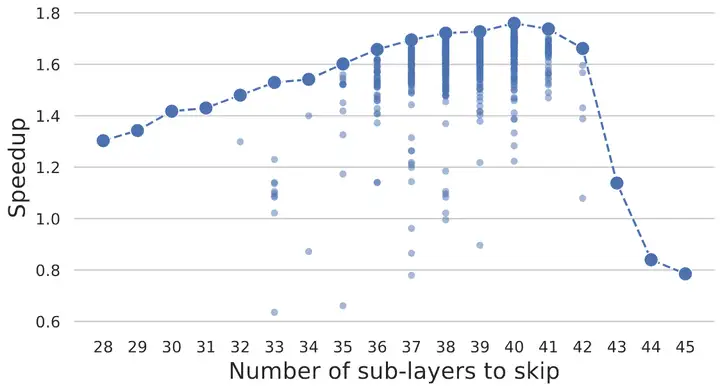
實驗部分用了 LLaMA-2-13B, LLaMA-2-13B-Chat, CodeLLaMA-13B 和 LLaMA-2-70B。貼一張關於 skip 層數的圖。可以看到，在 skip 一半的層的時候有一個加速比的高峯，skip 的層數超過一半之後，Drafting 給出的猜測準確率就會大幅下降，導致雖然 Drafting 速度變快但整體加速比急劇下降，甚至低於1。

Speculative Decoding with Big Little Decoder

[paper] [paper reading]

本文把是否需要大模型進行確認的權力交給了小模型，稱之爲 Fallback。Fallback 之後，對於兩次 Fallback 之間小模型生成的 token，引入 Rollback 確保其性能。

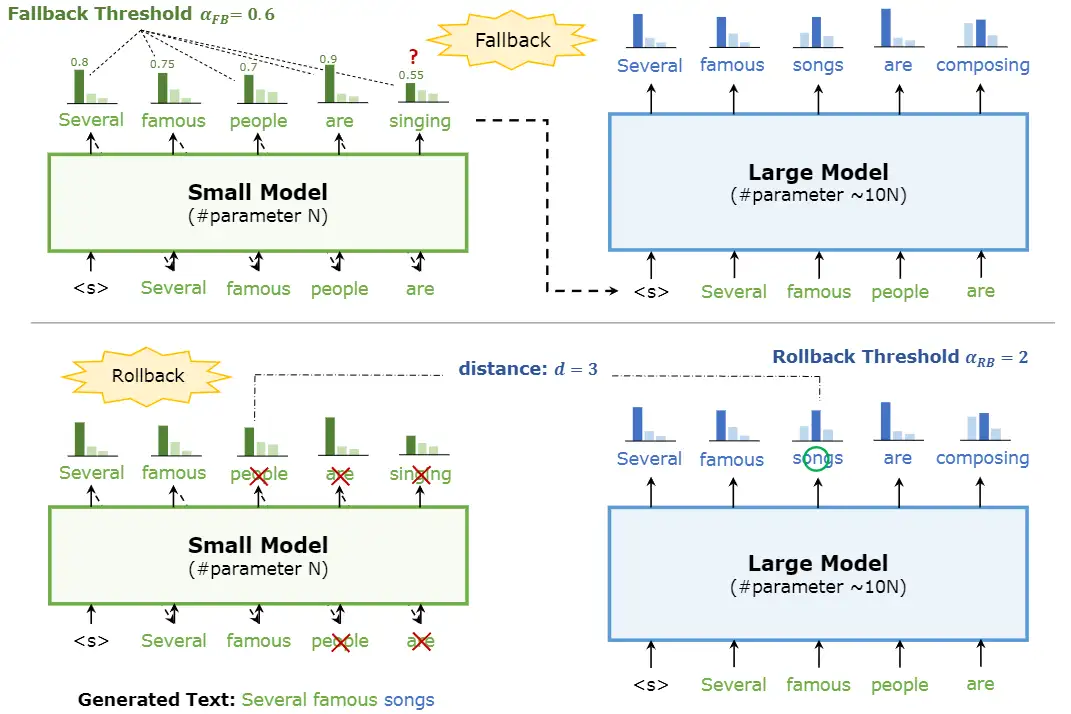
具體來說，一旦小模型在當前 token 輸出機率的最大值低於設定的閾值 𝛼𝐹𝐵，就進行 Fallback，開始引入大模型進行 verify。在 verify 過程中，計算每個 token 上大小模型輸出機率之間的距離 𝑑，一旦 𝑑 大於設定的閾值 𝛼𝑅𝐵，就將此 token 改爲大模型的輸出，並讓小模型在後續從這個 token 開始生成。

此方法無法確保輸出與原模型完全一致。實驗的模型比較小，未超過 1B。

PaSS: Parallel Speculative Sampling

[paper] [paper reading]

本文在現有的輸入之後加上了一些 lookahead tokens，然後用這些 tokens 的輸出當作猜測，並用 Speculative Decoding 進行驗證。這些 lookahead tokens 的 embedding 是可學習的。

實驗用的是 7B 的 LLaMA。

Generation Meets Verification: Accelerating Large Language Model Inference with Smart Parallel Auto-Correct Decoding

[paper] [paper reading]

本文兩張圖畫得還是很明白的，可以算是一種 self speculative decoding。第一張圖右側畫的是大體框架，具體的生成與驗證的細節在第二張圖上。

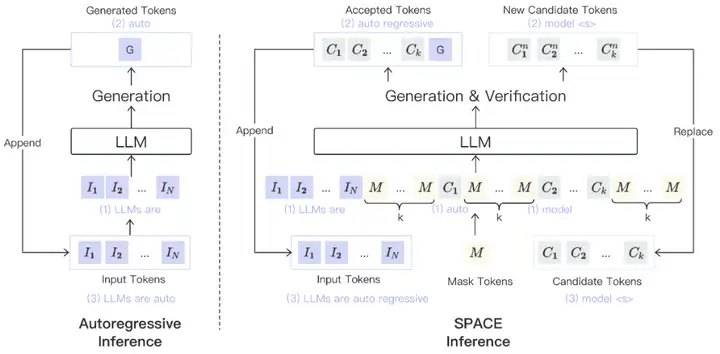
具體來說，就是所有的 𝑘 個 candidate token 在 verification 的時候並不是緊鄰着的，兩兩中間穿插了 𝑘 個 mask token，verification 進行到第一個被 reject 的 token 時，這個 token 之後所生成的 𝑘 個 token 作爲下一次 verification 的 candidate token。

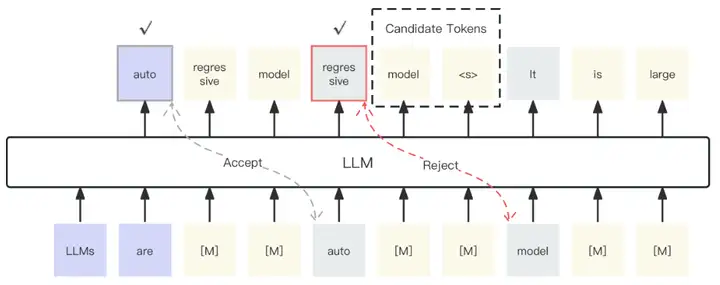
本文的方法很奢侈，除了被 reject 的那一個 token 之後的 𝑘 個 token，其它的 mask token 是註定是會被浪費的，這在帶寬受限的非計算卡上尤爲致命。而 Medusa 的處理方法和此方法很像，卻沒有這個問題。同時，Medusa 使用了 Tree Verification 而此方法很難使用，因此此方法在性能上能否比過 Medusa 也是要打問號的。

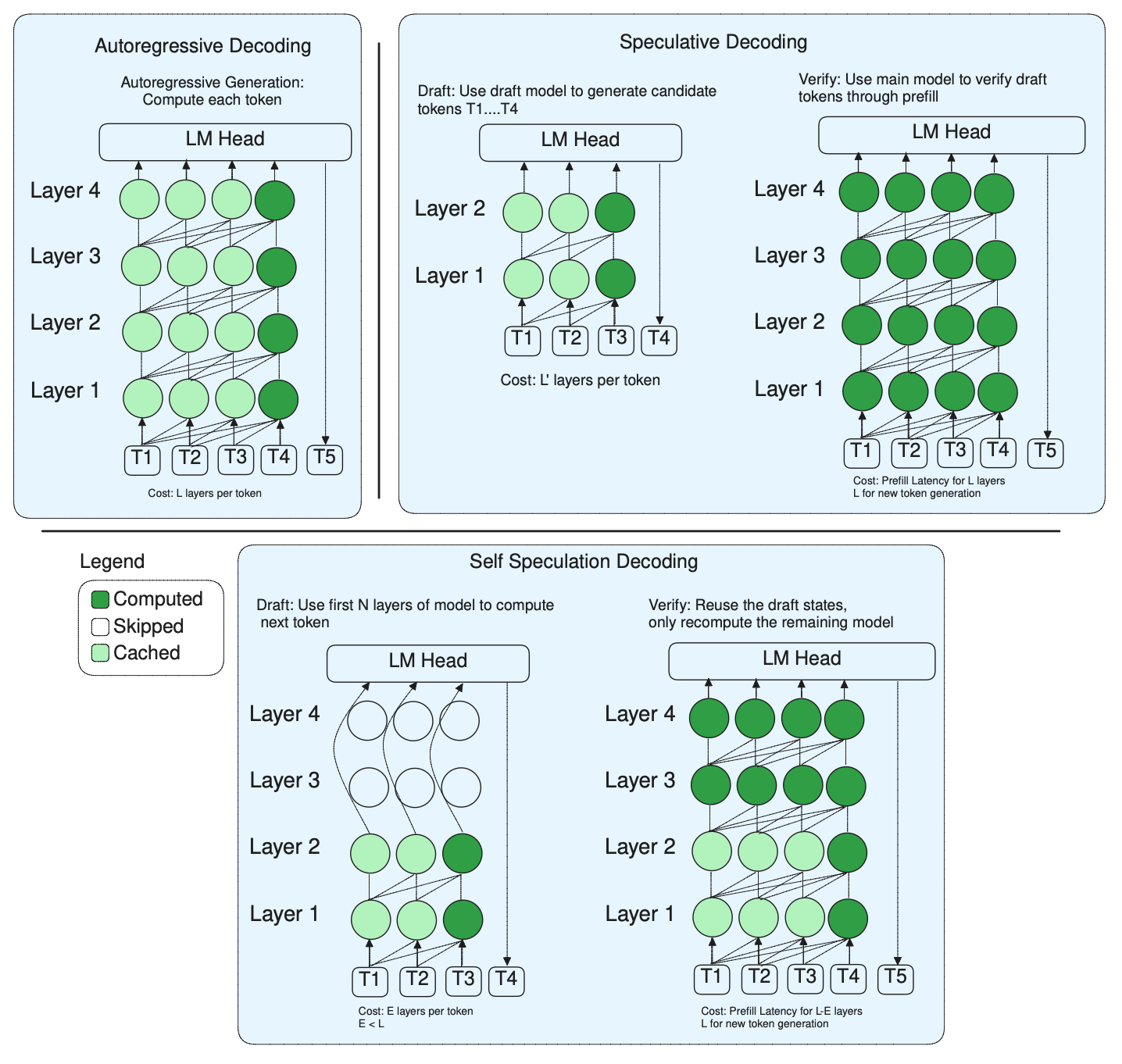
LayerSkip: Enabling Early Exit Inference and Self-Speculative Decoding

[paper]

1. Self-drafting
2. parallel verification

Lookahead Key Technology

$\boldsymbol{x}$ : prompt, $\boldsymbol{y}=\left[y_1, y_2, \ldots, y_m\right]: m$ tokens to decode, $p(\boldsymbol{y} \mid \boldsymbol{x}):$ LLM distribution

Define: $f\left(y_i, \boldsymbol{y}{1: i-1}, \boldsymbol{x}\right)=y_i-\operatorname{arg max} p\left(y_i \mid \boldsymbol{y}{1: i-1}, \boldsymbol{x}\right)$ \(\left\{\begin{array} { l } { y _ { 1 } = \operatorname { arg max } p ( y _ { 1 } | \boldsymbol { x } ) } \\ { y _ { 2 } = \operatorname { arg max } p ( y _ { 2 } | y _ { 1 } , \boldsymbol { x } ) } \\ { \vdots } \\ { y _ { m } = \operatorname { arg max } p ( y _ { m } | \boldsymbol { y } _ { 1 : m - 1 } , \boldsymbol { x } ) } \end{array} \quad \equiv \quad \left\{\begin{array}{l} f\left(y_1, \boldsymbol{x}\right)=0 \\ f\left(y_2, y_1, \boldsymbol{x}\right)=0 \\ \vdots \\ f\left(y_m, \boldsymbol{y}_{1: m-1}, \boldsymbol{x}\right)=0 \end{array}\right.\right. \\ \text{Autoregressive decoding}\quad \text{Nonlinear system with m variables and m equations}\) $m$ 代表 $m$-gram? No, $m$ 是 token number.

An alternative approach based on Jacobi iteration can solve all $[y_1,y_2,…,y_m]$ of this nonlinear system in parallel as follows:

• Start with an initial guess for all variables $y = [y_1,y_2,…,y_m]$.
• Calculate new y′ values for each equation with the previous y.
• Update y to the newly calculated y′.
• Repeat this process until a certain stopping condition is achieved (e.g., y=y′).

We illustrate this parallel decoding process (also referred to as Jacobi decoding) in Figure 3. Jacobi decoding can guarantee solving all $m$ variables in at most $m$ steps (i.e., the same number of steps as autoregressive decoding) because each step guarantees at least the very first token is correctly decoded. Sometimes, multiple tokens might converge in a single iteration, potentially reducing the overall number of decoding steps.

Jacob Decode

Jacob decode 原理如下：

• 左圖是傳統的 autoregressive decode. 需要 $m$ 個 step 才能得到 $m$ tokens.
• 右圖是 Jocob parallel decode. 可以想像 parallel decoding 的 input 是 guess tokens, 經過 parallel decoding 產生 output tokens. Output tokens 經過 decoder 做 parallel verification. 經過 $k$ 次 iteration 得到 $m$ tokens. 如果算法夠聰明，讓 $k < m$, 基本就賺到。Speed up = $m/k$.

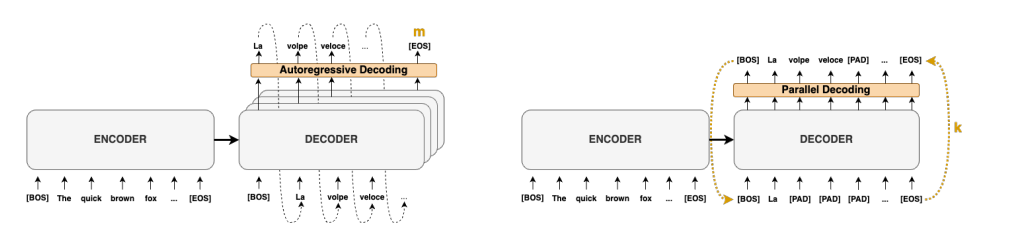
• Jacob decode 就是這個”聰明的算法“。
• Autoregressive decoding 的算法就是下表左。

• Jocob 算法就是利用上表右，得到的下表：
  • Stop criterion: 就是 input m tokens 等於 output m tokens => fully verified. 如果 k 次達成而且 $k < m$ 就有 speed up.

如何得到 guess tokens? Jacob decode. 問題：如何得到 $p_{\theta}()$ conditional probability.

Transformer model 最大的好處！！

• Distribution probability 直接就在 softmax 之後！！

Parallel verified: 和 speculative decode 一樣

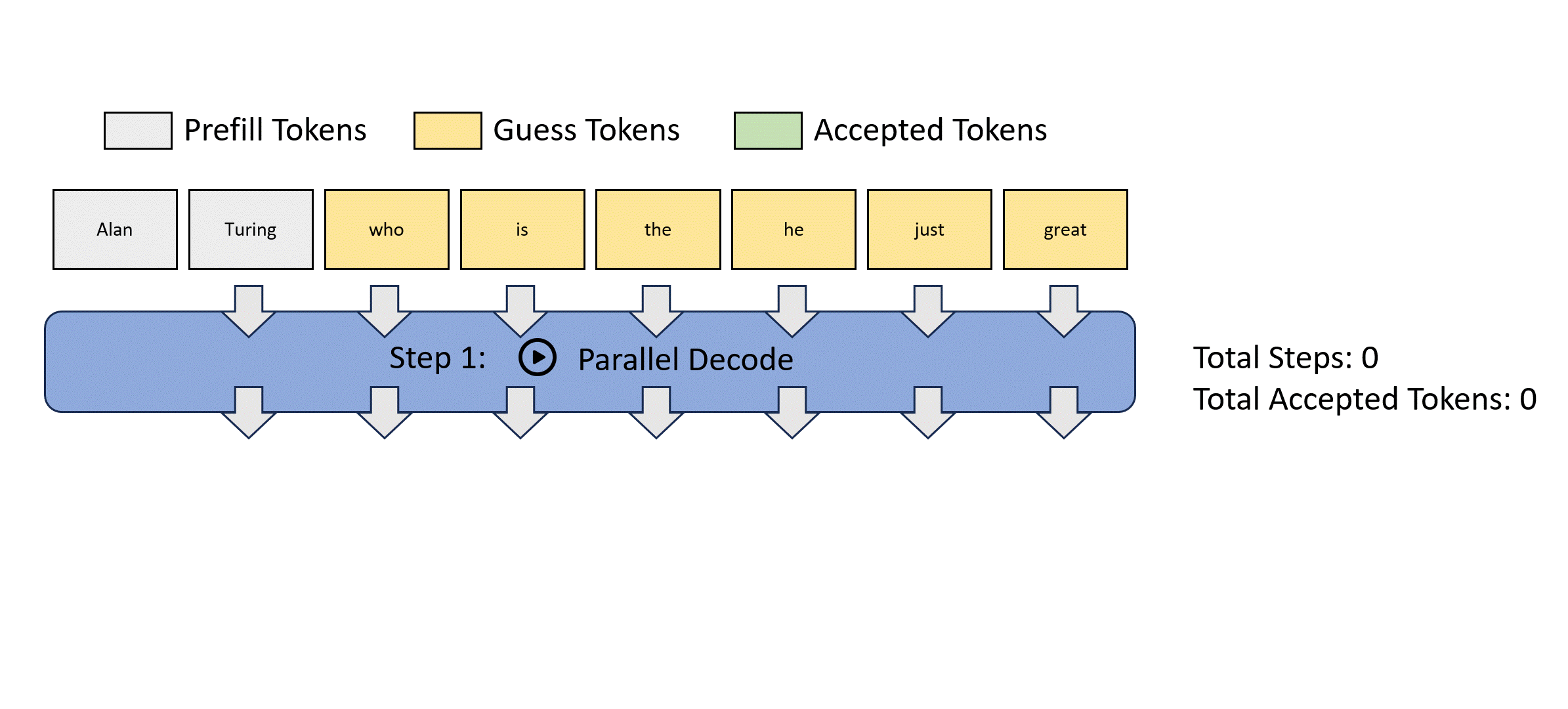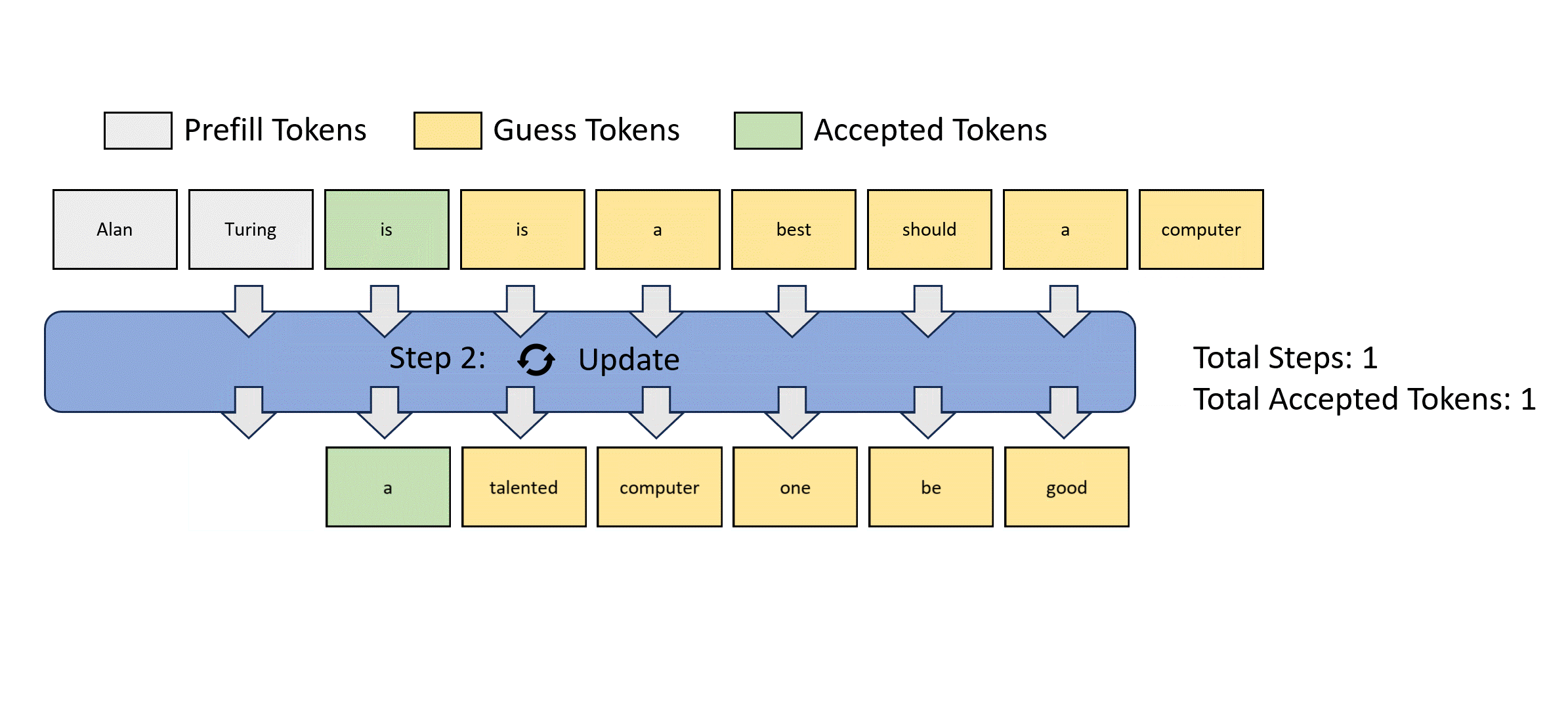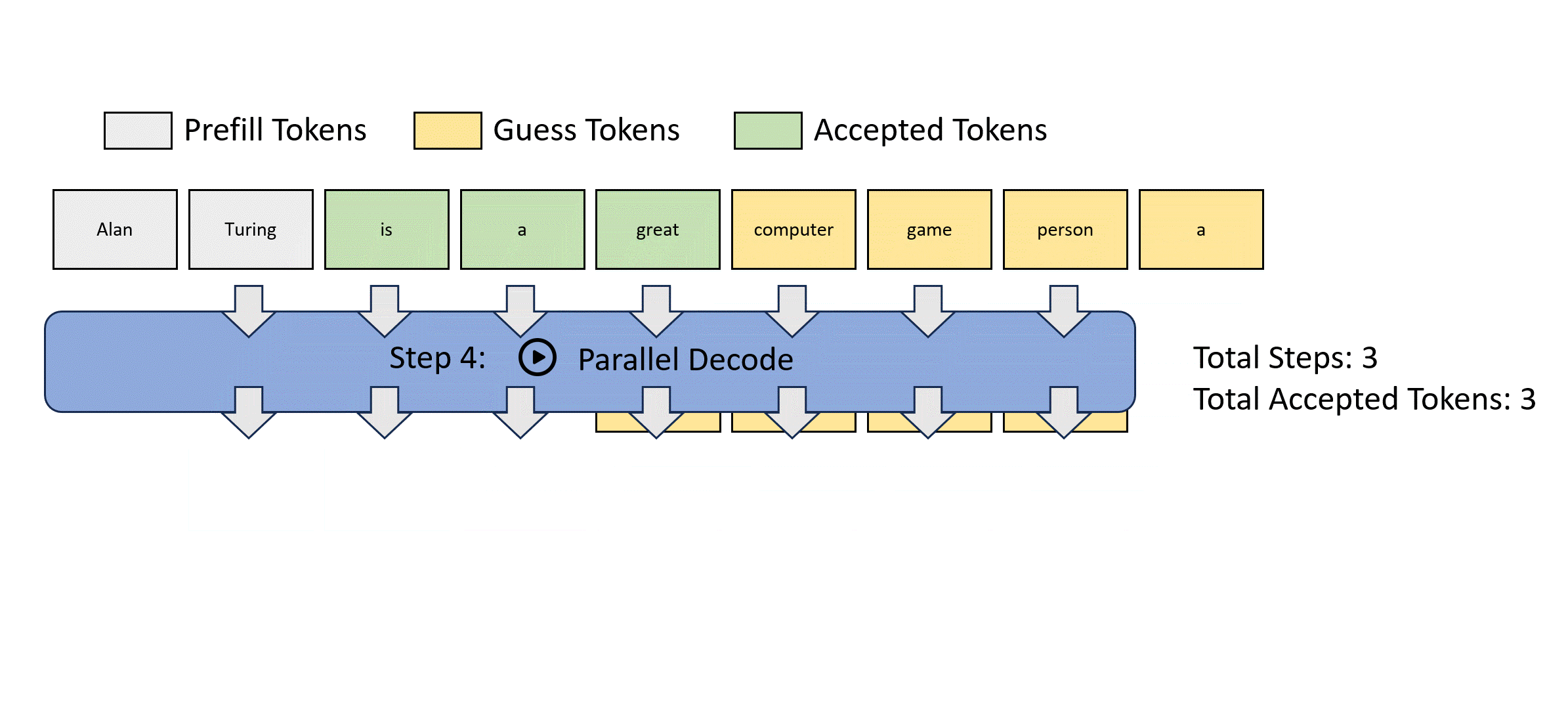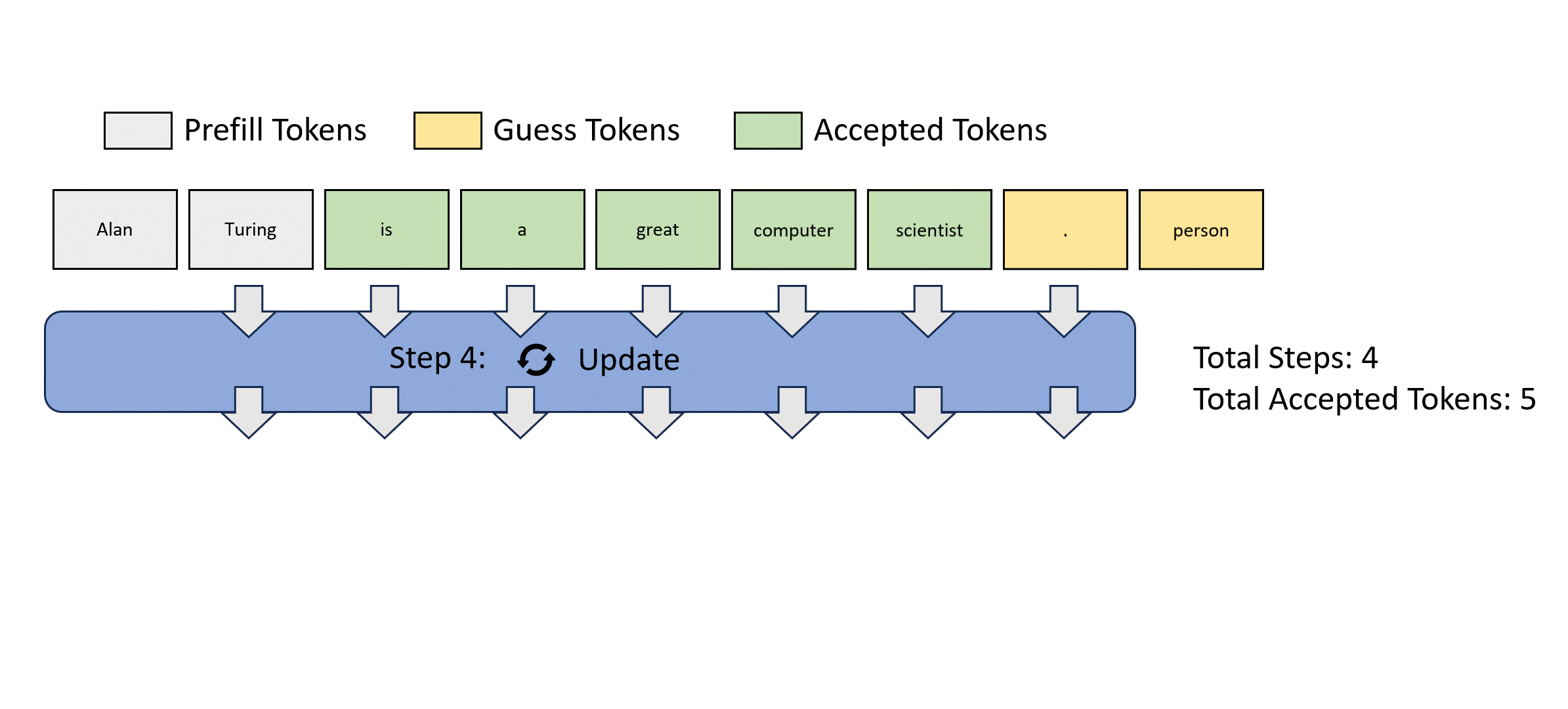
N-gram

• 2-gram to N-gram 可以幫忙 Jacob decode 更有效率？

Lookahead = Jacob + N-gram

Lookahead Branch + Verification Branch

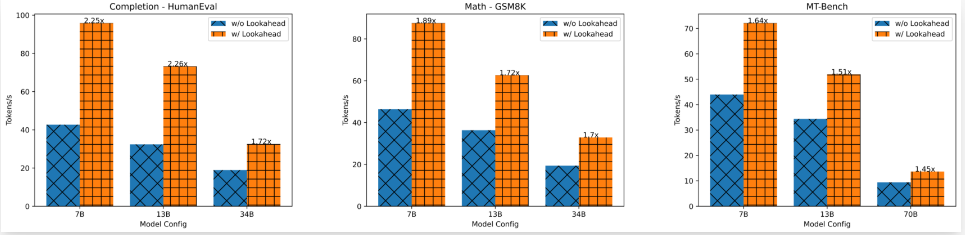
Speed Up

• 小 model 似乎效果最好。這和 speculative decode 剛好相反？

Appendix

1. 对于 prompt $x_1, \ldots, x_n$ ，先用 draft 模型 (小模型) 去 autoregressive 地生成 $\tilde{x}{n+1}, \ldots, \tilde{x}{n+K}$ ，顺便得到 $\mathbf{P}{\text {draft }}\left(X \mid x_1, \ldots, x_n, \tilde{x}{n+1}, \ldots, \tilde{x}_{n+i-1}\right) ，(1 \leq i \leq K)$ ；
2. 然后把 $x_1, \ldots, x_n, \tilde{x}{n+1}, \ldots \tilde{x}{n+K}$ 作为 target model (大模型) 的输入，一次性得到 $\mathbf{P}{\text {target }}\left(X \mid x_1, \ldots, x_n, \tilde{x}{n+1}, \ldots, \tilde{x}_{n+i-1}\right) ，(1 \leq i \leq K)$ ；
3. for $\mathrm{t}$ in range( $\mathrm{k}+1)$
   • 随机生成 $r \sim U[0,1]$ ，如果 $r<\min \left(1, \mathbf{P}{\text {target }}\left(\tilde{x}{n+t} \mid x_1, \ldots \tilde{x}{n+t-1}\right) / \mathbf{P}{\mathrm{draft}}\left(\tilde{x}{n+t} \mid x_1, \ldots \tilde{x}{n+t-1}\right)\right)$ ，那么 $n+t$ 位置就用 $\tilde{x}_{n+t}$ ，
   • 不然，认为 draft 模型和 target 模型偏差有些大了，就退出循环，并用之前得到的结果来随机出 $x_{n+t}$ : \(x_{n+t} \sim\left(\mathbf{P}_{\text {target }}\left(X \mid x_1, \ldots, \tilde{x}_{n+t-1}\right)-\mathbf{P}_{\text {draft }}\left(X \mid x_1, \ldots, \tilde{x}_{n+t-1}\right)\right)_{+}\)

这个方法的一个重点在于，他是精确解，不是近似解。简单推一下公式，有: \(\begin{aligned} \mathbf{P}\left(\text { target 选 } x_i\right)= & \sum_j \mathbf{P}\left(\text { target 选 } x_i \mid \text { draft 选 } x_j\right) \mathbf{P}\left(\text { draft 选 } x_j\right) \\ = & \mathbf{P}\left(\text { target 选 } x_i \mid \text { draft 选 } x_i\right) \mathbf{P}\left(\text { draft 选 } x_i\right) \\ & +\sum_{j \neq i} \mathbf{P}\left(\text { target 选 } x_i \mid \text { draft 选 } x_j\right) \mathbf{P}\left(\text { draft 选 } x_j\right) \\ = & \min \left(1, \frac{\mathbf{P}_{\mathrm{T}}\left(x_i\right)}{\mathbf{P}_{\mathrm{D}}\left(x_i\right)}\right) \mathbf{P}_{\mathrm{D}}\left(x_i\right)+ \\ & \sum_{j\ne i}\left(1-\min \left(1, \frac{\mathbf{P}_{\mathrm{T}}\left(x_j\right)}{\mathbf{P}_{\mathrm{D}}\left(x_j\right)}\right)\right) \frac{\max \left(0, \mathbf{P}_{\mathrm{T}}\left(x_i\right)-\mathbf{P}_{\mathrm{D}}\left(x_i\right)\right)}{\sum_k \max \left(0, \mathbf{P}_{\mathrm{T}}\left(x_k\right)-\mathbf{P}_{\mathrm{D}}\left(x_k\right)\right)} \mathbf{P}_{\mathrm{D}}(x_j) \\ = & \min \left(\mathbf{P}_{\mathrm{D}}\left(x_i\right), \mathbf{P}_{\mathrm{T}}\left(x_i\right)\right)+ \\ & \max \left(0, \mathbf{P}_{\mathrm{T}}\left(x_i\right)-\mathbf{P}_{\mathrm{D}}\left(x_i\right)\right) \frac{\sum_{j\ne i}\left(\mathbf{P}_{\mathrm{D}}\left(x_j\right)-\min \left(\mathbf{P}_{\mathrm{D}}\left(x_j\right), \mathbf{P}_{\mathrm{T}}\left(x_j\right)\right)\right.}{\sum_k \max \left(0, \mathbf{P}_{\mathrm{T}}\left(x_k\right)-\mathbf{P}_{\mathrm{D}}\left(x_k\right)\right)} \\ = & \min \left(\mathbf{P}_{\mathrm{D}}\left(x_i\right), \mathbf{P}_{\mathrm{T}}\left(x_i\right)\right)+ \\ & \max \left(0, \mathbf{P}_{\mathrm{T}}\left(x_i\right)-\mathbf{P}_{\mathrm{D}}\left(x_i\right)\right) \frac{\left.\sum_{j\ne i} \max \left(0, \mathbf{P}_{\mathrm{D}}\left(x_j\right)-\mathbf{P}_{\mathrm{T}}\left(x_j\right)\right)\right)}{\sum_k \max \left(0, \mathbf{P}_{\mathrm{T}}\left(x_k\right)-\mathbf{P}_{\mathrm{D}}\left(x_k\right)\right)} \\ = & \min \left(\mathbf{P}_{\mathrm{D}}\left(x_i\right), \mathbf{P}_{\mathrm{T}}\left(x_i\right)\right)+ \\ & \max \left(0, \mathbf{P}_{\mathrm{T}}\left(x_i\right)-\mathbf{P}_{\mathrm{D}}\left(x_i\right)\right) \frac{\left.\sum_{j} \max \left(0, \mathbf{P}_{\mathrm{D}}\left(x_j\right)-\mathbf{P}_{\mathrm{T}}\left(x_j\right)\right)\right)}{\sum_k \max \left(0, \mathbf{P}_{\mathrm{T}}\left(x_k\right)-\mathbf{P}_{\mathrm{D}}\left(x_k\right)\right)} \\ = & \min \left(\mathbf{P}_{\mathrm{D}}\left(x_i\right), \mathbf{P}_{\mathrm{T}}\left(x_i\right)\right)+\max \left(0, \mathbf{P}_{\mathrm{T}}\left(x_i\right)-\mathbf{P}_{\mathrm{D}}\left(x_i\right)\right) \\ = & \mathbf{P}_{\mathrm{T}}\left(x_i\right)=\mathbf{P}_{\mathrm{target}}\left(x_i \mid x_1, \ldots x_{i-1}\right) \end{aligned}\) 这里的倒数第四行到倒數第三行的推導利用 $\max \left(0, \mathbf{P}{\mathrm{T}}\left(x_i\right)-\mathbf{P}{\mathrm{D}}\left(x_i\right)\right)\max \left(0, \mathbf{P}{\mathrm{D}}\left(x_i\right)-\mathbf{P}{\mathrm{T}}\left(x_i\right)\right)=0$

这里的倒数第三行到倒数第二行的推导需要考虑到，因为 $\sum_i \mathbf{P}{\mathrm{D}}\left(x_i\right)=\sum_i \mathbf{P}{\mathrm{T}}\left(x_i\right)=1$ ，若令 $\mathcal{I}=\left{i \mid \mathbf{P}{\mathrm{D}}\left(x_i\right) \leq \mathbf{P}{\mathrm{T}}\left(x_i\right)\right}$ ，那么会有: \(\sum_{i \in \mathcal{I}} \mathbf{P}_{\mathrm{T}}\left(x_i\right)-\mathbf{P}_{\mathrm{D}}\left(x_i\right)=\sum_{i \notin \mathcal{I}} \mathbf{P}_{\mathrm{D}}\left(x_i\right)-\mathbf{P}_{\mathrm{T}}\left(x_i\right)\)

也就是: \(\sum_i \max \left(0, \mathbf{P}_{\mathrm{T}}\left(x_i\right)-\mathbf{P}_{\mathrm{D}}\left(x_i\right)\right)=\sum_i \max \left(0, \mathbf{P}_{\mathrm{D}}\left(x_i\right)-\mathbf{P}_{\mathrm{T}}\left(x_i\right)\right)\)

Reference

大語言模型量化方法對比：GPTQ、GGUF、AWQ - 知乎 (zhihu.com)

QLoRA——技術方案總結篇 - 知乎 (zhihu.com)

[@guodongLLMTokenizer2023]