LLM - Medusa on GPU with Limited Memory

Posted on | In

LLM 最大的問題是 memory footprint and memory bandwidth. 有多種方式，但是萬變不離其宗都是把 autoregressive 的 sequential decode 變成 parallel decode (verfication). 目前常見有三種：

  • Speculative decode: 利用小 (draft model) 和大 (native model) 模型達成加速。
  • Medusa decode: 利用 multi-heads 的 information 預測達成加速。
  • Lookahead decode: 利用數學的解聯立方程式的迭代法 (Jacob or GS-Jacob) 達成加速。
  • Encode (prompt, parallel) + decode (generative): 利用 prompt parallel mode 的 hint 給 decode.

本文試著在 GTX1080 with 8GB DRAM 的 GPU 跑 Llama2 model.

Medusa Model

Medusa 提供 Llama2-7B/13B/70B 的 model. 主要是 Vicuna fine-tune Llama using ShareGPT dialog data. 之後 Meta 才又 release Llama2 native model 和 Llama2-chat fine tune model.

meta-llama/Llama-2-70b-chat-hf · Hugging Face

所以有兩個 models: (1) Original model: Vicuna; (2) Medusa heads model.

image-20231210192433033

因爲 GTX1080 GPU 只有 8GB DRAM, 此處只考慮 7B model.

Step 1: install medusa

1
llama2>  pip install medusa-llm

Step 2: Copy Medusa to local.

1
llama2> git clone https://github.com/FasterDecoding/Medusa.git

Step 3：下載 (1) Vicuna model; 以及 (2) Medusa-Vicuna model

  • Download Hugging Face Vicuna-7b-v1.3 model (13.5GB): https://huggingface.co/lmsys/vicuna-7b-v1.3/tree/main
  • Download medusa-vicuna-7b-v1.3 model (1.48GB): https://huggingface.co/FasterDecoding/medusa-vicuna-7b-v1.3/tree/main

我們大約可以估計：

  • Original Vicuna-7B model: 7B 參數, 2-byte (FP16 or BF16?) per parameter, memory footprint: 13.5GB
  • Medusa head model: 0.7B? 參數, 2-byte per parameter, memory footprint: 1.5GB, 大約 10% overhead.

如果執行 Medusa, 一共有

  • 7.7B 參數，大約 15GB memory footprint, 再加上 KV cache 和其他 memory, 很容易就大於 > 16GB.
  • 所以只能用 4-bit weight, 才有機會在 GTX-1080. 8-bit 基本也沒有機會。

執行 Medusa Model

記得有兩個 models, 分別稱爲

  • base-model: vicuna-7b-v1.3
  • model: medusa-vicuna-7b-v1.3

我們只考慮 inference

Inference

1
python -m medusa.inference.cli --model /mnt/c/Users/allen/llama/medusa-vicuna-7b-v1.3 --load-in-4bit
  • cli 是 command line interface
  • –model 就是 medusa model
  • –base-model 是 original model
  • –load-in-4bit (or –load-in-8bit) 是改用 4bit (or 8bit) 參數以節省 memory

Medusa 原理

Coffee shop ? A ‘SS’IST’ANT’ : Once upon a time , in a small mountain ‘nest’led’ in shop ? \n story S \n I Once upon a time , in a small village village led between the …

達到模型輸出的平衡 (Markov Equilibrium)

當我們討論美杜莎驗證時,一個核心概念是模型輸出的平衡狀態。

想像一下由模型生成的序列。這個序列由兩部分組成:

  • Prompt: 這是給予模型的初始輸入。

  • Predictions (generation): 這些是模型對 prompt 的響應而生成的 tokens。

將這些段落合併便得到了整個序列 concat([prompt, preds])。為了清晰,我們用 n 表示 prompt 的長度,用 k 表示 preds 的長度。

一個顯著的特點是,如果將這個合併後的序列再輸入模型,它會重現相同的預測。這意味著合併序列中的 preds 部分由於模型的生成能力已達到平衡。

為了更好地理解,這裡是一個視覺化的表示:

Input(prompt) ... 'shop' '?' 'A' 'SS' 'IST' 'ANT' ':'
模型 output ... '?'
&#9989		 '\\n'
&#x274C		 'story'
&#x274C		 'S'
&#x274C		 '\\n'
&#x274C		 'I'
&#x274C		 ...

續表:

Input(preds) ... 'Once' 'upon' 'a' 'time' ',' 'in' 'a' 'small' 'village' 'nest' 'led' 'in'
模型output 'Once'
&#9989		 'upon'
&#9989		 'a'
&#9989		 'time'
&#9989		 ','
&#9989		 'in'
&#9989		 'a'
&#9989		 'small'
&#9989		 'village'
&#9989		 'nest'
&#9989		 'led'
&#9989		 'in'
&#9989		 'the'

在這個示例中,頂行顯示了輸入 concat([prompt, preds])。第二行代表模型的輸出標記 - 本質上是移位的輸入標記,最終結果是下一個標記。雖然提示偏離是因為它不是模型生成的直接結果,但從 [n - 1: n - 1 + k] 範圍內的輸出標記與 [n: n + k] 範圍內的輸入標記完全對齊。

通過輕微更改干擾平衡狀態

為了強調平衡狀態的敏感性,我們來看另一個示例。

從我們之前的說明中,“Once upon a time, in a small village nestled in”這個序列已達到平衡狀態,將此序列反饋到模型中會產生相同的預測。

但是,如果我們對這種平衡狀態引入輕微的變化會發生什麼?

為了這個示範的目的,我們將 “village” 一詞替換為 “mountain”。從語法和語義的角度來看,這兩個詞在故事中都很合適。然而,正如我們將看到的,在 “mountain” 一詞之後,模型隨後的輸出與我們原來的序列有很大的偏差。

這是視覺化表示:

Input ... ':' 'Once' 'upon' 'a' 'time' ',' 'in' 'a' 'small' 'mountain'&#128221 'nest' 'led' 'in'
模型Output ... 'Once'
&#9989		 'upon'
&#9989		 'a'
&#9989		 'time'
&#9989		 ','
&#9989		 'in'
&#9989		 'a'
&#9989		 'small'
&#9989		 'village'
&#9989		 'village'
&#x274C		 'led'
&#9989		 'between'
&#x274C		 'the'
&#10067

Medusa vs. Speculative Decode

現在,我們可以從另一個角度重新思考這個問題。你被給予之前的 prompt,一個算命先生凝視她的水晶球,低語道:“啊,古老的 vicuna 之靈對我說: Once upon a time, in a small moutain nestled in…”

你的腦海中開始產生懷疑。她的預測真實可信嗎?抱著懷疑和好奇的心態,你質疑她: “讓我們進行一次推理,驗證你的先見之明。”

然後,你將她的預言和原始提示的組合輸入模型。令人驚訝的是,模型的輸出與她的預測完全吻合……直到在 “village” 一詞出現偏差。

好吧,你可能意識到這個算命先生就是我們所說的 “speculative decoding”，一個小模型或美杜莎頭,可以為你草擬下一個幾個 tokens。

就這一輪而言,我們需要確定算命先生提供了多少正確的 tokens。

Question: 如果沒有像 speculative decode 的 parallel verification, 如何知道多少正確的 tokens?

Answer 1: 每次 inference 至少一個 token verification

Answer 2: 每次把多個 predict output tokens 輸入 input, 可以 verify 多個 tokens

你進行了一次單獨的推理,並注意到對於最近的提示標記 “:”，模型的輸出是 “Once”。這是模型自己的自迴歸生成,它處於平衡狀態。即使沒有她,你仍然知道對輸入 “:” 模型會輸出 “Once”!

這意味著她正確預測了 “upon a time, in a small” 是嗎?

但是等等!有些東西似乎不對勁。你驗證 “small” 是正確的。那麼對於輸入標記 “small” 的輸出呢? 由於之前的預測都保持平衡,模型對 “small” 的輸出 “village” 應該處於平衡狀態。

所以,即使她沒有正確預測 “village”,通過一次推理,你仍然可以為輸入 “small” 獲得正確的自迴歸結果!

考慮一下: 在算命先生的預測完全失準的極端情況下,模型仍然會根據提示自主生成 1 個正確的標記。

推理驗證本質上確保正確預測的下界為 1。換句話說,驗證保證其預測中至少有 1 個正確的標記。

因此,如果一切都失控了,驗證就只是常規的自迴歸推理。結果是,每個步驟只需要一次推理即可完成驗證和自迴歸過程。

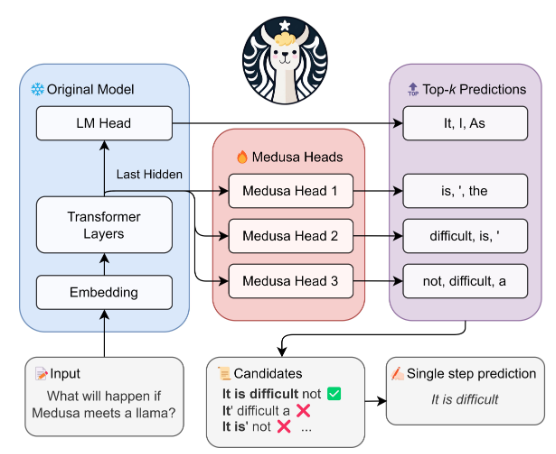
Medusa Head

那麼,美杜莎頭 (Medusa Head) 到底是什麼呢?

乍看之下,它們可能讓人聯想到原始架構中的語言模型頭,尤其是因果式Transformer模型的最後一層。

然而,有一個區別因素。美杜莎頭不僅預測下一個 token,還設計用於預測多個後繼 tokens。

這個有趣的特性源於區塊並行解碼方法。為了實現這一點,每個美杜莎頭的結構都是一個前饋神經網絡 (FFN),並且為了提高其效率,它還配備了殘差連接。

我們在下面列出美杜莎頭的結構,其中包含4個相同的模塊。每個模塊以一個殘差塊開頭,由一個線性層和一個SiLU激活函數組成,並以另一個線性層結尾,該線性層輸出分類結果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
ModuleList
    ResBlock 
        Linear (in: 4096, out: 4096)
        SiLU
    Linear (in: 4096, out: 32000)

    ResBlock
        Linear (in: 4096, out: 4096) 
        SiLU
    Linear (in: 4096, out: 32000)
    
    ResBlock
        Linear (in: 4096, out: 4096)
        SiLU
    Linear (in: 4096, out: 32000)

    ResBlock  
        Linear (in: 4096, out: 4096)
        SiLU
    Linear (in: 4096, out: 32000)
  • 參數量：(4096x4096 + 4096x32000 + 32000x4096) x 4 = 1.1B?

Reference