Acceptance-Rejection Sampling 接受拒絕採樣

Posted on | In

Source

接受拒絕採樣（Acceptance-Rejection Sampling） https://zhuanlan.zhihu.com/p/75264565

採樣：Rejection Sampling 和 MCMC https://zhuanlan.zhihu.com/p/598840708

https://www.jinghong-chen.net/an-mathematical-intuition-of-speculative-sampling

https://jaykmody.com/blog/speculative-sampling/. Speculative sampling code with resampling!

MCMC: Metropolis algorithm: https://www.youtube.com/watch?v=Jr1GdNI3Vfo&ab_channel=VeryNormal

前言

採樣的常見性和重要性不言而喻：全國人口信息普查、採樣去預估圓周率 等等。當然當紅炸子鷄生成式 AI 產生的文本、影像也是採樣的樣本。

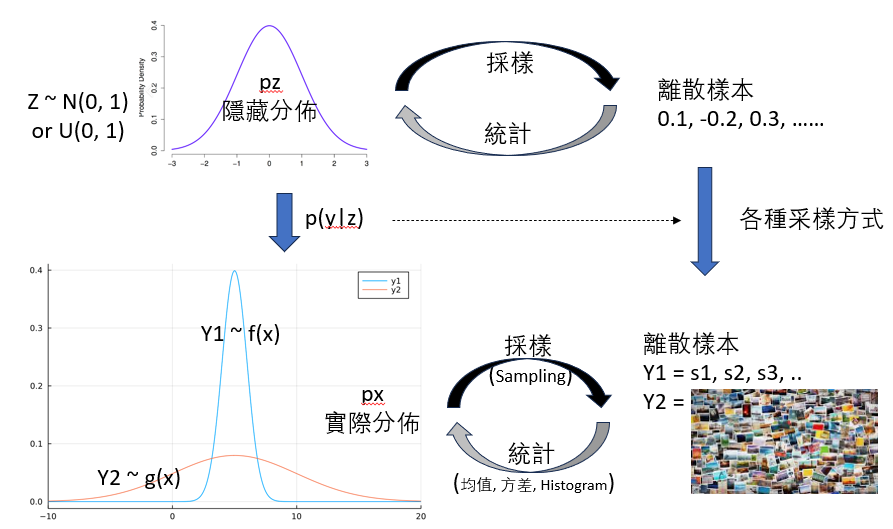
根據機率分佈產生的樣本也稱爲蒙特卡洛採樣 (Monte Carlo Sampling)。機率分佈一般是一個隱藏的假説，產生的樣本才是可以實際觀察到的，可以計算統計特性如

  • 優點：簡單直接，應用範圍廣。

    • 雖然簡單，但是如何產生符合機率分佈的樣本，是本文的重點。

  • 缺點：對於某些問題收斂速度較慢，且在高維情況下效率低下。

    • 對於强大的 GPU 可以大量平行計算，這個缺點已經不是的問題。

研究採樣的目的

有幾個目的：

  • 統計或 data mining (Samples -> PDF parameters) : 從一堆樣本得到統計資訊：例如平均值，方差，甚至更高階的資訊，相關性。
  • 分析式 AI (Sample -> Conditional PDF) : 一個樣本，得到其條件機率，常用於分類問題。
  • 生成式 AI (Samples -> New sample): 從一堆樣本產生新的樣本，常用於大語言模型。

PDF 機率分佈 = 樣本？

No! 不是等於，而是採樣。機率分佈 => 樣本

機率分佈函數是個隱藏的理論指導者，一般是連續函數 (uniform distribution, normal distribution)，可以用於理論計算，但是我們無法直接觀察。我們實際可以觀察的是離散的採樣樣本 (discrete sample).

How to dance between the continuous pdf and the discrete samples?

這本身有點抽象，不像數值分析的連續函數和離散序列有清楚的對應。

機率分佈函數是幕後的指揮家，讓生成的樣本（i.e. 採樣）服從一個已知假設的分佈。需要動動腦筋在連續的 pdf 和離散的樣本切換。

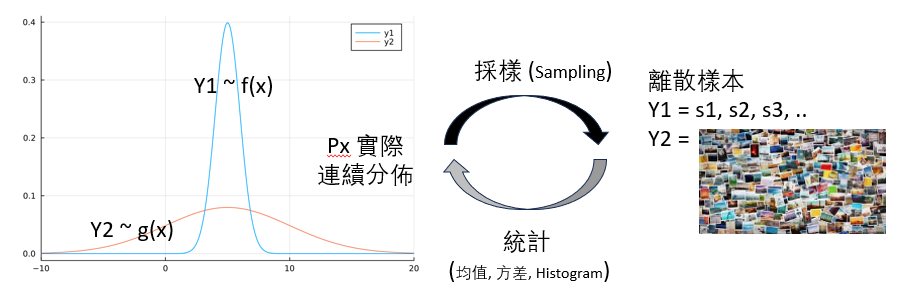
  • 這個過程稱爲 sampling (採樣)，如下圖從 PDF to (s1, s2, s3, …). 這是本文的重點。

  • 反之，產生的樣本如何驗證是否服從指揮？ (1) 可以簡單計算均值和方差是否正確，這是 1 或 2 階檢查；(2) 如果要更精確，可以計算 histogram 是否和 pdf 形狀一樣。這個驗證非常直觀。本文的重點在採樣。

  • 樣本不一定是數字 s1, s2, s3, …, 也可以是很多圖片 （其實圖片就是高維的數字）

image-20240602170253612

採樣的科學定義是啥？

我們知道現實世界的很多數據現象往往都是滿足一定的概率分佈的，我們用 PDF 去描述它。 比如最常見的正態分佈，越靠近均值的部分概率越大。在概率密度函數 (PDF) 已知的情況下，產生樣本是比較容易的事。

兩個 PDF 機率分佈相等 = 樣本相等(或無法分辨)？

兩個機率分佈相等最直覺的定義就是兩個 PDF 相等： $p_f(x) = p_g(x)$。兩個問題：

  • 正向：兩個 PDF 產生的樣本特性是否無法分辨？ Not really, 需要假設所有樣本之間是獨立事件！
  • 反向：兩個樣本特性無法分辨是否保證 PDF 相同？ Almost identical 幾乎相等。因為小的 glitches 不會影響樣本的統計特性。

正向應該比較可以理解。不過常常會混淆的是一個公平硬幣 B(p=0.5) (白努力分佈) 產生

  • $p_f(x)$: 0，1，1，1，0， 0， 1，0，1，0，0. ,… 均值：0.5，方差：1/12? 每個樣本之間都是獨立樣本，
  • $p_g(x)$:0，1，0，1，0，0，1，1，0 .. 均值：0.5，方差：1/12。也就是 $p_g(x)$ 和 $p_f(x)$ 的 $m$ 階統計特性 (m=1, 2, …) 都一樣。但是每一對數字都是 0, 1 或 1, 0. 我們可以說 $p_g(x) = p_f(x)$? yes? 但是差別是此處樣本之間有 100% 的相關性，這是 (marginal) PDF 沒有 capture 的特性！！
  • 但是 $p_g(x)$ 好像還是可以用來做所有 $p_f(x)$ 采樣的事情，只要不是看前後樣本相關性的工作？這也是 MCMC 可以用的基礎？

How to fix/show this problem?

但是如果有一個 machine: 可以產生 : 0, 1, 0, 1, 0, 1 或是 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 和 B(p=0.5) 似乎可以分辨。但是統計特性一樣？

應該要看 conditional on 之前的樣本 $p(x_n x_{n-1})$ or $p(x_n x_{n-1}, …., x_0)$​
所以可以看出 Q = 0， 1，0，1。.. 的 $p(x_n x_{n-1}=0) \ne q(x_n x_{n-1}=0)$, 條件的統計特性不同。

只有樣本之間 independent 才會化簡成 p(x). 更廣義是用 joint pdf p(x1, x2, …) = q(x1, x2, ….)

那如何定義這兩個 distribution 會有不同的結果？

$p_f(x_t, x_{t-1}) = p_f(x_t) p_f(x_{t-1})$

$p_g(x_t, t_{t-1}) = p(x_t) p(x_t \vert x_{t-1}) = p(x_t) * I(x_t, x_{t-1})$ where $I(x_t, x_t-1) = 0 \text{ or } 1$

很明顯, f, g 的 joint PDF 或是 conditional PDF 不相等。但是 marginal PDF, 就是對 $x_{t-1}$ 積分或和的 PDF 是完全一樣！

因此如果要利用到樣本之間的特性 (time domain, 例如計算樣本相關性)，則 marginal PDF 相等是不夠的 (i.e. MCMC 不行)。但如果和相關無關的統計特性，則可以用 marginal PDF 產生的樣本！

反之如果樣本特性無法分辨是非保證 (marginal) PDF 相同？

  1. almost identical. 因爲如果有個別點不同，不影響統計特性。
  2. 若是樣本之間相關性也無法分辨，代表 joint PDF 也是幾乎相等！不只是 marginal PDF!

已知 PDF 採樣

  • 常見的分佈 normal, uniform, exponential, etc. 可以直接呼叫函數產生

但是還存在着一些難以直接用 隨機採樣 這樣簡單的方法做到。 例如 double gamma distribution

  • 可以用已知的分佈例如 N(0, 1) 或 U(0, 1) 經過數學轉換產生。例如 inverse transformation sampling.

  • 也有使用更簡單的方法，例如 rejection-acceptance 方法採樣，速度比較快。

  • 還有使用比較先進的理論，例如 MCMC 採樣。

整體的架構如下。

image-20240602174834836

不同採樣方法

所以下面我們介紹幾種採樣方法，去解決這類無法簡單被隨機採樣得到的概率分佈 。

  • 逆變換採樣

  • Reject-accept sampling

  • Important sampling

  • Distribution transform sampling

  • MCMC (Monte Carlo Markov Chain) sampling

當處理複雜的概率分佈時，隨機採樣可能無法直接產生所需的樣本，因此我們需要使用一些更先進的採樣方法來解決這個問題。下面是幾種常用的採樣方法及其比較：

我們先從整數的 uniform distribution [0, N] 開始，因為 [0,N] 應該是最基本的隨機取樣。

  • 從 [0, N] 除以 N, 可以得到近似 [0, 1] 連續分佈的樣本。N 越大越連續。

基於轉換的採樣

概念很簡單，已知 pdf f(x), 是否可以從 [0, 1] 分佈隨機樣本，經過數學轉換得到近似 pdf f(x) 的樣本。

逆變換採樣 (Inverse Transform Sampling)

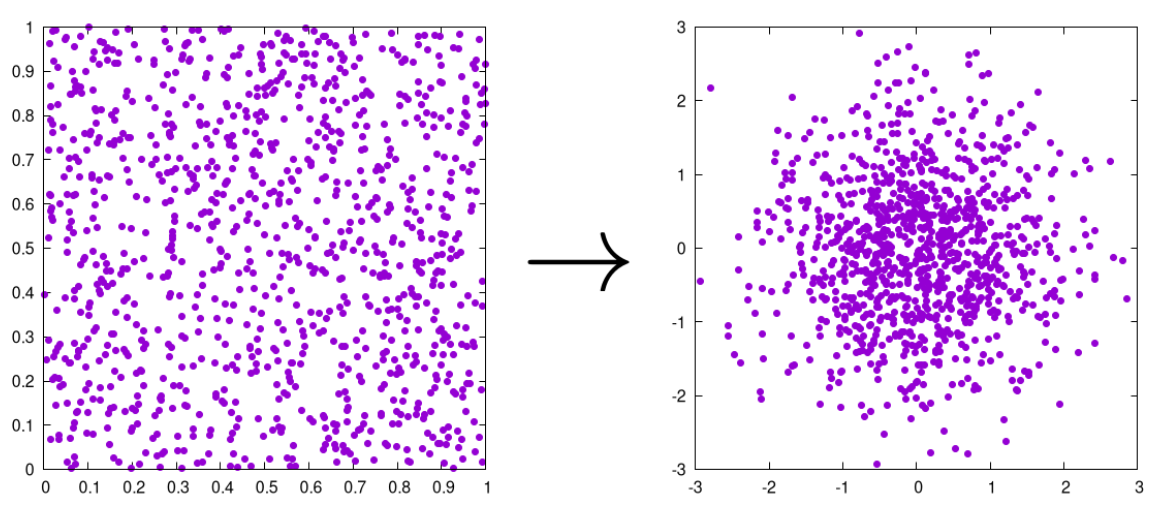
一個例子如下。從左側的 [0, 1] samples，經過 transform function G(x), 產生下方的 normal distribution sample N(0.5, 0.?).

  • 第一步是先找到 G(x)
  • 第二步是找 G(x) 的逆函數 $y = G(x) \to x = G^{-1} (x)$

一個問題是如何得到 G(x)?

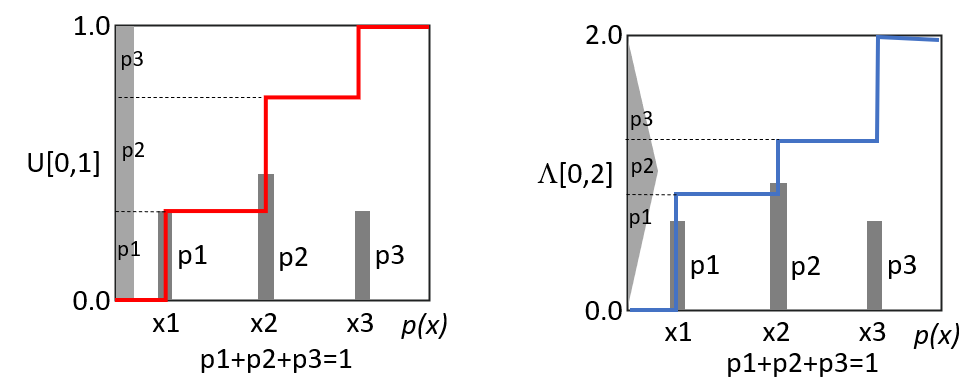
  • 我們先直觀看一個離散的 pmf: $p_f(x) = {p1}{x=x_1},{p2}{x=x_2},{p3}_{x=x_3}$​， 如下圖的柱狀圖。
  • 當左側是 $U[0, 1]$, 其面積就等於高度。所以 $G(x)$
    • 第一段的階梯 $G(x){x_1<x} = k_1 \text{ where }\int{0}^{k_1} U(0,1) = \sum p_f(x)_{x\le x_1} = p_1$
    • 第二段的階梯 $G(x){x_2<x} = k_2 \text{ where } \int{0}^{k_2} U(0,1) = \sum p_f(x)_{x\le x_2} = p1+p2$
    • 第三段的階梯 $G(x){x_3<x}= k_3 \text{ where } \int{0}^{k_3} U(0,1) = \sum p_f(x)_{x\le x_3} = p1+p2+p3=1$
    • 第二段減第一段，再到 ($x_1 \to x_2$) 無窮小極限：$G(x_2)-G(x_1) = k_2-k_1 \text{ where } \int_{k_2}^{k_1} U(0,1) = p_f(x) (x_2-x_1)$​
    • 因爲 $\int_{k_2}^{k_1} U(0,1) = U(0, 1) (k_2 - k_1) = (k_2 - k_1)$
    • $\Delta G(x) \approx p_f(x) \Delta x$. 所以 $G(x) = \int_{-\infty}^{x} p_f(x) dx$
    • 很明顯，當左側是 $U[0, 1]$, $G(x)$ 就是 $p_f(x)$​ 的 CDF。
  • 如果左側是 $\Lambda(0, 2)$, 例如兩個獨立 $U[0, 1]$​ 的和。我們稱爲這個 curve 為 $H(x)$ 顯然不是 CDF, 而是什麽？
    • 第一段的階梯 $H(x){x_1<x} = k_1 \text{ where }\int{0}^{k_1} \Lambda(0,2) = \sum p_f(x)_{x\le x_1} = p_1$
    • 第二段的階梯 $H(x){x_2<x} = k_2 \text{ where } \int{0}^{k_2} \Lambda(0,2) = \sum p_f(x)_{x\le x_2} = p1+p2$
    • 第三段的階梯 $H(x){x_3<x}= k_3 \text{ where } \int{0}^{k_3} \Lambda(0,2) = \sum p_f(x)_{x\le x_3} = p1+p2+p3=1$
    • 第二段減第一段，再到 ($x_1 \to x_2$) 無窮小極限：$H(x_2)-H(x_1) = k_2-k_1 \text{ where } \int_{k_2}^{k_1} \Lambda(0,2) = p_f(x) (x_2-x_1)$​
    • 因爲 $\int_{k_2}^{k_1} \Lambda(0,2) \approx \Lambda(0, 2) (k_2 - k_1)$ when $k_2 \to k_1$。 所以 $k_2 - k_2 \approx [\Lambda(x)]^{-1} (x_2 - x_1)$
    • $\Delta H(x) \approx p_f(x) [\Lambda(x)]^{-1} \Delta x$. 所以 $H(x) = \int_{-\infty}^{x} p_f(x) \Lambda^{-1}(x) dx$
    • 當左側是非 $U[0, 1]$, $H(x)$ 就是 $p_f(x)$​ 和左側 PDF 的倒函數 (不是逆函數)乘積的積分函數。

image-20240609191009612

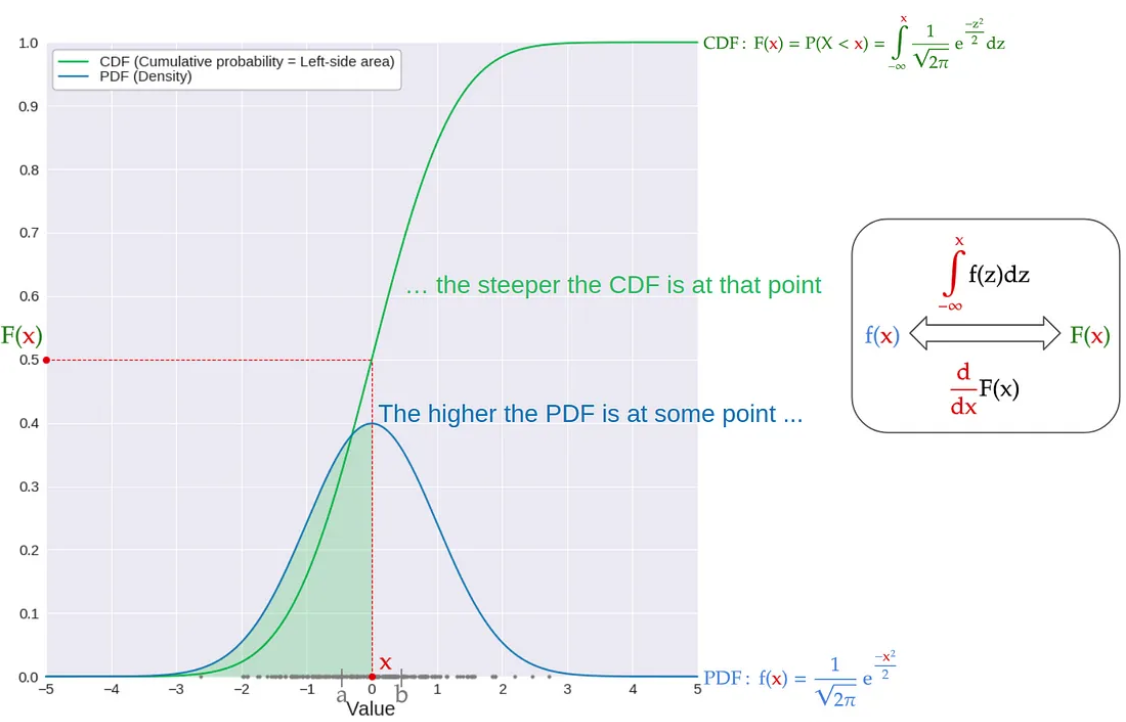
  • 連續的 PDF 只是以上離散分佈的無窮小的極限 case.
  • 從下方的 distribution 來看, 這個曲線就是 $f(x)$ 的 CDF, 也就是 $F(x) = \int_{-\infty}^{x} f(x)$. 為什麼？因為只有 CDF 才是單調遞增函數。重點是 $x$ 軸的一小段 $[x, x+\Delta x]$ 對應的 $y = F(x)$ 是 $[F(x), F(x+\Delta x)]$, 其密度是 $F(x+\Delta x)- F(x) = \int_{x}^{x+\Delta x} f(x) dx \approx f(x) \Delta x$. 這剛好是我們需要的！如下圖。
  • 從左方的 distribution 來看，這個曲線是 $F(x)$ 的反函數。
  • 所以 $U[0,1]$ 的 sample $x$, 經過 $F^{-1}(x)$ 的逆變換 (inverse transform) 的得到的 sample 剛好就是 $f(x)$ 的 sample.

img

优点：

  • 直接且簡單：只需計算逆 CDF，即可生成樣本。
  • 準確性高：完全遵循目標分佈。

缺点：

  • 計算複雜度高：對於復雜的分佈，逆 CDF 可能難以求解或計算成本高。
  • 僅適用於一維情況：需要知道分佈的 CDF 並能夠計算其反函數，對於高維分佈不太實用。

有名是從 $U[0, 1]$ 轉換成 $N(0, 1)$. Inverse transform sampling 雖然可以得到。 但是 Gaussian function 積分的反函數沒有 close form，計算複雜高，inverse transform 不會是 exact solution。

image-20240609094332586

數學表示 CDF of $\mathrm{N}(0,1)$ 是 error function. \(\begin{aligned} F(x)=A & =\frac{1}{2}+\frac{1}{2} \operatorname{erf}\left(\frac{x}{\sqrt{2}}\right) \\ 2 \mathrm{~A} & =1+\operatorname{erf}\left(\frac{\mathrm{x}}{\sqrt{2}}\right) \\ \operatorname{erf}\left(\frac{\mathrm{x}}{\sqrt{2}}\right) & =2 \mathrm{~A}-1 \\ \frac{x}{\sqrt{2}} & =\operatorname{erfinv}(2 \mathrm{~A}-1) \end{aligned}\)

結果 (沒有用) : \(\mathrm{F}^{-1}(\mathrm{~A})=\mathrm{x}=\sqrt{2} \operatorname{erfinv}(2 \mathrm{~A}-1)\)

因此我們需要更好的轉換。

分佈變換採樣 (Distribution Transform Sampling)

更複雜的座標變換，沒有一定的方法，都是 case-by-case. 我們看同樣的例子。利用 Box-Muller transform.

這個演算法是實際實施中最簡單的一個，並且在生成正態分佈的隨機數方面表現良好。

這個演算法非常簡單。我們首先從均勻分佈 $U(0,1)$ 中抽取兩個獨立的隨機樣本 $u_1, u_2$。然後，從它們生成兩個正態分佈的隨機變量 $z_1, z_2$。它們的值是： \(\begin{aligned} & z_1=\sqrt{-2 \ln \left(u_1\right)} \cos \left(2 \pi u_2\right) \\ & z_2=\sqrt{-2 \ln \left(u_1\right)} \sin \left(2 \pi u_2\right) \end{aligned}\) image-20240606231125431

其實這是利用平面座標轉換到極座標的特性。

  • $z_1^2 + z_2^2 = -2 \ln(u_1) \to u_1 = \exp(-\frac{z_1^2 + z_2^2}{2})$ 注意此時 $z_1, z_2$ 的範圍已經變成 $(-\infty, \infty)$
  • $\arctan (\frac{z_2}{z_1}) = 2 \pi u_2 \to u_2 = \frac{1}{2\pi}\arctan (\frac{z_2}{z_1})$

解釋：

  • 基於將複雜分佈轉換為易於採樣的分佈。
  • 常見方法包括 Box-Muller 變換，用於從均勻分佈生成正態分佈樣本。

比較：

  • 優點：可以利用簡單的變換來生成複雜分佈的樣本。
  • 缺點：變換過程可能不適用於所有分佈，且需要一定的數學推導。

基於塑形的採樣 - 拒絕接受採樣 (Reject-Accept Sampling)

Transform-based 的好處是所有 $U[0, 1]$​​ samples 經過數學計算都是有用的 samples. 也就是 acceptance rate = 100%. 另一類的思考是 reshape the distribution by reject-accept samples. 假設採樣很便宜，是否可以用選擇採樣的方法重塑分佈？

注意雖然 $U[0, 1]$ 是很容易的採樣，但並非所有的採樣都很便宜。例如 AI transformer output 的採樣就非常昂貴。

  Transform-base Reject-Accept base Important base
Method 接受所有樣本, 利用複雜數學轉換樣本符合目標分佈 利用簡單數學選擇接受部分樣本，重塑符合目標分佈 用數學方法選擇重要採樣？
Rationale 計算很便宜 採樣很便宜  
優化方向 如何找到最簡化的數學轉換公式 如何丟掉最少的樣本  

例一：如何用 U[0, 1] + reject-accept samples 逼近一個參數 $\pi$？

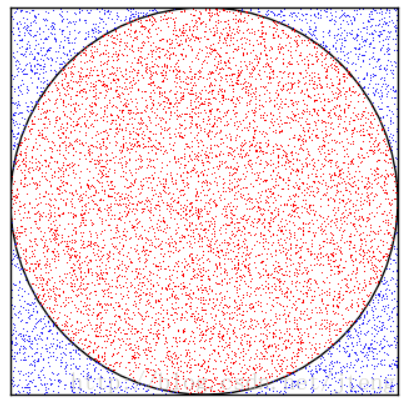
先举一个简单的例子介绍 Monte Carlo 方法的思想。假设要估计圆周率的值，选取一个边长为1的正方形，在正方形内作一个内切圆，那么我们可以计算得出，圆的面积与正方形面积之比为 $\frac{\pi}{4}$。现在在正方形内随机生成大量的点，$(x, y)$ where $x,y \in U[0,1]$ 如图1所示，落在圆形区域内的点标记为红色 ($x^2 + y^2 <1$)，在圆形区域之外的点标记为蓝色，samples = [R, B, R, R, B, R, B, …..]. 那么圆形区域内的点的个数与所有点的个数之比 $\frac{m}{N}$，$m$ 是 R 的樣本個數，N 是樣本總數。可以认为近似等于$\frac{\pi}{4}$。因此，Monte Carlo方法是通过随机采样的方式，以频率估计概率。所有 $\pi \sim \frac{4m}{N}$.

image-20240602223103701

例二：如何用 B(p=0.5) + reject-accept 產生 B(p=0.7)？

用最簡單的 Bernoulli distribution B(p1 = 0.5) 公平的硬幣，產生不公平分佈 B(p1=0.7) 的方法。

$p(x)$ 是 proxy/proposal/draft model. $q(x)$ 是 target model.

我們先直覺來看, $p(x) = B(p_1=0.5)$ 的樣本 $0, 1, 1, 0, 0, 1, 1, 0, …$ 基本是一半 0 一半 1. 要產生 $q(x) = B(p_1=0.7)$ 應該要 (1) 丟掉 0 和 1 的樣本，但是 0 的樣本丟的多。(2) 1 的樣本留下 (retain)。丟掉一些 0 的樣本 (drop)，再把一些 0 的樣本變成 1 (resample).

這兩種對應不同的 reject-accept sampling 方法。

image-20240607144343083

Method 1 (無條件丟樣本，丟多丟少而已)

  • 讓 $k\, p(x) = p’(x) \ge q(x)\text{ for all } x$. 此處我們取 $k = 2$, 所以 $p’(x)={1{x=0}, 1{x=1}} > q(x):{0.3{x=0}, 0.7{x=1}}$
  • 方法：保留機率: $q(x=\tilde{x})/p’(x=\tilde{x})$, 丟掉機率: $[p’(x=\tilde{x})-q(x=\tilde{x})]/p’(x=\tilde{x})$
  • 做法：
    • 若 $p(x)$ 生成的樣本 $\tilde{x} = 0$，保留 $\tilde{x}$ 的機率是 $\frac{q(x=0)}{p’(x=0)} = 0.3$，丟掉 $\tilde{x}$ 的機率是 $\frac{p’(x=0)-q(x=0)}{p’(x=0)} = 0.7$
    • 若 $p(x)$ 生成的樣本 $\tilde{x} = 1$，保留 $\tilde{x}$ 的機率是 $\frac{q(x=1)}{p’(x=1)} = 0.7$，丟掉 $\tilde{x}$ 的機率是 $\frac{p’(x=1)-q(x=1)}{p’(x=1)} = 0.3$
    • 剩下樣本 0 的機率就是 0.5x0.3=0.15, 樣本 1 的機率是 0.5x0.7=0.35. 所以 0 對 1 的比例是 0.15:0.35 = 3:7! 也就是 B(p1=0.7) = q(x)!
  • 剩下的樣本相對分佈比例如下。經過 normalization 就會得到 $q(x)$, QED。注意這可以拓展到任意的離散或是連續分佈！
\[p(x) \frac{q(x)}{p'(x)} = \frac{1}{k} q(x)\]
  • 丟掉的樣本的機率如下。這可以拓展到任意的離散或是連續分佈！
\[p(x=0) \frac{p'(x=0)-q(x=0)}{p'(x=0)} + p(x=1) \frac{p'(x=1)-q(x=1)}{p'(x=1)} = \frac{1}{k}\Sigma_j (p'(x_j)-q(x_j)) = \frac{k-1}{k}\]
  • 效率 = $1 - \frac{k-1}{k} = \frac{1}{k}$
  • 以本例 $k=2$ 來説，丟掉樣本的機率是 (2-1)/2 = 0.5,也就是丟掉 50% 樣本。效率是 50%

  • 如果要少丟一些樣本，就讓 $k$ 變小。$k_{\min} = 0.7/0.5 = 1.4$ , 此時丟掉樣本的機率是 (1.4-1)/1.4 = 2/7 ~ 29%. 所以丟掉約 29% 樣本。效率是 71%

  • 重點是丟掉樣本的機率只用簡單的 uniform distribution, 成本很低。但是丟掉的的樣本產生的成本可能很高。

解釋：

  • 適用於無法直接採樣但可以找到一個易於採樣的分佈 $p(x)$, proxy or proposal ，滿足 $ q(x) \leq k \cdot p(x) $，其中 $k$ 是一個常數。
  • 具體做法是：從 $p(x)$ 中生成樣本 $x$，再生成一個均勻隨機數 $ \gamma \in [0, 1] $。如果 $\gamma \leq \frac{q(x)}{k \cdot p(x)}$ ，則接受 $x$，否則重複以上步驟。

比較：

  • 優點：不需要知道目標分佈的 CDF。
  • 缺點：樣本丟掉的比例 $\frac{k-1}{k}$，效率 = $\frac{1}{k}$ 可能較低，特別是當 $k$​ 很大時。

如果不想丟掉樣本怎麽辦？那就把一部分 0 的樣本變成 1! 這是一個天才的想法！

Method 2 (多退少補)

  • 不做 scaling (i.e. no $k$).

  • 方法：
    • 若 $p(x=\tilde{x}) \le q(x=\tilde{x})$, 保留樣本。如下圖左的 $x_1$ 和 $x_2$.
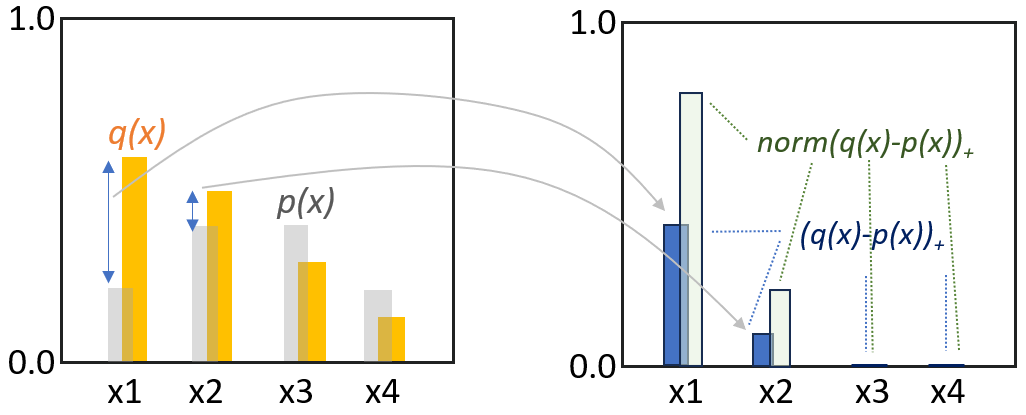
    • 若 $p(x=\tilde{x}) > q(x=\tilde{x})$, 多退少補。如下圖左的 $x_3$ 和 $x_4$. 如何多退少補？以 $x_3$ 爲例
      • 先從 $U[0, 1]$ 產生隨機值 $\gamma$, 和 $q(x_3) / p(x_3)$ 比較，如果 $\gamma < q(x_3)/p(x_3)$, 保留 $x_3$ 樣本。
      • 如果 $\gamma > q(x_3)/p(x_3),$（多退 $x_3$ 少補 $x_1, x_2$）重新取樣 (re-sample) based on $norm(q(x) - p(x))_+$​​​, 如下圖右的分佈。
      • 如果是 $x_4$​, 以上步驟完全一樣，（多退 $x_4$​ 少補 $x_1, x_2$​）。

      image-20240609220210270

  • 數學上可以再簡化一點 ，這是一般 speculative sampling 的寫法

    • 對於樣本 $\tilde{x}$, 從 $U[0, 1]$ 產生隨機值 $\gamma$ , 如果 $\gamma < \min\left(1, \frac{q(\tilde{x})}{p(\tilde{x})}\right)$，保留 $\tilde{x}$。

    • 如果 $\gamma > \min\left(1, \frac{q(\tilde{x})}{p(\tilde{x})}\right)$，重新取樣 (re-sample) based on $norm(q(x) - p(x))_+$。

  • 我們看 binary case 做法：

    • 若 $p(x)$ 生成的樣本 $\tilde{x} = 1$，因為 $p(x=1) = 0.5 < q(x=1) = 0.7$, 保留 (retain) $\tilde{x} = 1$
    • 若 $p(x)$ 生成的樣本 $\tilde{x} = 0$，因為 $p(x=0) = 0.5 > q(x=0) = 0.3$, 所以要保留 $q(x=0)=0.3$ 的機率 0 樣本，另外一部分 $p(x=0)-q(x=0)=0.5-0.3=0.2$ 的機率 0 樣本轉成 1。這個過程成爲重取樣 (resample)。
    • 問題是如何計算重取樣的比例，多少樣本還是保留 0, 多少 0 樣本轉換成 1 樣本？ 就是從新 normalize $[q(x=0), p(x=0)-q(x=0)] = [0.3, 0.2]$, 重新 normalize $[0.3/0.5, 0.2/0.5] = [0.6, 0.4]$. 也就是保留 60% 的 0 樣本， 40% 的 0 樣本轉換成 1 樣本。
    • Resampling (重取樣): (1) $(p(x)-q(x))$, (2) normalization.
    • 因此最後 0 樣本有 $p(x=0) \frac{q(x=0)}{p(x=0)-q(x=0)+q(x=0)} = 0.5 \times 0.6 = 0.3 = q(x=0).$
    • 而 1 樣本有 $p(x=1) + p(x=0) \frac{p(x=0)-q(x=0)}{p(x=0)-q(x=0)+q(x=0)} = 0.5 + 0.5 \times 0.4 = 0.7 = q(x=1).$

  • 以上的做法並不好，因爲無法直接推廣到 binary distribution 以外的 case！關鍵在於重取樣把目前多的機率 ($p(x=0) > q(x=0)$) 也考慮進來。可以推廣到 multiple outcomes 的做法是分成兩步走。

    • 先決定有多少 $\tilde{x} = 0$ 的樣本要保留：q(x=0) / p(x=0) = 0.3/0.5 = 3/5. 我們取樣 $\gamma$ from $U[0,1]$。 如果 $\gamma < 3/5=0.6$, 保留這個 $\tilde{x} = 0$. 也就是 60% 機率保留這個 $\tilde{x} = 0$。 如果 q(x=0) = p(x=0), 就是極限的例子，保留全部 $\tilde{x} =0 $ 樣本。
    • 若是 $\gamma > 3/5$, 也就是 40% 機會，需要重新取樣 (resample). 不過這裏可以省略重取樣，因爲只能取樣 1. 也就是 $\gamma > 3/5$, 就直接把 $\tilde{x}$ 改成 1!
    • 數學上 $(q(x) - p(x))+ = [0{x=0}, 0.2{x=1}]$. 經過 normalization, $norm(q(x) - p(x))+ = [0{x=0}, 1{x=1}]$

  • 看起來有點脫褲子放屁，結果是一樣。實際上分兩步走對於 multiple outcomes 有 (數學上的) 好處。例如以上 4 個 outcomes 的例子。

    • 所有 $\tilde{x} = x_1$ 和 $\tilde{x} = x_2$ 的樣本都保留，因爲 $p(x_1) < q(x_1)$ 和 $p(x_2) < q(x_2)$
    • 所有 $\tilde{x} = x_3$ 和 $\tilde{x} = x_4$ 的樣本都有 $\gamma_3 = q(x_3)/p(x_3)$ 和 $\gamma_4 = q(x_4)/p(x_4)$ 的機率保留，因爲 $p(x_3) > q(x_3)$ 和 $p(x_4) < q(x_4)$​
    • 對於 $\tilde{x} = x_3$ 並且 $\gamma_3 > q(x_3)/p(x_3)$ 的樣本以及同樣情況的 $x_4$ 樣本，依照 $norm(q(x) - p(x))_+$ 重取樣變成 $x_1$ 或是 $x_2$.

  • 重點 1 是沒有丟掉任何樣本。

  • 重點 2 是 $\gamma$​ 是一個簡單的 binary outcome uniform 采樣。重取樣 (resampling) 也是 binary or multiple otucomes uniform distribution 采樣。

Appendix 證明以上的 procedure 可以讓一個 $p(x)$ distribution + Reject-Accept Sampling 變成和 q(x) distribution 相同的機率分佈。如前所述，如果兩個機率分佈相同，代表兩者產生的樣本是無法分辨。

重要性採樣 (Important Sampling)

重要性採樣是一種蒙特卡洛方法，用於從難以直接採樣的目標分佈中估計期望值。其核心思想是從一個易於採樣的提議分佈中生成樣本，並使用權重來調整這些樣本，使其符合目標分佈。

解釋：

  • 用於改進蒙特卡洛積分估計的效率。
  • 具體做法是：選擇一個易於採樣的分佈 ( q(x) ) 作為“提議分佈”，然後使用 ( p(x) / q(x) ) 作為權重來調整樣本。

比較：

  • 優點：對於高維積分的計算非常有效。
  • 缺點：需要選擇合適的提議分佈 ( q(x) )，否則可能導致估計的方差非常大。

基於轉換的採樣：MCMC 採樣 (Markov Chain Monte Carlo Sampling)

https://www.youtube.com/watch?v=Jr1GdNI3Vfo&ab_channel=VeryNormal

描述： MCMC 採樣是一種利用馬爾可夫鏈生成從目標分佈中獨立樣本的方法。常見算法包括 Metropolis-Hastings 和 Gibbs 採樣。其基本思想是通過構建一個馬爾可夫鏈，該鏈的穩態分佈即為目標分佈。

解釋：

  • 適用於高維分佈。
  • 基於構建一個馬爾可夫鏈，其穩態分佈為目標分佈。常見方法包括 Metropolis-Hastings 演算法和 Gibbs 取樣。

比較：

  • 優點：非常適合高維分佈和複雜分佈的採樣。
  • 缺點：需要長時間運行以達到穩態，並且需要診斷收斂性。

總結

  • 逆變換採樣 適合簡單一維分佈，但要求已知的 CDF 反函數。

  • 分佈變換採樣 通過數學變換簡化採樣過程，但適用性有限。

  • 拒絕接受採樣 對分佈的要求較少，但效率可能低。

  • 重要性採樣 在合適的提議分佈下非常高效，但選擇提議分佈是個挑戰。

  • MCMC 採樣 是高維和複雜分佈採樣的強大工具，但需要診斷收斂。

採樣方法 描述 優點 缺點
逆變換 使用逆 CDF 生成樣本 直接且簡單；準確性高 計算複雜度高；僅適用於一維情況
拒絕接受 從候選分佈生成樣本並根據接受概率決定是否接受 靈活性高；適用於多維分佈 效率低下；計算成本高
Important 使用權重調整提議分佈樣本以估計目標分佈的期望值 高效；靈活 權重不穩定；需要良好的提議分佈
分佈轉換 使用變換將基本分佈轉換為目標分佈 高效；準確性高 受限於變換函數；適用範圍有限
MCMC 使用馬爾可夫鏈生成目標分佈樣本 適用於複雜和高維分佈；靈活性高 收斂速度慢；依賴初始值

這些採樣方法各有其優缺點，選擇哪種方法取決於具體的應用場景和需求。例如，對於需要高準確性的情況，逆變換採樣是理想選擇，而對於高維和複雜分佈，MCMC 採樣則更為合適。

未知 PDF 採樣，但有樣本

再來是最難的問題，我們不知道 PDF! 但是我們有一堆的樣本 (samples). 問題變成如何產生新的樣本符合原來的機率分佈。

這就是深度學習以及生成式 AI 大顯身手的地方。

深度學習

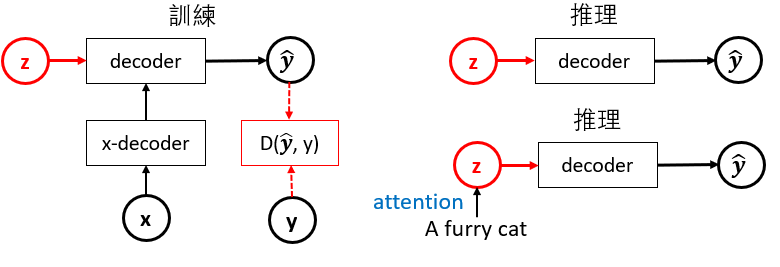
簡單來説就是用神經網路模擬 $q(z y)$ 和 $p(y z)$, 也就是 encoder and decoder.

利用一堆的樣本訓練 encoder and decoder. 再用 random number + decoder 產生新的樣本。

對於分析式 AI 就有好幾個 PDFs (狗，貓, …), 使用 encoder 訓練 labeled data. 不用 decoder.

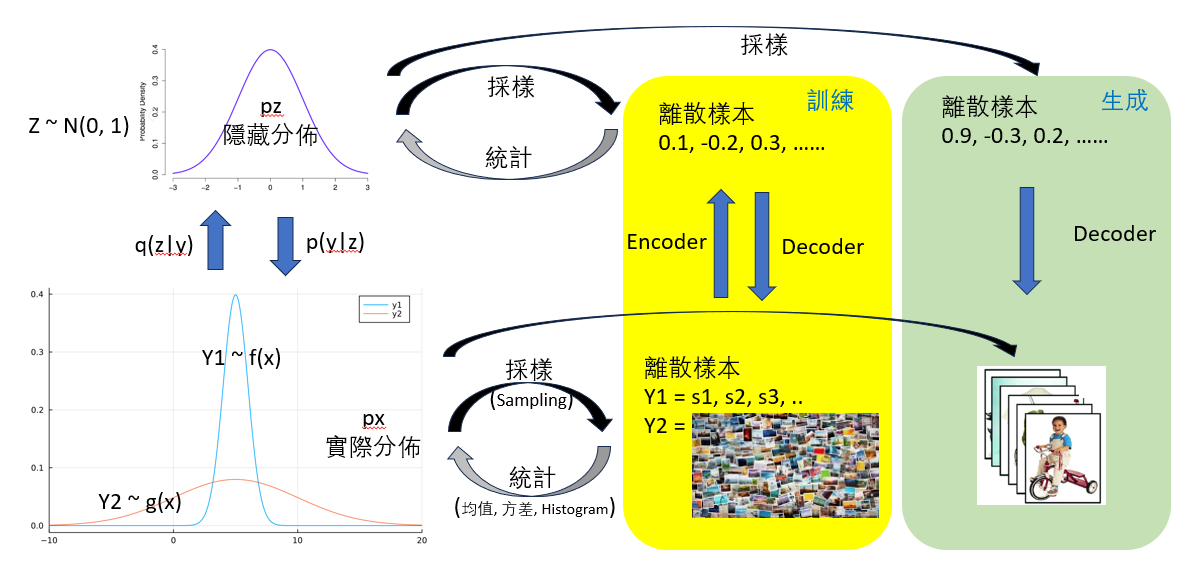
image-20240602175732605

簡單説就是用訓練好的 decoder, 加上 normal distribution 產生的隨機樣本或是加上 attention 的 input, 生成新的樣本。

image-20240602222249155

Appendix

拒絕接受採樣 (Reject-Accept Sampling)

Method 1 (無條件丟樣本，丟多丟少而已)

简单分布的采样，如均匀分布、高斯分布、Gamma分布等，在计算机中都已经实现，但是对于复杂问题的采样，就需要采取一些策略， 拒绝采样就是一种基本的采样策略，其采样过程如下。

  1. 给定一个概率分布 $q(z)$

  2. 要对该分布进行拒绝采样，首先借用一个简单的参考分布 (Proposal distribution or Proxy distribution)，记为 $p(z)$，该分布的采样易于实现，如均匀分布、高斯分布。然后引入常数 $k$，使得对所有的的 $z$，满足 $k\,p(z)> q(z)$，如下图所示，红色的曲线为 $q(x)$，蓝色的曲线为 $k\,p(z)$。

在每次采样中，首先从 $p(z)$ 采样一个数值 $z_0$，然后在区间 $[0,k\,p(z_0)]$ 进行均匀采样，得到 $u_0$。如果 $u_0< q(z)$，则保留该采样值，否则舍弃该采样值。最后得到的数据就是对该分布的一个近似采样。

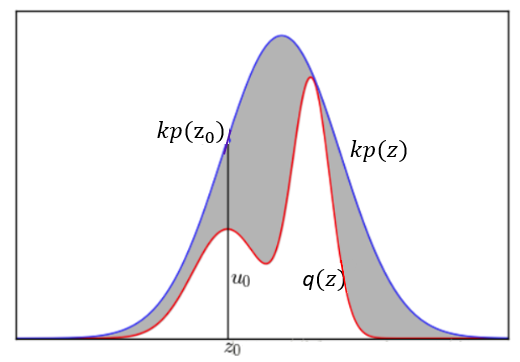
image-20240610230043295

每次采样的接受概率计算如下：

$P(\text{accept})=\int \frac{q(z)}{k p(z)} p(z) d z=\frac{1}{k} \int q(z) d z = \frac{1}{k}$

所以，为了提高接受概率，防止舍弃过多的采样值而导致采样效率低下， $k$ 的选取应该在满足 $kp(z)≥q(z)$ 的基础上尽可能小。

拒绝采样问题可以这样理解：

$q(z)$ 与轴之间的区域为要估计的问题，类似于上面提到Monte Carlo方法中的圆形区域，$kp(z)$与轴之间的区域为参考区域，类似于上面提到的正方形。由于与轴之间的区域面积为$k$，所以，与轴之间的区域面积除以$k$​即为对的估计。在每一个采样点，以为界限，落在曲线以下的点就是服从分布的点。$1/k$ 就相當與 $\pi/4$.   

Method 2 (多退少補)

數學證明有點複雜。不過原理和上文一樣！

$\begin{aligned} P\left(\text{target} = x_i\right)= & \sum_j P\left(\text{target}= x_i \mid \text{draft} = x_j\right) P\left(\text{draft} = x_j\right)
= & P\left(\text {target} = x_i \mid \text{draft} = x_i\right) P\left(\text{draft} = x_i\right) +\sum_{j \neq i} P\left(\text {target} = x_i \mid \text{draft} = x_j\right) P\left(\text{draft} = x_j\right) \end{aligned}$

Let $P(\text{target} = x_i) = P_T(x_i)$ and $P(\text{draft} = x_i) = P_D(x_i)$​

  • $P\left(\text {target} = x_i \mid \text{draft} = x_i\right)$ 代表保留 $x_i$ 樣本的機率： $P_T(x_i) > P_D(x_i)$：$P\left(\text {target} = x_i \mid \text{draft} = x_i\right) = 1$​ $P_T(x_i) < P_D(x_i)$：$P\left(\text {target} = x_i \mid \text{draft} = x_i\right) = \frac{P_T(x_i)}{P_D(x_i)}$

    綜合兩者： $\begin{aligned} P\left(\text {target} = x_i \mid \text{draft} = x_i\right) = \min\left(1, \frac{P_T(x_i)}{P_D(x_i)}\right) \end{aligned}$​

  • $P_{i\ne j}\left(\text {target} = x_i \mid \text{draft} = x_j\right)$ 代表 $x_j$ 重取樣成 $x_i$​ 樣本的機率： $P_T(x_j) > P_D(x_j)$：$P_{i\ne j}\left(\text {target} = x_i \mid \text{draft} = x_j\right) = 0$​, $x_j$ 自己不夠，無法補 $x_i$ \(\begin{aligned} P_T(x_j) < P_D(x_j) &: P_{i\ne j}\left(\text {target} = x_i \mid \text{draft} = x_j\right)\\ &= (1 - \frac{P_T(x_j)}{P_D(x_j)})\, normal(P_T(x_i)-P_D(x_i))_+ \\ &= (1 - \frac{P_T(x_j)}{P_D(x_j)})\, normal(\max(0, P_T(x_i)-P_D(x_i))) \end{aligned}\) 綜合兩者：

    $\begin{align} &P_{i\ne j}\left(\text {target} = x_i \mid \text{draft} = x_j\right)\ &= \left(1-\min\left(1, \frac{P_T(x_j)}{P_D(x_j)}\right)\right)\,normal(\max(0, P_T(x_i)-P_D(x_i)))\ &= \max\left(0, \frac{P_D(x_j)-P_T(x_j)}{P_D(x_j)}\right)\,normal(\max(0, P_T(x_i)-P_D(x_i))) \end{align}$

帶入 (2) 式：$P(\text{target} = x_i)$

$\begin{aligned} =& \min \left(1, \frac{P_{\mathrm{T}}\left(x_i\right)}{P_{\mathrm{D}}\left(x_i\right)}\right) P_{\mathrm{D}}\left(x_i\right) + \sum_{j\ne i}\left(1-\min \left(1, \frac{P_{\mathrm{T}}\left(x_j\right)}{P_{\mathrm{D}}\left(x_j\right)}\right)\right) \frac{\max \left(0, P_{\mathrm{T}}\left(x_i\right)-P_{\mathrm{D}}\left(x_i\right)\right)}{\sum_{k} \max \left(0, P_{\mathrm{T}}\left(x_k\right)-P_{\mathrm{D}}\left(x_k\right)\right)} P_{\mathrm{D}}(x_j) \ = & \min \left(P_{\mathrm{D}}\left(x_i\right), P_{\mathrm{T}}\left(x_i\right)\right) + \max \left(0, P_{\mathrm{T}}\left(x_i\right)-P_{\mathrm{D}}\left(x_i\right)\right) \frac{\sum_{j\ne i}\left(P_{\mathrm{D}}\left(x_j\right)-\min \left(P_{\mathrm{D}}\left(x_j\right), P_{\mathrm{T}}\left(x_j\right)\right)\right.}{\sum_k \max \left(0, P_{\mathrm{T}}\left(x_k\right)-P_{\mathrm{D}}\left(x_k\right)\right)} \ = & \min \left(P_{\mathrm{D}}\left(x_i\right), P_{\mathrm{T}}\left(x_i\right)\right) + \max \left(0, P_{\mathrm{T}}\left(x_i\right)-P_{\mathrm{D}}\left(x_i\right)\right) \frac{\sum_{j\ne i} \max \left(0, P_{\mathrm{D}}\left(x_j\right)-P_{\mathrm{T}}\left(x_j\right)\right)}{\sum_{k} \max \left(0, P_{\mathrm{T}}\left(x_k\right)-P_{\mathrm{D}}\left(x_k\right)\right)} \ = & \min \left(P_{\mathrm{D}}\left(x_i\right), P_{\mathrm{T}}\left(x_i\right)\right)+\max \left(0, P_{\mathrm{T}}\left(x_i\right)-P_{\mathrm{D}}\left(x_i\right)\right) \ = & P_{\mathrm{T}}\left(x_i\right) \end{aligned}$​

If $P_T(x_i) < P_D(x_i)$ : $= P_T(x_i)$

If $P_T(x_i) > P_D(x_i)$: $= P_D(x_i) + (P_T(x_i) - P_D(x_i)) \frac{\sum_{j} \max \left(0, P_{\mathrm{D}}\left(x_j\right)-P_{\mathrm{T}}\left(x_j\right)\right)}{\sum_{k} \max \left(0, P_{\mathrm{T}}\left(x_k\right)-P_{\mathrm{D}}\left(x_k\right)\right)} $​

因為 $\max(0, P_D(x_i) - P_T(x_i) ) = 0$ 可以把上式 $j \ne i$ 移除！

假設 $P_T(x_k) > P_D(x_k)$ for $k = 1, 2, …, m$ and

$P_T(x_k) < P_D(x_k)$ for $k = m+1, …, n$​

${\sum_{j} \max \left(0, P_T\left(x_j\right)-P_D\left(x_j\right)\right)} = \sum_{1}^m (P_T(x_k) - P_D(x_k))$

${\sum_{j} \max \left(0, P_D\left(x_j\right)-P_T\left(x_j\right)\right)} = \sum_{m+1}^n (P_D(x_k) - P_T(x_k)) = 1 - \sum_1^m P_D(x_k) - [1 - \sum_1^m P_T(x_k)]$

$= \sum_1^m (P_T(x_k) - P_D(x_k))$