Geometric Algebra (GA) Introduction and Application

Posted on | In

Reference

Question

Complex eigenvalue 代表什麽意義 in GA?

(1) Geometric Algebra in 2D - Linear Algebra and Cramer’s Rule - YouTube : from GA viewpoint of linear algebra

Introduction

兩個角度看 Geometric Algebra (GA): (1) 歷史角度和 (2) 幾何角度。

歷史角度：

  • 笛卡爾開創結合幾何和代數的先河，引入笛卡爾坐標系。
  • 高斯引入 (2D) 複數平面，成功的賦予複數 $i$ 幾何意義，就是逆時針旋轉 90 度。一個複數平面的 vector $(x,y) = x + iy$， 可以加、減、乘、除一個複數得到新的 vector. 加和減對應 vector 的加法和減法。更驚奇的是乘法和除法。乘或除一個實數對應 vector 的放大或縮小。乘或除虛數 $i$ 卻是對應 vector 逆時針或順時針旋轉 90 度。如果是乘或除複數就是對應 vector 的縮放和旋轉 (scale and rotation). 黎曼進一步解析延拓，開創了複變分析的數學分支。
  • 很自然的下一步就是拓展到 (3D) 空間幾何。最初 Hamilton (1843) 的 quaternion 似乎是衆望所歸。不過有幾個問題：
    • The basis vectors square to -1 and not +1, i.e. $i^2 = j^2 = k^2 = ijk = -1$ and $i j = k$ 因此很多物理量變得非常奇怪，例如 kinetic energy: $\frac{1}{2} m \boldsymbol{v}^2 = - \frac{1}{2} m \boldsymbol{v} ^2$
      • Why 2D 複數沒有這個問題? 因爲 2D 用 complex conjugate $\frac{1}{2} m \boldsymbol{v} \boldsymbol{v}^* = \frac{1}{2} m \boldsymbol{v} ^2 = \frac{1}{2} m (x^2 + y^2)$
      • 3D quaternion 沒有 complex conjugate?
    • All operations are non-commutative (rotation is non-commutative?)
    • 需要額外加上第四個 scalar component, $a$, 多餘且無意義。
    • 最主要的問題是 quaternion 的 basis vectors, $i, j, k$, 是對應 $x, y, z$ 軸的 90 度旋轉，少了 vector 的 scaling (or projection, or similarity) basis!? 從 group theory 角度，quaternion 只有 address su(2) symmetry.

image-20221203214012485

  • 因此 Gibbs/Heaviside 的 vector $[x, y, z] = x e_i + y e_j + z e_k$, where $e_i^2 = e_j^2 = e_k^2 = 1$ 成爲主流迄今。

    • 此時相反變成沒有 rotation 的 basis! 例如 $[x, y, 0]$ 的 vector 無法乘、除一個 vector 產生 $e_k$ 方向的 component!

    • Tensor 的 covariant and contravariant coordinate 無法解決這個問題！Really? TBC.

    • 解決這個問題需要定義新的 vector multiplication, 就是外積或是 curl, $A \times B$ or $\nabla \times B$ operations.

    • Vector product 定義：

      • Inner product 内積是一個 scalar

        • (坐標系無關) 幾何：大小 $\vec{u} \cdot \vec{v} = |\vec{u}| | \vec{v}| \cos(\theta)$ , 沒有方向。物理意義就是$u, v$ 的相似度。

        • $\vec{u} \cdot \vec{v} = (a_1 e_1 + b_1 e_2 + c_1 e_3)\cdot(a_2 e_1 + b_2 e_2 + c_3 e_3) = a_1 a_2 +b_1 b_2 + c_1 c_2$

      • Cross product 叉積是一個 vector

        • (坐標系無關) 幾何 ：大小 $\vec{u} \times \vec{v} = |\vec{u}| | \vec{v}| \sin(\theta)$ , 方向是 normal direction。物理意義就是 $u, v$ 圍的面積。

        • $\vec{u} \times \vec{v} = (a_1 e_1 + b_1 e_2 + c_1 e_3)\times (a_2 e_1 + b_2 e_2 + c_2 e_3) = (b_1 c_2 - c_1 b_2) e_1 + (c_1 a_2 - a_1 c_2) e_2 + (a_1 b_2 - b_1 a_2) e_3 $ where $e_i \times e_i = 0 $ and $e_i \times e_j = e_k$. $B \times A = -A \times B$

      • Outer product 外積是一個 bi-vector: 方向是第一 vector 到第二 vector 的手性方向

        • (坐標系無關) 幾何：大小 $\vec{u} \wedge \vec{v} = |\vec{u}| | \vec{v}| \sin(\theta)$ , 物理意義就是 $u, v$ 圍的面積。方向是 $i$ (2D)
        • $\vec{u} \wedge \vec{v} = (a_1 e_1 + b_1 e_2 + c_1 e_3)\wedge (a_2 e_1 + b_2 e_2 + c_2 e_3) = (b_1 c_2 - c_1 b_2) e_2 e_3 + (a_1 c_2 - a_2 c_1) e_1 e_3 + (a_1 b_2 - b_1 a_2) e_1 e_2 $ where $e_i \wedge e_i = 0 $. $B \times A = -A \times B$ 到此都和 cross product 一樣
        • 3D $e_1 e_2 e_3 = i$ 所以 $\vec{u} \wedge \vec{v} = (b_1 c_2 - c_1 b_2) e_2 e_3 + (c_1 a_2 - a_1 c_2) e_1 e_3 + (a_1 b_2 - b_1 a_2) e_1 e_2 = i \vec{u} \times \vec{v} $

      • 以上看起來 cross product 好像和 outer product 一樣？ No, there are several difference

        • 大小是一樣

        • 叉積得到 vector, 外積得到 bi-vector.

        • 叉積在 2D 不存在，外積在 2D 等價與複數運算。

        • 在 2D 沒有定義 cross product, 但可以定義 outer product (引入 $i$)

        • 在 3D cross product 和 outer product 的特性不同。 cross product 仍然是一個 vector, outer product 是 bi-vector.

        • vector 的手性和 bi-vector 不同，也無法相加。

        • 在 3D space, 可以把 cross product 和 outer product 用 $\vec{u} \wedge \vec{v} = i \vec{u} \times \vec{v} $ link 起來！

      • Caveat: 不像 Gauss 定義的 2D complex plane, 複數可以加、減、乘、除。以上的 vector space inner product 或 cross-product 沒有逆運算！ 後面會提到 GA product 有逆運算 Tensor 有除法嗎? TBC

  • **Clifford 定義 geometric vector product (幾何積, 乘法): **

    • (坐標系無關) 幾何：**$\vec{u} \vec{v} = \vec{u} \cdot \vec{v} + \vec{u} \wedge \vec{v} = |\vec{u}| | \vec{v}| (\cos(\theta)+i\sin(\theta)) = |\vec{u}| | \vec{v}| \exp(i\theta)$ **

    • $\vec{u} \cdot \vec{v}$ 是標準内積。 $\vec{u} \wedge \vec{v}$ 是外積！GA 就是内積加上“外積”，可以推導一些特性：

      • $\vec{u} \vec{u} = \vec{u} \cdot \vec{u} = |\vec{u}|^2 \to \vec{u}^{-1} = \frac{\vec{u}}{|\vec{u}|^2}$

      • $\vec{u} \vec{v} = \vec{u} \cdot \vec{v} + \vec{u} \wedge \vec{v} = |\vec{u}| | \vec{v}| \exp(i\theta) \to \vec{v} \vec{u} = \vec{u} \cdot \vec{v} - \vec{u} \wedge \vec{v} = = |\vec{u}| | \vec{v}| \exp(-i\theta) = (\vec{u} \vec{v})^* $ 其實就是 conjugate operation.

      • $\vec{u} \cdot \vec{v} = \frac{1}{2}(\vec{u} \vec{v} + \vec{v} \vec{u}) \text{ and } \vec{u} \wedge \vec{v}= \frac{1}{2}(\vec{u} \vec{v} - \vec{v} \vec{u})$

  • **比較有趣的是 Bivector product? 3D: ** $\vec{U} \vec{V} = \vec{U} \cdot \vec{V} + \vec{U} \wedge \vec{V}$

  • **見後面討論 **

GA Basis

我們落實到直角坐標系。Q: 需要限制在直角坐標系嗎?

  • $e_i e_i = 1$ (scalar) and 定義 bi-vector: $e_i e_j = - e_j e_i$ when $i \ne j$
  • 我們可以檢查 GA 的 vector 乘 vector, 先看 2D. 在 2D 情況：$\hat{x}\hat{y} = i$
\[\begin{aligned} \vec{u} =& a_1 \hat{x}+b_1 \hat{y} \\ \vec{v} =& a_2 \hat{x}+b_2 \hat{y} \\ \vec{u} \vec{v} =& \left(a_1 \hat{x}+b_1 \hat{y}\right)\left(a_2 \hat{x}+b_2 \hat{y}\right) \\ =& a_1 a_2 \hat{x} \hat{x}+a_1 b_2 \hat{x} \hat{y} \\ & b_1 a_2 \hat{y} \hat{x}+b_1 b_2 \hat{y} \hat{y} \\ \vec{u} \vec{v} =& a_1 a_2+b_1 b_2+\left(a_1 b_2-b_1 a_2\right) \hat{x} \hat{y} \end{aligned}\]
  • 我們可以檢查 GA 的 vector 乘 vector, 在 3D 情況：$\hat{x}\hat{y}\hat{z} = i$
\[\begin{aligned} \vec{u} =& a_1 \hat{x}+b_1 \hat{y}+c_1 \hat{z} \\ \vec{v} =& a_2 \hat{x}+b_2 \hat{y}+c_2 \hat{z} \\ \vec{u} \vec{v} =& \left(a_1 \hat{x}+b_1 \hat{y}+c_1 \hat{z}\right)\left(a_2 \hat{x}+b_2 \hat{y}+c_2 \hat{z}\right) \\ =& a_1 a_2 \hat{x} \hat{x}+a_1 b_2 \hat{x} \hat{y}+a_1 c_2 \hat{x} \hat{z} \\ +& b_1 a_2 \hat{y} \hat{x}+b_1 b_2 \hat{y} \hat{y}+b_1 c_2 \hat{y} \hat{z} \\ +& c_1 a_2 \hat{z} \hat{x}+c_1 b_2 \hat{z} \hat{y}+c_1 c_2 \hat{z} \hat{z} \\ \vec{u} \vec{v} =& a_1 a_2+b_1 b_2+c_1 c_2+\left(a_1 b_2-b_1 a_2\right) \hat{x} \hat{y}+ \left(b_1 c_2-c_1 b_2\right) \hat{y} \hat{z}+\left(a_1 c_2-c_1 a_2\right) \hat{x} \hat{z} \end{aligned}\]
  • vector 乘 vector 得到 scalar + bivector. 我們可以定義任何 bivector 乘 bivector 或是 vector 得到更多的變化。
  • In general
    • 2D multivector: $a + b \hat{x} + c \hat{y} + d \hat{x}\hat{y}$
    • 3D multivector: $a + b \hat{x} + c \hat{y} + d \hat{z} + e \hat{x}\hat{y} + f \hat{y}\hat{z} + g \hat{x}\hat{z} + h \hat{x}\hat{y}\hat{z}$

幾何角度

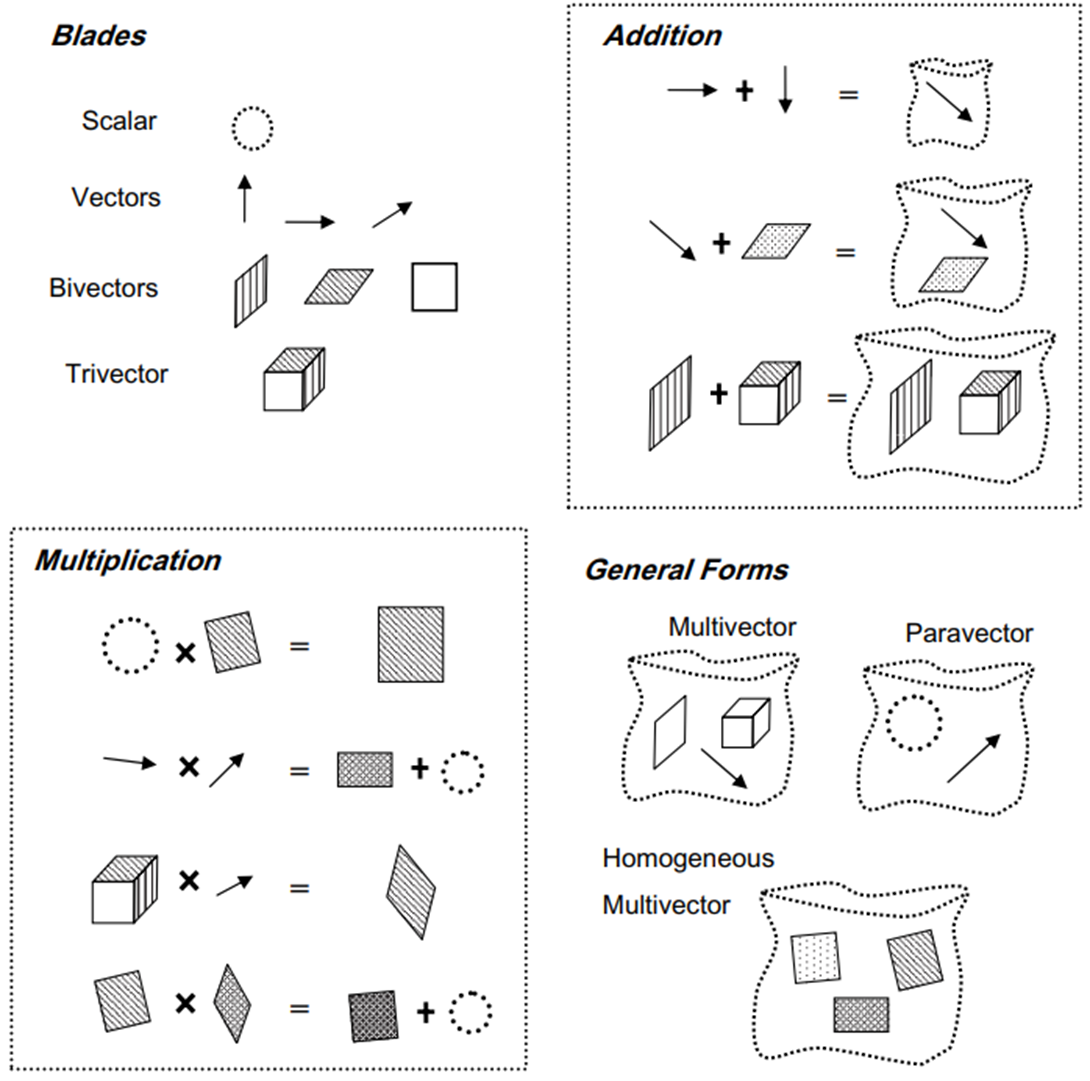
另一個是幾何角度，下圖提供簡單的圖示。

  • Scalar 基本代表 scale or magnitude；vector 則有 vector scale 和 vector 方向；Bi-vector 的大小是面積也有方向 (是面積的方向，不是 normal 的方向)；Tri-vector 的大小是體積，沒有方向?
  • GA 的加法就是同一類的 component 可以相加，不同類 component 互不干涉。
  • GA 的乘法前兩類已經討論過。比較特別的是 trivector 乘 vector 得到 bivector; bivector 乘 bivector 得到 bivector 加上 scalar? Yes.

image-20221204191713985

GA in 1D Geometry (2D Algebra Space Including Imaginary Part)

  • trivia case, only scalar+pseudo-scalar ($i$): $a+bi$, dimension of 2.

  • $i$ 的意義就是旋轉 90 度 in the complex plan (not in the geometry!!) \(\begin{gathered}\text{(scalar+pseudo-scalar)(scalar+pseudo-scalar)}\quad(a+b i)(c+d i)=(a c-b d)+(a d+b c) i \end{gathered}\)

  • 結果仍然是 scalar + pseudo-scalar, 沒有什麽 surprise.

GA in 2D Geometry (4D Algebra Space Including Imaginary Part)

  • Vector: $\vec{u} = a \hat{x} + b \hat{y}$
  • In general: $V = a + b \hat{x} + c \hat{y} + d \hat{x}\hat{y}$

  • 更重要 bi-vector (also 2D pseudo-scalar): $i = \hat{x}\hat{y}$. 2D $i$ 幾何意義就是旋轉 90 度 in the 2D geometry。

    • Example: $\vec{v} = 2 \hat{x} + 3 \hat{y} \to \vec{v} i = 2 \hat{x}\hat{x}\hat{y} + 3 \hat{y}\hat{x}\hat{y} = -3 \hat{x} + 2 \hat{y} $, 逆時針轉 90 度

    • Example: $\vec{v} = 2 \hat{x} + 3 \hat{y} \to i \vec{v} = 2 \hat{x}\hat{y}\hat{x} + 3 \hat{x}\hat{y}\hat{y} = 3 \hat{x} - 2 \hat{y} $, 順時針轉 90 度

\[\begin{gathered} \text{(vector)(vector)}\quad(a \hat{x}+b \hat{y})(c \hat{x}+d \hat{y})=(a c+b d)+(a d-b c) i \\ \text{(scalar+bi-vector)(scalar+bi-vector)}\quad(a+b i)(c+d i)=(a c-b d)+(a d+b c) i \\ \text{(vector)(scalar+bi-vector)}\quad(a \hat{x}+b \hat{y})(c+d i)=(a c-b d) \hat{x}+(a d+b c) \hat{y} \end{gathered}\] \[\vec{v} z=z^* \vec{v} \quad \text{ e.g. } i \vec{v} = -\vec{v} i\\ \vec{v} e^{-i \theta} = e^{i \theta} \vec{v} \\ \vec{u} \vec{v} \vec{w}=\vec{w} \vec{v} \vec{u}\]
  • (vector) (vector) = scalar (inner product) + bi-vector (outer product)
  • (bivector) (bivector) = scalar; 2D bivector 其實就是 (pseudo)-scalar.

  • (vector) (scalar + bivector) = vector

  • 所以 $V = a + b \hat{x} + c \hat{y} + d i$, i.e. scalar+pseudo-scalar (2), vector (2): dimension of 4.

GA in 3D Geometry (8D Algebra Space Including Imaginary Part)

  • Vector: $\vec{u} = a \hat{x} + b \hat{y} + c\hat{z}$

  • In general:

    • 2D multivector: $a + b \hat{x} + c \hat{y} + d \hat{x}\hat{y}$
    • 3D multivector: $a + b \hat{x} + c \hat{y} + d \hat{z} + e \hat{x}\hat{y} + f \hat{y}\hat{z} + g \hat{x}\hat{z} + h \hat{x}\hat{y}\hat{z}$

  • 更重要 tri-vector (also 3D pseudo-scalar): $i = \hat{x}\hat{y}\hat{z}$. 3D $i$ 幾何意義“不是”旋轉 90 度. $A i = iA$

    • Example: $\vec{v} = \hat{x} \to \vec{x} i = \hat{x}\hat{x}\hat{y}\hat{z} = \hat{y} \hat{z} $: vector 乘 $i$ 變成 bi-vector, 方向 follow 右手性。(或是從平面變成 normal vector)

    • Example: $\vec{v} = \hat{x}\to i \vec{x} = \hat{x}\hat{y}\hat{z}\hat{x} = \hat{y}\hat{z}$: 同樣結論。

    • Example: $i \hat{y}\hat{z} = \hat{x}\hat{y}\hat{z}\hat{y}\hat{z} = -\hat{x}$: bi-vector 乘 $i$ 變成 vector, 方向 follow 左手性。

    • 所以在 3D (NOT 2D!), 可以用 $i$ 互換 cross product and outer product

      • $\vec{u}\times\vec{v} = i \vec{u}\wedge\vec{v} = \vec{u}\wedge\vec{v} i$
      • 3D 的旋轉 $T$ 度比較複雜！ ： $e^{\hat{x}\hat{y}\frac{T}{8}} \vec{v} e^{\hat{x}\hat{y}\frac{T}{8}}$
  • 所以 $V = a + b \hat{x} + c \hat{y} + d \hat{z} + e i \hat{z} + f i \hat{x} + g i \hat{y} + h i $, i.e. scalar+pseudo-scalar (2), vector (3), pseudo-vector (3): dimension of 8.
  • (vector) (vector) = scalar (inner product) + bi-vector (outer product)
    • $(a \hat{x}+b \hat{y} + c\hat{z})(d \hat{x}+e \hat{y} + f\hat{z})=(a d+b e + cf)+(ae-bd)\hat{x}\hat{y}+(bf-ce)\hat{y}\hat{z}+(af-cd)\hat{x}\hat{z} $
  • (bivector) (bivector) = scalar (bivector inner product) + bi-vector (outer product)
    • $(a\hat{x}\hat{y}+b\hat{y}\hat{z}+c\hat{z}\hat{x})(d\hat{x}\hat{y}+e\hat{y}\hat{z}+f\hat{z}\hat{x})=-(a d+b e + cf)+(ae-bd)\hat{x}\hat{z}+(bf-ce)\hat{y}\hat{x}+(af-cd)\hat{y}\hat{z} $
  • (vector) (bivector) = (psedu)-scalar + vector
    • $(a \hat{x}+b \hat{y} + c\hat{z})(d\hat{y}\hat{z}+e\hat{z}\hat{x}+f\hat{x}\hat{y})=i(a d+b e + cf)+(ce-bf)\hat{x}+(af-dc)\hat{y}+(bd-ae)\hat{z} $

GA in 4D Geometry (16D Algebra Space Including Imaginary Part?)

  • Vector: $\vec{u} = a \hat{x} + b \hat{y} + c\hat{z} + d\hat{t}$
  • 4D multivector: $V = a + b \hat{x} + c \hat{y} + d \hat{z} + e \hat{t} + f \hat{x}\hat{y} + g \hat{y}\hat{z} + h \hat{z}\hat{t} + k \hat{x}\hat{z} + l \hat{x}\hat{t} + m\hat{y}\hat{t} + n \hat{x}\hat{y}\hat{z} + o \hat{x}\hat{y}\hat{t} + p \hat{t}\hat{y}\hat{z} + q \hat{x}\hat{z}\hat{t} + r \hat{x}\hat{y}\hat{z}\hat{t}$
  • $V = a + b \hat{x} + c \hat{y} + d \hat{z} + e \hat{t} + f \hat{x}\hat{y} + g \hat{y}\hat{z} + h \hat{z}\hat{t} + k \hat{x}\hat{z} + l \hat{x}\hat{t} + m\hat{y}\hat{t} + ni \hat{x} + o i\hat{y} + p i\hat{z} + q i\hat{t} + r i$, i.e. scalar+pseudo-scalar (2), vector (4), pseudo-vector (4), Bivector (6): dimension of 16.
  • 4D: (vector) (vector) = scalar (inner product) + bi-vector (outer product)
  • 但是 (bivector) (bivector) 不是 inner + outer!

GA Eigenvalue and Eigenvector

既然提到 vector, 自然就會聯想到 vector space, linear algebra, linear transformation, matrix multiplication, eigenvalue, eigenvector.

簡單 review vector space 和 linear transformation

  • 假設 $f$ 是 linear transformation on a vector space, 可以被 extending linear transformation (outer morphism)
    • Definition: $f(u\wedge v) = f(u)\wedge f(v)$
    • Definition: $f(a\wedge b + c\wedge d) = f(u)\wedge f(v) + f(c)\wedge f(d)$
    • Definition: $f(u\wedge v\wedge w) = f(u)\wedge f(v)\wedge f(w)$
  • Eigenvector and eigenvalue: linear transformation 仍然維持原來的方向！ scaling factor 就是 eigenvalue
  • Eigen-trivector and eigen-trivalue: 因爲 tri-vector 沒有方向 (only + or -), 所以一定是 eigen-trivector! eigen trivalue $\lambda$ 就是 determinant!!!
    • $f(u\wedge v\wedge w) = f(u)\wedge f(v)\wedge f(w) = \lambda (u\wedge v\wedge w)$
  • Eigen bivector and eigen bivalues: 就是 preserve bi-vector 的方向 (rotation!) rotation angles 就是 eigen bivalue?！！
    • $f(u\wedge v) = \lambda f(u)\wedge f(v) = \lambda (u\wedge v)$ where $\lambda = \alpha^2 + \beta^2$ 是一個 real value
    • 這是什麽意思，就是兩個 vectors 經過 linear transformation, 仍然落在同一個平面上！！！！ （但是不需要同一個方向！！！）
    • 但是 2D 不全部都落在同一個平面？ 需要保角度嗎 (conformal?) 。2D 的 i 代表 e1 e2, 就是轉 90 度
    • 3D 的i 代表 e1 e2 e3 ， 代表落在 2D 平面就 ok??

###

3D linear transformation 的 eigenvalue and eigenvectors

  1. vector: preserved vector 方向: value scaling factor : eigenvector and real value eigenvalue: 長度的 ratio
  2. bivector: scaled rotation 方向: eigen bivector and complex eigen value: (面積的 ratio?)
  3. trivector: volume ratio!
  Real eigenvector Real eigenvalue Complex eigenvector Complex eigenvalue
2D real matrix Preserve vector 方向 Vector 長度 ratio    
2D complex matrix Preserve ?      
3D real matrix Preserve vector 方向 Vector 長度 ratio Preserve bivector 方向 Bivector 面積 ratio
conjugate?
3D complex matrix        
4D real matrix Preserve vector 方向 Vector 長度 ratio Preserve bivector 方向 Bivector 面積 ratio
4D complex matrix        

2D

Given a 2D real linear transformation A, 可以分解成兩類

  • Real eigenvalue: $A = Q D Q^{-1}$, D 是 diagonal matrix with 2 real eigenvalues. Q 的 2 個 column vectors 對應兩個 real eigenvectors. A 就是旋轉, scale, 再反旋轉？ eigenvector preserve 方向，只有 scale.
  • 如果 A 是對稱矩陣，Q = Q-1 and 2 個 column eigen-vectors 是正交 vectors!! 但如果 A 不是對稱矩陣，則 Q =~ Q! and eigen-vector 非正交!!
  • Complex eigenvalue: $A = [\cos\theta, -\sin\theta; \sin\theta, \cos\theta]$ 代表逆時針旋轉 $\theta$ 度。D 是 diagonal matrix with $\exp(\pm i \theta)$ eigenvalues. $Q = = [\cos\frac{\theta}{2}, -\sin\frac{\theta}{2}; \sin\frac{\theta}{2}, \cos\frac{\theta}{2}]$ 此時應該用 bivector 來看. $A (u\wedge v) = A u \wedge A v = \lambda (u\wedge v)$ and $\lambda=1$ 是實數。在 2D $u\wedge v$ 的大小就是 $u$ and $v$ vector 包出的面積。沒有方向因為都是 pseudo-scalar (i). 也就是保面積的 linear transformation, 就是旋轉。
  Eigenvalue Real Eigen (vec/bivec/trivec) Complex eigenvector
Vector Real if vector preserve 方向
$i$ if it’s a rotation matrix with $\theta$
$\alpha+\beta i$ if it’s scaled rotor		 Vector 長度 ratio  
Bi-vector
pseudo-scalar, $i$		 1 if it’s a rotation matrix with $\theta$
$\alpha^2+\beta^2$ if it’s scaled rotor		 area ratio is 1  
Tri-vector det(A) ratio of volume always real (only +/-)

2D, 1 or 2 互斥 (scale or scaled rotation)

  1. 一定存在: 面積的比

image-20221212230147937

3D, 1 一定存在可能是 1 or 3 個方向

3D, 2 不一定存在，如果是旋轉坐標就存在 ; complex eigenvalue

3 永遠存在 (但 eigen trivector, i.e. determiant 可能為 0)

Spacetime Physics with Geometric Algebra1

Ray tracing: Geometric Algebra for Computer Science

SLAM: Geometric Algebra Applications Vol. I Computer Vision, Graphics and Neurocomputing

NeRF?/NAF

Medical image

Applications

Spacetime Physics with Geometric Algebra1

Ray tracing: Geometric Algebra for Computer Science

SLAM: Geometric Algebra Applications Vol. I Computer Vision, Graphics and Neurocomputing

NeRF?/NAF

Medical image

Machine learning?

Machine Learning

GA 的 scalar 是 cosine similarity; bivector 是 sine area.

可以用來取代 cosine similarity 嗎?

Application in Physics

Maxwell Equation

首先定義: \(\begin{aligned} \nabla &=\frac{1}{c} \frac{\partial}{\partial t}+\vec{\nabla} \\ \vec{\nabla}&= \frac{\partial}{\partial x} \hat{x}+\frac{\partial}{\partial y} \hat{y}+\frac{\partial}{\partial z} \hat{z} \\ J &=c \rho-\vec{J} \\ F &=\vec{E}+i c \vec{B} \\ \end{aligned}\)

  • $\vec{B}$ is bivector, $i$ 是 trivector, 所以 $i \vec{B}$ 變成 vector 可以和 $\vec{E}$ 一致
  • $\rho$ 是 scalar, $\vec{J}$ 是 vector.
  • Caveat: $\nabla F = \nabla \cdot F + \nabla \wedge F$

Maxwell Equation 可以簡化成: \(\begin{aligned} &\text{Maxwell Equation: } \nabla F = \frac{J}{c \varepsilon_0} \\ \Rightarrow &\left(\frac{1}{c} \frac{\partial}{\partial t}+\vec{\nabla}\right)(\vec{E}+i c \vec{B})=\frac{c \rho-\vec{J}}{c \varepsilon_0}\\ & \vec{\nabla} \cdot \vec{E}+\frac{1}{c} \frac{\partial \vec{E}}{\partial t}+i c \vec{\nabla} \wedge \vec{B}+\vec{\nabla} \wedge \vec{E}+i \frac{\partial \vec{B}}{\partial t}+i c \vec{\nabla} \cdot \vec{B}=\frac{\rho}{\varepsilon_0}-\frac{\vec{J}}{c \varepsilon_0} \\ \Rightarrow & \text{ (scalar, Gauss Law) }\vec{\nabla} \cdot \vec{E}=\frac{\rho}{\varepsilon_0} \\ & \text{ (vector, Ampere Law) } \frac{1}{c} \frac{\partial \vec{E}}{\partial t}+i c \vec{\nabla} \wedge \vec{B}=-\frac{\vec{J}}{c \varepsilon_0} \longrightarrow \vec{\nabla} \times \vec{B} - \mu_0 \varepsilon_0 \frac{\partial \vec{E}}{\partial t} =\mu_0 \vec{J} \\ & \text{ (bivector, Faraday Law) } \vec{\nabla} \wedge \vec{E}+i \frac{\partial \vec{B}}{\partial t}=0 \longrightarrow \vec{\nabla} \times \vec{E}+ \frac{\partial \vec{B}}{\partial t}=0\\ & \text{ (trivector) } i c \vec{\nabla} \cdot \vec{B}=0 \longrightarrow \vec{\nabla} \cdot \vec{B}=0 \\ \end{aligned}\)

Rotor and Spinor

GA 的缺點

似乎很明顯，

  • 就是 dimension 太多： 2D 還好，只有 4 dimension: 1 (scalar) + 2 (vectors) + 1 (bivector, scalar)

3D 需要 8 dimension: 1 (scalar) + 3 (vectors) + 3 (bivector) + 1 (trivector, scalar)

= 8. 如果 4D 需要 16 dimension.

  • How to reconcile the $i$ difference between 2D and 3D? No problem at all, 2D 的 $i$ 就是 $\hat{e}_1 \hat{e}_2 = - \hat{e}_2 \hat{e}_1 \to (\hat{e}_1 \hat{e}_2)^2 = \hat{e}_1 \hat{e}_2 \hat{e}_1 \hat{e}_2 = - \hat{e}_1 \hat{e}_2 \hat{e}_2 \hat{e}_1 = -1$

  • 3D 的 $i = e_1 e_2 e_3$ = $(\hat{e}_1 \hat{e}_2 \hat{e}_3)^2 = \hat{e}_1 \hat{e}_2 \hat{e}_3 \hat{e}_1 \hat{e}_2 \hat{e}_3 = - \hat{e}_1 \hat{e}_2 \hat{e}_3 \hat{e}_1 \hat{e}_3 \hat{e}_2 = \hat{e}_1 \hat{e}_2 \hat{e}_3 \hat{e}_3 \hat{e}_1 \hat{e}_2 = (\hat{e}_1 \hat{e}_2)^2 = -1$

Citation

Geometric Algebra: very good!!!

https://www.youtube.com/watch?v=60z_hpEAtD8&ab_channel=sudgylacmoe

Tensor Calculus: MathTheBeautiful

3D case of Geometric algebra?

https://www.youtube.com/watch?v=e0eJXttPRZI&ab_channel=MathTheBeautiful

Covariance and Contra-variance of vector/tensor?

Unify covariance and contra-vairance of vector/tensor??

in Allen Lu MWEB: 相對論和張量分析 - Coordinate Covariant, Contravariant, Invariant (座標系協變，逆變，不變)

1-form and ? -form tensor calculus?

In Allen Poincaré conjecture/theorem and Ricci flow

Tensor calculus: Allen Lu MWEB: and Youtube maththebeautifu!!

https://www.youtube.com/watch?v=e0eJXttPRZI&ab_channel=MathTheBeautiful

Poincare Conjecture/Theorem and Ricci Flow

Differential geometry vs. Tensor Analysis vs. Geometric Algebra

Differential geomery base: 1. 座標無關，2. 曲面，3. Einstein symbol (covariant and contra variant == vector and 1-form???)

Tensor analysis: 1. 座標無關，2. 平面(?)，3. Einstein symbol (vector and 1-form)

Geometric Algebra: 1. tightly coupled with 座標? 2. 平面 (no)?

我們從問題出發

  1. Tensor analysis/calculus 和 geometric algebra, 到底誰 cover 誰?
  2. Tensor 的基礎是座標不變性。在 geometric algebra 對應是什麼?
  3. Covariant and Contravariant 對應 geometric algebra 什麼?
  4. vector vs. 1-form, vector 對應 geometric algebra 的 2D, 1-form 對應什麼?
  5. Einstein symbol 在 geometric algebra 有表現嗎?
  6. 目前都是平面，在曲面或是 manifold, 那一個更 general?
  7. Manifold 也有 geometric algebra 嗎? exp map and tagent plane 有對應的表現嗎?
  8. Maxwell queation in different forms. General relativity in different forms!

(4) David Hestenes - Tutorial on Geometric Calculus - YouTube

image-20221202225211143