Reference
LCF: Eigenvector 的 2D 幾何物理意義 (lcf0929.blogspot.com)
Summary (Reference 2)
- 特征向量 (Eigenvector)描述的是矩阵的方向不变作用(invariant action)的向量;
- 奇异向量 (Single vector) 描述的是矩阵最大作用(maximum action)的方向向量。
- 除非是 symmetric matrix, eigenvectors 不會正交。
- Single vector 則是強迫正交
- 所以 ED 和 SVD 一樣是在 symmetric matrix.
Introduction
Reference 1 寫的非常好,直接引用。
eigenvalue / eigenvector 相較於線性轉換或座標轉換而言, 其物理意義是較為抽象且不同應用有不同的物理意義。剛好 2D 比較容易用幾何意義説明。
$A x = \lambda x$ 此處 $\lambda$ 是實數而非複數 (real not complex number)!
白話來說, 就是一個線性轉換, 可能會存在一向量, 該向量經過該線性轉換得到的結果只有縮放, 沒有旋轉. 該向量即為 eigenvector, 而縮放的大小, 就是 eigenvalue (real value).
- 注意此處 0 vector 仍然轉換成 0 vector, 沒有 bias.
- 如果有 bias, 可以轉換成 3D, (x, y, z) -> (x, y, 1), 稱爲 homogenous (TBA)
向量的移動
在看特徵向量之前, 先了解2維向量經過一矩陣線性轉換後, 對圖形會有什麼變化 這個轉換我們可以想像成一股力量迫使原本的向量改變的他們的位置移動到新的位置上 2x2 矩陣的移動可以簡單的想像是由四種基本力量結合在一起所產生, 分別為
- 水平軸的水平力量 (張力)
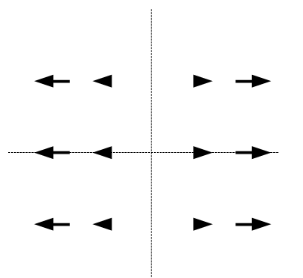
當為正能量, 該力量在 x > 0 往右拉, 在 x < 0 往左拉, 力量成線性變化, 也就是該力量越往在 x = 0 (y 軸上) 會越小, 當再 x = 0 時會沒有這股力量, 可參考上圖。
- 水平軸的垂直力量 (剪力)
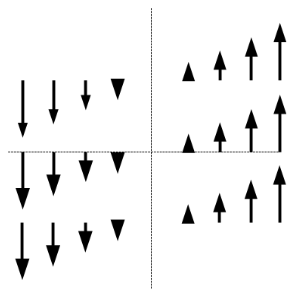
當為正能量, 該力量在 x > 0 往上, 在 x < 0 往下, 力量成線性變化, 也就是該力量越往在 x = 0 (y 軸上) 會越小, 當再 x = 0 時會沒有這股力量, 可參考上圖
- 垂直軸的垂直力量 (張力)
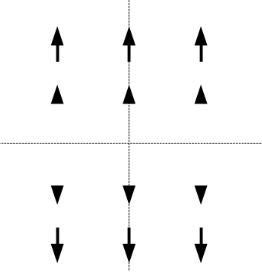
當為正能量, 該力量在 y > 0 往上拉, 在 y < 0 往下拉, 力量成線性變化, 也就是該力量越往在 y = 0 (x 軸上) 會越小, 當再 y = 0 時會沒有這股力量, 可參考上圖
當為負能量, 該力量在 y > 0 往下推, 在 y < 0 往上推, 也就是正能量箭頭反向後的結果.
-
垂直軸的水平力量 (剪力)
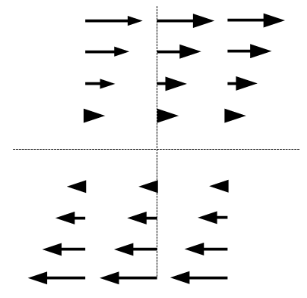
當為正能量, 該力量在 y > 0 往右, 在 y < 0 往左, 力量成線性變化, 也就是該力量越往在 y = 0 (x 軸上) 會越小, 當再 y = 0 時會沒有這股力量, 可參考上圖
當為負能量, 該力量在 y > 0 往左, 在 y < 0 往右, 也就是正能量箭頭反向後的結果.
其實該力量用2維陣列表示就是長這個樣子
水平軸的水平張力 垂直軸的水平剪力 水平軸的垂直剪力 垂直軸的垂直張力
了解力量的特性後, 還有一個假設, 我們要假設原點有股力量會將分布在座標上的點往圓心方向拉, 該力量為
\[\left[\begin{array} {cc}-1 & 0\\0 & -1\end{array}\right]\]因此, 當要維持目前座標上所有點的位置, 需要有一股基本力量來維持, 也就是
\[\left[\begin{array} {cc}1 & 0\\0 & 1\end{array}\right]\]因此移動向量會是施與的力量減去往原點的力量, 施予力量
\[\left[\begin{array} {cc}a & c\\b & d\end{array}\right]\]其移動力量為
\[\left[\begin{array} {cc}a-1 & c\\b & d-1\end{array}\right]\]因此, 當矩陣為基本的力量時, 移動向量會是 0 (矩陣向量不變).
2D 變換基本行為
所有的2維線性轉換向量移動方式, 皆由上面四大基本力量所組成。
幾何詮釋:所有 2x2 線性變換, 其整體行為可以分成兩大類
- 無整體旋轉行為
- 有整體旋轉行為
代數詮釋:eigenvalue and eigenvector
Eigenvalue 和 eigenvector 加入作爲代數的判斷,定義如下: \(\left[\begin{array} {cc}a_{11} & a_{12}\\a_{21} & a_{22}\end{array}\right] \left[\begin{array} {cc}v_{1} \\v_{2}\end{array}\right]= \lambda \left[\begin{array} {cc}v_{1} \\v_{2}\end{array}\right]\)
\[(a_{11}-\lambda)(a_{22}-\lambda) - a_{21}a_{12} = 0 \\ \lambda^2 - (a_{11}+a_{22})\lambda + (a_{11} a_{22}-a_{12}a_{21}) = 0 \\ \lambda = \frac{a_{11}+a_{22}\pm \sqrt{(a_{11}+a_{22})^2-4(a_{11} a_{22}-a_{12}a_{21})}}{2} \\ \lambda = \frac{a_{11}+a_{22}\pm \sqrt{(a_{11}-a_{22})^2+4 a_{12}a_{21}}}{2}\]所有 2x2 線性變換, 可以分爲
- 實數 (real number) 的 eigenvalues and eigenvectors 代表有兩個不動 (invariant) 的 ”主軸“ (eigenvectors)。
- Eigenvalue decomposition: $A = Q D Q^{-1}$, 此處 $D$ 是 diagonal matrix of eigenvalues.
- 如果 $A$ 是 symmetric matrix: real eigenvalues and real eigenvectors. 並且 $Q^{-1} = Q^{T}$ 是 orthogonal matrix.
- 複數 (complex number) 的 eigenvalues and eigenvectors 代表沒有不動的主軸,而是一個旋轉軸 (bi-vector)。
Ex1: 線性轉換矩陣
\[A = \left[\begin{array} {cc}2 & 1\\1 & 2\end{array}\right] = \left[\begin{array} {cc}1 & 0\\0 & 1\end{array}\right] + \left[\begin{array} {cc}1 & 1\\1 & 1\end{array}\right]\]-
Eigenvalues: 1 and 3.
-
Eigenvectors: $\frac{1}{\sqrt{2}}[\pm 1,1]$ 如下圖藍色方向。注意 $A$ 是 symmetric matrix, eigenvectors 正交。
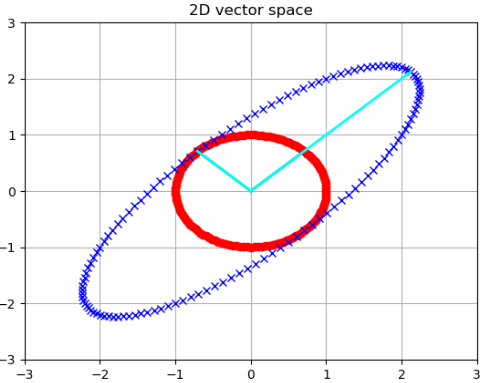
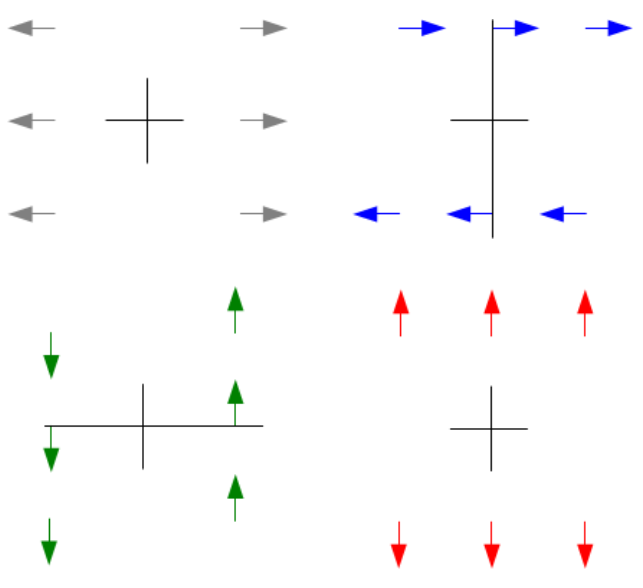
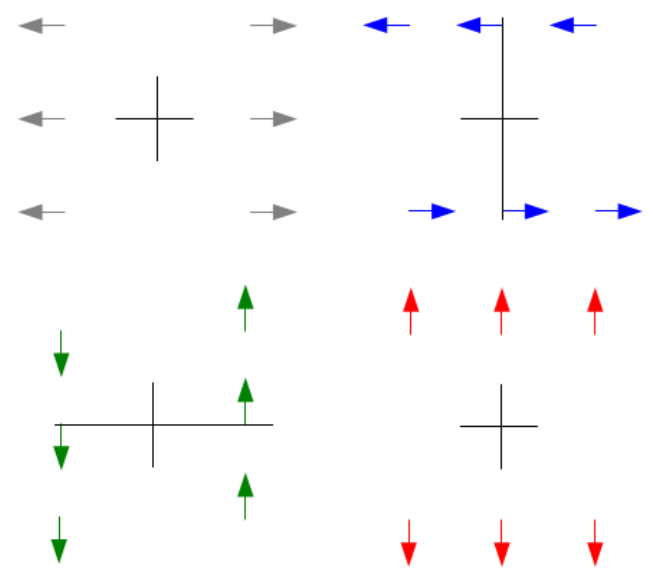
其移動向量為 \(\left[\begin{array} {cc}1 & 1\\1 & 1\end{array}\right]\) 四個基本移動向量對應到九個位置如下圖
(-1, 1), (0, 1), (1, 1), (-1, 0), (0, 0), (1, 0), (-1, -1), (0, -1), (1, -1)
用圖形表示該矩陣
- 左上灰色為水平軸的水平移動量 (張力)
- 右上藍色為垂直軸的水平移動量 (剪力)
- 左下綠色為水平軸的垂直移動量 (剪力)
- 右下紅色為垂直軸的垂直移動量 (張力)
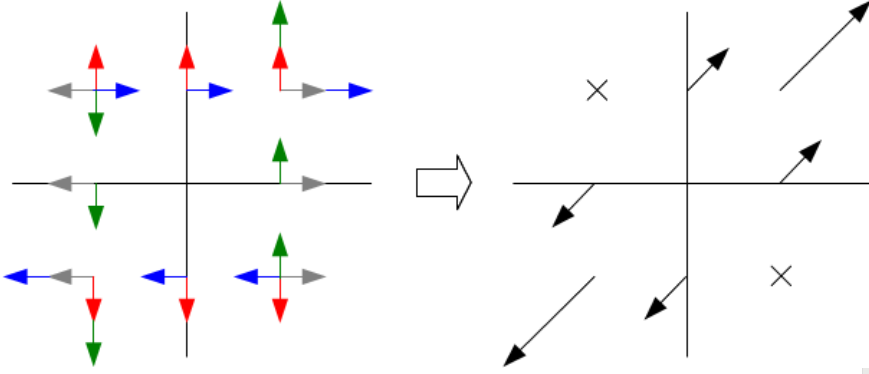
相加後
- 藍色的順時針剪力和綠色的逆時針剪力抵消旋轉的力量。
- 紅色和灰色的張力合成向外的張力。
- 最後得到 45 (-135) 度方向的張力和 135 (-45) 度方向的推力。也就是 eigenvectors 的方向。大的 eigenvalue (3) 對應 45 (-135) 度方向。小的 eigenvalue (1) 對應 -45 (+135) 度方向。
- 因爲 A 是對稱矩陣,可以證明 eigenvectors 是正交。
旋轉的幾何詮釋
所謂的旋轉是該點會有一股位移力量, 該力量可分解為該點至圓心的線, 與垂直於該線之方向, 垂直於該線之方向若移動的力量非零,則對該點產生旋轉, 如果每個點相對的旋轉方向(順時針或逆時針) 皆相同, 那麼就有整體旋轉的行為存在, 否則只有個體旋轉的情形無整體旋轉之行為.
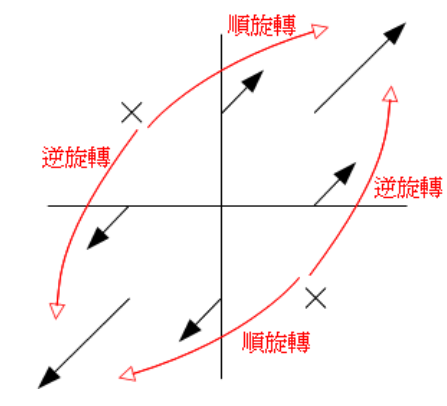
因為變化為線性, 無整體旋轉行為在旋轉方向是區段不同的, 在兩個不同的旋轉方向之間, 必定存在至少一個向量旋轉能量為 0, 而不會旋轉的向量, 就是所謂的特徵向量
旋轉的幾何的必要 (但非充分) 條件就是剪力不能抵消:$a_{12} a_{21} < 0$. 這和代數的條件一致。
Ex2: 旋轉的例子:
\[\left[ \begin{array} {cc} 2 & -1\\ 1 & 2 \end{array} \right]\]- Eigenvalues: $2\pm i$.
- Eigenvectors: $\exp(\pm i\pi/8)$
最後的移動量為
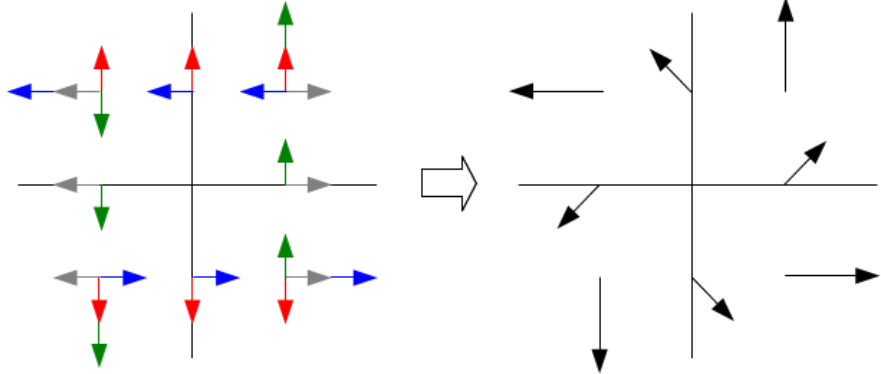
可以看出, 所有點都具有逆時針旋轉的移動方向, 故不會存在任一位置向量不具旋轉特性, 這種矩陣, 因不存在不具旋轉特性的向量, 即無實數的特徵向量。但有特徵 bi-vector!
Ex3: Rotation Matrix
\[A= \left[ \begin{array} {cc} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{array} \right]\]-
Eigenvalues: $\cos\theta \pm i \sin\theta = \exp(\pm i \theta)$
-
Eigenvectors: $[1, \pm i]$.
-
複數的 eigenvalues 和 eigenvectors 有幾何意義嗎? 我們可以猜測是旋轉,但是無法直觀理解。
2D Linear Transform Summary
如何判斷 2x2 線性變換 A 有無整體旋轉行為? 用張力剪力 (幾何) 以及 eigenvalue and eigenvector (代數) 判斷:
- A 無整體旋轉行為 :
- 幾何:剪力反向 (一個順時針,一個逆時針), i.e. $a_{12} a_{21} > 0$
- 代數:real eigenvalues and eigenvectors, 和幾何一致。
- A 有整體旋轉行為 :
-
幾何: 剪力同向 (都是順時針或是逆時針), i.e. $a_{12} a_{21} < 0$, 並且剪力平均值大於張力净值, i.e. $\sqrt{ a_{12}a_{21} }> a_{11} - a_{22} /2$. - 代數:complex eigenvalues and eigenvectors: $(a_{11}-a_{22})^2 + 4 a_{12} a_{21} <0$, 和幾何一致。
-
- A 是 symmetric matrix:
- 幾何解釋:藍綠剪力反向,旋轉的力道對消,不會旋轉。
- 代數解釋:symmetric matrix $a_{12} a_{21} > 0$. 根號判別式一定為正:real eigenvalues and eigenvectors.
- 注意:symmetric matrix 的 eigenvectors 正交!
- A 是 rotation matrix:
- 幾何解釋:藍和綠同爲逆時針旋轉。
- 代數解釋: $a_{12} a_{21} < 0$ and $a_{11}-a_{22} = 0$. 根號判別式為負。所以是 complex eigenvalues and eigenvectors.
單位圓
與其用影像變化的角度來看, 用單位圓的變化來看會更直接, 因為單位圓有個特色就是從圓心到圓上的所有向量大小都為 1,單位圓的線性變化, 會實實在在的反應出該線性轉換帶給各角度向量旋轉與縮放的力道.
單位圓經過線性轉換是什麼變化, 其實就是從圓, 變成(斜)橢圓
因此, 我們可以從單位圓, 跟橢圓之間向量方向的變化, 來找出當相同(或相反)方向時的向量, 即為特徵向量 (eigen-vectors).
假設單位元經過線性轉換如下 \(A = \left[ \begin{array} {cc} 1 & 0.5\\ 0.3 & 1 \end{array} \right]\)
- Eigenvalues: 0.6127 and 1.3873.
- Eigenvectors: $[\pm 0.79057, 0.61237]$. 因爲 $A$ 不是 symmetric matrix, 所以 eigenvectors 並非正交。

Geometric Algebra Bivector: “Eigenvalue” and “Eigen-bivector”
- Geometric Algebra 用 bi-vector 提供直觀的理解。
- Bi-vector 是兩個 vectors 的 wedge product (NOT geometric product, 因為 geometric product 包含 scalar and bi-vector). 在 2D plan bi-vector 是 pseudo-scalar 只有大小,沒有方向 (最多正負號) 或者方向就是 2D plane。大小就是兩個 vectors 夾出的面積。如果這兩個 vectors 是 basis vectors ($e_1$ and $e_2$), wedge product 就等於 geometric product.
- 如何定義 bi-vector 的 linear transformation? 就是定義兩個 vectors 各自的 linear transformed vectors 的 wedge product (Again, NOT geometric product). 以 rotation matrix (linear transformation) 爲例:
- 注意 rotation matrix (linear transformation) 沒有實數的 eigenvalues (for vector) 和 eigen-vectors.
- 但從上式看出 rotation matrix 有實數的 eigen-value for bi-vector, eigenvalue 是 (real number) 1; eigen-bivector 是 $e_1\wedge e_2$: 幾何意義:Eigen-value 的大小代表 eigen-bivector linear transformation 的面積比 (1 in this case). 在 2D bivector 沒有方向或就是 2D 平面本身。注意 eigen-value 1 剛好是 $A$ 的 determinant. 這有廣汎性嗎? Yes.
- 任意 2D matrix 是否 basis bi-vector $(e_1\wedge e_2)$ 也是 eigen-bivector? Yes! eigenvalue 就是 (real) determinant!
- Yes. 在 3D and above eigen-bivector 有 preserve bivector 方向
- 任意 2D matrix 是否任意 bi-vector of $(v_1\wedge v_2)$ 也是 eigen-bivector? Yes!
- 如下,雖然 eigen-vectors 是任意 2 vectors,但是 eigenvalue 唯一,就是 (real) determinant!
-
如果任意 bi-vector 都是 eigen-bivector in 2D and preserve 方向和大小, 所謂 (rotation matrix) eigen-bivector 有任何意義嗎?
- Yes. 在 3D space and above bivector 是有方向性的。eigen bivector 則是 preserve bivector 方向,也就是和 linear transformation 和 bivector 同一平面的 bi-vector.
2D Linear Transformation w/ Real A: Eigen-bivectors and Eigenvalues
所有 bivector 在 2D linear transformation (不論是旋轉或是非旋轉) 都是 eigen-bivector with eigenvalue det(A).
- 所以旋不旋轉對於 2D bivector 好像沒有什麽意義。
- 但是在 3D or above 空間 bivector 有方向。 Eigen-bivector 代表 linear transformation 后仍然 preserve bivector 方向。就像 Eigen-vector 代表 linear transformation 仍然 preserve vector 方向。
- 在任何 dimension (2D, 3D, or above) 的 real eigenvectors 所形成的 bivectors 都是 eigen-bivectors.
- 2D: real eigenvectors 形成的 bivector 也是 eigen-bivectors. 假設 $v_1$ and $v_2$ 是 real eigenvectors with $\lambda_1$ and $\lambda_2$ eigenvalues.
-
2D: complex eigenvector, 可以得到 real eigenvalue!
\(A (v_1 \wedge v_2) = A v_1 \wedge A v_2 = \det(A) (v_1 \wedge v_2)\) -
2D: 如果是 real matrix A, 可以證明即使是 complex eigenvalues, 也是 conjugate! 也就是 $\lambda_2^* = \lambda_1$, or $a\pm b i$. 所以 $\lambda_1 \lambda_2 = a^2 + b^2 \in \mathbf{R}$. 所以 eq (17) 和 eq (18) 其實等價。
- Real A, real eigenvalues $\lambda_1, \lambda_2$ :
- Real A, complex conjugate eigenvalues $\lambda_1, \lambda_1^*$ : \(A (v_1 \wedge v_2) = A v_1 \wedge A v_2 = \lambda_1 v_1 \wedge \lambda_1^* v_2 = \lambda_1 \lambda_1^* (v_1 \wedge v_2) = \|\lambda_1\|^2 (v_1 \wedge v_2) = \det(A) (v_1 \wedge v_2)\)
-
對於 2D matrix A, 不管旋轉或不旋轉,所有的 bivector 都是 eigen-bivector, 對應 real-eigenvalues, det (A)!
-
這樣好像 eigen-bivector 沒有什麽重要意義,除了對應 eigenvalue 都是 det(A). 並不完全如此,eigen-bivector 在 3D and above 有意義,因爲有方向。
3D Linear Transformation w/ Real A: Eigen-bivectors and Eigenvalues
根據 linear algebra, 只有兩種情況 (不考慮 degenerate cases):
-
3 real eigenvalues and eigenvectors ($\lambda_1, v_1; \lambda_2, v_2; \lambda_3, v_3$)
-
三個 eigenvectors 中任意兩個 eigenvectors 組成的 bivector 在 linear transformation 之後仍然是同一個平面的 bivector! 也就是 eigen-bivector, 對應的 eigenvalue 是 $\lambda_i \lambda_j$ \(A (v_i \wedge v_j) = A v_i \wedge A v_j = \lambda_i v_i \wedge \lambda_j v_j = \lambda_i \lambda_j (v_i \wedge v_j)\)
-
也就是有三個 eigen-bivectors: $(v_i \wedge v_j)$ where $i,j \in [1,2,3]$, 對應 eigenvalues 是 $\lambda_i \lambda_j$.
-
Conjecture: 這種 case, 有三個 (real) eigenvectors, 以及三個 (real) eigen-bivectors.
-
1 real eigenvalue and 2 conjugate eigenvectors ($\lambda_1, v_1; \lambda_1^, v_1^; \lambda_3, v_3$)
- $v_1 \wedge v_1^$ 對應的 eigenvalue 是 $\lambda_1 \lambda_1^ = |\lambda_1|^2$ real and positive number. 理論上 $v_1 \wedge v_1^*$ 也是 real eigen-bivector, how to compute?
- $v_1 \wedge v_3$ 以及 $v_1^* \wedge v_3$ 對應的 eigenvalues $\lambda_1 \lambda_3$ and $\lambda_1^* \lambda_3$ 都是複數。因此這兩個都不是 real eigen-bivector.
- Conjecture: 這種 case, 只有一個 (real) eigenvector, 以及一個 (real and positive) eigenbivector (平面).
-
3D 任何 tri-vector (不用 eigen-vectors) 都是 real (pseudo-scalar) eigen-trivector, 對應 eigen-value 是 $\det(A)$
3D Linear Transformation 幾何詮釋
任何的 3D linear transformation 可以分解成三個 real eigenvectors. 或是一個 real eigen-vector 加上一個旋轉的 real eigen-bivector.
如何表示一個 3D bivector? i x vector?
And i part
How to link GA to linear algebra transform