Reference
https://zhuanlan.zhihu.com/p/353637184 : 解釋 eigenvalue decomposition and SVD 的差別。
eigs.pdf (mathworks.com) : 數學推導。
tobydriscoll/EigenShow.jl: Interactive demonstrator of eigenvectors and singular vectors (github.com) : EigenShow.jl 圖形顯示 EVD 和 SVD 的差別, very cool!
Introduction
特徵值 (Eigen value) 和奇異值 (Singular value) 是兩個極其重要而又相關的概念,但也常令人困惑,它們各自的本質和差異是什麼?
至少我在學綫性代數搞不清兩者的差別,Reference 給了很好的説明。
最重要結論:
-
特徵向量 (Eigen vector) **描述的是矩陣的方向 (座標系) **不變作用 (invariant action) 的向量;
-
奇異向量 (Single vector) 描述的是矩陣最大作用 (maximum action) 或是保持正交的方向向量。
次結論:
- EVD 的 eigen-vectors 在對稱方陣正交 (或是推廣到複數的 Hermitian matrix)。但在大多數非對稱方陣 eigen-vectors 不會正交!
- SVD 的 singular-vectors 一定正交!
-
對稱方陣的 EVD 和 SVD 在幾何上基本等價。但在數學上有些微差距:Singular-values = Eigen-values 因爲 singular value 要求正實數或零。Eigen value 在對稱方陣一定是實數,但不一定是正實數。
“eigen”在德語中的意思是“own”,“自己的”。特徵值和特徵向量起源於18世紀歐拉和拉格朗日對於旋轉剛體的研究,拉格朗日發現:主軸是剛體慣性矩陣的特徵向量。之後,柯西、傅立葉、拉普拉斯等近多位科學家進行了相關的工作。1904年,希爾伯特(David Hilbert) 在研究積分號的特徵值時,首先使用德語”eigen”和英語的組合:eigenvalues 和 eigenvectors,成為了今天的標準術語。總之,特徵值和特徵向量是矩陣”自己的”性質。什麼性質?就是 “座標系不變” (invariant) 的性質。
特徵值非常重要,體現了矩陣內稟的性質,和觀察者的座標無關:薛定諤方程中它對應能量,馬爾可夫均衡態計算的關鍵,微分方程中相圖的邊界,譜聚類中所謂的譜即特徵值,電路或是力學系統的共振頻譜。但由於只有方陣才有特徵值,實際應用中方陣較少,因此一般都會左自乘: $A^{T}A$ ,得到性質優良的對稱矩陣 $S$, $S$ 被Gilbert Strang稱為線性代數的皇帝。
1907年,奇異值 (Singular Value)的概念由德國數學家Erhard Schmidt提出 (Beltrami, Jodan 等幾位數學家都有貢獻),還記得 Gram-Schmidt 求標準正交基的方法嗎?所以” 正交“ 是 SVD 的核心概念。基本的概念是找到一個正交的坐標系 (V in self space), 在 linear transform 到新的 space 仍然正交形成新的坐標系 (U in mapped space)。奇異值就是對應每一個坐標軸的 scaling。因此都是正值或 0, 從大到小代表重要性。奇異值越小,代表在新的坐標系約被 scale down, inverse 的 error 越大;如果奇異值為 0 就代表該坐標軸消失而且無法 inverse. 最大奇異值方向就是矩陣最大作用方向。
當時Schmidt 也稱奇異值為 “eigenvalues”,即今天特徵值所用的詞,直到1937年,奇異值 “Singular value”這個詞才由 F. Smithies 開始使用。術語都曾是同一 eigenvalues,也難怪大家容易混淆。
數據時代,SVD 已成為最重要矩陣分解。它提供的數值穩定的矩陣分解方法,被廣泛應用於數據科學中:矩陣的低秩近似 (low rank approximation, ignore smaller singular values) 靠它,偽逆 (pseudo-inverse) 計算靠它,PCA的底層邏輯是它,它還非常靠譜,確保解存在,而特徵值就不好說了……奇異值這麼重要,但它到底“奇異”在哪?
EVD Vs. SVD 差異
定義不同
EVD ($A v | v$) : $A v = \lambda v$ 此處 A 是方陣 ($n\times n$),$\lambda$ is eigenvalues, 對應的 $v$ 稱為 eigenvectors.
- 可以證明:$A = Q D Q^{-1}$ 此處 $A, Q, D \in n\times n$: $D$ 是對角方陣 of eigenvalues (可以是複數值).
- $A v = Q D Q^{-1} v = \lambda_k v \to D Q^{-1} v = \lambda_k Q^{-1} v \to $ $\lambda_k$ 對應的 right (column) eigenvector 就是 $Q$ 的 $k$-th column vector.
-
$u A = u Q D Q^{-1} = \lambda_k u \to u Q D = u Q \lambda_k \to $ $\lambda_k$ 對應的 left (row) eigenvector 就是 $Q^{-1}$ 的 $k$-th row vector.
- 注意一般 $Q^T \ne Q^{-1} \equiv Q^T Q \ne I$. 也就是 $Q$ 的 column vectors ($A$ 的 eigenvectors) 並非正交。
- 只有 $A$ 是 symmetric matrix:$A^T = A \to A = QDQ^{-1}=Q D Q^T$ and $Q^T = Q^{-1}$,$Q$ 是單位正交矩陣 (orthonormal matrix),同時 $D$ 是實數 (real) 對角矩陣。
- 更 general $A$ 是 complex Hermitian matrix, i.e. $A^* = A$. 結論不變 : $Q^* = Q^{-1}$,同時 $D$ 是實數 (real) 對角矩陣。
SVD ($A v_1 \perp A v_2$ given $v_1\perp v_2$ ): $A = U \Sigma V^T$ 此處 $A, U, \Sigma, V$ 是矩陣, $n\times p, n \times n, n \times p, p \times p$, respectively, $U$ and $V$ 都是單位正交方陣 (orthonormal square matrix), i.e. $U^T = U^{-1}$ and $V^T = V^{-1}$, $\Sigma$ 是對角矩陣 ($n\times p$) of singular values (always non-negative real number!). 奇異值是非負實數,通常從大到小順序排列。
- 正交性和 SVD 關係:$V$ 和 $U$ 都是 rotation matrix 不會改變 $v_1$ 和 $v_2$ 的垂直關係。只有 $\Sigma$ 的 scaling 會改變 $v_1$ 和 $v_2$ 的夾角,除了 basis direction ($e_1, e_2$). 因此 singular vectors 在經過 $V$ transform 會是 align with basis direction ($e_1, e_2$). $V^T v_1 = e_1 \to v_1 = (V^T)^{-1} e_1 = V e_1$ 因此 $v_1$ 就是 $V$ 的 column vector 1, 同理 $v_2$ 就是 $V$ 的 column vector 2.
-
單位圓向量 map 對應最大和最小的向量也都是 eigen-vectors.
-
$v_1 \perp v_2 \to v_1^T v_2 = 0$ and $(A v_1)^T (A v_2) = v_1^T V \Sigma U^T U \Sigma V^T v_2 = v_1^T V \Sigma^2 V^T v_2 = e_1^T \Sigma^2 e_2 = 0$
- SVD 另一個數學表示是:$argmax_{|x|=1} |Ax|$ 對應最大作用方向。這個表示雖然有明確的幾何和物理意義,但無法涵蓋 SVD 其他方向。只能是部分表示 SVD。
EVD 和 SVD 數學上有關係嗎? Yes! 關係如下:
1. $A$ 是 $n\times n$ symmetric square matrix: $A = A^T$
-
EVD: $A = Q D Q^{-1} = (Q^{-1})^T D Q^{T} = A^T \to Q^T = Q^{-1}$
-
SVD: $ A = U \Sigma V = V^T \Sigma U^T = A^T \to U^T = U^{-1} = V , V^T = V^{-1} = U$
-
所以 $A = Q D Q^{-1} = U \Sigma U^{-1}$. 所以很自然推論: $Q = U, D = \Sigma, V=Q^{-1}$? Wrong!
- 因為 symmetric matrix 的 eigenvalues 是可正可負實數。但是 singular value 要求正實數或零。因此 $D \ne \Sigma$, $Q \ne U$. 不過差距也不大。
-
**正確的結論:$\Sigma = D $ , 對稱矩陣的奇異值等於特徵值的絕對值。但是 eigenvectors 可能正負號和 singular value vector 相反,所以 $Q$ 的 column vectors 和 $U$ 的 column vectors 最多差個正負號 ?!** -
For symmetric and Hermitian matrices, the eigenvalues and singular values are obviously closely related. A nonnegative eigenvalue, λ ≥ 0, is also a singular value, σ = λ. The corresponding vectors are equal to each other, u = v = x. A negative eigenvalue, λ < 0, must reverse its sign to become a singular value, σ = λ . One of the corresponding singular vectors is the negative of the other, u = −v = x.
2. $A$ 是 normal square matrix, $A$ and $A^T$ commute: $A A^T = A^T A$
-
注意所有的 matrix A 和 transpose matrix A’ 相乘都是 symmetric matrix, i.e. S = A A’ , S’ = (A A’)’ = A A’ = S. 不過這和 normal matrix 完全沒有關係!
-
Normal matrix 一定是 square matrix: 如果 A: n x p; A A’ : n x n; A’ A: p x p, 如果兩者 commute 代表 n = p.
-
如果 A 是 symmetric matrix, 一定是 normal matrix; 但反之不成立。例如 \(A = \left[\begin{array} {cc}1 & 1 & 0\\0 & 1 & 1 \\ 1 & 0 & 1\end{array}\right] \to \quad A A^T = \left[\begin{array} {cc}2 & 1 & 1\\1 & 2 & 1 \\ 1 & 1 & 2\end{array}\right] = A^T A\)
-
$A$ 的 eigenvalues $D_i$: 2, $(1\pm i \sqrt{3})/2$. $A$ 的奇異值 $\Sigma_i$:2, 1, 1. 奇異值是特徵值的絕對值 (包含複數) ! $\Sigma = D $
-
-
Normal matrix 的奇異值和特徵值的關係類似 symmetric matrix
- $A^T A = Q^T D (Q^{-1})^T Q D Q^{-1} = V^T \Sigma U^T U \Sigma V = V^T \Sigma^2 V$
- $A A^T = Q D Q^{-1} Q^T D (Q^{-1})^T = U \Sigma V V^T \Sigma U^T = U \Sigma^2 U^T $
-
$A^T A = A A^T \to \Sigma = D \ $ : 奇異值是特徵值在實數和複數的絕對值。
3. $A$ (n x p) 不是 normal 也不是 symmetric matrix, 甚至不是 square matrix
- 因爲不是 square matrix, 沒有特徵值或特徵向量! 但是有奇異值!
- 定義 $S = A^T A$ (pxp) 此時 $S$ 是 square and symmetric matrix, 所以有特徵值和奇異值。$S$ 的奇異值是特徵值的絕對值,以及原來 $A$ 奇異值的平方!
- 當然可以定義 $S = A A^T$ (nxn), 同樣的結論,depending on n > p 或是 p > n, 多出的奇異值為 0.
作用 (action) 不同
這裡的“作用” (action) 所指的矩陣與向量的乘積得到一個新的向量,幾何上相當於對向量進行了旋轉和拉伸,就像是對向量施加了一個作用 (action),或者說是變換。
- 特徵向量描述的是矩陣的方向不變作用 (invariant action) 的向量。更基本的觀念是座標系 (包含時間) 不變,因此 ED 廣泛出現在物理,幾何 (vector/tensor/geometric analysis).
- 奇異向量描述的是矩陣最大作用 (maximum action) 的方向向量。更基本的觀念是正交,因此是座標系 dependent (例如選擇一個非歐座標就會改變 singular value).
口説無憑,我們直接看例子就可以明白:
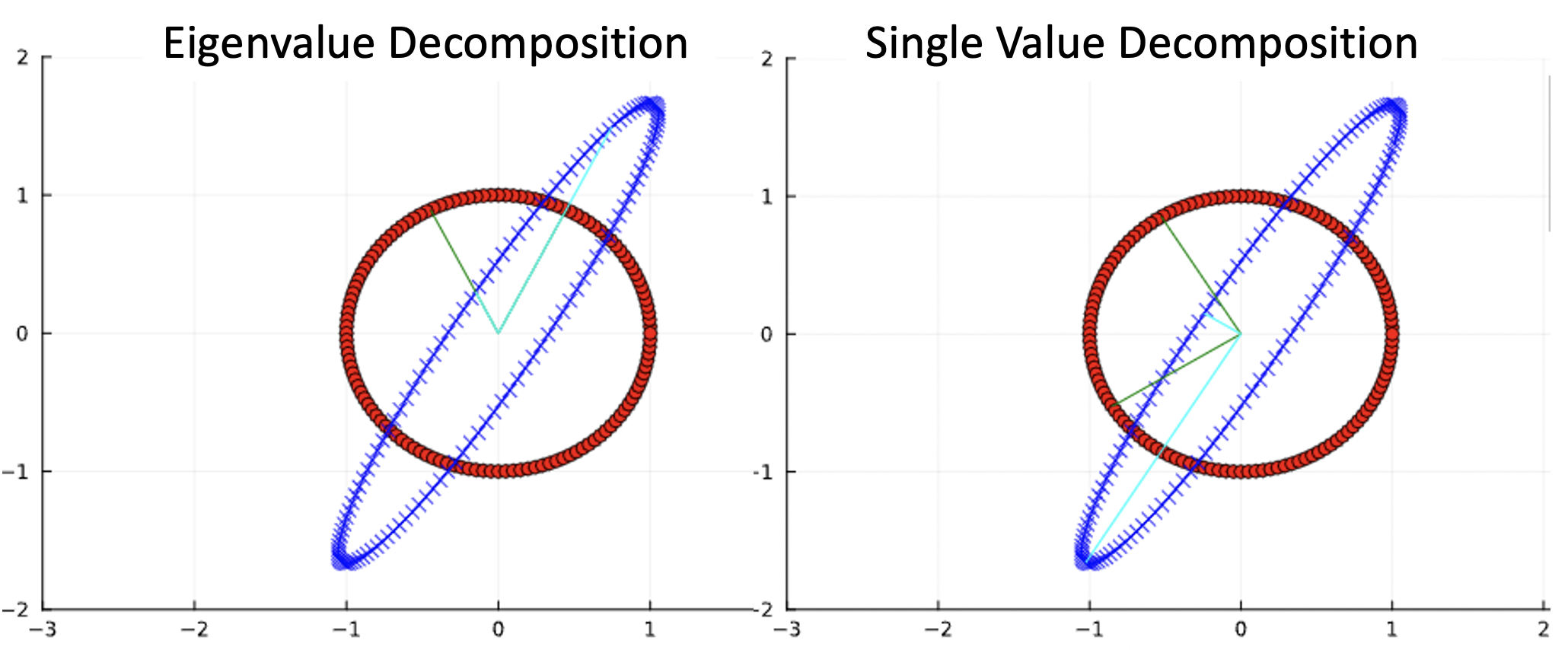
\[A= \left[\begin{array} {cc}1 & \frac{1}{3}\\ \frac{4}{3} & 1\end{array}\right]\]Eigenvalue decomposition 對應的 unit circle map 如下圖左,Single value decomposition 如下圖右。綠色向量是 unit circuit input, 藍色向量是 (橢圓) output.
- 下圖左 eigenvector 的 input 和 output 方向是沒有改變的。但是大小 (eigenvalues) 會改變。注意 eigenvectors 沒有正交,也沒有對應最大作用方向!特徵向量不變的方向並不保證是拉伸效果最大的方向,而這是奇異向量的方向。
-
下圖右 single vector 對應作用最大和最小的方向。注意不止 input vectors 正交,output vectors 也正交。
-
Eigenvalue: 5/3 (1.67) and 1/3 (0.33). (下圖左兩條藍色線的長度)
-
Eigenvector: [0.745, 1.491] and [-0.15, 0.3]. (下圖左兩條綠色線向量)
-
Single value: 1.95 and 0.28. (下圖右兩條藍色線的長度) 注意 single values 的最大值比 eigenvalue 大,最小值比 eigenvalue 小。
- Single vector: [-0.53, 0.85] and [-0.85, 0.53]. (下圖右兩條綠色線向量) 注意綠色向量是正交,而且 output 藍色向量也是正交!
Eigshow
Matlab 和 Julia 都有動畫式的 2D eigen vectors and singular vectors. 非常 cool 並且有 geometric sense. 大家可以試試!
應用不同
方向不變和拉伸最大都是矩陣內稟的性質,方向不變在馬爾可夫隨機場中非常重要;而拉伸最大的方向則是數據方差分佈最大的方向,所含信息量最大,是PCA等方法中的核心思想。如果要說“奇異”,大約就在於最大拉伸方向吧。
Eigenvalue 的應用範圍是當 $A$ matrix 的 linear transformation 是 it maps to itself, 所以只有在 nxn square matrix 才能定義 eigenvalue decomposition.
SVD 則沒有這個限制。 $A$ 可以從一個 space lnear transform 到另一個不同 rank 的 space (nxm) matrix.
EVD:
除了幾何 (coordinate) invariant 意義,還有物理和數學意義。
物理意義: 特徵值系統內稟的性質,和觀察者的座標無關:薛定諤方程中它對應能量,馬爾可夫均衡態計算的關鍵,微分方程中相圖的邊界,譜聚類中所謂的譜即特徵值,電路或是力學系統的共振頻譜。
其他意義 (machine learning? 黃金三角? S = A’ A)
數學意義:
$A^n = (QDQ^{-1})^n = Q D^n Q^{-1} \longrightarrow$
$ \exp(A) = Q \exp(D) Q^{-1}$
$ = Q \left(\begin{array} {cc}e^{\lambda_1} & 0 & \cdots \0 & e^{\lambda_2} & \cdots \ \cdots & \cdots & \cdots\end{array}\right) Q^{-1}$
$Q$ 不一定是orthonomal matrix, 只有在symmetric matrix 才是 orthonomal matrix!
SVD
幾何:” 正交“ 是 SVD 的核心概念。基本的概念是找到一個正交的坐標系 (V in self space), 在 linear transform 到新的 space 仍然正交形成新的坐標系 (U in mapped space)。奇異值就是對應每一個坐標軸的 scaling。因此都是正值或 0, 從大到小代表重要性。奇異值越小,代表在新的坐標系約被 scale down, inverse 的 error 越大;如果奇異值為 0 就代表該坐標軸消失而且無法 inverse. 最大奇異值方向就是矩陣最大作用方向。
SVD 比較像是找到正交的座標系經過轉換還是正交座標系。物理上似乎沒有特別偏好特殊的座標系,而是座標系無關。
在 machine learning, compression, optimization 卻很有意義而且有用,就是降維。把某些不重要的 dimension 忽略,例如 PCA!
SVD 可以幫助做 inverse 因爲有一個新的 coordinate system! 可以把 scaling 為 0 的 dimension 忽略!
Pseudo-inverse using SVD (Pseudo-Inverse of a Matrix (berkeley.edu))
The pseudo-inverse of a  matrix $A$ is a matrix that generalizes to arbitrary matrices the notion of inverse of a square, invertible matrix. The pseudo-inverse can be expressed from the SVD of , $A$ as follows.
matrix $A$ is a matrix that generalizes to arbitrary matrices the notion of inverse of a square, invertible matrix. The pseudo-inverse can be expressed from the SVD of , $A$ as follows.
Let the SVD of $A$ be \(A = U \left(\begin{array} {cc}S & 0\\0 & 0\end{array}\right) V^T,\)
where $U, V$ are both orthogonal matrices, and $S$ is a diagonal matrix containing the (positive) singular values of $A$ on its diagonal.
Then the pseudo-inverse of $A$ is the $n \times m$ matrix defined as
\[A^{\dagger} = V \left(\begin{array} {cc}S^{-1} & 0\\0 & 0\end{array}\right) U^T,\]Note that $A^\dagger$ has the same dimension as the transpose of $A$.
This matrix has many useful properties:
- If $A$ is full column rank, meaning rank$(A) = n \le m$, that is, $A^T A$ is not singular, then $A^\dagger$ is a left inverse of $A$, in the sense that $A^{\dagger} A = I_n$. We have the closed-form expression
- If $A$ is full row rank, meaning rank$(A) = m \le n$, that is, $A A^T$ is not singular, then $A^\dagger$ is a right inverse of $A$, in the sense that $A A^{\dagger} = I_m$. We have the closed-form expression
- If $A$ is square, invertible, then its inverse is $A^\dagger = A^{-1}$.
- The solution to the least-squares problem
with minimum norm is $x^{\ast} = A^{\dagger} y$.
實數對稱矩陣 or Complex Hermitian Matrix 定理
特徵值的重要定理:Courant-Fischer min-max theorem
本定理是針對複數 Hermitian matrix 或是實數矩陣, $A = A^*$ (complex matrix) or $A = A^T$ (real matrix)
實數對稱矩陣 (或複數 Hermitian matrix) 有獨特的地位:
- Eigenvalue decomposition (EVD, invariant basis) 和 Singular value decomposition (SVD, orthogonal basis) 的 eigen-values 和 singular values 以及 eigen-vectors 和 singular vectors 基本一樣,最多差一個正負號。代表 invariant eigenvectors 也是正交 basis.
- Eigenvalues 均爲實數,Eigenvectors 互相正交。證明很容易 $A x = A^* x = \lambda x \to x^* A = \lambda^* x^* \to x^* A x = \lambda^* x^* x \to x^* \lambda x = \lambda^* x x^* \to \lambda = \lambda^*$
- $x^* A x$ : 對於任意 column vector 向量 $x \in \C$, $x^* A x$ 為實數。(這對複數 vector 很重要,對於實數 vector trivial).
- 證明:$x^* A x = x^* Q D Q^* x = z^* D z = \sum_i \lambda_i |z_i|^2 \in \R$ 因爲 $\lambda_i \in \R$
- 以 2D SVD 爲例,正交 basis 就是單位圓 vector $|x|=1$ 經過 $Ax$ mapping 後產生最大和最小的 vector. 因爲是對稱矩陣,SVD 和 EVD 一致,所以 $\lambda_{max}$ 對應最大的 $|Ax|$, 所以 $\lambda_{min}$ 對應最小的 $|Ax|$
- $\lambda_{max} = \max \frac{x^* A x}{x^* x}$
- $\lambda_{min} = \min \frac{x^* A x}{x^* x}$
- 那麽 3D, 4D 或更高維的 eigenvalues 又是如何呢?這就是 Courant-Fischer min-max theorem
Rayleigh Quotient
-
定義 Rayleigh Quotient: $R = \frac{x^* A x}{x^* x}$ where $x \ne 0$
- Given $A$ 是 $n \times n$ 的 Hermitian matrix (or real symmetric matrix), eigenvalues 皆爲實數。假設 $\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_n$, 對應的正交 eigenvectors 為 $u_1, u_2, …, u_n$則有
- $\max R = \max \frac{x^* A x}{x^* x} = \lambda_1$ when $x = k u_1$
- $\min R = \min \frac{x^* A x}{x^* x} = \lambda_n$ when $x = k u_n$
-
證明:$R = \frac{x^* A x}{x^* x} = \frac{x^* Q D Q^* x}{x^* x} = \frac{z^* D z}{z^* z} = \frac{\sum_i \lambda_i z_i ^2 }{\sum_i z_i }$ 因此 $ \lambda_n \le R \le \lambda_1$ - $z = Q^* x$ 並且 $x^* x = z^* z$
- 直觀看出如果是和 $u_1$ 正交的空間 $(0, u_2, …, u_n )$ 的 Rayleigh Quotient 最大值是 $\lambda_2$, i.e.
- $\max_{x \perp u_1} \frac{x^* A x}{x^* x} = \max_{x \in (u_2, .. u_n)} \frac{x^* A x}{x^* x} = \lambda_2$
- 同樣的邏輯,$\max_{x \in (u_k, .. u_n)} \frac{x^* A x}{x^* x} = \lambda_k$
- 比較有趣是,最後 eigenvalue $\max_{x \in (u_n)} \frac{x^* A x}{x^* x} = \lambda_n = \min_{x} \frac{x^* A x}{x^* x}$
-
上式必須知道 $u_1$ 是否有方法繞過 $u_1$? Yes, 利用 min
-
考慮任意向量 $w \in \C$ 且 $x \perp w \to z \perp Q^* w$, 令 $V = {z z\perp Q^* w}$, 且 $V’ = {z z\perp Q^* w, z_3 = z_4 … = z_n =0}$, 則有 $V’ \subset V$ - $\max_{x \perp w} \frac{x^* A x}{x^* x} = \max_{z \perp Q^* w} \frac{z^* D z}{z^* z} = \max_{z \in V} \frac{z^* D z}{z^* z}$ $ \ge \max_{z \in V’} \frac{z^* D z}{z^* z} = \max_{z \in V’} \frac{\lambda_1 |z_1|^2 + \lambda_2 |z_2|^2}{|z_1|^2 + |z_2|^2} \ge \lambda_2$
- 等號成立當 $w = u_1$
-
-
因此 $\min_w \max_{x \perp w} \frac{x^* A x}{x^* x} = \lambda_2$
- 這公式有點難看懂。就是任意的 (n-1) 維子空間,所有最大值中的最小值是 $\lambda_2$. 仔細想一下,如果 $w \nparallel u_1$, (n-1) 維子空間一定包含 $u_1$, R 的最大值是 $\lambda_1$; 只有當 $w \parallel u_1$, (n-1) 維子空間不包含 $u_1$, R 的最大值是 $\lambda_2 \le \lambda_1$, 才是正解。因此可以用 $\min_w$ 取代 $w = u_1$.
-
反過來 $\max_w \min_{x \perp w} \frac{x^* A x}{x^* x} = \lambda_{n-1}$
- 就是任意的 (n-1) 維子空間,所有最小值中的最大值是 $\lambda_{n-1}$. 仔細想一下,如果 $w \nparallel u_n$, (n-1) 維子空間一定包含 $u_n$, R 的最小值是 $\lambda_n$; 只有當 $w \parallel u_n$, (n-1) 維子空間不包含 $u_n$, R 的最小值是 $\lambda_{n-1} \ge \lambda_n$. 因此可以用 $\max_w$ 取代 $w = u_n$.
-
同樣 $\min_{w_1, w_2} \max_{x \perp w_1, w_2} \frac{x^* A x}{x^* x} = \lambda_3$
- 就是任意的 (n-2) 維子空間,所有最大值中的最小值是 $\lambda_3$. 如果 (n-2) 維子空間包含 $u_1$ 或 $u_2$, R 的最大值是 $\lambda_1$ 或 $\lambda_2$; 只有當 (n-2) 維子空間不包含 $u_1, u_2$, R 的最大值是 $\lambda_3 \le \lambda_1, \lambda_2$, 才是正解。因此可以用 $\min_{w_1, w_2}$ 取代 $w_1 = u_1, w_2 = u_2$.
- 反過來 $\max_{w_1, w_2} \min_{x \perp w_1,w_2} \frac{x^* A x}{x^* x} = \lambda_{n-2}$
- $\max_{x \perp u_1} \frac{x^* A x}{x^* x} = \max_{x \in (u_2, .. u_n)} \frac{x^* A x}{x^* x} = \lambda_2$
Courant-Fischer Min-Max Theorem Summary
對於 $n \times n$ 的 Hermitian matrix (或是實數的對稱矩陣):
$\lambda_k$ 是 $k$-th 大的 eigenvalue, i.e. $\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_n$
- $\lambda_k = \min_{dim(V)=n-k+1} \max_{x \in V} R = \min_{dim(V)=n-k+1} \max_{x \in V} \frac{x^* A x}{x^* x}$
- $\lambda_k = \max_{dim(V)=k} \min_{x \in V} R = \max_{dim(V)=k} \min_{x \in V} \frac{x^* A x}{x^* x}$
經典應用: Wely Theorem
對於兩個 $n \times n$ 的 Hermitian matrix (or real symmetric matrix) $A$ and $B$:
\(\lambda_k(A) + \lambda_n(B) \le \lambda_k (A+B) \le \lambda_k(A) + \lambda_1(B)\) 有用的結論
-
兩個 Hermitian matrixes 的 eigenvalues 範圍
-
一個 Hermitian matrix 加上一個 semi-definite matrix (所有 eigenvalues 大於等於 0), eigenvalues 必增大