Reference
MacKay, “Information Theorym, Inference, and Learning Algorithm”, book.pdf (inference.org.uk)
Fake Coin Game
我在小學做的題目:
8 枚金幣其中有一枚比較輕的假金幣。有一把天平,最少需要幾次可以秤出假的金幣?
如果 80 枚金幣最少要秤幾次?
Wrong Ans: 這是一個陷阱題。如果不假思索,多半回答 3 次。每次秤金幣除 2,8 -> 4 -> 2 -> 1.
Right Ans: 正確答案是 2 次。每次秤金幣除 3,8 -> 3 -> 1. 或是 9 枚金幣只要秤 2 次,9 -> 3 -> 1.
同樣 80 枚金幣可以想成 81 枚,只要秤 4 次,81 -> 27 -> 9 -> 3 -> 1.
從數學的角度歸於等比級數問題,只是每次的比例是 3 而不是 2.
第一類問題:
- 任意 n 金幣最少要秤幾次? round (log_3 N)
- 雖然直覺這是最少的次數,如何證明 ?
- 這個數字和 information theory 的 uniform distribution entropy log_2 N 有點像,有任何關係嗎?
如何推廣?
第二類問題
加上一個條件,最多有一枚輕的假金幣 (i.e. 一枚假或是全為真)。8 or 9 枚最少秤幾次?
round (log_3 (N-1)). 如果 8 枚,還是 2 次,但是 9 枚則需要 3 次。因爲如果前兩次都平手,需要第三次決定是一枚假金幣或是沒有假金幣。
更複雜是最多有 k 枚輕的假金幣。應該很複雜!!
第三類問題
8 枚硬幣其中有一枚僞幣,但我們不知道是比較輕或重。有一把天平,最少需要幾次可以秤出僞幣?而且還要知道是比較輕或是比較重。也有可能沒有僞幣。
12 枚呢?
Wrong Ans: 就是上述答案 + 1 次。可以推理 3 枚時,需要 2 次才能判斷 (correct)。8 枚時 3 次 (correct), 12 枚 4 次 (Wrong!) etc. In general: round (log_3 N) +1 (Wrong!)
Right Ans: 3 枚 2 次,8 枚 3 次,但 12 枚只要 3 次而非 4 次!!
Question 1: 是否有 (upper/lower) bound 最少要秤幾次?
Yes, 使用 hypothesis number reduction 觀念
例如 3 枚金幣:
第一類: 1+, 2+, 3+: 3
第二類: 1+, 2+, 3+, 0: 4
第三類: 1+, 2+, 3+, 1-, 2-, 3-, 0: 7
每次天平秤,hypothesis 最多 divide by 3.
| 秤次數 | 第一類 | 第二類 | 第三類 |
|---|---|---|---|
| 1 | 3 (3H) | 2 (3H) | X |
| 2 | 9 (9H) | 8 (9H) | 3 (7H) |
| 3 | 27 (27H) | 26 (27H) | 12 (25H) |
| 4 | 81 (81H) | 80 (81H) | 40? (81H) |
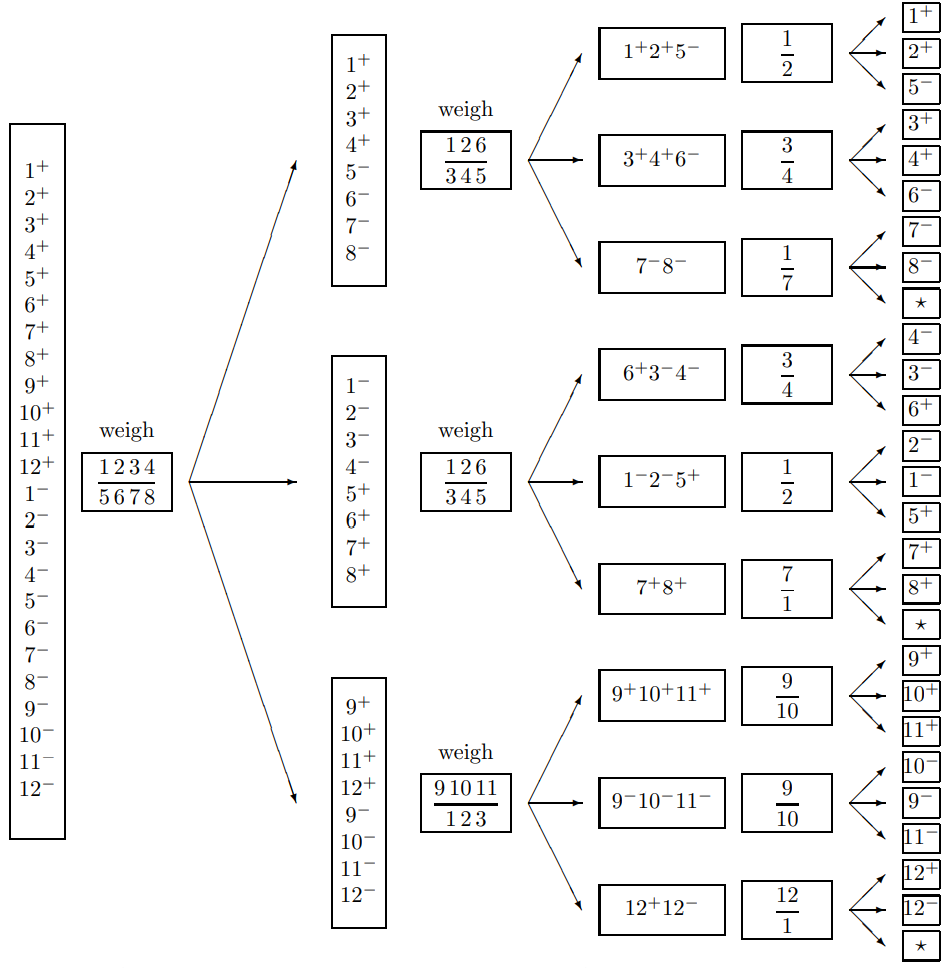

From information theory viewpoint:
N: number of states
Successive information extraction (from Shannon’s xxx theorem of page. xx in reference)
log_2^3 = 1.58 bit (assuming equal outcome)
12 gold coin = (24 or 25 states) = log_2 25 / 1.58 = 2.92 次c