Information Theory For Source Compression

Posted on | In

用 Fake coin hypothesis 思考 information theory 如何使用非 constructive method to prove things.

Major Reference

book.pdf (inference.org.uk) from MacKay 是經典 information theory textbook.

(1) High Probability Set vs Typical Set - YouTube

Information Theory Application

Shannon 的信息論 (Information Theory) 包含兩個部分:

Information Source Noisy Channel
Application Compression Communication
Source/Channel
Capacity		 Source entropy: $H(X)$ Max source/receiver
mutual-info: $\max I(X;Y)$
Shannon Theory Source Coding Theorem Channel Coding Theorem

本文聚焦在 source code 也就是 data compression 部分。下文討論 noisy channel communication.

Source Compression

直觀壓縮

Symbol (Lossless) Compression

最常見且容易理解的是 variable length symbol encoding, 例如以下 6-symbol 理論上需要 3-bit ($2^3 = 8 > 6$) to encode.

如果 symbols 出現的頻率不同，可以根據出現的頻率 (機率) encode, 如下圖。例如 “a” 最常出現，直接 encode 為 “0”, 只要 1-bit. “b,r,d” encode 成 3-bit. 最少出現的 encode 成 4-bit. 假設 “a” 的機率是 0.5, “b,r,d” 是 “0.125”， “r,!” 是 0.0625.

如此平均的長度是: $0.5 \times 1 + 3 \times 0.125 \times 3 + 2 \times 0.0625 \times 4= 2.125$ bits. 壓縮率為 2.125/3 = 71%, 也就是省了 30%.

  • 注意此處假設不用 start-bit indictor, 而是 first match, 例如 01101100111010101011 = 0’110’110’0’111’0’1010’1011=arraba!c
  • 沒有 start-bit indictor 要確定 code 不會有 ambiguity. 一般壓縮還是會加上一些 check bit 避免 error propagation.
  • 如果每個 symbol 出現的頻率都一樣，顯然這樣的壓縮無效，反而多此一舉。存在其他壓縮的方法嗎？如何證明沒有更好的壓縮？

image-20230120152944731

Shannon 定義 information 的度量 (self)-entropy: $H(X) = - \sum_i p_i \log_2 p_i$

Shannon 天才之處是看到 information entropy 和壓縮的關係。例如我們可以計算 6-symbol 的 entropy.

$H(X) = - (0.5 \log_2 0.5 + 3 \times 0.125 \log_2 0.125 + 2 \times 0.0625 \log_2 0.0625) = 2.125$ bits

這是巧合? 顯然不是。我們再看一個例子。

Ensemble Compression

如果一個 binary coin with biased probability p. 例如 p = 0.02. 如何壓縮？ 另外 entropy $H_2(0.02) = 0.141$-bit, 如何連結？

這是 binary outcome $\mathcal{A}_X$ = {H:0, T:1}, 不像剛才的 6-symbol case, 至少要 1-bit to encode H or T. 似乎無法直接壓縮 1-bit, 如何解決？

一個聰明的想法是集合 N-bits 再壓縮, i.e. ensemble compression。

  • $\mathcal{A}_X^N = {HH..H, HH..T, …}$ 共有 $2^N$ sequences. 每一個 sequence 的長度是 N.

假設 p 很小，很大的機率會出現 HHHH..HTHHHHTH .. 可以出現連續 H 時，只要用數字代表，不需要真的存所有的 H. 例如 10H, instead of HHHHHHHHHH (10-bit), 只要存 10H (4+1=5 bit, 1 是 indicting start bit). 但是因爲出現 T 的機率很小 (p=0.02), 就直接存 T.

例: THHHHHHHHHHTHHHHHTHHHHHHHHHT = ‘T’HHHHHHHHHH’T’HHHHH’T’HHHHHHHHH’T = “1”0“1010”1”0”0101”1”0“1001”1”

  • T 直接用 1 代表, 如果有連續的 1，直接用 11…1。如果 $p$ 很小，連續 1 的機會非常小。
  • H 用 leading 0 加上 4-bit encode 連續的 0. 因此最多 encode 15 個連續的 0. 如果超過 15 個連續的 0, 可以用特別的 code 暗示, 例如 0000 代表。所以 18 個連續的 0, 可以用 “0”0000”0010” encode. 第一個 0 代表一個或連續的 0 開始，0000 代表超過 16 個 0，接下的 0010 代表 2 個連續的 0. 所以共有 16+2=18 個連續 0.
  • 可以用比 4-bit 更多 bit encode 連續 0 嗎？Yes, 但顯然和連續 0 長度發生的機率有關。$p$ 越小，發生長連續 0 的機會越大，用更多的 bits encode 連續 0 會得到更好的壓縮率。不然增加連續 0 encode bits 反而是 overhead. 所以對於每一個 $p$ 應該都有最佳的 bits to encode 連續 0.
  • 考慮 ensemble length N = 100 and $p=0.02$. 連續 0 出現 sequence 的機率如下：
    • sequence with no 1, 100 連續 0: $(1-p)^{100} = 0.1326$ (most probable)
    • sequence with a single 1, 視為 2 段 連續 0: $(1-p)^{99} p = 0.0027$ x 100 sequences = 0.27
    • sequence with a two 1’s, 視為 3 段 連續 0: $(1-p)^{98} p^2 = 5.25\times 10^{-5}$ x 4950 sequences = 0.2734 (most typical)
    • sequence with a three 1’s, 視為 4 段 連續 0: $(1-p)^{97} p^3 = 1.12\times 10^{-6}$ x 161700 sequences = 0.1823
    • sequence with a four 1’s, 視為 5 段 連續 0: $(1-p)^{96} p^4 = 2.3\times 10^{-8}$ x 3.9M sequences = 0.09
    • Other: 小於 5% 機率。

  • 因為連續 0 的長度可以到 100, 我們用 7-bit encode 連續 0 (最多 127 個)

  • N= 100 ensemble 用以上方法壓縮的初估平均長度：0.1326 * 1 * (1+7) + 0.27 * 2 * (1+7) + 0.2734 * 3 * (1+7) + 0.1823 * 4 * (1+7) + 0.09 * 5 * (1+7) = 21.376 bits, 顯然比不壓縮的 100-bit 好不少。此處 *1 *2 *3 代表有 1 代表 encode 1,2,3 段連續 0, etc.
  • 圖像其實使用類似的 compression 方法，因為同一區塊常常有同樣的顏色。
  • 如果 $p$ 很大，顯然這種壓縮無效，反而增加 overhead.
  • 有更好的壓縮方法嗎？21.376-bits 除以 100 -> 平均 0.214 bits, 比 H(0.02) = 0.141-bit 大。

Question

  1. 有更好的方法? 例如用 1000-bit?

  2. What is the fundamental limitation or bound?

Ensemble Compression on Typical Set

Shannon 天才之處在於他看出

  • N 很大時，只需要 encode typical set sequences！ 因為非 typical set sequences 發生機率是任意小。
    • 這是大數法則，重要性常常被忽略！
    • 如果直接忽略其他 sequences，就是 lossy encode/compression
    • 如果不忽略，還是可以 encode 這些 sequences 用比較長的 bits (如例一的 “c” or “!”) encode. 因為非 typical set 出現機率很小，增加的 content 非常有限。
  • Typical set 的 number of sequence $ \to 2^{n H(X)}$ 當 $n \to \infty$ (見 Appendix)
  • 因為只需要 encode $2^{n H(X)}$ sequences, 如果 $2^{nH(X)} \ll 2^n \to H(X) \ll 1$ 可以達到壓縮的效果。
    • $H(X)$ 愈小，Information 愈少，代表 redundancy 愈多，壓縮率愈大。
    • $H(X) = 1$ for binary outcomes or $H(X) = log_2 S$ for S outcomes, 代表uniform random sequences 無法壓縮。

Typical Set Vs. N

再看一個 P(H) = 0.2, P(T) = 0.8 的例子。

  • N=5:

    image-20230115134815304

  1. Most probable: P(TTTTT) = 0.32768 (32.768%), 但是只有 C(5,0) = 1 case.

  2. Most typical: P(HTTTT) = 0.08192, 但是有 C(5,1) = 5 cases, 所以 total probability = 0.4096 (40.96%). 比 1 的機率更大。

  3. P(HHTTT) = 0.02048, 共有 C(5,2) = 10 cases, total probability = 0.2048 (20.48%). 排名第三。

  4. P(HHHTT) = 0.00512, 共有 C(5,3) = 10 cases, total probability = 0.0512 (5.12%)

  5. P(HHHHT) = 0.00128, total probability = 0.00128 x C(5,4) = 0.0064 (0.64%)

  6. P(HHHHH) = 0.00032 (0.032%), C(5,5)=1

推廣到 N = 10 和 N = 100 如下圖右一和右二。基本上以 fraction of tails = 0.8 (對應 P(T) = 0.8 ) 爲中心，在 N=100 大約 +/-10% (0.7-0.9) 範圍内的機率接近 98%, 其他可能出現的機率可以忽略不計，這就是 typical set 的概念。

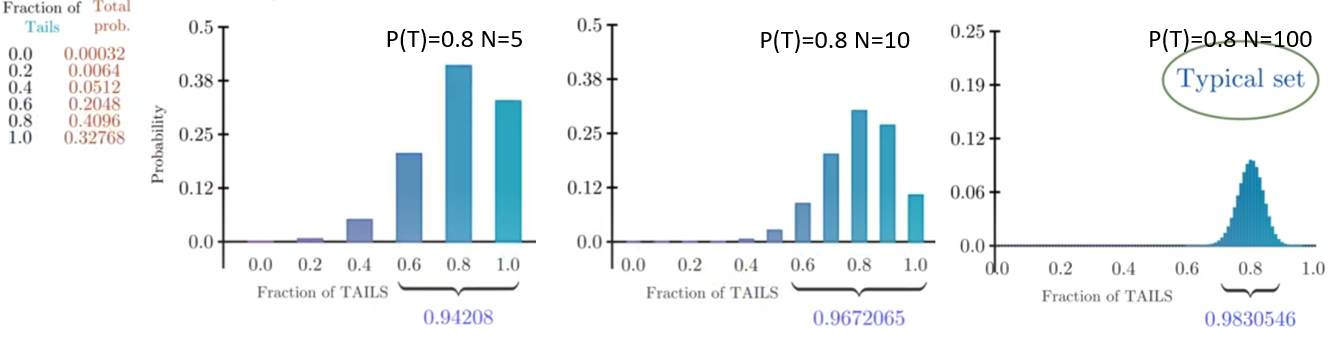
image-20230115141348762

  • 幾個問題: (i) 到底 +/- 多少範圍之外機率可以忽略不計? (ii) 這和 biased coin 的 entropy 有什麽關係? (iii) 到底有多少 sequences 是 typical set? (iv) 如何做 compression?
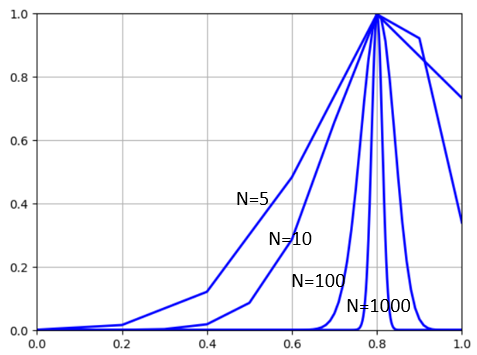
  • 第一個問題：如果我們從 N=5,10,100, 可以推論這個範圍是和 N 大小有關。 N 愈大，這個範圍就越集中在 0.8 附近。如果 N 非常非常大，我們甚至可以視爲就是在 0.8 占據了所有的機率分佈。下圖把 N = 5,10,100,1000 畫在一起，同時把機率乘上 $\sqrt{N}$ 同normlize peaks to 1 方便比較。可以看到的確如此。其實這就是有名的 ”Law of Large Numbers” 大數法則。當 $N$ 夠大，只有在 0.8 附近才有可能找到 sequences.

image-20230115233009749

  • 第二個問題：這裏 0.8 非常直觀，就是 P(T)=0.8. 但是對於比較複雜 case, 例如 multiple symbol (6 個或是 26 字母) 就沒有這麽直觀。所以我們還是要用數學。因爲 $H(X) = -0.2 \log_2 0.2 - 0.8 \log_2 0.8 = 0.722$-bit. 如果 N 是 i.i.d.

  • 第三個問題：$2^n$ 中的 $2^ {nH(X)}$ 比例。H(0.2) = 0.722-bit, 雖然 sequence 隨著 N 變大變多，但是 ratio 卻是變少

      all sequence typical set (> 9x%) Percentage
    N=5 32 12 0.38
    N=10 1024 149 0.16
    N=100 $1.3\times10^{30}$ $5.4\times10^{21}$ $4.2\times10^{-9}$
    N=1000 $10^{301}$ $2.2\times10^{217}$ $2.2\times10^{-84}$
  all sequence (2^N) typical set
C(n,k), k/n=0.2		 typical set
percentage		 Typical set
probability
N=5 32 C(5,1) = 5 0.38  
N=10 1024 C(10,2) = 90 0.16  
N=100 $1.3\times10^{30}$ C(100,20) $4.2\times10^{-9}$  
N=1000 $10^{301}$ C(1000,200) $2.2\times10^{-84}$  
  • 寫成數學模式：我們從 Law of Large Numbers 出發

Recap Stirling’s approximation of C(N, m)

Shannon Source Coding 理論

核心在於 AEP (Asymptotic Equipartition Principle).

image-20230117212623939

image-20230118235336289

Typical Set and AEP Principle

Typical set $A^n_{\varepsilon}$ 的定義如下： \(A^n_{\varepsilon}=\left\{\left(x_1, \cdots, x_n\right):\left|-\frac{1}{n} \log p\left(x_1, \cdots, x_n\right)-H(X)\right|<\varepsilon\right\} .\)

  • AEP 的 typical set 有 $ \mathcal{A}^n = 2^{n H(X)}$ sequences. 每一 sequence 都是 equal probability, i.e. $2^{-n H(x)}$. 檢查一些特例:
    • $p(H) = 0 \text{ (or 1) } \to H(X) = 0, \, nH(X) = 0$. 所以 $p(HHH…H)=1 \text{ or } p(TT…T)=1$, 其他 $2^n -1$ sequences 機率都是 0. 因此 AEP 只有一條 sequence, $ \mathcal{A}^n = 2^{n H(x)} = 1$.
    • $p(H) = 0.5 \to H(X) = 1,\, nH(X) = n$. 所有 $2^n$ sequences 機率都是 $2^{-n}$. $ \mathcal{A}^n = 2^{n H(x)} = 2^n$.

  • AEP 所佔的機率，當 $n\to \infty$ P(AEP) $\to$ 1.

  • AEP 的觀念是從統計力學而來，在熱平衡態，每一個分子的平均能量都是 $\frac{3}{2} kT$.

AEP 如何用於壓縮?

以下是“思想實驗”，並非真正的實踐方式。這也是 Shannon source coding and channel coding 被稱爲 non-constructive theory, 沒有提供可以實踐的方式。這不是壞事，至少培養了幾十萬個 PhD 以及十萬或百萬的 papers.

  • 原始 sequences 共有 $2^n$, 除非 {H,T} 數目一樣，彼此的機率不相同。但可以應用 AEP 的結論，只需要 encode 其中 $2^{n H(X)}$ sequence. 其他 {$2^n - 2^{n H(X)}$} sequences 可以直接忽略，因爲發生的機率可以忽略不計。
    • 如果不想忽略其他 sequences, 也可以 encode 成 n-bit sequence, 因為所佔的比例非常小，對於壓縮比例影響不太。
  • 我們可以事先做一個 codebook 給 encoder 和 decoder, 如何 index 這 $2^{n H(X)}$ sequences.
  • 因此只需要存或傳 indexes 就可以達到壓縮的目的！只要 $\log_2 2^{nH(X)} = n H(X)$ bits! 不需要 n bits.

Typical Set Definition

Typical set $A_n^{\varepsilon}$ 的定義如下： \(A_n^{\varepsilon}=\left\{\left(x_1, \cdots, x_n\right):\left|-\frac{1}{n} \log p\left(x_1, \cdots, x_n\right)-H(X)\right|<\varepsilon\right\} .\) The Asymptotic Equipartition Property (AEP) shows that for large enough $n$, the probability that a sequence generate by the source lies in the typical set, $A_n^{\varepsilon}$, as defined approaches one. In particular, for sufficiently large $n$, $P\left(\left(X_1, X_2, \cdots, X_n\right) \in A_n^{\varepsilon}\right)$ can be made arbitrarily close to 1 , and specifically, greater than $1-\varepsilon$ (See AEP for proof). The definition of typical sets implies that those sequences that lie in the typical set satisfy: \(2^{-n(H(X)+\varepsilon)} \leq p\left(x_1, \cdots, x_n\right) \leq 2^{-n(H(X)-\varepsilon)}\) Note that:

  • The probability of a sequence $\left(X_1, X_2, \cdots X_n\right)$ being drawn from $A_n^{\varepsilon}$ is greater than $1-\varepsilon$.
  • $\left A_n^{\varepsilon}\right \leq 2^{n(H(X)+\varepsilon)}$, which follows from the left hand side (lower bound) for $p\left(x_1, x_2, \cdots x_n\right)$.
  • $\left A_n^{\varepsilon}\right \geq(1-\varepsilon) 2^{n(H(X)-\varepsilon)}$, which follows from upper bound for $p\left(x_1, x_2, \cdots x_n\right)$ and the lower bound on the total probability of the whole set $A_n^{\varepsilon}$.
    Since $\left A_n^{\varepsilon}\right \leq 2^{n(H(X)+\varepsilon)}, n(H(X)+\varepsilon)$ bits are enough to point to any string in this set.

image-20230117212714807

In the last three chapters on data compression we concentrated on random vectors x coming from an extremely simple probability distribution, namely the separable distribution in which each component xn is independent of the others.

Step 1: lossy compression with fixed length

  • use fixed length n, of 1 word, total words K < 2^n. compute Hx, n > Hx 因爲 fixed length n 一定有 redundancy.
  • use group of N: with compression: total length = N x n.
  • With lossy compression, N x Hx.
  • Assuming binary with p = 0.5. Hx = 1 bit. N x 1bit = N bit, 也沒有 compression value.
  • Assuming binary with p = 0.1, Hx = 0.47bit. N x 0.47bit = 0.47N bit. 比起 N-bit compress 50%!
  • 如果 lossy compression with fixed length n, 在小於 N x Hx 一定無法 recover. 但是大於 N x Hx 可以忽略 lossy part with any error (to be proved).

image-20230108122345767

image-20230108122516575

Step 2: lossless compression with variable length

  • 1 word use variable length of Hx already!
  • N words. 當然也是 N x Hx.

image-20230108122626169

Lossless coding example:

Huffman coding

Lempel-Ziv coding

image-20230114232723671

Appendix

A: Stirling’s approximation and C(N, m)

從 Poisson distribution with mean $\lambda$ 開始：

\(P(r \mid \lambda)=e^{-\lambda} \frac{\lambda^r}{r !} \quad r \in\{0,1,2, \ldots\}\) For large $\lambda$, this distribution is well approximated - at least in the vicinity of $r \simeq \lambda$ - by a Gaussian distribution with mean $\lambda$ and variance $\lambda$ : \(e^{-\lambda} \frac{\lambda^r}{r !} \simeq \frac{1}{\sqrt{2 \pi \lambda}} e^{-\frac{(r-\lambda)^2}{2 \lambda}} .\) Let’s plug $r=\lambda$ into this formula, then rearrange it. \(\begin{aligned} e^{-\lambda} \frac{\lambda^\lambda}{\lambda !} & \simeq \frac{1}{\sqrt{2 \pi \lambda}} \\ \Rightarrow \lambda ! & \simeq \lambda^\lambda e^{-\lambda} \sqrt{2 \pi \lambda} \end{aligned}\) This is Stirling’s approximation for the factorial function. \(x ! \simeq x^x e^{-x} \sqrt{2 \pi x} \Leftrightarrow \ln x ! \simeq x \ln x-x+\frac{1}{2} \ln 2 \pi x .\) We have derived not only the leading order behavior, $x ! \simeq x^x e^{-x}$, but also, at no cost, the next-order correction term $\sqrt{2 \pi x}$. We now apply Stirling’s approximation to $\ln C(n,k)$ : \(\ln C(n,k) = \ln \frac{n !}{(n-k) ! k !} \simeq(n-k) \ln \frac{n}{n-k}+ k \ln \frac{n}{k} .\) Since all the terms in this equation are logarithms, this result can be rewritten in any base. We will denote natural logarithms $\left(\log _e\right)$ by ‘ln’, and logarithms to base $2\left(\log _2\right)$ by ‘ $\log$ ‘. 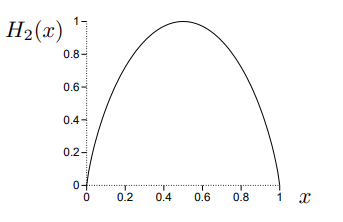If we introduce the binary entropy function, \(H_2(x) \equiv x \log_2 \frac{1}{x}+(1-x) \log_2 \frac{1}{(1-x)},\) image-20230115215417473

then we can rewrite the approximation as \(\log_2 C(n, k) \simeq n H_2(k / n),\) or, equivalently, \(C(n, k) \simeq 2^{n H_2(k/n)} .\) If we need a more accurate approximation, we can include terms of the next order from Stirling’s approximation: \(\log_2 C(n,k) \simeq n H_2\left(\frac{k}{n}\right)-\frac{1}{2} \log_2 \left[2 \pi n \frac{n-k}{n} \frac{k}{n}\right] .\)

B: Typical Set and AEP Principle

以上 n repeated coin with k heads: $C(n,k)$ 只有考慮 sequences, 如果再加上 probability

$p(H=k,T=n-k) = C(n, k) p^k (1-p)^{n-k}$

$ \log_2 p(H=k,T=n-k) = \log_2 C(n,k) + k \log_2 p + (n-k) \log_2 (1-p) = \log_2 C(n,k) + n { \frac{k}{n} \log_2 p + (1-\frac{k}{n}) \log_2 (1-p) }$

$= \log_2 C(n,k) - n H_2(\frac{k}{n}, p)$ 第二項是 cross-entropy

$\approx n H_2(\frac{k}{n}) - n H_2(\frac{k}{n}, p)$

$= -n \, KL(\frac{k}{n}| p) \le 0$ KL 是 KL divergence, always 大於等於 0。負的 KL divergence 自然小於等於 0.

等號成立條件 $\frac{k}{n} = p$ , 即是 $k = np$. 其實就是大數法則。

當 $n$ 夠大，除了 $k = np$ 的 $\log_2 p(H=np,T=n(1-p)) = 0 \to p(H=np,T=n(1-p)) = 1$. 其他所有的 sequences $\log_2 p(H=k,T=n-k) \to -\infty$, 也就是 $p(H=k, T=n-k) \to 0$.

$p(H=k,T=n-k)$ 對應的 number of sequence 就是 $C(n,k) \approx 2^{n H_2(k/n)} = 2^{n H_2(p)}$. 另外每一條 sequence 都是 equal probability! 這就是 AEP principle.

另一個 AEP principle 的表示法：

C: Stirling’s approximation of multi-values

以上 A and B 是 binary results, e.g. X = {H, T}, repeat n 次的結果，可以推廣到 multi-values. 先簡化成 3 個 results, e.g. X = {R, G, B}, repeat n 次的結果。四個五個或是多個 results 可以類推，不再贅述。

$p(k, m, n) = \frac{n!}{k! l! m!} p^k q^l s^m$ 此處 $k+l+m=n$ 以及 $p+q+s=1$

同樣利用 $x! \simeq x^x e^{-x}$

$ \log_2 p(R=k,G=l,B=m) \simeq n \log_2 n - k \log_2 k - l \log_2 l - m \log_2 m + k \log_2 p + l \log_2 q + m \log_2 s $

$= (k+l+m) \log_2 n - k \log_2 k - l \log_2 l - m \log_2 m + k \log_2 p + l \log_2 q + m \log_2 s $

$ = k \log_2 \frac{n}{k} + l \log_2 \frac{n}{l} + m \log_2 \frac{n}{m} + k \log_2 p + l \log_2 q + m \log_2 s $

$ = n (\frac{k}{n} \log_2 \frac{n}{k} + \frac{l}{n} \log_2 \frac{n}{l} + \frac{m}{n} \log_2 \frac{n}{m} + \frac{k}{n} \log_2 p + \frac{l}{n} \log_2 q + \frac{m}{n} \log_2 s) $

$= n H([\frac{k}{n}, \frac{l}{n}, \frac{m}{n}]) - n H([\frac{k}{n}, \frac{l}{n}, \frac{m}{n}], [p,q,s]) $

$ = -n \, KL([\frac{k}{n}, \frac{l}{n}, \frac{m}{n}] | [p,q,s]) \le 0$ 等號成立條件 $[\frac{k}{n},\frac{l}{n}, \frac{m}{n}] = [p, q, s]$.

當 $n$ 夠大，除了 $[\frac{k}{n},\frac{l}{n}, \frac{m}{n}] = [p, q, s]$ 的 $\log_2 p(R=np,G=nq,B=ns) = 0 \to p(R=np,G=nq,B=ns) = 1$. 其他所有的 sequences $\log_2 p(R=k,G=l,B=m) \to -\infty$, 也就是 $p(R=k,B=l,G=m) \to 0$.

$p(R=np, G=nq, B=ns)$ 對應的 number of sequence 就是 $\approx 2^{n H(X)}$. 每一條 sequence 都是 equal probability! 這是推廣的 AEP principle. 對於 general multi-values case 皆為真。

D: N Repeated Coin Distribution Vs. Binomial Distribution, Probability and Entropy

我常常會混淆 N repeated biased coin distribution vs. binomial distribution.

N repeated biased coin distribution

Let $X_1, X_2,\cdots, X_n$, 是 repeated i.i.d. of biased coin with HEAD probability $P(X=\text{H}) = p$; $P(X=\text{T}) = q = 1-p$.

  • $\mathcal{A}^n = { X_1, X_2,\cdots, X_n }$ , 一共有 $2^n$ samples (sequences).

  • Example sequence probability 如 $P({ H, H, \cdots, H, T})= p^{n-1} q = p^{n-1} (1-p)$.

  • $n H$ and $0 T$ 的 sequence 有 $C(n,0) = 1$ 條
  • $(n-1) H$ and $1T$ 的 sequences 有 $C(n,1) = n$ 條
  • $(n-2) H$ and $2T$ 的 sequences 有 $C(n,2) = n (n-1) / 2$ 條
  • $(p + q)^n = 1^n = C(n,0) p^n + C(n,1) p^{n-1} q + \cdots + C(n,k) p^{n-k} q^k + \cdots+ C(n,n) q^n = 1$
  • 所以 $k H$ and $(n-k) T$ 的 sequences 機率: $C(n,k) p^{n-k} q^k$, 同時 $\sum_{k=0}^{n} C(n,k) p^{n-k} q^k = 1$.
  • Entropy of 1 biased coin: $H(\text{1 biased coin}) = H_2(p) = - p \log_2 (p) - q \log_2(q) = - p \log_2 (p) - (1-p) \log_2(1-p)$
    • $H_2 (0) = H_2 (1) = 0$; $H_2 (0.5) = 1$ (bit)
  • Entropy: $H(\text{n biased coin}) = - \sum C(n,k) p^{n-k} q^k \log_2 (p^{n-k} q^k)$. 不過因爲每一次 biased coin 是 i.i.d. Entropy 可以直接相加！
  • Entropy: $H(\text{n biased coin}) = n H_2(p) = - np \log_2 (p) - nq \log_2(q) = - np \log_2 (p) - n(1-p) \log_2(1-p)$

Binomial Distribution

我們稍微修正 $H = 1$ and $T = 0$

$P(X=1) = P(X=\text{H}) = p$; $P(X=0) = P(X=\text{T}) = q = 1-p$.

另外定義 $S_n = X_1 + X_2 + \cdots + X_n$

  • $S_n$ 一共有 $n+1$ samples. $S \in [0,n]$.

  • $P(S_n =0) = C(n,0) p^n = p^n$

  • $P(S_n =1) = C(n,1) p^{n-1}q = n p^{n-1}q$

  • $P(S_n =2) = C(n,2) p^{n-2} q^2 = \frac{n(n-1)}{2} p^{n-2}q^2$

  • $P(S_n =k) = C(n, k) p^{n-k} q^k$. $\sum_{k=0}^n P(S_n =k) = C(n,k) p^{n-k} q^k = 1$. 這個部分和 N repeated biased coin 數學形式完全一樣。

  • 注意: Binomial 和 N repeated coin 不同點是在 Entropy!

    • $n = 1$, Entropy: $H(S_1) = H_2(p) = - p \log_2 (p) - q \log_2(q) = - p \log_2 (p) - (1-p) \log_2(1-p)$

    • In general, Entropy: $H(S_n) = - \sum_{k=0}^n C(n,k) p^{n-k} q^k \log_2 ( C(n,k) p^{n-k} q^k)$.

    • 注意多了一個 $C(n,k)$ factor 在 entropy 中！所以 binomial distribution entropy 和 N repeated coin entropy 不同！

    • 因爲 $H(S_2) \ne 2 H_2(p)$ 事實上因爲有 dependency 關係，$H(S_2) < 2 H_2(p)$. In general $n H_2(p) > H(S_n)$ when $n > 1$!

    • 上述不等式，直覺 make sense, 因為 N repeated coin 包含的 information (entropy) 比起只有多少 H 更多。

Citation