Takeaway
- 黎曼 (Riemann) 可積分一定勒貝格 (Lesbegue) 可積分
我不認為豎著切和橫著切本質是一樣的。雖然對於連續函數兩者的值是一樣的，但本質上的區別在於單調性，和隨之而來的完備性。
黎曼積分我們在豎著切的時候，由於我們對函數的波動起伏沒有假設，所以，每一個切片的大小都是未知的。每次細化切分/改變每段的參照點的時候，帶來的面積變化也是不固定的。
但對於勒貝格積分，由於只是在考慮單值函數下面的陰影面積，所以當我們橫著切的時候（用step function逼近的時候），我們可以保證切面的測度是隨高度單調遞減的。就像漢諾塔（或者我失敗的堆成小山一樣的午餐三明治），下面的一層總是比上面的高。所以我們每次細化切分/改變參照點的時候，面積的變化是單調的。從而單調收斂定理保證，我們總可以用簡單函數逼近得到勒貝格積分的值。而這種來自於單調收斂定理的對極限的封閉的完備性，正是我們引入勒貝格積分的重要原因之一。
- 一般情況下涉及到具體計算都會使用黎曼積分， 況且大多數情況下他們是相等的。
- 至於勒貝格積分的範圍比黎曼積分的範圍廣也是錯的，存在黎曼可積但是勒貝格不可積的函數，反之亦然。
從兩種積分本身的性質來看，Lebesgue積分是絕對收斂的積分，而Riemann積分不是。具體地說，我們知道，對於Riemann常義積分（定積分），可積則絕對可積，反之不對；而對於Riemann廣義積分，絕對可積則可積，反之不對。也就是說，Riemann積分意義下的絕對可積與可積是不等價的。而對於Lebesgue積分，我們知道，可積與絕對可積是一回事，也就是說，絕對可積與可積到了Lebesgue積分的意義下變成了等價關係，Lebesgue積分將絕對可積與可積統一起來。這是Lebesgue積分優於Riemann積分的一個重要區別。
從兩種積分意義下的可積函數類來看，Lebesgue可積函數構成的線性空間是完備的，而Riemann可積函數類不是完備的，也就是說，一個Riemann可積函數列的極限函數可能不再是Riemann可積的，而Lebesgue可積函數類對極限運算是封閉的。這是從函數類上看Lebesgue積分優於Riemann積分的另一個重要特點。
測度論
測度論是屬於實變領域，是在數學當中的分析領域，實變就是實分析 — 顧名思義就是在分析實數空間中的性質（實數與複數空間的差異頗大，所以還有另一個複變領域）。其實基礎的實分析大家都學過，就是大一學的微積分，再進階一點就是數學系的大家口中抱怨的高等微積分，到了研究所就會進入實變函數論。
會有測度論的發展，是因為為了要拓展黎曼積分而開始的。如下圖左所示，黎曼積分是從實軸去分割區間，把分成很多長方形區間來積分，然後在區間中任取一個tk當作長方形的高f(tk)，不過這樣會遇到一個問題：如果在一個區間內f(tk)差很多，這個積分值可能會受到tk取值的影響，故我們說這個函數黎曼不可積。
| 如果我們不要從實軸去分割，而是從函數值分割區間呢？就像圖片一、(右)所看到的，對a這個點去切，蒐集所有函數大於a的集合Ea={x | f(x)>a}，所以塗色面積就會是a | Ea | ， | Ea | 就是我們要去算的集合長度的概念，也可以稱之為測度，因此測度論就展開了。 |
直觀解釋 黎曼 (Riemann) 積分 and 勒貝格 (Lesbegue) 積分
要直觀地解釋兩種積分的原理，可以假設我們要計算一座山在海平面以上的體積。
黎曼積分是相當於把山分為每塊都是一平方米大的方塊，測量每個方塊正中的山的高度。每個方塊的體積約為1x1x高度，因此山的母體積為所有高度的和。
勒貝格積分則是為山畫一張等高線圖，每根等高線之間的高度差為一米。每根等高線內含有的岩石土壤的體積約等於該等高線圈起來的面積乘以其厚度。因此母體積等於所有等高線內面積的和。
佛蘭德（Folland）描述黎曼積分跟勒貝格積分的不同，以非負函數 $ f:[a,b]\mapsto [0,\infty ],\;a.b\in \mathbb {R} $ 這例子來講，黎曼積分是分割 $x$-軸上的定義域區間 為更小的子區間，並計算黎曼和，當子區間越來越小時黎曼和的極限就是黎曼積分；而勒貝格積分則是將 $f$ 在 $y$-軸上的對應域分割成不相交的區間 ${I_{j}}{j=1}^{n}$，並用定義域中的子集合 ${f^{-1}(I{j})=E_{j}}$ 來定義趨近 f 的簡單函數
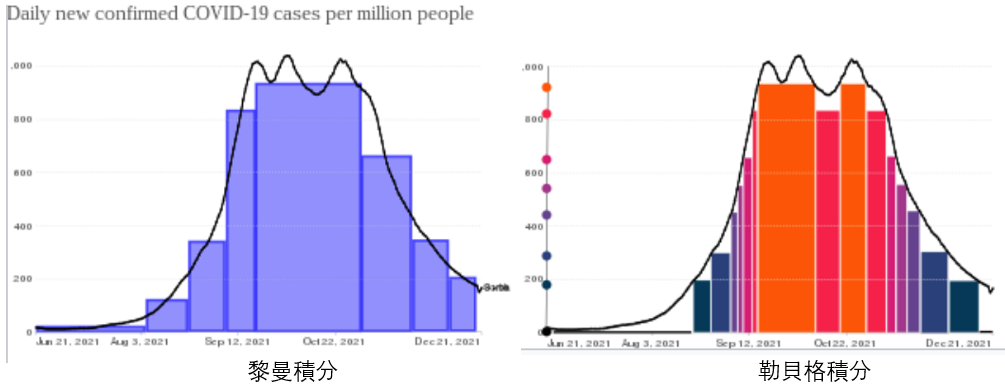
白話就是：黎曼積分是分割定義域來計算積分；勒貝格積分則是用分割值域來計算積分。
- 分割值域有什麽好處? 因爲計算定義域的 “總長度” 或是 ”總面積” 可以用 ”測度理論“。比起分割定義域可能會無法計算個別無窮小定義域的 ”長度” 或是 “面積”。
- 最初測度理論是用來對歐幾里得空間中直線的長度，以及更廣義地，歐幾里得空間的子集的面積和體積進行仔細分析發展出來的。它尤其可以為 $\R$ 的哪些子集擁有長度這個問題提供一個系統性的回答。
- 對於 bouned function $f$ defined on [a,b], if $f$ is Riemann integrable, then $f$ is Lebesgue integrable.
我們看一個例子: 有理數的指示函數 
- 在區間
之間
沒有黎曼積分，因為在實數中有理數和無理數都是稠密的，因此不管怎樣把
- 在區間
是可數集，因此
![\int _{[0,1]}1_{\mathbb {Q} }\,d\mu =\mu (\mathbb {Q} \cap [0,1])=0](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bf52997897b47a982210a92bb1ac615514989bc)
簡單說：勒貝格積分可以處理很多極限的積分。
二、集合介紹
在正式進入測度以前，要先簡單介紹在數學中重要的集合概念。集合顧名思義就是集合了一些元素，在數學中，集合還能分成可數集跟不可數集，意思就是這個集合中的元素能不能用數的，可數集又可以分成有限集與無限集（對你沒看錯，無限集也可以是可數的）。例如，有理數集合為可數集和無限集，無理數集合為不可數集。
當我們把集合的概念放入空間概念中（例如R的N次方空間），就可以定義開集(open)與閉集(closed)。在R的N次方中，開集的定義為：
「*給任意一個屬於集合A的元素a，可以找到一個足夠微小的值ε(>0)，從a延伸出去在距離ε處畫一個圈，如果圈內所有點都落在集合A裡面，則我們稱此集合A為開集合（如下圖二所示）*」。
相反的，若一個集合B的補集是開集合，則B為閉集合。所以我們也可以這樣想，當我們畫一個集合的邊界是虛線時，這個集合八成是開集合；如果有實線邊界，就會是閉集。雖然這樣想不夠嚴謹，但是比較好理解。
開集合有一些性質是必須知道的，比如說：一些（不限多少個）開集合的連集還是開集合，但有限個開集合的交集才會是開集合。相反的，在閉集合方面，根據狄摩根定律（De Morgan law）可以證得，一些（不限多少個）閉集合的交集是閉集合，有限個閉集合的連集還是閉集合。
開集合與閉集合還有很多性質，但那些都屬於高等微積分的內容，在這裡並不會細講。不過還是有兩個重要的集合在之後會提到 — Gδ和 Fσ，Gδ是一些可數個開集合的交集，而Fσ是可數個閉集合的連集。這兩個集合都不會保證是開集或閉集，因為他們不一定有是由有限個集合組成，但開集一定是由某種Gδ，且閉集一定是某種Fσ。看到這裡是不是快暈倒了呢？沒關係，後面看到這些再回來複習就好。
二、外側度
測度（measure）直觀理解上是用來量測一個集合的大小。例如，在一維的實數空間中，測度就是指集合的長度；在二維平面中，測度可以想成集合的面積，以此類推，三維空間中測度就有種體積的意義。當然，我們探討的空間可以到n維，所以必須要給測度一個更明確的定義。
不過，不是每個集合都是可以測量的（之後會提到不可測量的集合），所以在定義測度之前，要先定義了外測度(outer measure)，而這個外測度是對於所有集合都有的，就像有些函數無法做黎曼積分時，會使用上積分跟下積分來定義他的範圍的概念一樣。外測度的定義如下：
定義的意思為，對於集合E，可以被一些可數個區間Ik蓋住（covering），把這些區間蒐集成集合S（不同的covering就會有不同的S），而外測度就是指這些Ik體積總和的最大下界（就是最小可以到多小的意思），如圖三所示。也就是說，我們可以把外測度想成是在集合外面包了包裝紙，然後外測度是算包裝紙的大小，且盡量讓包裝越小越好
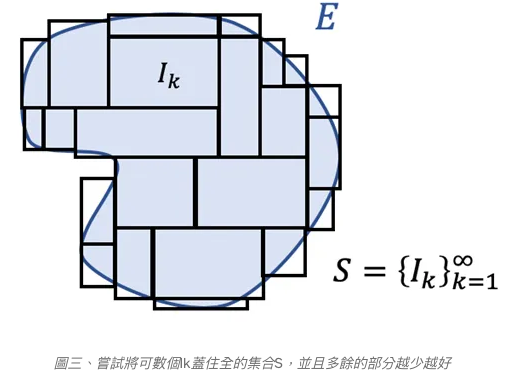
在定義了外測度之後，有一些定理跟性質是值得一提的。比如，如果集合E可以寫成可數個Ek的連集，那麼E的外測度會小於等於所有Ek外測度的總和，這應該是一個很直觀的定理（由廣義三角不等式）。
如果集合中只有單點(例：Ek ={ p } )，由外測度的定義可以很直觀地知道，包覆住單點的外包裝的大小可以一直縮小，所以單點的外測度是0。所以依照上面所提的定理，如果E為有理數集，則他的外測度也會是0，因為有理數集是由可數個單點所組成，把每個Ek當成有理數單點，所有Ek外測度的總和為0，所以E的外測度≤0且外測度不會是負數（僅限在此所介紹的），有理數集的外測度是0。
三、可測集、測度0
在了解外測度的定義之後，就可以真正的進入測度了。測度的定義一定要跟外測度有關，如果無關，那他們就會具有不同的意義。直接來說，如果一個集合是可測的，那麽就定義外測度就等於測度值。重點是，我們就是不知道怎麼樣的集合叫可測集呀？但如果我們目的是要讓可測集的外測度等於測度值，就要像我們剛剛所比喻的，集合的外包裝要越緊貼集合越好，也就是集合跟外包裝要幾乎沒有空隙才行。
帶著這樣的想法，我們就可以更透徹的理解可測集的定義（定義(1)）。如果我們說一個集合E是可測的，那麽對於任意小的正數ε，可以找到包含E的開集合G（外包裝），然後G扣掉E的外測度要小於ε，就如圖四、(左)所示，灰色集合要很小的意思。
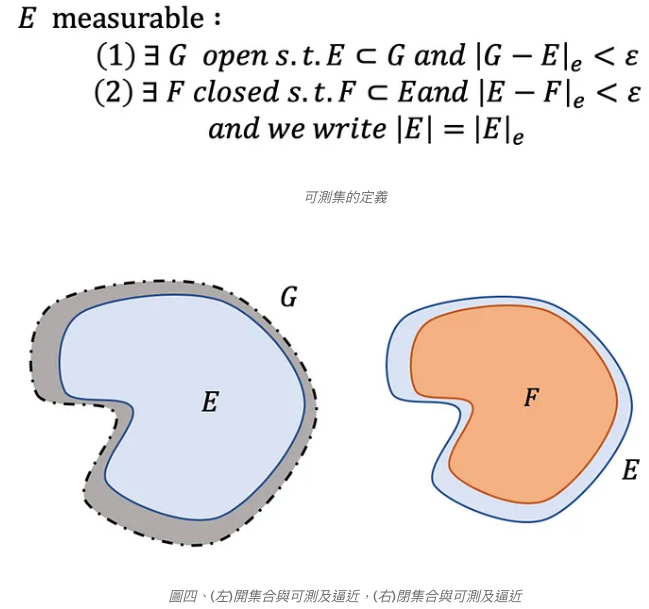
其實可測集也有一個等價的定義（定義(2)）。想像一個集合也需要內包裝，那麼也是希望內包裝能夠跟集合越貼近好，所以另一個等價的定義如下：如果集合E是可測的，那麽對於任意小的正數ε，可以找到一個比E小的閉集合F（內包裝），然後E扣掉F的外測度要小於ε，就如圖四、(右)所示，藍色集合要很小的意思。
知道測度定義之後，就可以知道哪些集合是可測的。例如，開集合、閉集合、可數個可測集的連集或交集、可測集的補集⋯等（這些都可以證明），值得一提的是外測度0的集合也是可測集。這些外測度為0的可測集，因為定義外測度等於測度，所以我們也可以說他們是測度0或0測度(measure zero)。測度0在直觀上代表著那些不佔體積的集合。在一維實數空間中，測度0可以是單點，或是可數個單點；在二維空間中，直線是測度0；所以類推，在n維實數空間中，能用n-1維表示的集合都可以是測度0。
四、不可測集
上一段落說了，很多集合都是可測集，那值得疑問的是，真的有不可測集存在嗎？
義大利數學家維塔利(Vitali)就證明出存在不可測集合(non-measurable set)。在尋找的過程中，用了選擇公設跟一個定理。首先，他先定義了「*一個集合Ex為蒐集所有與x的距離是有理數的點」*，Ey為相同定義，則Ex、Ey兩集合不是全等就是不相交的集合。如果他們兩有交於至少一個點，令此點為x1，依照集合定義，x點距離x1、y點距離x1都是有理數，所以x-y也是有理數，所以y會在Ex中，故Ex、Ey兩集合會全等，如圖五所示。
六、Lebesgue 積分 vs Riemann 積分
介紹了這麼多，終於到我們這篇的重點：Lebesgue 積分。Lebesgue 積分的發展是為了要解決黎曼積分受到的限制。當一個函數不連續點夠多時，黎曼積分可能不存在，以下舉個例子來具體解釋黎曼積分的限制。
令Dirichlet 函數為：
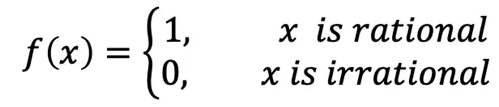
此函數大家在微積分應該都略有所聞，是一個處處不連續的函數。當我們定義這個函數在[0,1]區間裡，在這個區間做黎曼積分的話是不可積的。因為根據黎曼積分的定義：
| R(f,E)的意思是蒐集f函數以下的所有點當作這個集合，所以如果定義x在一維空間的話，那就是蒐集f函數與x軸中間的面積，其實跟一般積分的意思差不多，只是這邊用測度來表示而已( | ． | n+1 是在R^(n+1)裡取測度的意思)。在這個定義之下，假設f是非負函數且定義在可測集合E，此時有另一個定理說，如果f是可測函數的話，則f在E上為Lebesgue可積。 |
現在知道了Lebesgue可積的定義，就可以知道黎曼積分跟Lebesgue 積分差在哪裡了。還是以Dirichlet 函數為例，如果要對Dirichlet 函數做 Lebesgue 積分，則會運用到以下這個定理：
令g=0在[0,1]區間上，又根據我們有提過有理數集合是0測度，所以f≠g 的點其實是0測度（f只在有理數點上不等於0），所以幾乎處處f=g。依據這個定理，此時Dirichlet 函數為Lebesgue可積，且f的Lebesgue 積分=g的Lebesgue 積分=0。由此可見Lebesgue成功的把黎曼積分的限制推廣出去了。
Reference
Lebesgue integral
https://en.wikipedia.org/wiki/Lebesgue_integration @wikiLebesgueIntegration2023: Lebesgue 積分英文
https://zh.wikipedia.org/zh-tw/%E5%8B%92%E8%B2%9D%E6%A0%BC%E7%A9%8D%E5%88%86 : 中文
@shionStochasticDynamic2021
https://zhuanlan.zhihu.com/p/343129740
[@ccOneArticle23]. https://zhuanlan.zhihu.com/p/589106222 very good article!!! SDE for diffusion score
https://yrgnthu.medium.com/%E5%AF%A6%E8%AE%8A%E7%9C%9F%E7%9A%84%E8%A6%81%E8%AE%80%E5%8D%81%E9%81%8D-%E5%8D%81%E5%88%86%E9%90%98%E5%B8%B6%E4%BD%A0%E4%BA%86%E8%A7%A3%E6%B8%AC%E5%BA%A6%E8%AB%96-f5a79c9cf5a7
[@yangRealAnalysis2022]