https://www.youtube.com/watch?v=cEEahoUUGyc
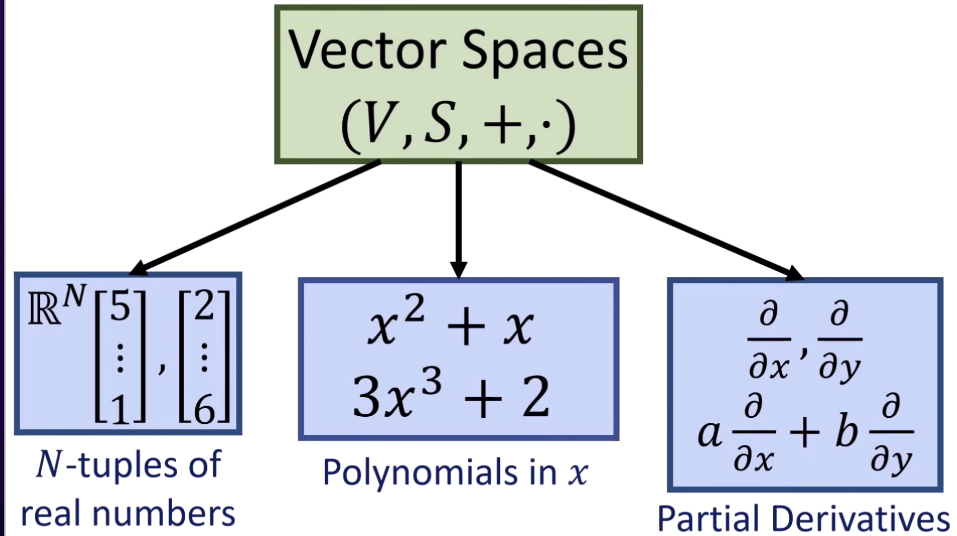
Vector Space Abstraction
Key message: covariant derivative (or connection) 是一種 vector space.
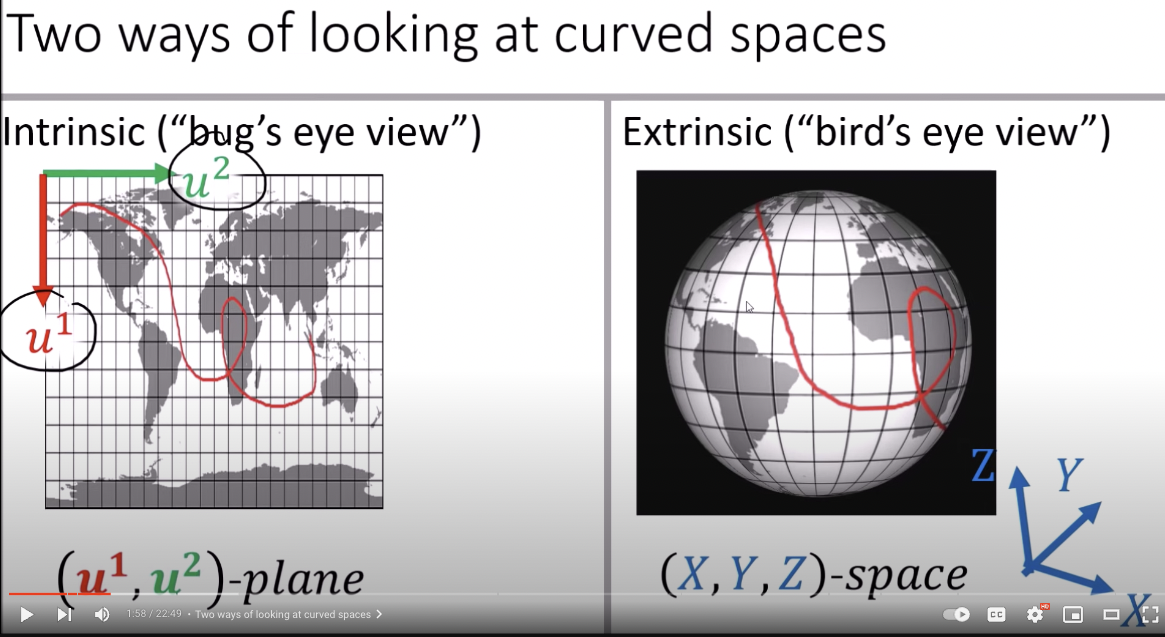
Two Views
Covariant derivative (extrinsic view with normal component subtracted): Bird-Eye-View (BEV)
Intrinsic view (Bug-Eye-View) BEV ??!


Geodesic 就是第一項為 0.

Intrinsic 用球面為例
External View
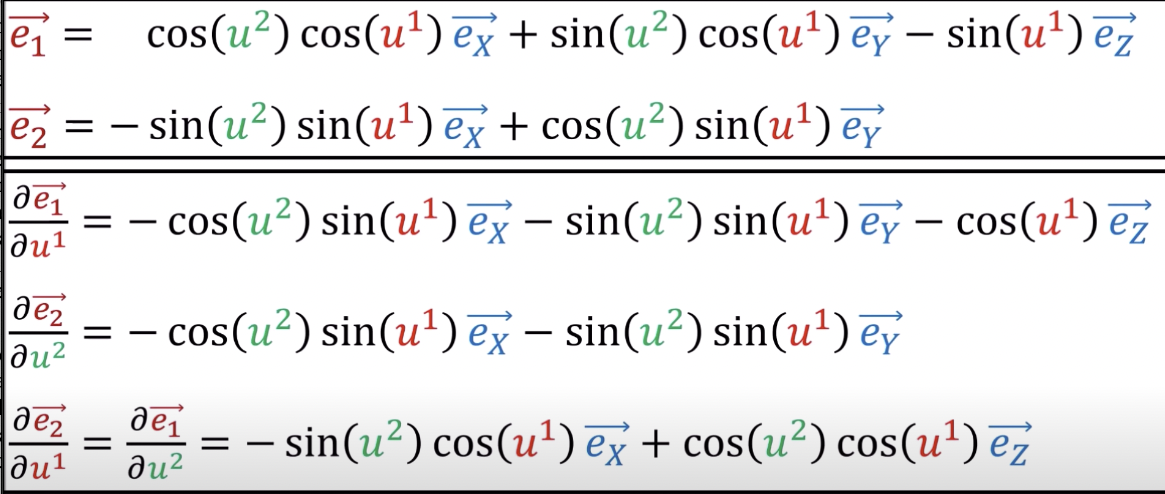
For Intrinsic View : No more global x,y,z (use u, v), no global origin, no position vectors, R
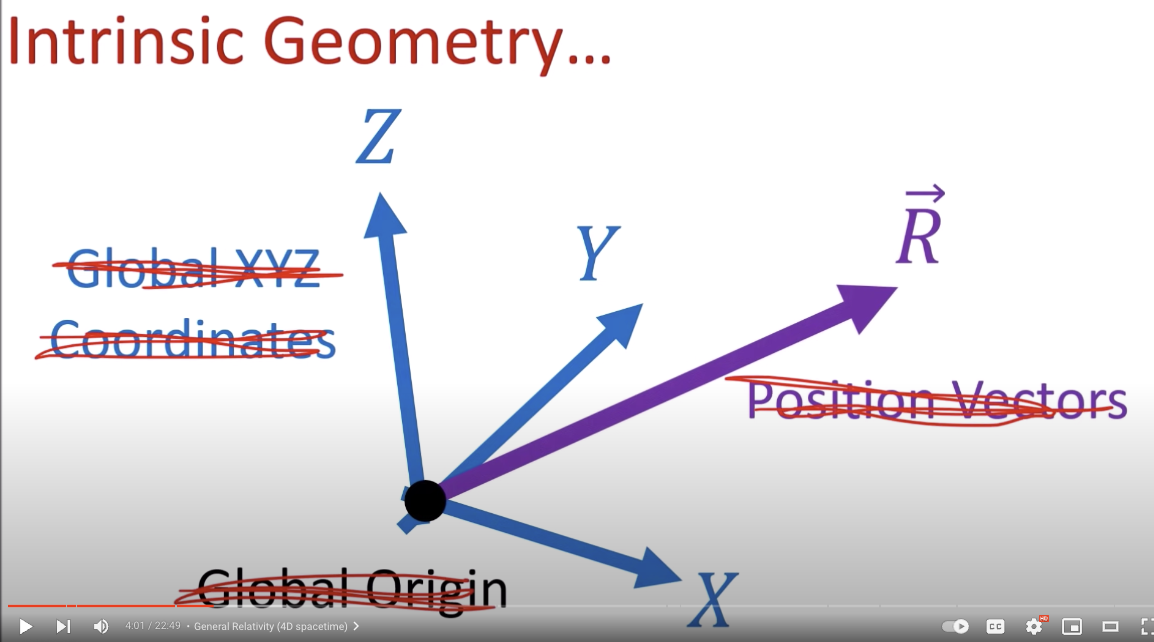
而是:
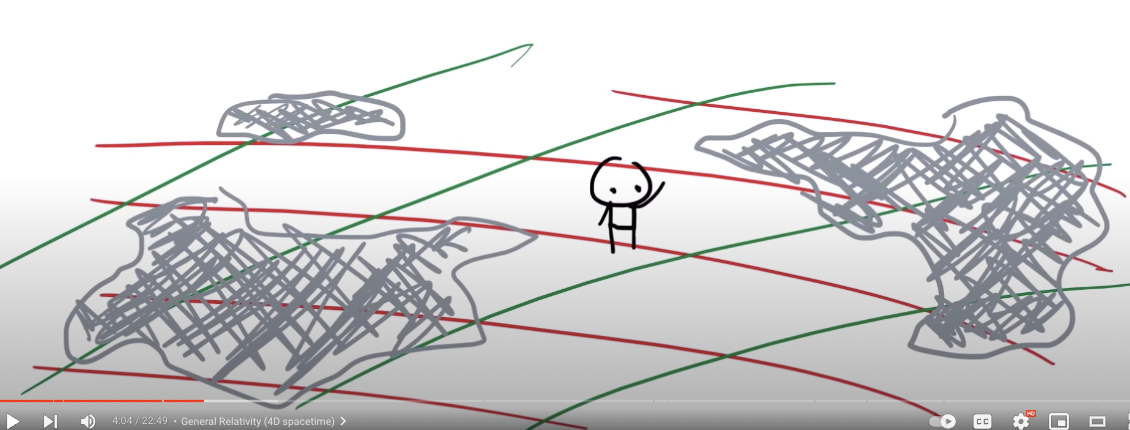

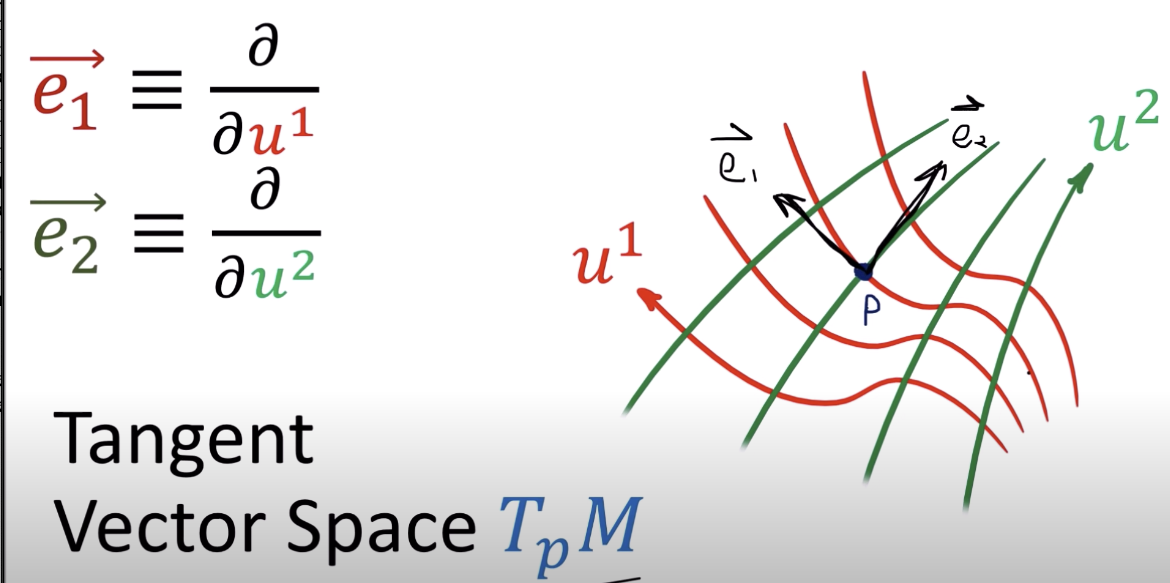
Covariant Derivative

沒有 normal vector, just ignore!
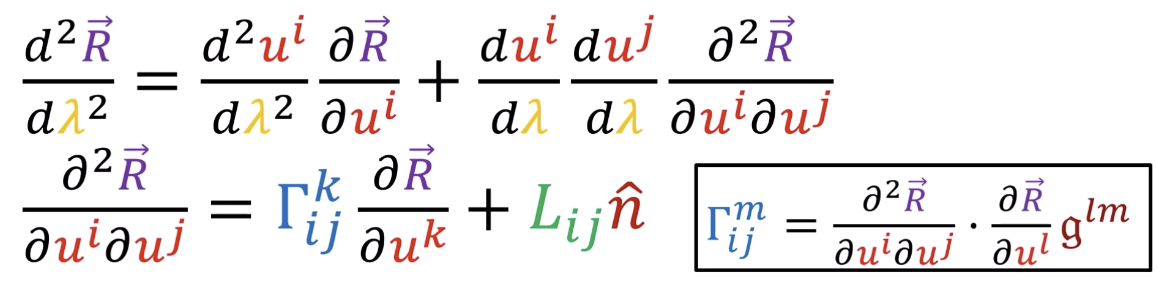
Need a new strategy to compute Christoffel symbol!!
In intrsinc geometry, metric tensor needs to be given!!
如果是已知的 manifold, 可以直接計算 metric tensor (from external view).
如果是廣義相對論或其他物理,metric tensor 可以猜出來,or from God.
只要給定 metric tensor, 可以計算 (Intrinsic) Christoffel symbol, 以及 (intrinsic) curvature.
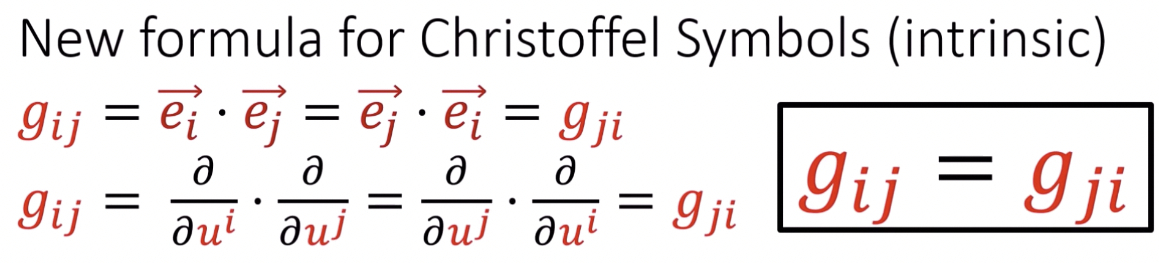

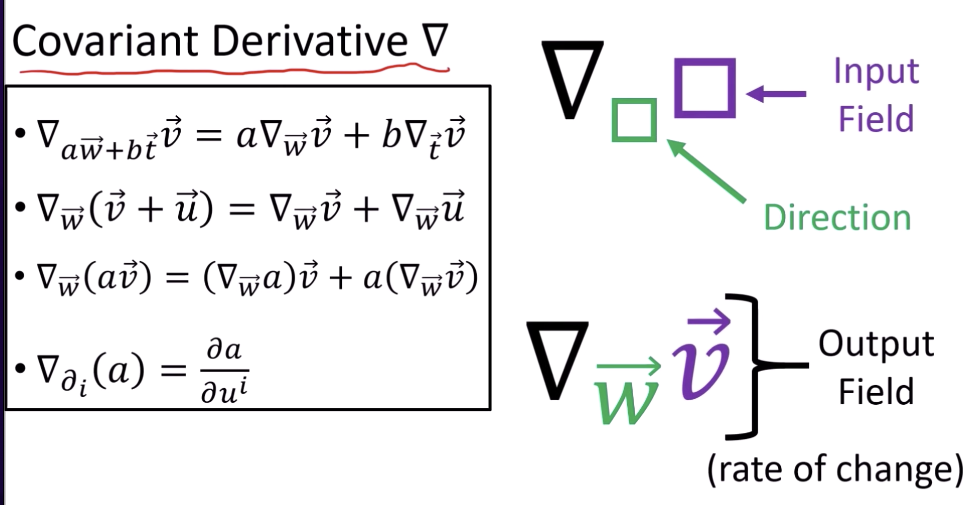
Connection = Covariant Derivative
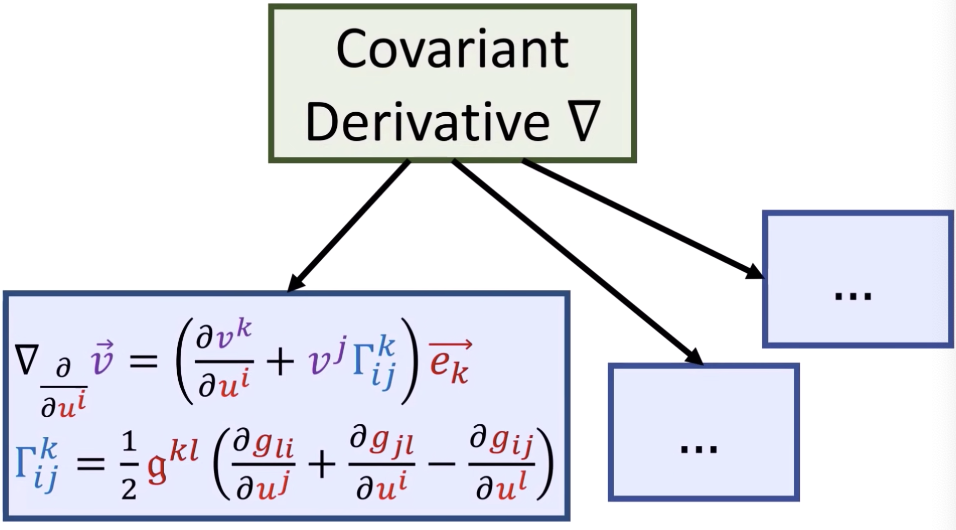

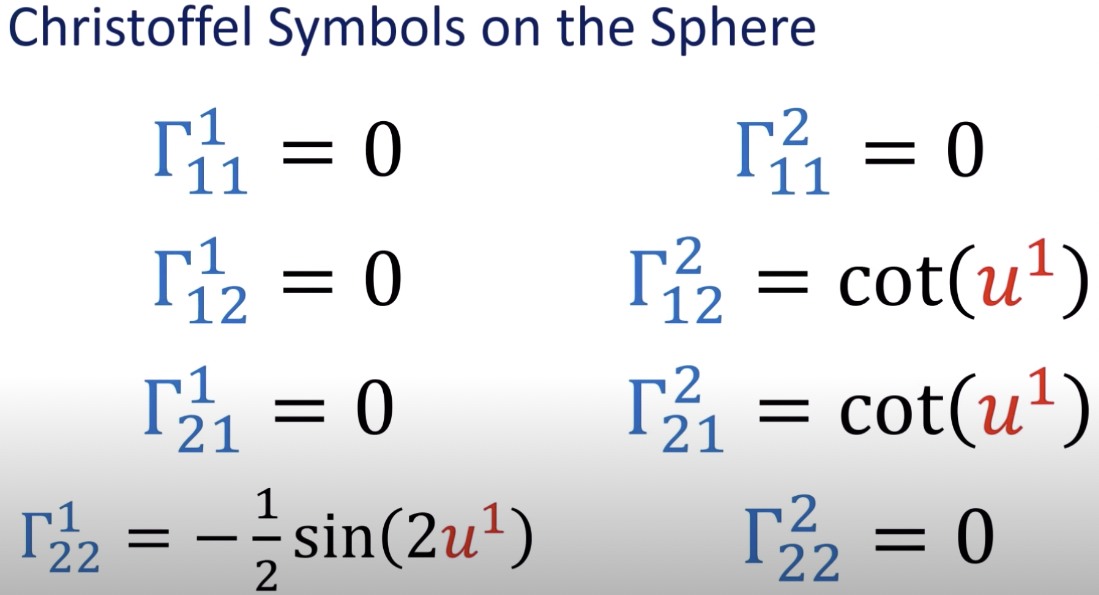


- Directional derivative 一般只是 on scalar function/field (i.e. gradient). 可以擴展到 vector function/field 就是 covariant derivative!
- Directional derivative on scalar field 就是梯度,是 covariant! 所以擴展到 vector field 的 covariant derivative 也是 covariant!
- 下面 1, 2 式 a, b是常數。3, 4 f 是 scalar field. 滿足 vector space 的定義。
- \[\begin{aligned} & \nabla_{a \vec{w}+b \vec{t}} \vec{v}=a \nabla_{\vec{w}} \vec{v}+b \nabla_{\vec{t}} \vec{v} \\ & \nabla_{\vec{w}}(\vec{v}+\vec{u})=\nabla_{\vec{w}} \vec{v}+\nabla_{\vec{w}} \vec{u} \\ & \nabla_{\vec{w}}(f \vec{v})=\left(\nabla_{\vec{w}} f\right) \vec{v}+f\left(\nabla_{\vec{w}} \vec{v}\right) \\ & \nabla_{\partial_i}(f)=\frac{\partial f}{\partial u^i} \end{aligned}\]

##