Reference
https://github.com/kenjihiranabe/The-Art-of-Linear-Algebra The Art of Linear Algebra: good reference
矩陣分解
前文提到方陣的特徵值分解 (EVD)和矩陣的奇異值分解 (SVD) 是兩個極其重要而又相關的分解。
最重要結論:
-
特徵向量 (Eigen vector) **描述的是矩陣的方向 (座標系) **不變作用 (invariant action) 的向量;
-
奇異向量 (Single vector) 描述的是矩陣最大作用 (maximum action) 或是保持正交的方向向量。
EVD 和 SVD 在矩陣是對稱方陣基本相同,唯一的差別是特徵值可正可負,但是奇異值一定是正值。所以 EVD 和 SVD 可以差個 (-1).
我們知道除了 EVD 和 SVD 還有很多的矩陣分解方法,如下圖。
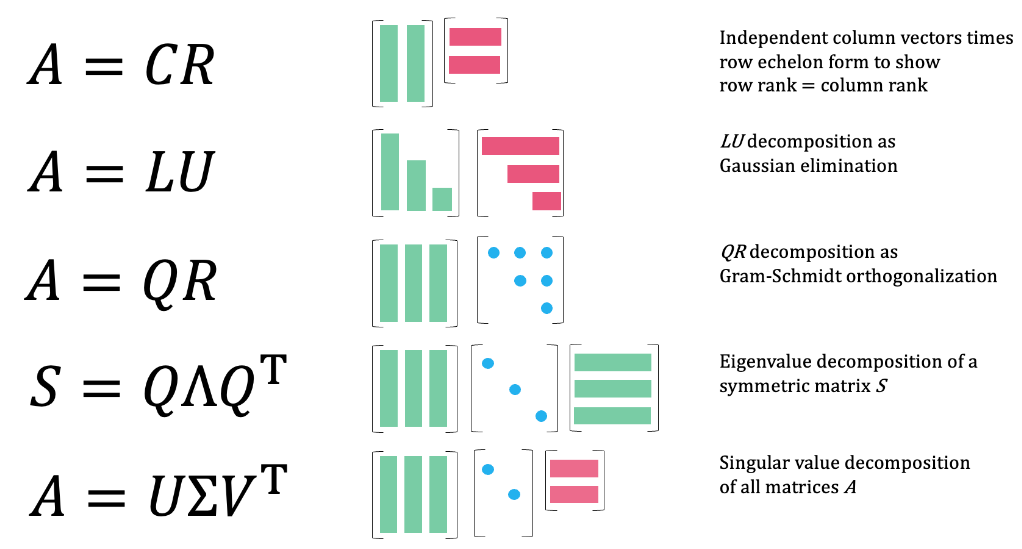
矩陣 (Matrix)
-
奇異值分解是矩陣 ($m \times n$) 最重要的分解方式。$A = U \Sigma V^T$.
- $U$ 是 $m \times m$ 的正交方陣,$V$ 是 $n \times n$ 的正交方陣,$\Sigma$ 是 $m \times n$ 的類對角矩陣。
- 物理意義是先旋轉 $V$ 的角度,再根據 $\Sigma$ 的奇異值 scale,最後再旋轉 $U$ 的角度。
- 例:A = [1, 2, 3; 4, 5, 6] m = 2, n = 3.
方陣 (Squre Matrix)
對於方陣,第一個重要的特性就是是否可逆。從代數的角度來説,就是是否能做加減乘除中的除法。關係到聯立方程式求解,或是可以做很多信號處理 (equalization, Kalman filter, etc.)。
判斷方陣是否可逆有很多方法,例如 det(A) 是否為 0, 或是奇異值是否為 0, 或是特徵值是否為 0.
- 可逆方陣是我們喜歡的方陣,因爲可逆所以可解聯立方程式。
- 三角分解:可用 QR 三角分解,得到聯立方程式的解。同時得到正交基底 (Gram-Schmidt)。
- 逆方陣:$A^{-1} = V \Sigma^{-1} U^T$. 從物理角度很自然,就是反向操作,加上奇異值 scaling 的部分變成倒數。
- $A A^{-1} = U \Sigma V^T V \Sigma^{-1} U^T = I $
- 如果方陣不可逆:det(A) = 0 或是至少有一個特徵值或奇異值為 0
- 可用 LU 三角分解。L: lower; U: upper. U 至少有一列為 0
- 因爲可逆非常有用,所以我們可以定義 pesudo-inverse. 想法很簡單,就是利用上述公式再修改。
- 僞逆方陣 $A^{+} = V \Sigma^{+} U^T$, $\Sigma^{+}$ 就是非 0 奇異值的倒數 (跳過 0).
- (注意) $A A^{+} = U \Sigma V^T V \Sigma^{+} U^T = I$。 不可逆方陣存在(無窮)方陣和原方陣的積為 $I$. 僞逆方陣是其中之一。把 $\Sigma^{+}$ 奇異值為 0 改成任意值都可以得到乘積為 $I$.
可對角化方陣 (Diagonalizable Matrix)
接下來都是特徵值分解的天下
一般可逆方陣都是可對角化方陣,特指特徵值分解的對角化方陣。但特徵值分解不保證一定是實數。此處是指特徵值為實數的對角化方陣 (?)。
- $A = X \Lambda X^{-1}$
如何保證 $A$ 的特徵值為實數?一個方法是對稱方陣。不過可以放寬一點,就是 normal matrix.
- Normal matrix : $A^T A = A A^T$. 對稱方陣 $A = A^T$ 一定是 normal matrix,反之不爲真
- 如何證明 normal matrix 一定是 diagonalizable matrix?
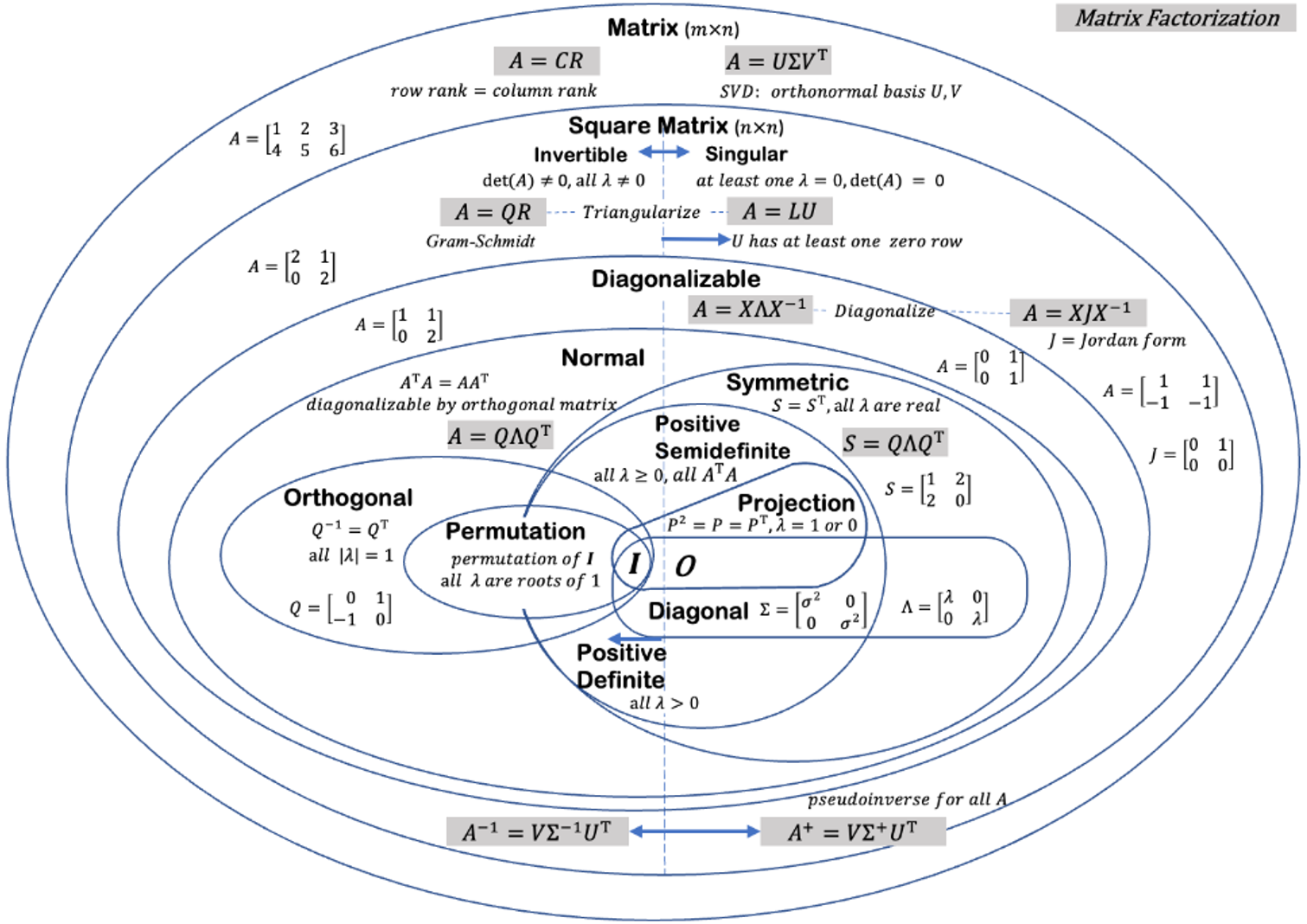
對稱方陣 (King of Matrix)
此處就不再多做説明。
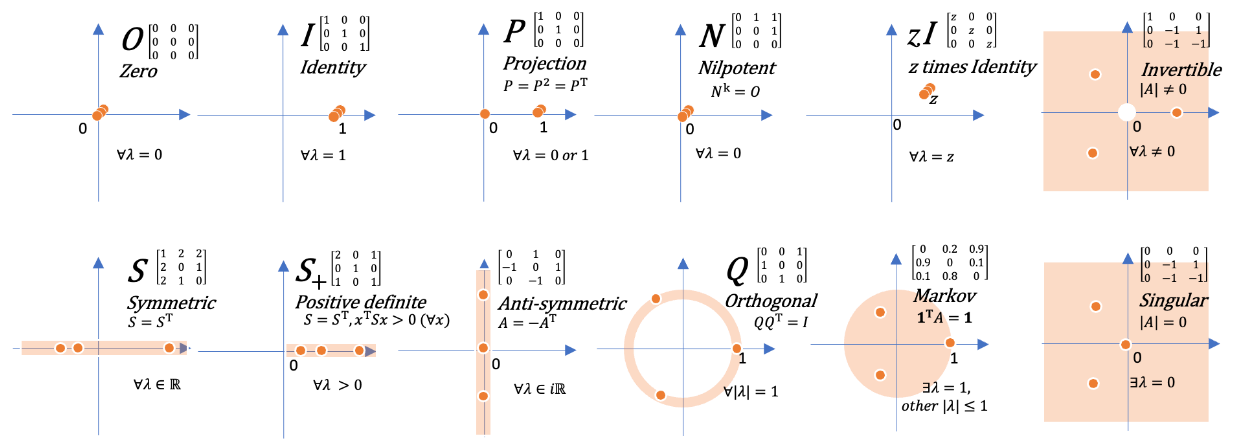
$n \times n$ 方陣特徵值地圖
接下來就聚焦在 diagonlizable matrix, 使用特徵值分解。
- Projection matrix 的特徵值是 1 and (1個) 0.
- 對稱方陣的特徵值是實屬.
- Positive definite 特徵值是正數.
- Orthogonal matrix: 特徵值絕對值為 1.
- Markov matrix: 特徵值 1 個為 1,其他特徵值的絕對值小於 1, 所以會收斂。
##