平行公理和平行移動 Parallel Postulate and Parallel Transport

Posted on | In

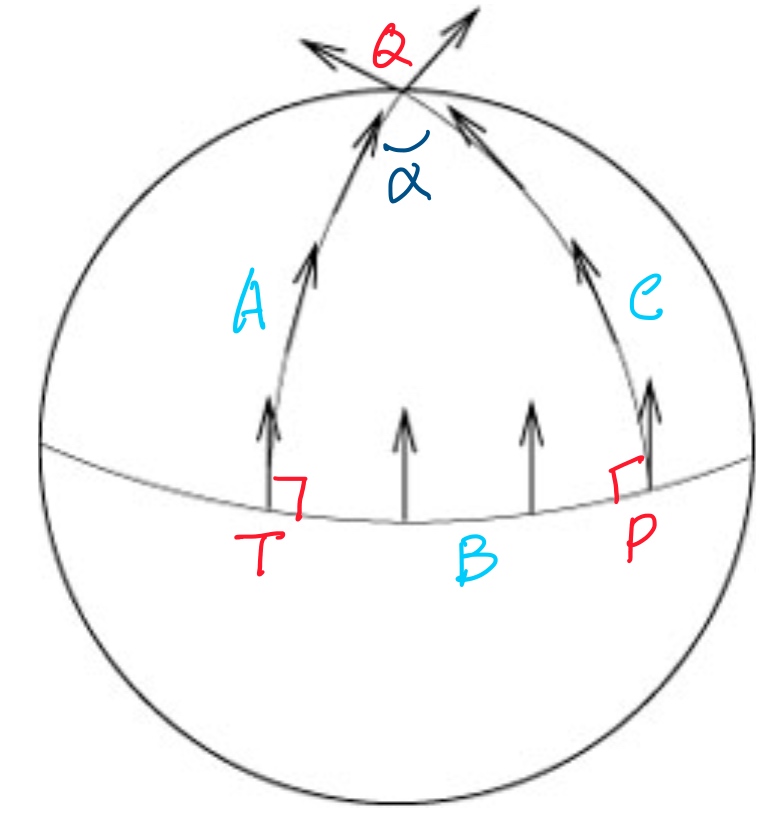
Source

http://wordpress.discretization.de/geometryprocessingandapplicationsws19/connections-and-parallel-transport/. Connection and Parallel Transport

Math 302 Parallel Postulates

file:///Users/allenlu/Downloads/9781429799850-14.pdf link parallel transport with parallel postulate

Introduction

人類是視覺的動物，我們是如此習慣 global view 對於一些 global view take for granted.

例如：直線，平行，… 都是一眼可以看出來，但是定義起來要花一些思考。如何轉換的曲面就要小心。

直線：兩點間最短的路徑 -> 可以直接推廣到曲面。

平行：兩條直線永遠不相交。或是兩條直線之間等距離。這兩者在平面等價，但在曲面不是。例如北緯 10 度線和赤道是等距離也不相交。但是北緯 10 度線不是曲面的直線（大圓）！但是赤道是曲面的直線（大圓）。

就像我們如此習慣 10 進位因為有 10 隻手指頭。對於轉換到 2 進位，8 進位，16 進位需要大腦的 extra-time to process.

所以直線，平行線還有用嗎？ Yes!! 非常有用，但是 go local, 就是 parallel transport.

幾何根據全域或局部以及外視或内視可以略分為 4 類：

  • Local (局部): 基於非常小區域 (微分=無窮小) 的特性，例如曲率 (curvature)、connection (covariant derivative)

  • Global (全域): 基於 loop、transversal (軌跡)、大區域的特性，例如圓周率、三角形内角和、曲面的形狀
  • Extrinsic view (外視): birds-eye-view (上帝視角) 即是 manifold 是嵌入更高維的歐式空間 (X, Y, Z 卡氏座標)
  • Intrinsic view (內視): bugs-eye-view (毛毛蟲視角) 沒有參照坐標系，只能靠 manifold 本身的 objects (綫，角度，平行移動) 推導 manifold 的性質。結果應該和 extrinsic view 結果一致。

一個的例子説明不同的方式定義“平行”。

平行 Extrinsic (Birds-Eye-View) Intrinsic (Bugs-Eye-View)
Global (大區域) 兩條直綫不相交，修改平行公理 (HSP) 沿著軌跡的平行移動
Local (非常小區域，微分) 局部平行移動: 忽略 normal 分量 局部平行移動: connection, curvature

image-20230708180217026

平行公理

什麽是平行綫？這是小學生的問題: (1) 兩條直線 (2) 永遠不相交稱為平行線

歐幾里得把平行線公理化，稱爲第五公理。

  • Euclid‘s 5th Postulate (EFP): 一條直綫 $l$ 與其他兩條直綫 $m$ 和 $m’$ 相交，且這些線段在 $l$ 的同側所形成的內角之和小於180度，則線段 m 和 m’ 將會在該側的某一點相交。

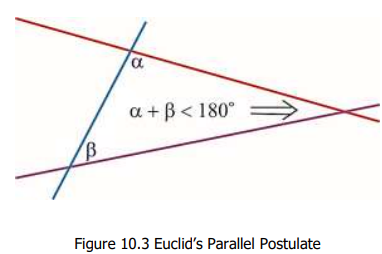
image-20230711141730219

我們在高中學的是改良後的公理。

  • High School Parallel Postulate (HSP): 一條直綫 $l$ 與綫外一點 $P$，存在唯一的直綫 $l’$ 通過 $P$ 和 $l$ 平行不相交。

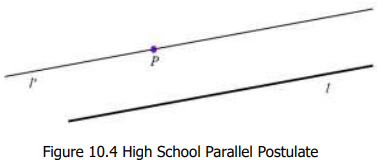
image-20230711141757767

乍看很直觀，但有幾個問題

  1. 什麼是直線
  2. 什麼是“永遠”不相交？還是相交在無限遠？數學家不喜歡沒有清楚的定義：永遠、極限、無限大/遠等等。
  3. HSP 只存在一條直綫和原來直綫平行不相交？可以有無限條 (平行?) 直綫不相交，或是沒有任何 (平行?) 直綫不相交？

非歐幾何

Lobachevsky (羅巴切夫斯基) 和 Riemann (黎曼) 修改 HSP 開創非歐幾何學：羅氏幾何學是雙曲幾何，有無限條直綫不相交；黎曼幾何學則是橢圓幾何，不存在直綫不相交。

事實上，我們可以用三角形內角和大於/等於/小於 180 度判斷是橢圓/平面/雙曲幾何學，或是用圓的面積除以周長大於/等於/小於 $\pi$ 判斷是橢圓/平面/雙曲幾何學。

如此 (全域) 平行線的觀念還有用嗎？是的，非常有用，不過要轉成 (局部) parallel transport (PT) 的定義。

In summary, Parallel Transport (PT) 是局部 (local) 的平行定義，可以拓展到全域 (global) 平行定義。

注意 parallel transport 可以有外視 (extrinsic view) 或是内視 (intrinsic view).

  • Holonomy (H=0 for 平面): 和樂? parallel transport 在經過一個完整 loop 的角度變化。
  • (PT!) Independence of Parallel Transport: If two lines are parallel transports (PT) along one path (or transversal) then they are PT along ALL paths (transversals).

Connection = Covariant Derivative

Covariant derivative 是 directional derivative 的延伸！

  • Directional derivative 是作用在 scalar field 上
  • Covariant derivative 是做用在 vector field 上

平行移動物理意義

Parallel Transport $\vec{V}$ 沿著一條線(不需要直線 or geodesic) $\vec{r}(\lambda)$ 的局部變化為 $\vec{0}$, $\lambda$ 是參數 normalized to 弧長，所以和座標系無關。

image-20230709165740972

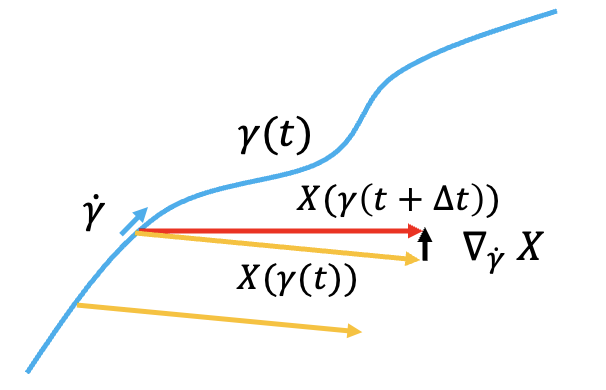
image-20230709181902211

  • Parallel transport 的定義就是在 $\gamma(t)$ 的切向量方向的 covariant derivative 為 0. 什麼是 covariant derivative, 就是 $X$ (向量) 對 $\gamma$ 位置的微分如上圖。可以想像是 $X$ 是一根棍子指向一個方向， covariant derivative 是這個方向隨 $\gamma$ 移動的法向偏移。
    • Covariant derivative 包含 $X$ 本身隨位置的變化加上座標系本身隨位置的變化 (Christoffel symbol)。所以 parallel transport $X$ (向量) 是和 curve $\gamma$ 相關。
  • 但在平面是個特例，基本所有的“平行線/向量”在任何的 smooth $\gamma(t)$ 都是 parallel transport. 也就是 parallel transport 和 $\gamma(t)$ 無關！ independence of transversals (!PT)
    • 平面的 Christoffel symbol = 0，covariant derivative 就和 directional derivative 一樣。 \(\begin{aligned}& \nabla_{\frac{\partial}{\partial u^i}} \vec{v}=\left(\frac{\partial v^k}{\partial u^i}+v^j \Gamma_{i j}^k\right) \overrightarrow{e_k} \\& \Gamma_{i j}^k=\frac{1}{2} \mathrm{~g}^{k l}\left(\frac{\partial g_{li}}{\partial u^j}+\frac{\partial g_{lj}}{\partial u^i}-\frac{\partial g_{ij}}{\partial u^l}\right) \\&\end{aligned}\)
  • 但是在曲面上，例如球面，因為座標系隨位置變化 (Christoffel symbol), parallel transport 直接和 curve 相關。如下圖。在北緯 20 度線的 parallel transport 就隨著位置改變！

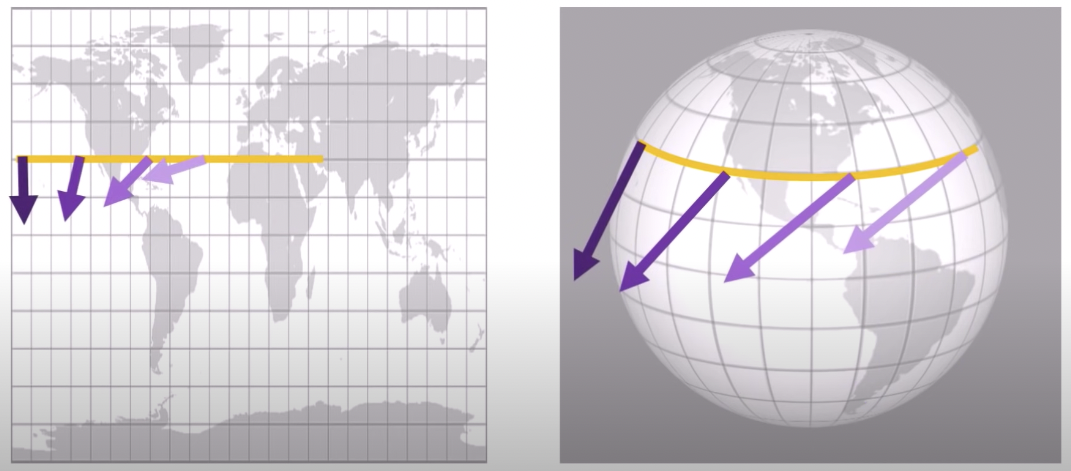
image-20230709210511127

  • 當然如果是在赤道上，parallel transport 看起來就好像指像同一個方向。下面的 link 提供互動的介面。

image-20230709185131445

平行移動的數學表示

Parallel Transport $\vec{V}$ 沿著一條線(不需要直線 or geodesic) $\vec{r}(\lambda)$ 的局部變化為 $\vec{0}$, $\lambda$ 是參數 normalized to 弧長，所以和座標系無關。

Parallel transport 更數學而且和座標系無關的定義：$\vec{V}$ 在 $\vec{r}(\lambda)$ 切線 $\vec{u}$ 的方向導數（微分）為 $\vec{0}$. (注意向量場的所有 basis 方向的導數是張量，某個特定方向, $\vec{u}$, 的導數是向量，也就是“affine connection”. 在曲面空間稱為 Levi-Civita connection.)

\[\nabla_{\vec{u}} \vec{V} = \vec{u}\cdot\nabla\vec{V} = \vec{0} \quad \text{where}\quad \vec{u} = \frac{d\vec{r}}{d\lambda}\]

一個類比：如果不是一個向量 $\vec{V}$, 而是一個純量 $\phi$ 滿足下式。(注意純量場的所有 basis 方向的導數是向量，稱為梯度 gradient. 某個特定方向, $\vec{u}$, 的導數是純量。）$\vec{r}$ 就是等高線或等位線。

\[\nabla_{\vec{u}} \phi = \vec{u}\cdot\nabla\phi = 0 \quad \text{where}\quad \vec{u} = \frac{d\vec{r}}{d\lambda}\]

平行移動和等高線的數學公式雖然非常類似。問題的形式 (formulation) 卻不同。 平行移動是給定一條任意線 $\vec{r}(\lambda)$（open or close) 以及一點 $P$ 的 vector $\vec{V}(P)$, 用 (1) 找出沿線所有點平行移動的 $\vec{V}$. 等高線是給定一個純量場 $\phi$ 以及任一點 $P$, 用 (2) 找出通過 $P$ 的等位線 $\vec{r}(\lambda)$（open or close).

Holonomy (平行移動沿著 close loop 的夾角)

Holonomy 把 parallel transport 結合 close loop， 如下圖綠色軌跡。就是 parallel transport 沿著任意 (逆時針方向) close loop 回到原來的位置的角度變化。

  • 如果是平面幾何：holonomy $H = 0$.
  • 如果是橢圓幾何：holonomy $H > 0$ (parallel transport 逆時針方向角度和 holonomy 軌跡同向)。
  • 如果是雙曲幾何，holonomy $H < 0$ (parallel transport 順時針方向角度和 holonomy 軌跡反向)。

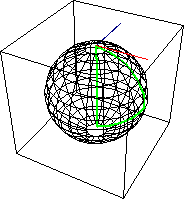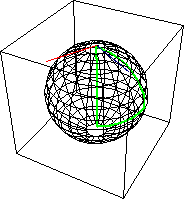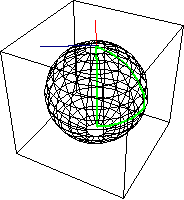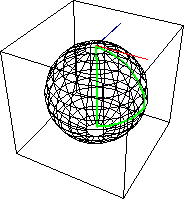
Holonomy group

從 holonomy 為 0 或不爲 0 可以得到兩個結論

  1. (Global and intrinsic view) 如果任意 holonomy 為 0，$H=0$，對應平面幾何 $\to$ !PT 成立，説明如下。

  • 因爲任意 Holonomy 可以分解成兩個任意 paths ($A \to B$)：parallel transport 在一個 path $A\to B$，也會是其他所有 paths 的 parallel transport. 這稱爲 independence of parallel transport 或者 !PT，也就是 $H=0 \equiv \text{ !PT }$

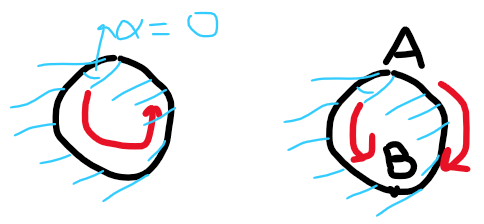
    image-20230712165645222

  1. (Global and intrinsic view) 如果 holonomy 不爲 0 ($H = \alpha \ne 0$)，對應非歐幾何$\to$ !PT 不成立

  • 如果是一個 close loop (沒有交叉) 如下圖左一和左二。Parallel transport 在左邊 path $A\to B$，和右邊 path $A\to B$ 顯然會差 $\alpha$ 角度。所以 !PT 不成立。

  • 但是否有 path 會讓 $A \to B$ 的 parallel transport 相等？Yes , 如下圖兩條相交的 paths, 如果安排巧妙，兩者 parallel transport 相減 等價於兩個 close loops of 相反方向。如果安排巧妙可以互相抵消。因此兩個 paths 的 parallel transport 為 0。不過這是例外的特例。

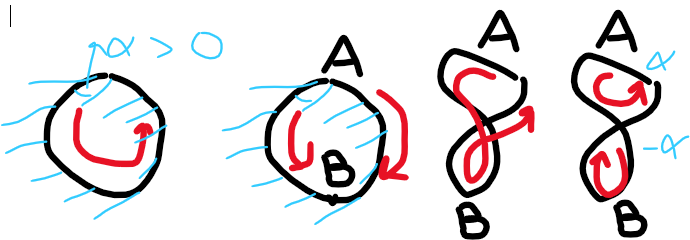
    image-20230712171902764

  1. (Local and intrinsic view) 使用無窮小 (微分) holonomy 定義曲率 (curvature) 如下圖：

    • 對 holonomy loop 的 parallel transport 可以變成兩個 paths 的 parallel transport $\vec{V}$相減，如下圖。當 path ($\beta \to \gamma$ 和 $\gamma \to \beta$) 變成無窮小，並且除以 $\Delta \beta, \Delta \gamma$。也就是：${\left[\nabla_\gamma \nabla_\beta-\nabla_\beta \nabla_\gamma\right] V_\alpha} $

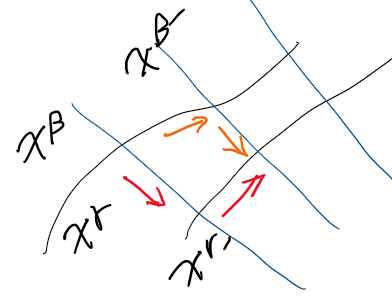
    image-20230713143821786

平面和曲面幾何的 Holonomy

平面幾何：平行移動先定義 Geodesic A, 接著線外一點 P, 可以找到一條 Geodesic B 垂直於 A at T. 再來根據平行公理，只有一條平行線 Geodesic C 平行於 A, 且垂直於 B. 因為 A 和 C 是平行線，永不相交。為了讓 parallel transport 形成封閉迴路 (holonomy), 可以在 A 上找一點 Q, 並且做垂直線到 C， 稱為 geodesic D. 此時從 $A_P$ 的切線，一路到 $A_Q$ 都是 parallel transport. 和 $A_P$ 經由 $B \to C \to D \to A_P$ 的 parallel transport vector 會是平行。也就是夾角為 0！這是一個 trivial case. 沿著長方形兩邊是切向量，兩邊是垂直向量的 holonomy, 在 close loop 的夾角為 0.

柱面幾何：直接剖面切開就是平面。parallel transport 和平面一樣。如果沿著三角形 holonomy, 因為內角和為 180, 回到起點的 parallel transport 夾角為 0. Gauss curvature 為 0.

錐面幾何：圓錐面如下圖(a)的曲率？圓錐面可以展開成平面缺角圓形如下圖(b). 除了 A 點之外任何點的曲率為 0. 因為錐面上一個 close loop, 如果不包含 A, parallel transport 夾角為 0. 因此曲率為 0.
如果包含 A 的圓，parallel transport 夾角 = $\alpha$, 面積 = $(\pi-\alpha/2) a^2$, A 的曲率趨近無窮大。 \(R_A = \lim_{a\to 0}\frac{2\alpha}{a^2(2\pi-\alpha)}\to\infty\)

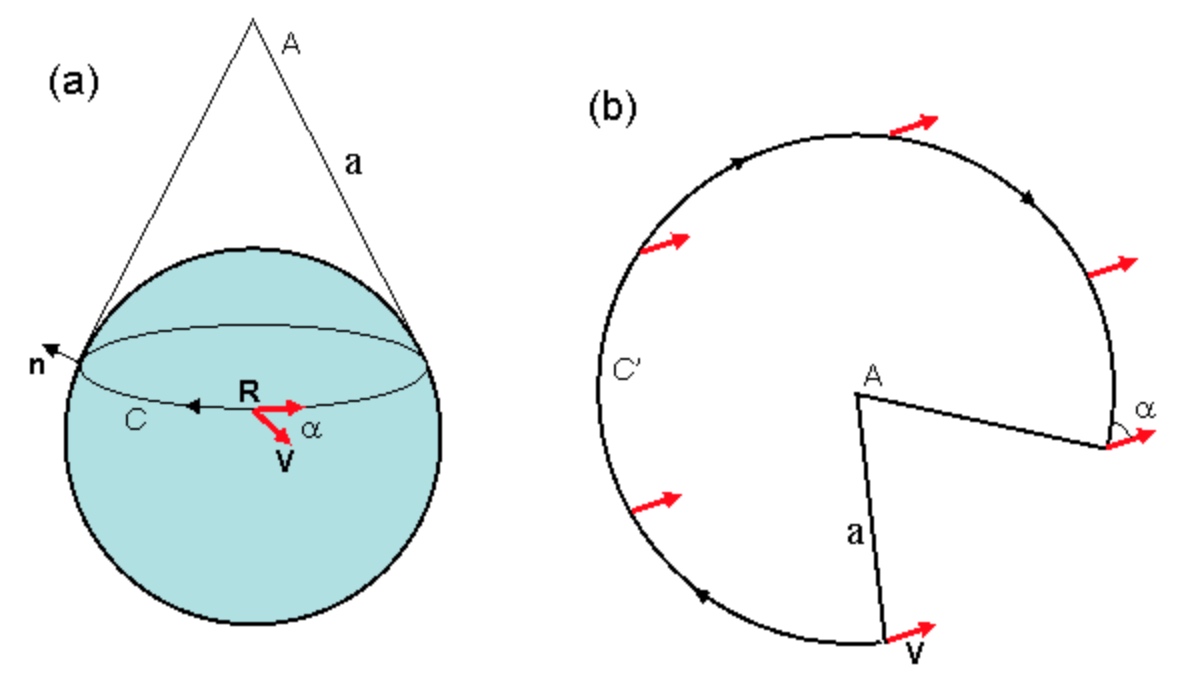
image-15694289220547

另一個問題，上圖球面非大圓 R 的 parallel transport 夾角？ 常見的回答是 0. 錯誤的答案！正確的答案是用圓錐面和球面的切線為 R，再展開如上圖 b.

橢圓幾何：平行移動先定義 geodesic A (上圖左邊弧線), 赤道的 geodesic B 垂直於 A at T. 由平行定理我們知道球面幾何不存在和 A 平行（不相交）的 geodesic. 我們只能選擇和 B 垂直的 geodesic C, given we know A 和 C 會相交於 Q 點（其實在北極）。 此時從 $A_T$ 的切線，一路到 $A_Q$ 都是 parallel transport. 另一路是$A_T$ 經由 $B \to C \to A_Q$ 的 C 的切線（也是 parallel transport) 一定有一個夾角 $\alpha$. 球面幾何的三個內角和 $=90+90+\alpha>180$. 這個夾角和 parallel transport 所包含的面積有關。 如果只是在局部做一個封閉迴路（holonomy），局部看起來就像歐氏空間。Parallel transport 的 holonomy 夾角為 0. Use Gauss curvature $R = angle / area \quad \text{where}\quad area = 4\pi r^2 /2 * \alpha /{2 \pi} = {\alpha r^2}$ \(R= \frac{1}{r^2} \quad \text{independent of }\alpha\)

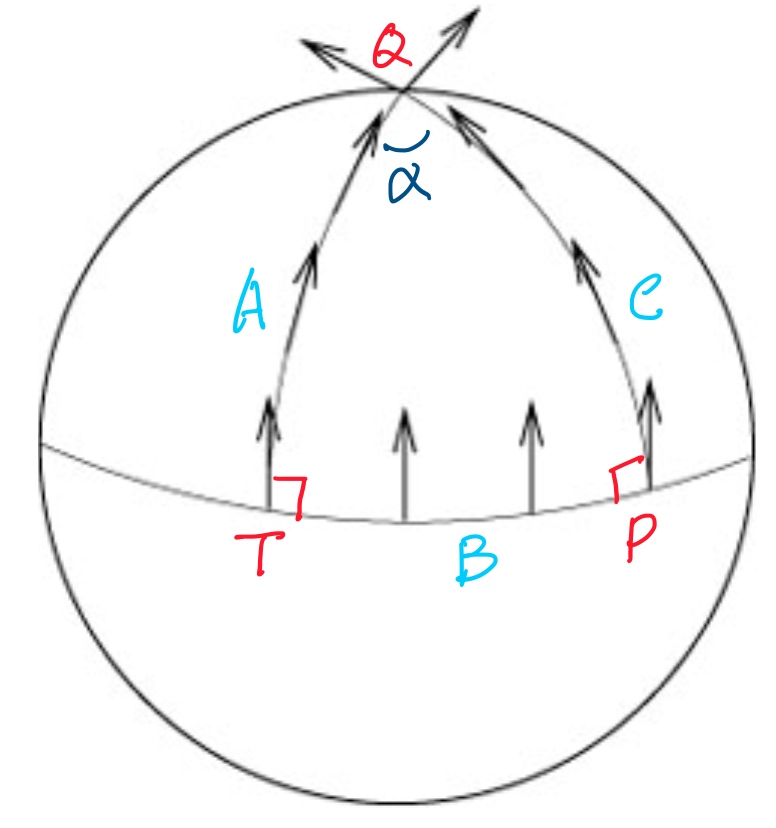
image-15694203363556

雙曲幾何：直接考慮鞍面的三角形，內角和小於 180. parallel transport 的 holonomy 為負夾角。

###

曲率基於 Parallel Transport (平行移動) 的微分定義

(Wiki 2019a) 微分幾何對平行移動的定義： 平行移動是將流形上的幾何特性沿著光滑曲線移動的一種方法。如果流形上有一個 affine connection（covariant derivative)，那麼 affine connection 保證我們可以將流形上的向量沿著曲線移動使得它們關於這個 connection 保持「平行」。

在某種意義上說，關於 connection 的平行移動提供了將流形的局部幾何沿著曲線移動的方法：即「連接」了鄰近點的幾何。有許多種平行移動的概念，但其中一種方式等同於提供了一個 connection。事實上，通常的 connection 是平行移動的無窮小類比。反之，平行移動是 connection 的局部實現。

因為平行移動給出了 connection 的一種局部實現，它也提供了曲率的一種局部實現（holonomy）。Ambrose-Singer 定理明確了曲率與 holonomy 的關係。 \(\frac{D}{dx}\frac{D}{dy}V - \frac{D}{dy}\frac{D}{dx}V = R(\frac{\partial \sigma}{\partial x},\frac{\partial \sigma}{\partial y})V \quad\text{where R is curvature tensor}\)

簡言之，平行移動基本是一種 local connection, 以及實現 curvature 的方式。

如果使用 Christoffel symbol 和其微分，可以推導出以下的結果。

\[\begin{aligned} {\left[\nabla_\gamma \nabla_\beta-\nabla_\beta \nabla_\gamma\right] V_\alpha=\left(\frac{\partial \Gamma_{\alpha \gamma}^\sigma}{\partial x^\beta}-\frac{\partial \Gamma_{\alpha \beta}^\sigma}{\partial x^\gamma}+\Gamma_{\alpha \gamma}^\tau \Gamma_{\tau \beta}^\sigma-\Gamma_{\alpha \beta}^\tau \Gamma_{\tau \gamma}^\sigma\right) V_\sigma} \end{aligned}\]

刮號部分就是 Riemann Curvature Tensor

\[\begin{aligned} R_{\alpha \beta \gamma}^\sigma \equiv \frac{\partial \Gamma_{\alpha \gamma}^\sigma}{\partial x^\beta}-\frac{\partial \Gamma_{\alpha \beta}^\sigma}{\partial x^\gamma}+\Gamma_{\alpha \gamma}^\tau \Gamma_{\tau \beta}^\sigma-\Gamma_{\alpha \beta}^\tau \Gamma_{\tau \gamma}^\sigma \\ \end{aligned}\]

問題是：平行移動和平行公理有什麼關係？

平行公理和平行移動的等價邏輯

局部和全域平行的關鍵聯結 (!PT)

微分幾何連結局部和全域的關鍵：(PT!) Independence of Parallel Transport: If two lines are parallel transports (PT) along one path (or transversal) then they are PT along ALL paths (transversals).

假如可以證明 PT! 和平面幾何等價，就可以把局部 (PT) 性質和全域性質連結在一起！

如何證明 PT! 和平面幾何等價？我們知道平面幾何和三角形内角和 = 180 度 (A=180) 等價。auo

(1) PT! iff A = 180

(2) HSP implies PT!

(3) EFP iff HSP

(4) A = 180 implies EFP

(5) PT! iff H = 0

Form (1)-(4) HSP iff HSP iff A=180 iff PT!

平行公理和 Parallel Transport 和 geodesic 三角形內角和

平行公理：一條直線和線外一點平行直線的關係。 什麼是直線？最直觀的定義就是最短路徑，在非平面的“直線”看起來並不直。 數學的表示是： $ \min \int ds$. 使用變分法的 Euler-Lagrange equation 可以得到 Geodesics (測地線或地直線)。平面幾何的 geodesic 就是直線，推廣到微分幾何如下：

  • 一條 Geodesics (地直線）上所有點的切向量（以及和切線固定夾角的向量）都互相平行（如下圖三條地直線，都是球面上的大圓）。
  • Geodesic (地直線）線外一點和其最短距離的路徑也是 geodesic, 並且垂直夾角。
  • 其實是否直角不重要。如果不是直角但仍是 geodesic，parallel transport 就會轉該夾角。沿著同一條 geodesic 的 parallel transport 和 geodesic 的夾角不變。
  • How to prove？ 如果 geodesic 構成的三角形內角和為 180, parallel transport 的夾角為 0. 大於 180, parallel transport 會產生正夾角。小於 180, parallel transport 產生負夾角。

image-15694203363556