Source
張量分析用於幾何
張量(tensor) 最重要的特性就是座標系無關,可用於平面或曲面。張量分為三類:
- Basis vector invariant: 純量 也就是 0 階張量。
- Basis vector contra-variant. 為什麼 contra-variant? 因為 basis vector scale up, 張量分量會 scale down. 一階張量是 vector (n維), 二階張量 (nxn維), 三階張量(nxnxn維),依此類推。e.g. Einstein curvature tensor 是四階張量(4x4x4x4)維。 Ricci curvature tensor 是二階張量 (4x4)維。
- Basis vector co-variant. 也稱為 one-form. 像是 gradient, $\nabla$, basis vector scale up, dual basis vector scale down, 張量分量也會 scale up. 其他特性和一般張量一樣。
其他的張量運算下面展開。
先用歐氏空間的方向導數為例:
在卡氏座標系(笛卡爾直角座標系):${\mathbf{e_1,\,e_2}}$, global constant orthonormal basis vectors. 曲線和切向量: \(\vec{u} = \frac{d\vec{r}}{d\lambda} = u_1\mathbf{e_1} + u_2\mathbf{e_2}\)
注意:千萬不要用 $[u_1, u_2]$ 表示法,只有在卡氏座標系可用。對於非直角或非歐氏空間一定要如上公式帶上 local basis vectors!!
先考慮 gradient operator, $\nabla$. 在卡氏座標系:
\[\nabla = \frac{\partial}{\partial e_1} \mathbf{e_1} + \frac{\partial}{\partial e_2} \mathbf{e_2}\]一個純量場(0階張量)的梯度, $\nabla \phi$, 是一個向量。更準確的說是一個一階張量。 一個一維量場的梯度, $\nabla \vec{V}$, 是一個二階張量。以此類推。
純量場的方向導數,基本上是純量場的梯度 (gradient) 和方向向量的內積。
\[\nabla_{\vec{u}}\phi = \vec{u}\cdot\nabla\phi = (u_1\mathbf{e_1} + u_2\mathbf{e_2}) \cdot \left(\frac{\partial \phi}{\partial e_1}\mathbf{e_1}+\frac{\partial \phi}{\partial e_2}\mathbf{e_2}\right)\\ = u_1 \frac{\partial \phi}{\partial e_1} + u_2 \frac{\partial \phi}{\partial e_2} \quad\text{where}\quad\mathbf{e_i}\cdot \mathbf{e_j}=\delta_{ij} \quad(1)\,\text{!wrong for non-Euclidean!}\]$\nabla_{\vec{u}}\phi = \vec{u}\cdot\nabla\phi = 0$ 代表 $\vec{u}$ 和梯度 $\nabla \phi$ 垂直。因此 $\vec{u}$ 形成 $\phi$ 的等位線。
(1) 只能用於卡氏座標系。接下來幾個重點:1.座標系無關;2.推廣到曲面;3.簡化公式。 現在引入 covariant/contravariant basis and tensor, 和愛因斯坦 summation notation.
Basis vectors ${\mathbf{e_1,\,e_2}}$, 配合 contra-variant 分量。 Dual basis vectors ${\mathbf{e^1,\,e^2}}$, 配合 co-variant 分量。
\[\mathbf{e_i}\cdot\mathbf{e^j}=\mathbf{e^i}\cdot\mathbf{e_j}=\delta_i^j=\delta_j^i \qquad(2)\]注意 $\mathbf{e_i}\cdot \mathbf{e_j}\ne\delta_{ij}$, 有兩個原因。如果 $\mathbf{e_i}$ 放大兩倍,$\mathbf{e_i}\cdot \mathbf{e_i}=4$, 就是座標系無法 scale. 另外非直角座標系,$\mathbf{e_1}\cdot \mathbf{e_2}\ne 0$, 就是座標系無法非直角。正確的結論如下,可以用於非歐非直角座標系。$g_{ij}$ 是二階張量 (metric tensor) 的分量。 \(\mathbf{e_i}\cdot\mathbf{e_j}=g_{ij} \qquad \mathbf{e^i}\cdot\mathbf{e^j}=g^{ij} \qquad(3)\)
對於歐氏空間非直角座標系,(1) 可以修改為: \(\nabla_{\vec{u}}\phi = \vec{u}\cdot\nabla\phi = (u^1\mathbf{e_1} + u^2\mathbf{e_2}) \cdot (\frac{\partial \phi}{\partial e_1}\mathbf{e^1}+\frac{\partial \phi}{\partial e_2}\mathbf{e^2})\\ = u^1 \frac{\partial \phi}{\partial e_1} + u^2 \frac{\partial \phi}{\partial e_2} = \quad\text{where}\quad\mathbf{e^i}\cdot \mathbf{e_j}=\delta^i_j \qquad(4)\)
使用愛因斯坦 notation 重寫 (4) \(\nabla_{\vec{u}}\phi = \vec{u}\cdot\nabla\phi = u^i\mathbf{e_i} \cdot\partial_j \phi \mathbf{e^j} = u^i \partial_i \phi\qquad(5)\)
曲面空間的方向導數:
曲面空間的純量場方向導數和 (5) 完全相同。因為純量場是 basis invariant.
但是曲面空間的向量場是 basis covariant or contravariant, 所以曲面的向量場的方向導數會比歐氏空間複雜的多。
曲面空間向量場 $\vec{V}$ 的方向 $\vec{u}$ 導數
- 似乎可視每個分量為純量場,求每個純量場的方向導數。Wrong! 原因是 basis vector 在非歐空間不是 constant vector, 甚至歐氏空間的極座標也不是 constant vector. 因此 basis vector 的微分會產生新的 component! (Christopher symbol, or connection).
- 向量場的梯度是二階張量,直接求梯度太複雜。比較好的作法是分解方向導數的“方向向量”為 basis vector linear combination, 最後再結合為真正方向導數。
此處利用 Christopher symbol 以及 $\alpha\to i \,,\, k\to\alpha$ \(\frac{\partial \mathbf{e_\alpha}}{\partial e_\beta} = \Gamma^k_{\alpha\beta}\mathbf{e_k}\) 如果是歐氏空間且直角座標系,Christopher symbol $\Gamma^a_{bc}=0$ 如果是歐氏空間但極座標系,因為每一點的 local basis vector 方向都不同,Christopher symbol 不為 0, 一共有 2x2x2=8 個 components [@cyrilChristoffelSymbol2016].
\[\Gamma_{i j}^{r}=\left(\begin{array}{cc}{\Gamma^r_{\theta\theta}=-r} & {0} \\ {0} & {0}\end{array}\right) \qquad \Gamma_{i j}^{\theta}=\left(\begin{array}{cc}{0} & {\frac{1}{r}} \\ {\frac{1}{r}} & {0}\end{array}\right)\]愛因斯坦 notation and convention: 向量場的梯度微分是二階張量(樓上加樓下)。 \(\nabla_{e_\beta}\vec{V}= \nabla_\beta V^\alpha = \partial_\beta V^\alpha+\Gamma^{\alpha}_{i\beta} V^i = \partial_\mu V^\nu+\Gamma^{\nu}_{\lambda\mu} V^\lambda\)
最後 \(\nabla_{\vec{u}}\vec{V} = \vec{u}\cdot\nabla\vec{V} = (u^1 \mathbf{e_1} + u^2 \mathbf{e_2})\cdot\nabla\vec{V}\\ = u^\beta (\frac{\partial V^\alpha}{\partial e_\beta} + V^i \Gamma^{\alpha}_{i\beta})\mathbf{e_\alpha} = (u^i \frac{\partial V^k}{\partial e_i} + u^i V^j \Gamma^{k}_{ij})\mathbf{e_k} = (u^i {\partial_i V^k} + u^i V^j \Gamma^{k}_{ij})\mathbf{e_k}\)
愛因斯坦 notation and convention: 向量場的方向導數是一階張量(樓上)。 \(\nabla_{\vec{u}}\vec{V} = u^i {\partial_i V^k} + u^i V^j \Gamma^{k}_{ij}\)
整理愛因斯坦 notation 的原則:
- $\vec{u}=u^i\mathbf{e_i}=u^i$, 只有一個樓上 index,代表一階張量 contra-variant.
- $\nabla\phi = \partial_i \phi \mathbf{e^i} = \partial_i \phi$, 只有一個樓下 index,代表一階張量 co-variant (one-form).
- $\vec{u}\cdot\nabla\phi = u^i \partial_i \phi$, 張量和 1-form 張量內積結合,同一個 index i 樓上樓下抵銷,變成 0 階張量(純量)。
- 張量微分(gradient) 階數+1:$\nabla$(0 階張量)得到一階 one form 張量;$\nabla$(一階張量)得到二階張量;以此類推。$\nabla_\beta V^\alpha = \partial_\mu V^\nu+\Gamma^{\nu}_{\lambda\mu} V^\lambda$ 是二階(樓上加樓下)tensor.
- 張量和 one-form 張量內積 階數-1,index 樓上樓下抵銷。
- 張量場的方向導數是先微分張量(+1)場再和方向向量內積(-1),階數不變,e.g. 純量場方向導數是純量。向量場的方向導數是一階張量:$\nabla_{\vec{u}}\vec{V} = u^i {\partial_i V^k} + u^i V^j \Gamma^{k}_{ij}$ 是一階(樓上) 張量。
- 因為張量場的方向導數階數不變。因此可以重覆這個運算。最常見是二次方向導數(沿不同的方向,如 basis vectors)。除了在平面歐氏座標系以外,一般是不能交換。$\nabla_{\vec{w}}\nabla_{\vec{u}}\vec{V} \ne \nabla_{\vec{u}}\nabla_{\vec{w}}\vec{V}$. 事實上,$\nabla_{\vec{w}}\nabla_{\vec{u}}\vec{V} - \nabla_{\vec{u}}\nabla_{\vec{w}}\vec{V} = R\vec{V}$? (TBC)
回到曲線的方向導數=絕對導數(Absolute Derivative:等高線,地直線,平行移動)
曲線和切向量回顧:
\(\vec{u} = \frac{d\vec{r}}{d\lambda} = u_1\mathbf{e_1} + u_2\mathbf{e_2}\)
純量場的線方向導數
\(\nabla_{\vec{u}}\phi(\vec{r}) = \frac{d\vec{r}}{d\lambda}\cdot\nabla\phi(\vec{r}) = \frac{d\phi(\vec{r})}{d\lambda}\)
其實這就是著名的 gradient theorem, 或是線積分基本定理推廣到曲面。重點是曲面線積分是路徑無關!或是封閉迴路線積分為 0. 但在向量場不是如此。
\(\int_p^q \nabla_{\vec{u}}\phi(\vec{r}) d\lambda
= \int_p^q \nabla\phi(\vec{r})\cdot d\vec{r} = \phi(q) - \phi(p)\)
以純量場為例
Let $\phi(\vec{r}) = |\vec{r}|^2$ 座標系無關: 射線運動卡氏座標系: $\phi = x^2 + y^2$ and $\nabla \phi = 2x \mathbf{e_x} + 2y \mathbf{e_y} $ $\vec{r} = c_0\lambda\mathbf{e_x} + c_1\lambda\mathbf{e_y}$, where $c_0^2+c_1^2=1$ $\frac{d\vec{r}}{d\lambda} = c_0\mathbf{e_x} + c_1\mathbf{e_y}$
\[\nabla_{\vec{u}}\phi(\vec{r}) = \frac{d\vec{r}}{d\lambda}\cdot\nabla\phi(\vec{r}) = 2x c_0 + 2y c_1= 2\lambda c_0^2 + 2\lambda c_1^2 = 2\lambda\]$\phi(\vec{r}) = \phi(\lambda) = c_0^2 \lambda^2 + c_1^2 \lambda^2 = \lambda^2$ \(\frac{d\phi(\vec{r})}{d\lambda} = 2\lambda\)
射線運動極座標系: $\phi = r^2$ and $\nabla \phi = 2r \mathbf{e_r}$ $\vec{r}= \lambda \mathbf{e^r} + \theta_o \mathbf{e^\theta}$ $\frac{d\vec{r}}{d\lambda} = \mathbf{e_r}$
\[\nabla_{\vec{u}}\phi(\vec{r}) = \frac{d\vec{r}}{d\lambda}\cdot\nabla\phi(\vec{r}) = 2r = 2\lambda\]$\phi(\vec{r}) = \phi(\lambda) = \lambda^2$ \(\frac{d\phi(\vec{r})}{d\lambda} = 2\lambda\)
以向量場為例
向量場的線方向導數,稱為絕對導數(absolute derivative) \(\nabla_{\vec{u}}\vec{V}(\vec{r}) = \frac{d\vec{r}}{d\lambda}\cdot\nabla\vec{V}(\vec{r}) \\ = u^i {\partial_i V^k} + u^i V^j \Gamma^{k}_{ij} = \frac{d V^k}{d\lambda} + \frac{d x^i}{d\lambda} V^j \Gamma^{k}_{ij}\)
Parallel transport
$\vec{u} = \frac{d\vec{r}}{d\lambda}$ or $u^k = \frac{dx^k}{d\lambda}$, parallel transport 就是向量場 $\vec{V}$ 沿 $\vec{r}$ 方向導數為 $\vec{0}$,上式變成: \(\frac{d V^k}{d\lambda} + \frac{dx^i}{d\lambda} V^j \Gamma^{k}_{ij}=0\)
積分形式: $V^k(q) - V^k(p) = -\int_p^q V^j\Gamma^{k}_{ij}{dx^i}$. 注意 p 點和 q 點的 basis vectors 不一定相同。即使 $V^k(p) \ne V^k(q)$ 也不代表 $\vec{V}(p) \ne \vec{V}(q)$. 下面極坐標例子可以看出。 另一個重點是 $V^k(q)$ 有很多 $dx^i$ 可以到達,結果不一定相等!(path dependent)
卡氏座標系:$\Gamma=0$, $V^k = c^k$, constant as expected.
極座標系:$k ={r \,, \theta }$; $ds^2 = dr^2 + r^2 d\theta^2$.
$|\mathbf{e^r}| = \frac{\partial s}{\partial r} =1$
$|\mathbf{e^\theta}| = \frac{\partial s}{\partial \theta} =r$
$\vec{x} = x^r \mathbf{e^r} + x^\theta \mathbf{e^{\theta}}$ \(\frac{d V^r}{d\lambda} + \frac{dx^i}{d\lambda} V^j \Gamma^{r}_{ij} = \frac{d V^r}{d\lambda}-\frac{dx^\theta}{d\lambda}V^\theta x^r= 0\)
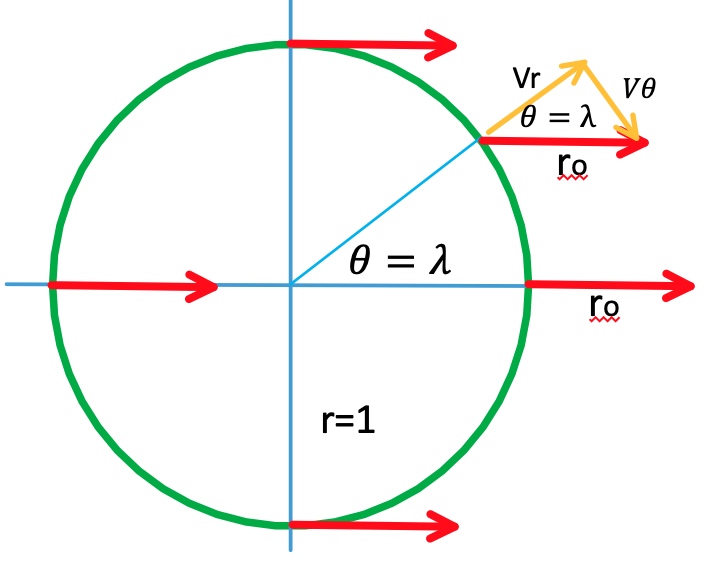
\[\frac{d V^\theta}{d\lambda} + \frac{dx^i}{d\lambda} V^j \Gamma^{\theta}_{ij} = \frac{d V^\theta}{d\lambda} + \frac{dx^r}{d\lambda} \frac{V^\theta}{x^r} + \frac{dx^\theta}{d\lambda} \frac{V^r}{x^r} = 0\]Example 1: 射線運動 (起點在r=1上) Let $x^r = \lambda+1\,,\, x^\theta = c$. $\vec{V}(\lambda=0) = r_o \mathbf{e^r} + \theta_o \mathbf{e^\theta}$ \(\frac{d V^r}{d\lambda} = 0\)
\[\frac{d V^\theta}{d\lambda} + \frac{V^\theta}{\lambda+1} = 0\]$V^r = r_o \,,\, V^\theta = \frac{\theta_0}{\lambda+1} = \frac{\theta_0}{x^r} \text{ Yes, scale down the basis vector } e^\theta $
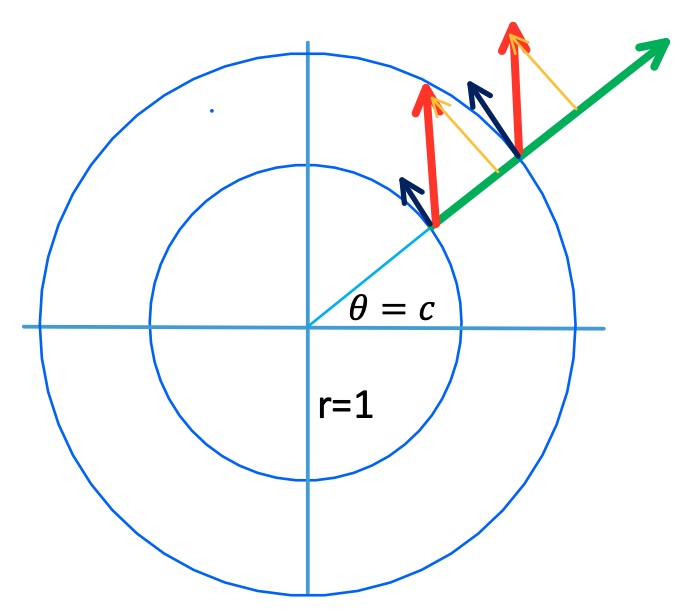
Example 2: 圓周運動 Let $x^r = 1\,,\, x^\theta = \lambda$. 弧長等於夾角! $\vec{V}(\lambda=0) = r_o \mathbf{e^r}$ \(\frac{d V^r}{d\lambda}-V^\theta = 0\)
\[\frac{d V^\theta}{d\lambda} + V^r = 0\]$V^r = r_o\cos\lambda \,,\, V^\theta = -r_o\sin\lambda$ as expected below.