曲率 Curvature

Posted on | In

Source

Eigenchris: very good YouTuber on Tensor and differential geometry: https://www.youtube.com/watch?v=optrC-0HhMI&ab_channel=eigenchris

http://wordpress.discretization.de/geometryprocessingandapplicationsws19/connections-and-parallel-transport/. Connection and Parallel Transport

Math 302 Parallel Postulates

file:///Users/allenlu/Downloads/9781429799850-14.pdf link parallel transport with parallel postulate

Introduction

人類是視覺的動物，我們是如此習慣 global view 對於一些 global view take for granted.

例如：直線，平行，… 都是一眼可以看出來，但是定義起來要花一些思考。如何轉換的曲面就要小心。

直線：兩點間最短的路徑 -> 可以直接推廣到曲面。

平行：兩條直線永遠不相交。或是兩條直線之間等距離。這兩者在平面等價，但在曲面不是。例如北緯 10 度線和赤道是等距離也不相交。但是北緯 10 度線不是曲面的直線（大圓）！但是赤道是曲面的直線（大圓）。

就像我們如此習慣 10 進位因為有 10 隻手指頭。對於轉換到 2 進位，8 進位，16 進位需要大腦的 extra-time to process.

所以直線，平行線還有用嗎？ Yes!! 非常有用，但是 go local, 就是 parallel transport.

幾何根據全域或局部以及外視或内視可以略分為 4 類：

  • Local (局部): 基於非常小區域 (微分=無窮小) 的特性，例如曲率 (curvature)、connection (covariant derivative)

  • Global (全域): 基於 loop、transversal (軌跡)、大區域的特性，例如圓周率、三角形内角和、曲面的形狀
  • Extrinsic view (外視): birds-eye-view (上帝視角) 即是 manifold 是嵌入更高維的歐式空間 (X, Y, Z 卡氏座標)
  • Intrinsic view (內視): bugs-eye-view (毛毛蟲視角) 沒有參照坐標系，只能靠 manifold 本身的 objects (綫，角度，平行移動) 推導 manifold 的性質。結果應該和 extrinsic view 結果一致。

一個的例子説明不同的方式定義“曲率”。

直綫 Extrinsic (Birds-Eye-View) Intrinsic (Bugs-Eye-View)
Global (大區域) 近似橢圓球對應的半徑 Holonomy (H), 三角形内角和 (A), 圓周率
Local (非常小區域，微分) 近似局部橢圓球對應的半徑 (K1, K2, K1K2, or K1+K2/2) 平行移動的二次微分

如何定義曲率 (Curvature)？

(Global -> local) 極限定義

  1. 三角形内角和
  2. 圓周或圓面積

    image-20230716201141245

    • C 是圓周，A 是圓面積，$r$ 是manifold 上圓的半徑 (内視)。如下圖
    • 平面：$\rho_G = 0$
    • 球面：$\rho_G > 0$
    • 雙曲面：$\rho_G < 0$

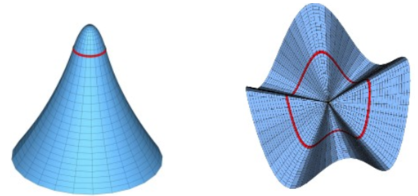
    image-20230716195002692

很直觀，但是數學上不好用。同時 miss 很多 curvature tensor information.

(Local) 微分定義

(外視) Gaussian Curvature (2D, 二維 manifold)

line curvature $K_1, K_2$, 對應 max and min line curvature.

$K = K_1 K_2$: Gaussian curvature; $\frac{K_1 + K_2}{2}$: Mean curvature

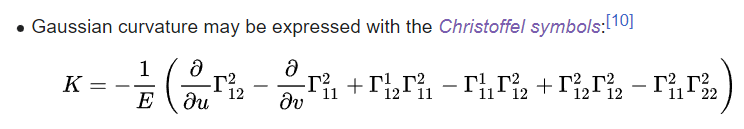
image-20230716201354894

Parallel transport -> holonomy -> 平行四邊形的 parallel transport difference, 也就是二次微分 -> (Riemann) curvature

(内視) 黎曼曲率張量 (Riemann Curvature Tensor)

image-20230716140604149

上式 1 是坐標不變 (invariant) 的曲率張量定義。

  • 黎曼曲率 $R(\vec{u},\vec{v})$ 是二次微分，作用在 vector。

  • 最後一項是和 torsion term (旋轉)。一般我們都會假設是 torsion-free 幾何，所以此項為 0.1

上式 2 是分量的表示方式，和選擇的坐標系相關 (逆變 contra-variant，協變 covariant)

  • 黎曼曲率張量是二次微分，對應 2 covariant. 不過一般的標準寫法是 $R^d_{cab}$ 是 (1 contra-variant, 3 covariant)。why?

  • 黎曼 4 階 (1 contra-variant, 3 covariant) 張量的分量數量

    • 2D plane: 2x2x2x2 = 16 elements

    • 3D space: 3x3x3x3 = 81 elements

    • 4D space-time: 4x4x4x4 = 256 elements

黎曼曲率張量看起來有很多分量，不過這個曲率張量其實有很多對稱性。並非所有分量都需要計算。

  • 12,34; bianity identity, …

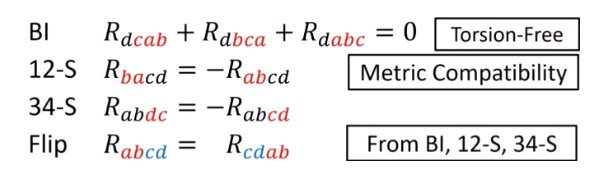
image-20230716021338220

Parallel transport -> geodesic -> geodesic deviation -> (Ricci tensor) curvature

Ricci Curvature Tensor 的數學定義

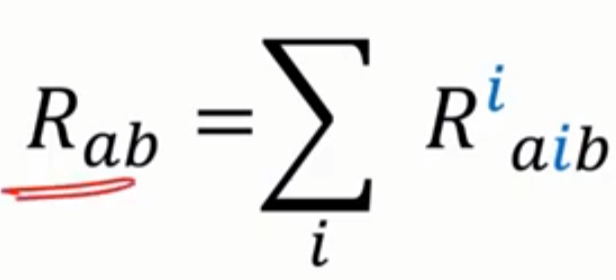image-20230716153427260 = $R_{ab}$

  • 爲什麽不用第一和第三個 Riemann tensor contraction? 因爲第一個 = 0, 第三個和 Ricci tensor 一樣！

Ricci curvature tensor 是 2 階 tensor

  • 2D plane: 2x2 = 4 elements
  • 3D space: 3x3 = 9 elements
  • 4D space-time: 4x4 = 16 elements (愛因斯坦的廣義相對論使用 Ricci curvature tensor)

Ricci tensor 是對稱: $R_{ab} = R_{ba}$

Ricci (Curvature) Scalar

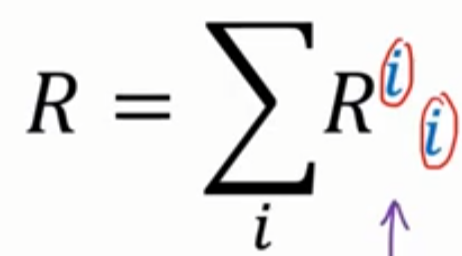image-20230716153631842= R (Scalar)

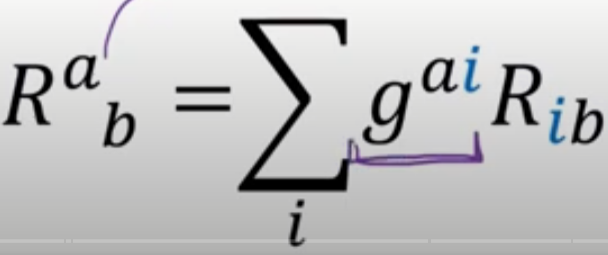image-20230716153659849= $g^a R_b$

Ricci Curvature Tensor (rank-2) and Scalar (rank-0) 物理意義

Geodesic deviation vector: S (separation vector)

  • (平面) R = 0, S 的二次微分 = 0, 也就是 S 是 affine (connection). 例如平面的 geodesics 是直綫, S 散開的速度是綫性。
  • (球面) R > 0, S 的二次微分 < 0, 也就是 geodesics 從赤道出發，會趨向一起在北極，而且不是綫性趨近。
  • (球面) R > 0, S 的二次微分 > 0, 也就是 geodesics 從鞍面出發，會非綫性發散。

此處 R 是 Riemann curvature

image-20230715182630093

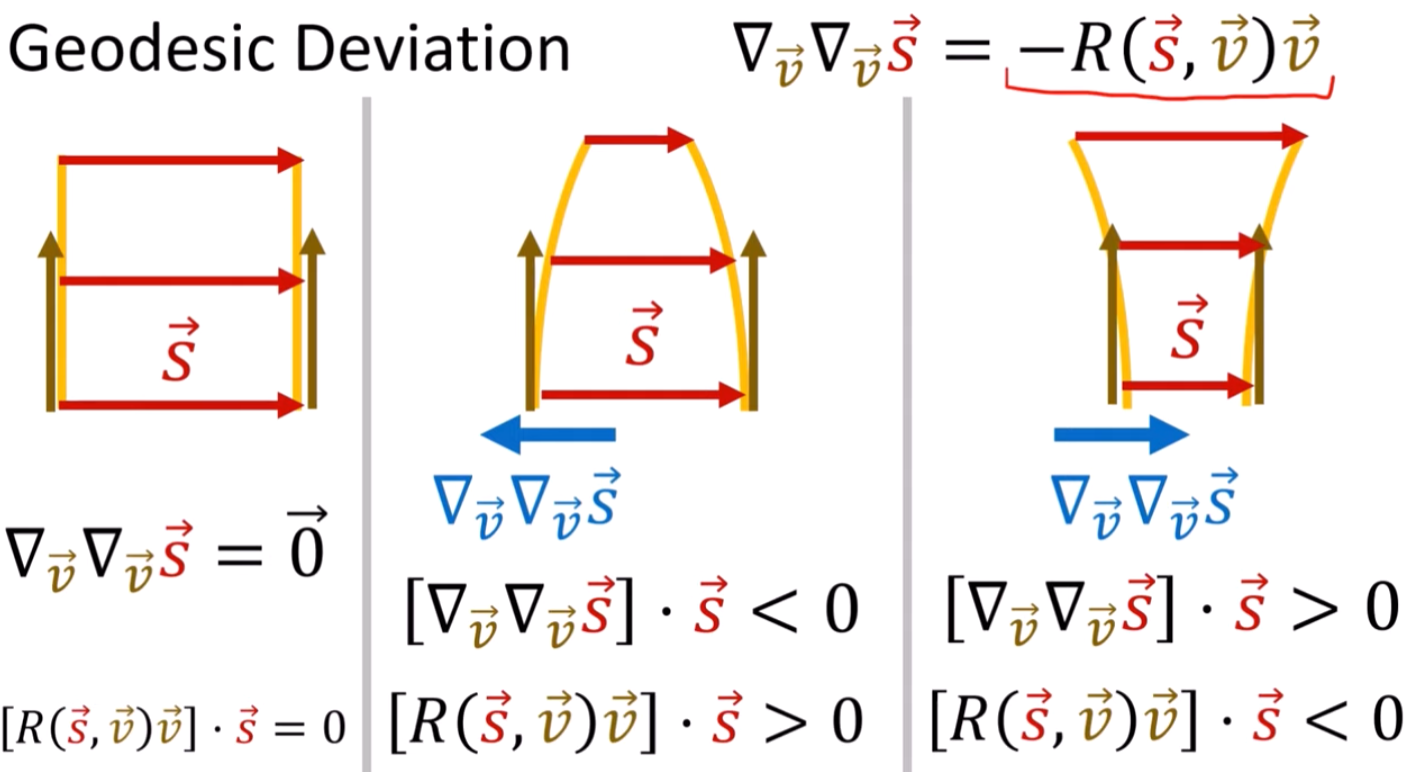
image-20230715184532658

定義 Section Curvature = Normalized geodesic deviation 二次導數和 geodesic deviation 的内積！

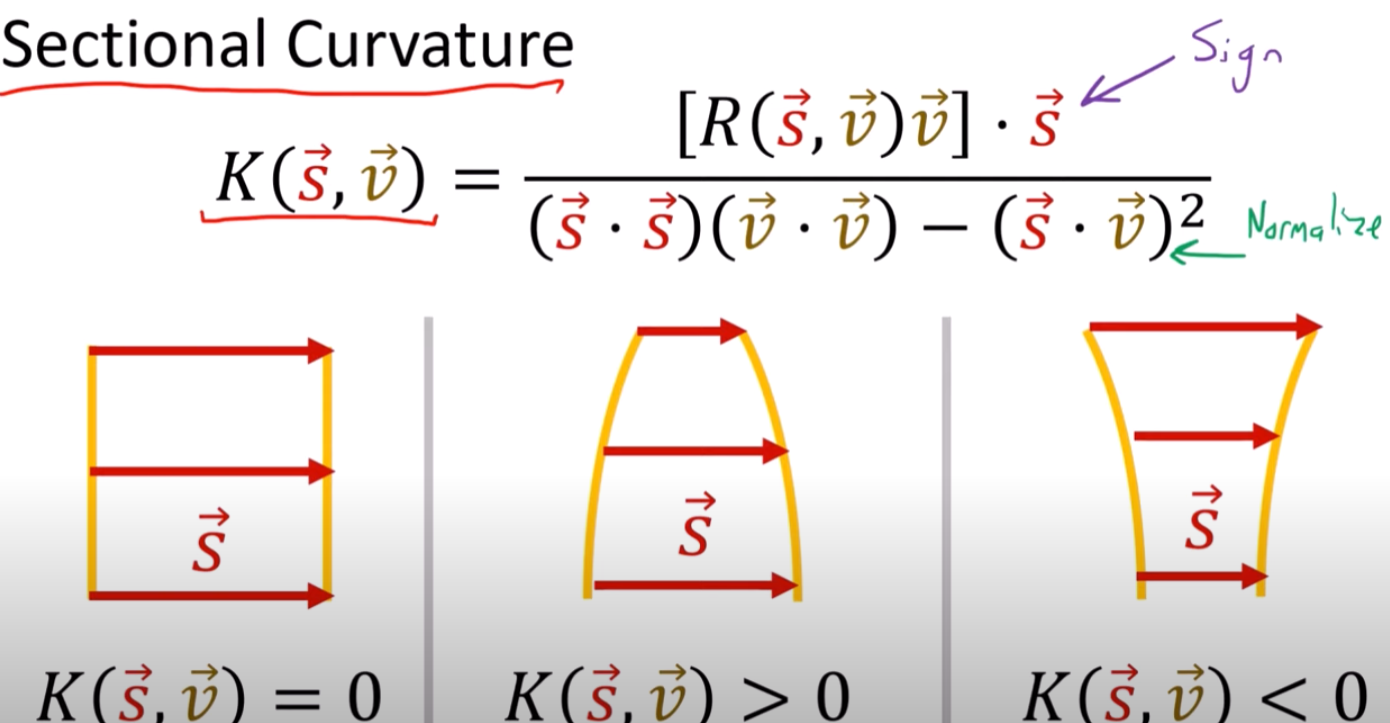
image-20230715192139653

Ricci Curvature Tensor (from Riemann Curvature Tensor)

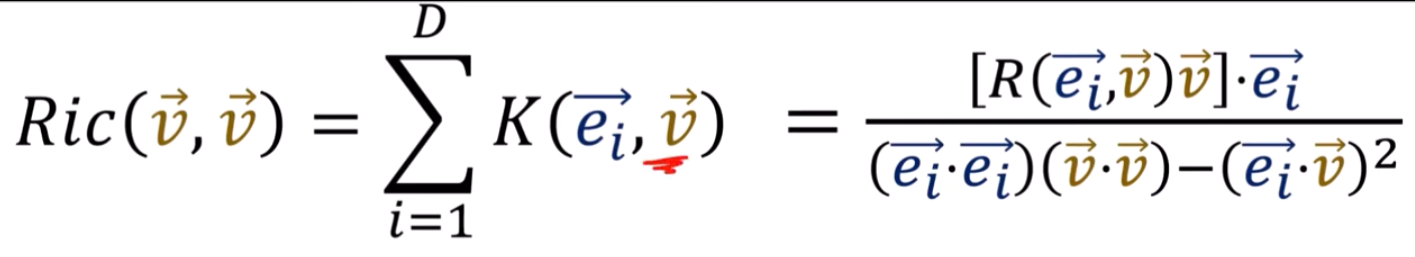
image-20230715192953027

image-20230715193047904

image-20230715192930125

實例

Gaussian curvature (只有在 2D manifold)

One particularly close connection occurs for a 2-dimensional surface S� in 3-dimensional space. The Ricci curvature at a point P∈S�∈� is equal to the Gaussian curvature (because in 2 dimensions there’s nothing to contract in the contraction formula that you give). And the Gaussian curvature is equal to the product of two different geodesic curvatures, namely the so-called “principle curvatures” which are the maximum and minimum values of τ� for curves passing through P�.

Ricci scalar 在 2D manifold 基本等同於 Gaussian Curvature.

image-20230716203120659

Ricci tensor 作用在 2D basis 所得到的就是 Gaussian curvature.

How about Gaussian vs. Riemann?

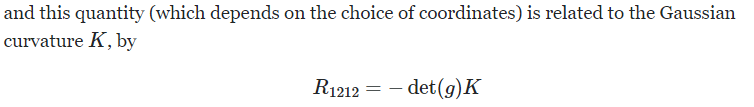
image-20230716203305623

Riemann

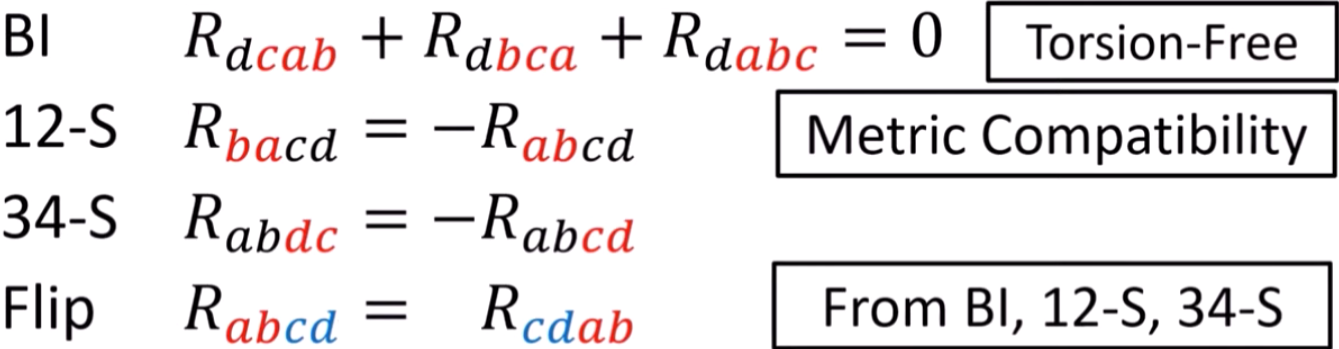
image-20230715085652263

2x2x2x2 = 16 in 2D

image-20230715085838236

polar and 2-S

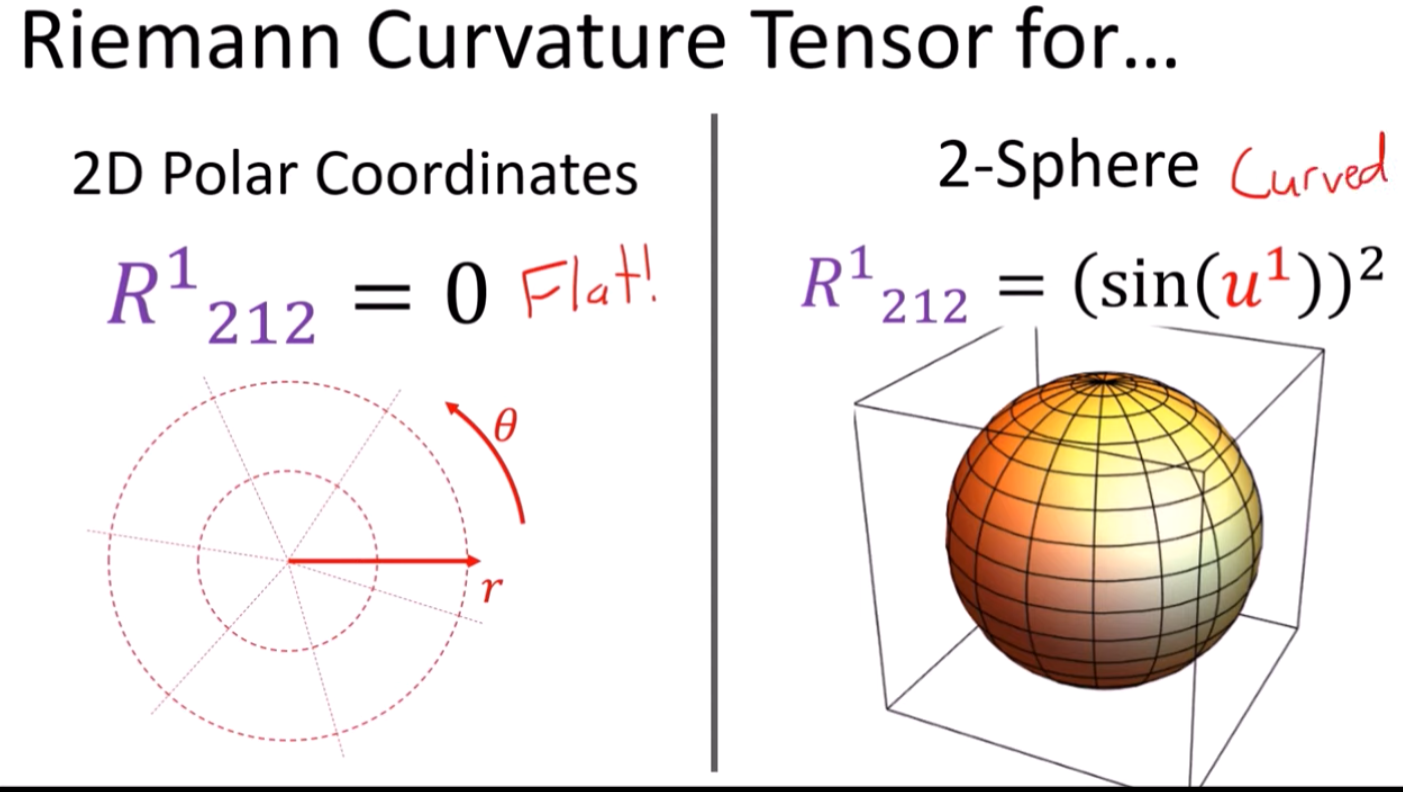
image-20230715090140558

4D : 4x4x4x4 = 256

Ricci Tensor and Scalar

image-20230715091144839

Example Ricci

2 plane

image-20230715193246788

廣義相對論 (10 unique equations)

image-20230716154453907

image-20230716154633806

  1. Dirac 結合量子力學和相對論是否可以從 torsion term 開始? Lie bracket. ↩