無限旅館悖論

Posted on | In

$\infty$ 無窮酒店悖論：探討可數與不可數

「無窮酒店悖論」是一種奇妙的方式，用來說明數學中「可數」和「不可數」的概念區別。讓我們深入探討無窮酒店，以及它如何與這些概念相關聯。

無窮酒店悖論

想像一下，你有一家擁有無窮多間房間的酒店，每間房間都標有正整數（1、2、3、⋯）。儘管擁有無窮多間房間，這家酒店完全住滿了，每個房間都有一位賓客。

現在，一位新賓客來到酒店，你可能會想，我們如何容納這位新賓客，而不用驅逐任何現有賓客呢？答案在於無窮的性質。

可數無窮

在無窮酒店悖論的背景下，自然數的集合（1、2、3、⋯）代表了可數無窮。之所以稱之為可數，是因為你可以在自然數和酒店房間之間建立一對一的對應。

當一位新賓客到來時，你可以將現有賓客移至下一號房間（房間1的所有人移至房間2，房間2的所有人移至房間3，以此類推）。這個過程可以無窮無盡地進行，容納無窮多位新賓客，儘管酒店最初已滿。數學語言：

  • 原來住 $N$ 號房間的賓客移至 $N+1$號。一位新賓客住 1 號房。

在可數無窮集合中，每個元素都可以被指定一個唯一的自然數，這使得建立一對一映射成為可能。

當可數的無窮多新賓客 （1、2、3、…）到來時。我們可以依樣畫葫蘆。

  • 原來住 $N$ 號房間的賓客移至 $2N$號。新賓客 $k$ 住 $2k-1$ 號房。

以上的無窮多是一個旅行團。假設有可數無窮多旅行團，並且每一團都有可數無窮多的新賓客。你要如何安排？

這其實是把 1 維的可數無窮多推廣到 2 維的無窮多：可數無窮多賓客對應 $x$ 軸，可數無窮多旅行團對應 $y$ 軸。

答案是仍然可以做到。可以參考 Youtube video:

The Infinite Hotel Paradox will blow your mind - Alltop Viral

这是一个数学无法回答的问题 #高等数学 #math (youtube.com)

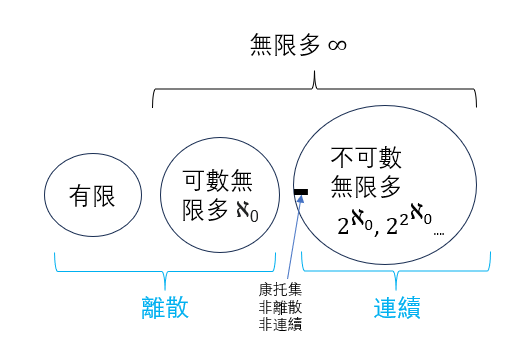
簡言之，可數無窮多是好的無窮多 $\infty$​，當然也有不好的無窮多。就像膽固醇有好的膽固醇 (HDL)，也有壞的膽固醇 (LDL)。

  • 可數無窮多的記號 Aleph-zero：$\aleph_0$, 包含有整數，有理數。​

  • 不可數的無窮多包含：$2^{\aleph_0}, 2^{2^{\aleph_0}}, ….$ 有可數無窮多個。
  • 著名的連續統假設 (Continuum Hypothesis, CH 問題) 就是不存在介於 $\aleph_0$ 和 $2^{\aleph_0}$ 的無窮多 $\aleph_1$，也就是 $\aleph_1 = 2^{\aleph_0}$​
  • 所以如果要裝，就不要用 $\infty$，而是用 $\aleph_0$ 或 $2^{\aleph_0}$ 分別代表可數無窮多和 （1 階級）的不可數無窮多。

不可數無窮

另一方面，0到1之間的實數集合 （稱爲連續統 continuum）是不可數無窮的一個例子。無法與自然數建立一對一的對應，因為在0到1之間的實數比自然數多。

這個觀點是，儘管自然數集合和實數集合都是無窮的，但它們在大小上存在差異。實數集合是一種更大的、不可數無窮。

結論

  • 無窮酒店悖論突顯了數學中無窮集合的迷人且有時反直覺的性質。可數無窮允許與自然數的一對一映射，而不可數無窮涉及到更大的集合，無法使用自然數進行詳盡列舉。
  • 可數無窮多的例子：所有的自然數；所有的整數；[0, 1] 所有的有理數；所有的有理數；所有的 “整複數 a + bi, a, b 都是整數”。所有的可數無窮多都是一樣大，因爲都可以和自然數集合一一對應 ${N: 1, 2, 3,… }$，稱爲 $\aleph_0$
  • 不可數無窮多的例子：[0, 1] 所有的無理數、實數；所有的無理數、實數。不可數的無窮多並沒有等價的關係。
  • 一一對應非常重要，可以用來證明不可數無窮多之間的等價。例如有限長的綫段和無限長的綫段都是 $2^{\aleph_0}$ 因爲可以一一對應。
    • 因此，綫段的長度並不是判斷不可數無窮多的標準！
    • 所有可數無窮多的點集都是 measure-0 (零測度)，因爲可以用 {$\epsilon, \frac{\epsilon}{2}, \frac{\epsilon}{4}, …$} 的區間覆蓋，並讓 $\epsilon \to 0$
    • 不可數的無窮多可以是 measure-0! (e.g. Cantor set)，也可以是 1 (例如實數 [0, 1])，也可以是無窮長 [0, $\infty$].
  • 還有一個重要的點，建構不可數無窮多可以從可數無窮多的子集，但不是用有限多元素的子集趨近無現大。而是一開始的 base 就是 $\aleph_0$，參考 YouTube video, 無窮旅館開燈的問題 (state -> 子集)。
    • $2^{\aleph_0} \ne \lim_{n\to\infty} 2^{n}$

如果以上的可數無窮多和不可數的無窮多讓你覺得驚訝。或是覺得數學家太無聊，硬要把無窮多分成不同的無窮多。

接下來的測度可能驚到下巴掉下來。不過我們將發現一切都是有意義和目的，最終可數無窮大和測度成爲實數分析或是更接地氣的微積分堅實基礎。

測度 (Measure)

Takeaway

  • 外容量 = 稠密性位置的長度和。稠密性即是位置附近有無限多元素。
  • Lebesgue measure = 超級稠密性位置的長度和。超級稠密性即是位置附近有不可數的無限多元素。

集合

我們在上數學課或是編程都熟悉集合 (set)，基本是一群有限或無窮多的元素。在 python 編程中有集合 (set) 和字典 (dict)。 set 就是我們現在討論的集合。Dict 也可以視爲一種集合，但每個元素還成對的，包含 key 和 value, key -> value. 這其實是函數 $f(x) \to y$ 的概念：$x$ 就是 key，$y$​ 就是 value.

（數學）集合還能分成可數集跟不可數集，意思就是這個集合中的元素能不能用數的，可數集又可以分成有限集與無限集（對你沒看錯，無限集也可以是可數的）。例如，有理數集合為可數集和無限集，無理數集合為不可數集。這部分就是酒店悖論的故事。

  • 所有的有限集都是可數的，對應自然數 {1, 2, …, K}。
  • **所有可數無限集基本是等價 (一一對應) = $\aleph_0$ **！
    • 性質可以先用可數有限集接近，然後讓 $n\to\infty$ 得到。但仍然不同：$\aleph_0 + k = \aleph_0$, $\aleph_0 + \aleph_0 = \aleph_0$, ${\aleph_0}^k = \aleph_0$, $k$ 是任意整數。
    • 所有離散的集合都是可數集合：有限集，可數無限集，可數無限個可數無限集？
      • 可數無限多個可數無限多 (${\aleph_0} \times {\aleph_0} = {\aleph_0}$) 是可數無限多
    • 可數無窮多點集都是 measure-0.
  • 不可數的無限集的性質則可能非常不同。
    • 不可數無窮多比可數無窮多多。最簡單就是無窮旅館，每個房間可以開燈或關燈，對應實數。但無法和房間一一對應：$\aleph_0 < 2^{\aleph_0}$
    • 存在無窮多個不可數無窮多集合，而且：$2^{\aleph_0} < 2^{2^{\aleph_0}} < …$
    • $2^{\aleph_0}$​ 的點集可以是 measure-0, 1, 或是無窮長！​
    • 可數無窮多房間，每一個房間 states 有可數無窮多， 所有子集是 ${\aleph_0}^{\aleph_0} = 2^{\aleph_0}$ .
      • 證明：$2^{\aleph_0} \le {\aleph_0}^{\aleph_0} \le ({2^{\aleph_0}})^{\aleph_0} = 2^{\aleph_0 \cdot \aleph_0} = 2^{\aleph_0}$

連續集合和離散集合

如果一個集合由孤立點組成，意味著集合中的任意兩點之間有最小距離，那麼這個集合被認為是離散的。

如果一個集合包含給定區間內的所有點，意味著沒有間隙，那麼這個集合被認為是連續的。

既然説到離散集合，此處好像少了一個重要的集合：連續性集合。例如開集合 ${(0,1)}$，閉集合 ${[0,1]}$。注意這裏的連續性是指在定義域，不是在微積分裏值域的連續性。這正是本文後面要探討的。先列一些我的臆測

  • 連續的集合一定有無限多元素。
  • 連續的集合可以是不可數無限多，例如一段實數。但可能是可數無限多嗎，No. 因爲一定有間隙。
  • 著名的連續統假設已經確定 $\aleph_0 < \aleph_1$, 而是要確定是否 $\aleph_1 = 2^{\aleph_0}$. 也就是連續一定是不可數無限多！

image-20240707223152672

編程計算

  • 編程的元素基本是離散（有限或是可數的無限多）元素。

  • 以下和編程計算僅僅類比，沒有實質的意義：

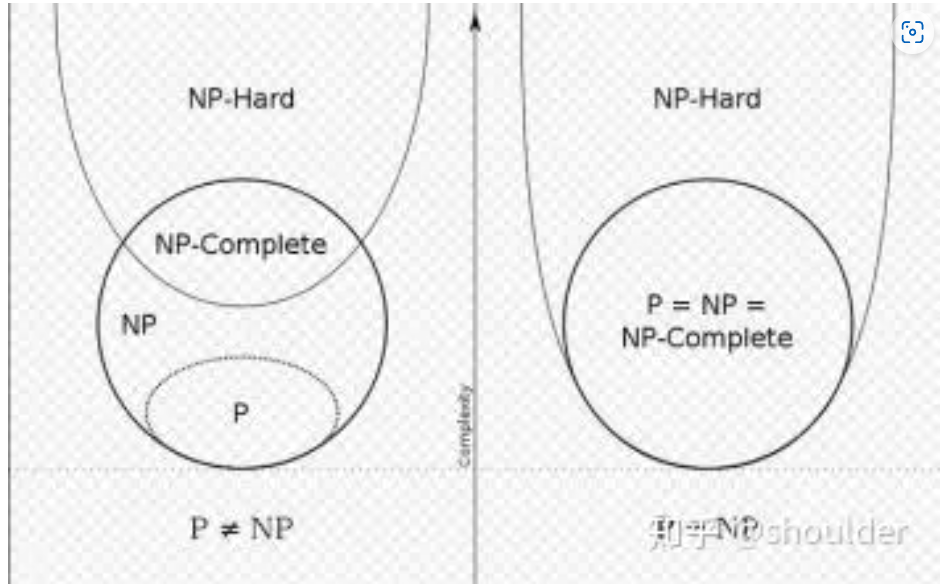
    • P (Polynomial) 問題 : 有限或是可數無限多

    • NP (Non-deterministic Polynomial) 問題：可數無限多

    • NPC (Non-deterministic Polynomial Complete) 問題：可數無限多

    • NP hard 問題：不可數無限多

      image-20240209100550628

測度 (Measure)

如何測量一個集合？這裏的測量不是算有多少元素。因爲存在不可數的集合！

而是回歸長度或面積的概念，使用 （開）綫段包含的方式建立集合的上界和下界。 從而測度 (measure) 一個集合。

我們看一個例子: $S = {1, \frac{1}{2}, \frac{1}{3},…}$​

注意 0 一定是一個下界，因爲長度或面積一定大於等於 0. 所有 measure 或是 metric 都如此。

上界一: 外容量 (Outer content，the same as outer measure?) : 有限區間長度和，最寬區間極限趨 0

更直觀的理解：外容量 = 稠密性位置的長度和

19 世紀的數學家 Harnack 提出一個外容量的觀念，就是一個上界。包含

  • 有界集
  • 有限個開區間的長度和

對於 $S$ 集合，我們可以考慮如下的外容量（3 個區間）：

image-20240208234632337

顯然我們可以藉助增加區間改進外容量（5 個區間），如下圖。

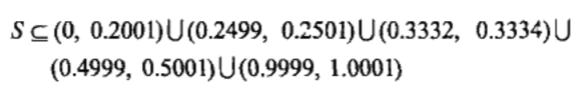
image-20240208235022490

最左邊的區間 (0, 0.2001) 覆蓋除了 1/4, 1/3, 1/2, 和 1 以外的所有點。而這 4 個點都用各自的小區間包覆。此時的長度是 0.2001+0.0002+0.0002+0.0002+0.0002=0.2009，這比起前面的 0.9103 小的多。

image-20240208233920437

Harnack 提出一個大膽的想法定義外容量：

用有限個區間以所有可能的方式覆蓋一個有界集合 $E$，再求每個覆蓋中各區間長度之和，並把外容量 $C_e(E)$​ 定義為最寬區間的長度趨近於 0 這種和的極限。

Pros

  • 單點 $a$ 集合的外容量為 0. 可以用長度為 $\frac{1}{k}$ 的開區間 $(a-\frac{1}{2k}, a+\frac{1}{2k})$ 覆蓋 $a$ 點。當 $k\to\infty$, 長度趨近 0。符合直覺。
  • 任何有限點集合的外容量為 0，符合直覺。
  • Harnack 可以處理一些無限點集合，如上 $S$ 集合的外容量。How？
    • 對於任何 $\epsilon > 0$, 開區間 $(0, \frac{\epsilon}{2})$ 可以覆蓋 $S$​ 中除了有限點之外所有無限點。
    • 這些有限點是 $\frac{1}{N}, \frac{1}{N-1}, …, \frac{1}{2}, 1$ 可以用一個長度為 $\frac{\epsilon}{4N}$ 的小區間覆蓋。$\frac{\epsilon}{2} > \frac{1}{N} \to N > \frac{2}{\epsilon}$
    • 因此我們可以用 $N+1$ 區間覆蓋 $S$ 集合：1 區間長度為 $\frac{\epsilon}{2}$ 和 $N$ 個長度為 $\frac{\epsilon}{4N}$ 區間覆蓋 $S$，總長度是 $1 \times \frac{\epsilon}{2} + N \times \frac{\epsilon}{4N} = \frac{3}{4} \epsilon < \epsilon$.
    • 接下來我們把最寬區間 $\frac{\epsilon}{2} \to 0$, 也就是 $N \to \infty$, 總長度 $\frac{3}{4}\epsilon \to 0$. 也就是 $S$ 的外容量 $C_e(S)$ 為 0.

Cons

  • 有界集：因爲無界集無法用有限區間覆蓋，例如所有自然數的集合，或是整數的集合。因為一開始就無法用有限個區間覆蓋。這裡區間是指有起點和終點的開區間 (a, b)。

  • 有限個區間，最寬區間長度趨近 0。所以外容量永遠為 0 ？

    • 乍看之下： $C_e(E)$ 是有限個區間的長度和，並且讓最寬區間的長度趨近於 0，也就是所有區間的長度趨近於 0 ，這是否意味 $C_e(E)$永遠為 0？ No!

    • Harnack 當然不至於犯這樣低級錯誤。竅門是當最寬長度趨近於 0，有限區間可以趨近（可數）無限區間，因此 $C_e(E)$ 可以大於 0。這有點像微積分的 L’Hopital 法則，即分子分母同時趨近於 0. 當然這也需要嚴格的數學定義。此處我們比較簡單說明。

我們再看另一個例子：R = {[0, 1] 所有有理數的集合}。

顯然這是無限多元素。根據我們宇宙酒店的例子，這是可數無限多元素的集合。

我們可以從 1 區間 [0, 1] 開始，可以覆蓋 R, 長度為 1.

當分成 2 區間覆蓋 R，可以證明無論如何分割，總長度都大於等於 1。

繼續分割成為 N 區間覆蓋 R，同樣可以證明總長度都大於等於 1。

把 N 推倒無限大讓最寬的區間長度趨於 0, 總長度仍然大於等於 1。也就是 R 的外容量 $C_e(R) = 1$​!

（集合）稠密性

R 和 S 的差別是“稠密性”。稠密性可以直觀理解為無限多元素集中的位置，或是位置 $a$ 附近 $(a-\epsilon, a+\epsilon),\text{ for any } \epsilon > 0$ 有無限多元素。例如

  • S 只有在 0 的位置有稠密性。就是在 0 附近的任意小的區間 $[0, \epsilon)$ 都包含無限多的元素。S 除了 0 以外所有的位置都沒有稠密性。
  • R 卻是在 [0, 1] 中所有的位置，例如 0.6 附近 $(0.6-\epsilon, 0.6+\epsilon)$​​ 都包含無限多的元素。R 是處處稠密！
  • 外容量就是稠密性位置的長度！！
    • S 只有在 0 是稠密性，長度為 0.
    • $R$ 是 $[0,1]$ 處處稠密，長度為 1.

我們再看一個例子 $U$ = {(0, 1) 所有無理數的集合}。

顯然這是無限多，而且是不可數的無限多元素的集合。另外 U 無理數也是處處稠密。所以 $Ce(U) = 1$

再來有點尷尬，因為我們可以定義 A = {[0,1] 所有實數的集合}

A = R + U 因為 R 和 U 互斥，聯集為實數。顯然 $Ce(A) = 1$​ 因為實數也是處處稠密。

$Ce(A) = 1 \ne Ce(R) + Ce(U) = 2$ 也就是外容量並不滿足相加性！

雖然度規 (metric) 不一定要滿足相加性，而是滿足三角不等式即可。但是否有 metric 可以滿足相加性？這對之後的應用，例如微積分有很重要的應用。

可以說 Harnack 發現有限和無限的區別，因此定義外容量甄別兩者的差別，利用的就是稠密性！稠密的位置對應無限多元素。

上界二: 測度 measure: “可數區間(不論有限或可數無限)”的長度和為 0, 稱為 measure-0，只有不可數區間才有長度！

更直觀的理解：測度 = 超級稠密性位置的長度和

Lebesgue 很敏銳的察覺上述 R 無限多和 U 無限多的基本差別！ R 是可數的無限多，U 是不可數的無限多。Lebesgue 思考是否能利用這個差別。因此他把 Harnack 的有限區間修改定義為可數區間，不論是有限還是可數無限！

關鍵的一步是把可數視為一個，不管是有限還是可數無限多。不可數的無限多是另一國！

這導致兩個結果：

  • 可以移除有界性的限制：例如自然數的集合是可數無限多，measure (長度) 為 0
  • 定義另一個度規 (metric) 就是 measure，對於有限多元素或是可數無限多 measure 都是 0, 但是對不可數無限多的 measure 不為 0. 這就是超級稠密性！

（集合）超級稠密性！

對應的稠密性也要改成一個位置 （local）附近 $(a-\epsilon, a+\epsilon),\text{ for any } \epsilon > 0$ 要有不可數無限多元素！

  • S 雖然在 0 有稠密性，但沒有超級稠密性，也就是 S measure = 0, 結果和外容量一樣。
  • R 在 [0, 1] 有理數是處處稠密，但沒有超級稠密性。也就是 R measure = 0! 這和外容量不一樣！
  • U 在 [0, 1] 無理數是處處稠密，同時也是處處超級稠密。因此 U measure = 1, 這和外容量一樣。
  • A 在 [0, 1] 實數是處處稠密，同時也是處處超級稠密。因此 A measure = 1, 這和外容量一樣。
  • 這是 measure A = measure R + measure U, 滿足相加性！

是否不可數無限多元素都是稠密的甚至是超級稠密的？ NO! Cantor Set 就是不可數無限多，但是處處不稠密或無處稠密！

康托集 (Cantor Set)

康托集是集合論和實分析中的一個經典例子，常用來說明諸如無處稠密集、完美集和不可數集等概念。它是通過反覆移除線段的中間三分之一來構造的，儘管其構造簡單，卻具有多種引人入勝的性質。

康托集的構造

  1. 從區間 $[0, 1]$ 開始: $C_0 = [0, 1]$

  2. 移除中間三分之一: $ C_1 = [0, \frac{1}{3}] \cup [\frac{2}{3}, 1]$

  3. 對剩下的每個線段重複此過程:
    • 移除 $[0, \frac{1}{3}]$ 和 $[\frac{2}{3}, 1]$ 的中間三分之一： $ C_2 = [0, \frac{1}{9}] \cup [\frac{2}{9}, \frac{1}{3}] \cup [\frac{2}{3}, \frac{7}{9}] \cup [\frac{8}{9}, 1] $
  4. 無限次重複此過程:
    • 在每一步 $n$ 中，集合 $C_n$ 包含 $2^n$ 個線段，每個線段的長度為 $\left(\frac{1}{3}\right)^n$。
  5. 康托集 $C$ 是所有這些集合的交集: $ C = \bigcap_{n=0}^{\infty} C_n $​

image-20240707222649741

康托集的性質

  1. 不可數:
    • 儘管康托集看起來”小”，但它是不可數的。這可以通過構造康托集與二進制序列集之間的雙射來證明，表明其基數與區間 $[0, 1]$ 上的實數集相同。也就是 Cantor set = $2^{\aleph_0}$
  2. 零測度 (Measure-0):
    • 在每一步中，剩餘線段的總長度相加等於 1。因此，康托集的勒貝格測度為零，這意味著它在實數線上沒有佔用任何”長度”。
    • 不僅如此，Cantor set 的外容量 = 0.
  3. 無處稠密:
    • 康托集中不包含任何區間，在實數線上的任何區間內，都有不屬於康托集的點。
  4. 完美集:
    • 康托集是閉合的（包含所有的極限點），且沒有孤立點。康托集中的每個點都是其他點的極限點。
  5. 自相似:
    • 康托集表現出自相似性；康托集的每個”部分”都是整個集合的較小副本。這一性質使康托集成為分形。
  • C 在 [0, 1] 實數是處處不稠密。因此 C measure = C outer content = 0, 測度和外容量都是 measure-0!

康托集既不是離散集合，也不是連續集合。它具有獨特的性質，使其不同於這兩個類別：

為什麼康托集不是離散集合

  • 沒有孤立點：在離散集合中，每個點都是孤立的，但在康托集中，每個點都是其他點的極限點，沒有孤立點。

為什麼康托集不是連續集合

  • 沒有區間：在連續集合中，任何小線段都包含一整個區間的點。然而，康托集是通過反覆移除每個區間的中間三分之一構造的，確保其不包含任何非零長度的區間。

總結

康托集是既非離散也非連續集合的獨特例子。它是一個完美的、完全不連通且無處稠密的集合，勒貝格測度為零。這些性質使其在實分析和集合論中成為一個重要的研究對象，特別是在分形和測度論的上下文中。

函數

從集合定義函數，類似編程所用的 key and value, $x \to f(x)$, $x$ 就是 key, $f(x)$ 就是 value. $x$ 的集合稱爲定義域，$y$ 的集合稱爲值域。函數開始有很多有趣的性質和應用。就像原子物理變成固態物理多了很多有趣的性質和應用。

函數連續性（不是前面提到的集合連續性）

直觀：一個函數在 $x$ 沒有斷點。

數學：如果函數 $f$ 在 $x$ 符合:

$\lim_{h\to 0} f(x + h) = f(x)$

則說 $f$ 在 $x$ 點連續。換句話說,如果 $h$ 趨近於 0 時 $f(x)$ 的極限存在,則 $f$ 在 $x$ 點連續。這是連續性的 $\epsilon-\delta$ 定義。

函數積分

勒貝格測度 (Measure) 一個主要的應用是積分，Lebesgue 把 measure 用於定義域分割，因為 measure 滿足相加性！這是 Lebesgue 另一個天才的發明（還是）發現。

勒貝格測度分成兩個層次：(1) 幫助確認一個函數的黎曼積分是否存在；(2) 直接定義一個函數的勒貝格積分，具有更好的性質。

黎曼/勒貝格積分

先簡單説明黎曼積分和類貝格積分的差別：

  • 非數學系學的是黎曼積分，數學系要加學勒貝格積分，因為是實變分析的基礎。

  • 黎曼微積分是分割定義域求和，勒貝格微積分則是分割值域求和。

image-20230416162150383

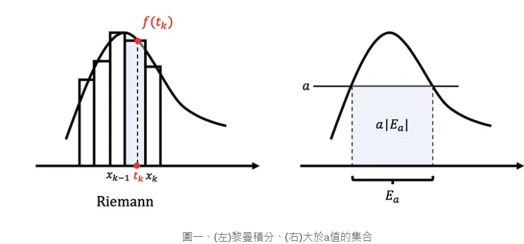
image-20240210114843831

黎曼積分

我們大學微積分學的是黎曼積分，非常直觀而且直接連結到微積分基本定理。

黎曼積分的定義：

$\int_a^b f(x) dx = \lim {n \rightarrow \infty} \sum{k=1}^n f\left(t_k\right)\left(x_k-x_{k-1}\right)$ where partition $\mathrm{P}=\left{a=x_0<x_1<x_2<\cdots<x_n=b\right}$

關鍵問題：是否任何函數的黎曼積分都存在？或是黎曼積分存在的條件是什麽？

  • 直觀而言：一個函數只要是有界 (bounded) 而且處處連續，其黎曼積分一定存在。
  • 不過直觀看，即使放寬為有限個不連續點，也不會影響黎曼積分的值和存在性。
  • 我們想要知道是若且唯若的條件 (if and only if)：勒貝格提出黎曼積分存在的若且唯若條件：不連續的點是 0-measure
  • 白話說：不連續的點(複數)不具有超級稠密性！

Lebesgue-Vitali Theorem: A bounded function on a compact interval [a, b] is Riemann integrable if and only if it is continuous almost everywhere (the set of its points of discontinuity has measure zero, in the sense of Lebesgue measure).

Ex1: Dirichlet 函數積分：$\int_0^1 f(x) dx$

$f(x)=\left{\begin{array}{l}1, \quad x \text { 是有理數 } \ 0, \quad x \text { 是無理數 }\end{array}\right.$

$f(x)$​ 是有界而且處處不連續，而且（無理數）不連續點不是 0-measure. 所以黎曼積分不存在！

我們後面會提到勒貝格積分存在！

Ex2: $f(x) = \sin \frac{1}{x}$​​ 積分從 (0, 1)

image-20240210151130669

$f(x)$ 是有界只有在 0 是無法定義 (視爲不連續?) ，其餘都是連續

假設 $1/x = n \pi \to x = 1/(n \pi)$ 在 0 附近是可數的震蕩，這是 0-measure, 所以黎曼積分存在。勒貝格積分也存在。

結果： $\sin(1) - Ci(1) \approx 0.504067$​

Ref: https://mathhelpforum.com/t/is-sin-1-x-measurable.72806/

勒貝格積分

Lebesgue measure 一開始是爲了補齊黎曼積分存在的條件而提出的。之後反而是 Lebesgue 提出新的積分概念取代了黎曼積分！接下來看勒貝格積分。

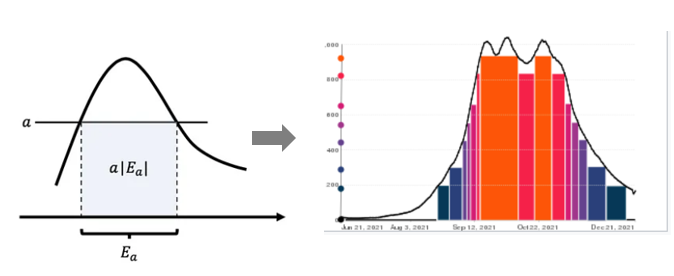
image-20240210152251046

勒貝格積分的定義和存在性： Let $R(f, E)=\left{(x, y) \in \mathbb{R}^{n+1} \mid x \in E, 0 \leq y \leq f(x)\right.$ if $f(x)<+\infty$ , and $0 \leq y<+\infty$ if $f(x)=+\infty$ } if $R(f, E)$ measurable, $\int_E f(x) d x$ exists and equals $|R(f, E)|_{n+1}$

其中 $E$ 是 $n$ 維的定義域，$f$ 是 1 維的值域。$R(f,E)$ measurable 代表 $E$ 和 $f$ 都是 measurable. $ R(f, E) _{n+1}$ 則是 1 維的實數，即是 $n+1$ 維空間的面積。

我們再看原來的 Dirichlet 函數積分 $\int_0^1 f(x) dx$

$f(x)=\left{\begin{array}{l}1, \quad x \text { 是有理數 } \ 0, \quad x \text { 是無理數 }\end{array}\right.$

  • 值域 1 的定義域是有理數：有理數是可數的無限多，可以視為可數的有限，對應的 measure = 0
  • 值域 0 的定義域是無理數：無理數是不可數的無限多，對應的 measure = 1
  • 勒貝格積分存在 : 1 x 0 + 0 x 1 = 0
  • 訣竅是把可數無限多當成可數有限多點

勒貝格積分的等價性： If $f, g \geq 0$ and measurable on $E$ and $f=g$ almost everywhere on $E$, then $\int_E f d x=\int_E g d x$

小結

  黎曼積分 勒貝格積分
可積分的連續性 不連續的點集合是 measure-0 不連續的點集合只要是 measurable 即可，不需要 measure-0
切割增加的積分單調性 不保證 100% 單調
完備性 不保證 完備
積分和極限交換性 不保證 可交換

Q&A

Q1: 有勒貝格微分嗎？No

Q2: sub-gradient optimization 和 Lebesgue 積分有關嗎？ No, 因爲是微分

附錄

函數連續性

黎曼積分與勒貝格積分之間，函數連續性的定義並無差異。連續性的正式定義在這兩種框架中都是相同的。

黎曼積分與勒貝格積分的關鍵區別在於積分的定義方式,而不是連續性的定義方式。

在黎曼積分中,積分是通過定義域分割的黎曼和的極限構造的。這需要函數在分割的定義域上連續。

在勒貝格積分中，使用值域分割對應的測度的概念定義集上的積分。這使得更廣泛的函數 (包括一些不連續函數) 可以被積分。

但是函數連續性的定義保持不變。黎曼積分和勒貝格積分都需要某種連續性概念，才能使積分存在。區別在於每種積分對連續性的具體要求。

  黎曼積分 勒貝格積分
可積分的連續性 不連續的點集合是 measure-0 不連續的點集合只要是 measurable 即可，不需要 measure-0
切割增加的積分單調性 不保證 100% 單調
完備性 不保證 完備
積分和極限交換性 不保證 可交換

黎曼 (Riemann) 可積分 vs 勒貝格 (Lebesgue) 可積分

乍看兩者的差異就是豎著切和橫著切。我不認為豎著切和橫著切本質是一樣的。雖然對於連續函數兩者的值是一樣的，但本質上的區別在於單調性，和隨之而來的完備性。

黎曼積分我們在豎著切的時候，由於我們對函數的波動起伏沒有假設，所以，每一個切片的大小都是未知的。每次細化切分/改變每段的參照點的時候，帶來的面積變化也是不固定的。

但對於勒貝格積分，由於只是在考慮單值函數下面的陰影面積，所以當我們橫著切的時候（用step function逼近的時候），我們可以保證切面的測度是隨高度單調遞減的。就像漢諾塔（或者我失敗的堆成小山一樣的午餐三明治），下面的一層總是比上面的高。所以我們每次細化切分/改變參照點的時候，面積的變化是單調的。從而單調收斂定理保證，我們總可以用簡單函數逼近得到勒貝格積分的值。而這種來自於單調收斂定理的對極限的封閉的完備性，正是我們引入勒貝格積分的重要原因之一。

  • 一般情況下涉及到具體計算都會使用黎曼積分， 況且大多數情況下他們是相等的。
  • 至於勒貝格積分的範圍比黎曼積分的範圍廣也是錯的，存在黎曼可積但是勒貝格不可積的函數，反之亦然。

從兩種積分本身的性質來看，Lebesgue積分是絕對收斂的積分，而Riemann積分不是。具體地說，我們知道，對於Riemann常義積分（定積分），可積則絕對可積，反之不對；而對於Riemann廣義積分，絕對可積則可積，反之不對。也就是說，Riemann積分意義下的絕對可積與可積是不等價的。而對於Lebesgue積分，我們知道，可積與絕對可積是一回事，也就是說，絕對可積與可積到了Lebesgue積分的意義下變成了等價關係，Lebesgue積分將絕對可積與可積統一起來。這是Lebesgue積分優於Riemann積分的一個重要區別。

從兩種積分意義下的可積函數類來看，Lebesgue可積函數構成的線性空間是完備的，而Riemann可積函數類不是完備的，也就是說，一個Riemann可積函數列的極限函數可能不再是Riemann可積的，而Lebesgue可積函數類對極限運算是封閉的。這是從函數類上看Lebesgue積分優於Riemann積分的另一個重要特點。

Reference

@shionStochasticDynamic2021

https://zhuanlan.zhihu.com/p/343129740

[@ccOneArticle23]. https://zhuanlan.zhihu.com/p/589106222 very good article!!! SDE for diffusion score

https://yrgnthu.medium.com/%E5%AF%A6%E8%AE%8A%E7%9C%9F%E7%9A%84%E8%A6%81%E8%AE%80%E5%8D%81%E9%81%8D-%E5%8D%81%E5%88%86%E9%90%98%E5%B8%B6%E4%BD%A0%E4%BA%86%E8%A7%A3%E6%B8%AC%E5%BA%A6%E8%AB%96-f5a79c9cf5a7

[@yangRealAnalysis2022]

[@kipplyTransformerInferenceArithmetic2022]

[@dunhamCalculusGallery2018]

[@yangRealAnalysisMeasurement2022]

这是一个数学无法回答的问题 #高等数学 #math (youtube.com) : 非常好的講解關於可數無窮和不可數無窮

【无痛高数】所有数都是无理数？有关无限所有困惑的答案（上）#数学 #高等数学 (youtube.com)