微積分基本定理

Posted on | In

Reference

Stokes’ Theorem on Manifolds (youtube.com) : 非常好的 lecture to combine vector calculus!

Vector calculus

Matrix calculus: The Matrix Calculus You Need for Deep Learning - Part 1 (youtube.com) for deep learning

Tensor calculus: refer to youtube, Princeton professor (Burton?)

Differential calculus: refer to visual differential calculus

Geometric algebra, GA (calculus?): refer to youtube

Takeaways

image-20240706210830528

  • 微積分可以歸納成一個基本原理：“total change on outside = sum of little changes on inside”

    • 不要小看這句話，左邊代表 global property (全域特性，例如拓撲特徵，對稱性，奇點)。右邊代表 local property (局部特性/分析，例如斜率，梯度，旋度，散度，甚至曲率)

    • 如果是有源 (source or sink)，有兩種處理方式：(1) “total change on outside = sum of little changes on inside + source/sink generation rate”; (2) 加上新的邊界把 source/sink 變成 outside. Cauchy 就是這方面的高手 (複分析)。

image-20240706210159739

  • 另一個很有深意微積分定理看法是函數的微分，變成幾何的微分。

    • 廣義 Stokes Theorem : \(\int_{\partial M} F = \int_M dF \quad \text{or} \quad \int_{\partial M} F = \int_M \partial F\)

    • 等式右邊 “sum of little change on inside” 就是 integrating a differential function on a manifold = $\int_M dF $.

    • 等式左邊 “total change on outside” 則是 integrating function along the manifold boundary = $\int_{\partial M} F $​
    • 右邊是 local property, 每一個點的特性都 count。左邊是 global property, 因爲只要管函數在 manifold edges (global) 的特性.

Q&A

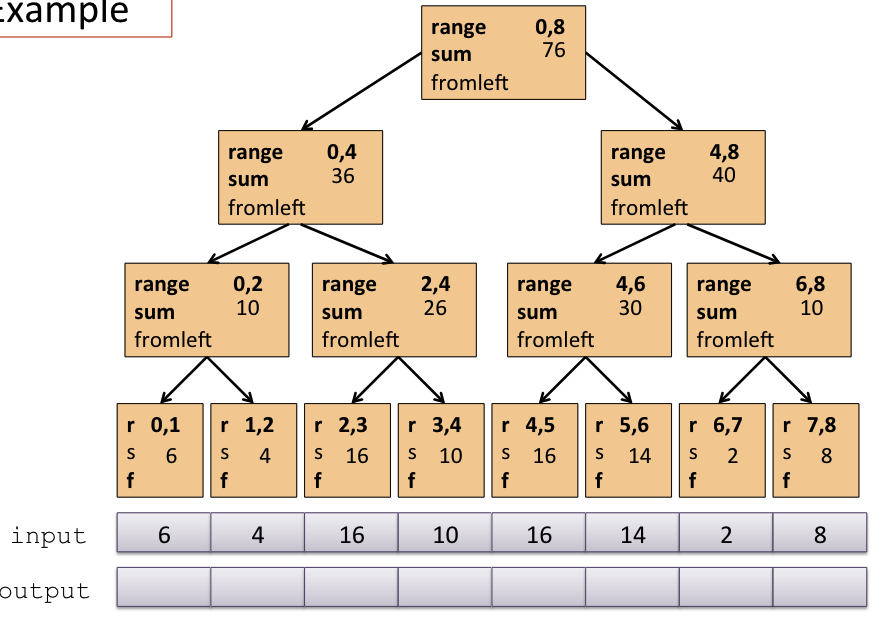
  • Discrete scan method for recursive equation 是微積分概念嗎？

image-20240511184710969

image-20240511184736495

Introduction

積分很自然，就是算面積。從幾千年前的中國和希臘就有這樣的實際需求和問題。

微分是什麽？爲什麽微分和積分牽扯在一起？

一般說微分是斜率，甚至衍生到斜率為 0 就是求極大值和極小值。

問題是斜率和積分有什麽關係。

有！就是微積分定理把算面積的積分和算斜率或是極大/小值的微分結合。這是否很不直觀？

Vector Calculus

從 vector calculus 反而可以看出微積分的基本大法！

  • 微分：就是進入無限小體積的流 - 出無限小體積的流的差，也就是無限小體積的微分的流入扣掉流出！
  • 積分：既然有流出扣掉流入，根據物質不滅定律，一定有物質在這無限小體積纍積，就是一小部分的積分。
  • 最後算總積分就是把所有無限小體積的物質都加起來。

  • 微積分定理就是内部互相抵消，只剩下頭尾的兩項。這就是基本大法。

  • Divergence 微積分對應的就是體積分變成面積分
  • Curl 微積分對應面積分變成綫積分
  • Gradient 微積分對應綫積分變成兩點的差值 （這就是大學的微積分定理）！

傳統的 Vector calculus 三大定理 (in 3D space)：

Gradient Theorem : $\int_a^b \nabla \varphi \cdot d\vec{l} = \varphi(b) - \varphi(a)$

Stokes Theorem : $\iint_S \nabla \times \vec{A} \cdot d\vec{s} = \oint_c \vec{A}\cdot d\vec{l}$

Divergence Theorem : $\iiint_V \nabla \cdot \vec{F} \,dv = \iint_S \vec{F}\cdot d\vec{s}$

image-20240331085834443

Vector field 的 divergence: 進無限小體積的 - 出體積

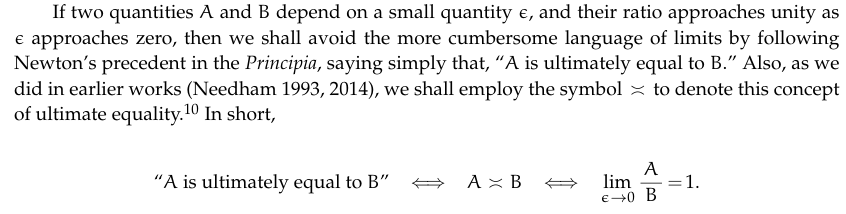
image-20240331002308055

image-20240331002348095

我們從最簡單的開始

(純量/實分析) 微積分基本定理

  • 左邊是 1D little change ($f’(x)$，導數) inside 1D line，右邊是 0D (點) 邊界

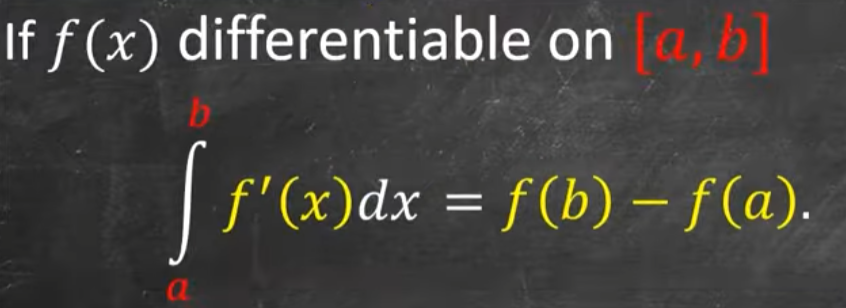
image-20240706111303014

(向量場/複分析) 微積分基本定理 (梯度)

  • 就是梯度定理。也是 Cauchy 複分析的解析函數微積分定理。

  • 左邊是 2D little change ($\nabla f$，梯度) inside 1D line，右邊是 0D (點) 邊界

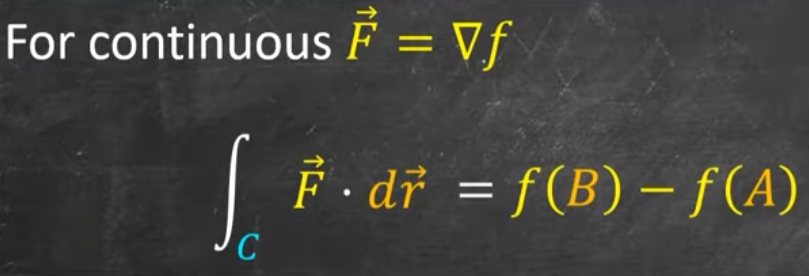
image-20240706121224013

  • 如果 y 方向是 uniform/constant field，同時綫積分沿著 y = constant 的方向，梯度定理就化簡成實數的微積分基本定理。物理解釋是内部流量的微分變化，累積成外部邊界的變化。

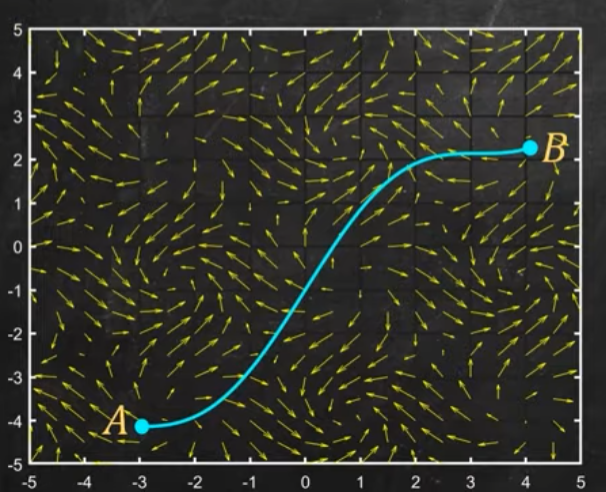
image-20240706121148287

(向量場) 微積分基本定理 (旋度)

  • Stokes 定理。右邊是 2D little change ($\nabla\times f$ ，旋度) inside 2D surface，左邊是 1D (環) 邊界

image-20240706190139797

image-20240706201047171

(向量場) 微積分基本定理 (散度)

  • Divergence 定理。左邊是 3D little change ($\nabla\cdot f$​ ，旋度) inside 3D volume，右邊是 2D (球) 邊界

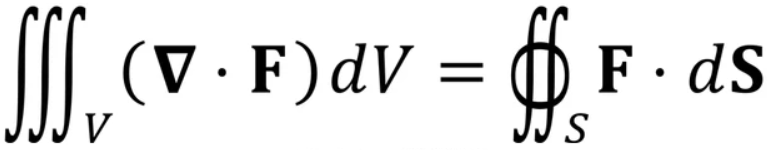
    image-20240706195015694

另一個解釋：

image-20240706225953025

Curve Space 微積分基本定理 (TBD)

Gauss Theorem on curved space \(\int A^\mu \frac{1}{6} \epsilon^{\mu \nu \rho \sigma} d S_{\nu \rho \sigma}=\int \partial_\mu A^\mu d \Omega\)

Stoke Theorem on curved space \(\frac{1}{2} \int A^{\mu \nu} \frac{1}{2} \epsilon_{\mu \nu \rho \sigma} d F^{\rho \sigma}=\int \frac{\partial A^{\mu \nu}}{\partial x^\nu} \frac{1}{6} \epsilon_{\mu \nu \rho \sigma} d S^{\mu \rho \sigma}\)

Where $d \Omega=d x^0 d x^1 d x^2 d x^3$ is the invariant spacetime volume and $d S_{\mu \rho \sigma}$ ( and $d S^{\mu \rho \sigma}$ ), $d F^{\rho \sigma}$ are 3 -surface and 2 -surface elements, respectively.

這個 “total change on outside = sum of little changes on inside” 的想法，還可以應用在任何可以内部互相抵消的應用。Gauss-Bonnet Theorem 就是一個例子。整理重點

  • 這個特性是 additive: 例如梯度，旋度，散度
  • 這個特性是可以互相抵消！

彎曲空間的基本定理 (曲率 - Gauss-Bonnet Theorem)

我們在另一個文章再展開。 \(\int_M K d A+\int_{\partial M} k_g d s=2 \pi \chi(M)\)

K 是高斯面曲率，$k_g$ 是 geodesic curvature。基本上 $K = \kappa_1 \kappa_2$。$K$ 和 $k_g$ 并不是直接微分的關係，但是

“total change on outside = sum of little changes on inside”。之後好好推導一下！

\[\begin{gathered} \mathrm{d} \hat{\mathrm{s}}^2=\mathrm{A}^2 \mathrm{~d} \mathrm{u}^2+\mathrm{B}^2 \mathrm{~d} v^2 . \\ K=-\frac{1}{\mathrm{AB}}\left(\partial_v\left[\frac{\partial_v \mathrm{~A}}{\mathrm{~B}}\right]+\partial_{\mathrm{u}}\left[\frac{\partial_{\mathrm{u}} \mathrm{B}}{\mathrm{A}}\right]\right) . \\ \mathrm{d} \hat{\mathrm{s}}^2=\Lambda^2\left[\mathrm{du}+\mathrm{d} v^2\right] . \\ \mathcal{K}=-\frac{\nabla^2 \ln \Lambda}{\Lambda^2} . \end{gathered}\]

Reference