Source
Complex Analysis L06: Analytic Functions and Cauchy-Riemann Conditions (youtube.com)
Cauchy–Riemann equations - Wikipedia
Visual Differential Geometry and Forms: Tristan Needham! Excellent Book
Visual Complex Analysis: Needham
Baidu video 半径为i的圆!三维空间是什么形状 (baidu.com)
(數學太多) Tweet of Lorentz invariant [2402.14730] Clifford-Steerable Convolutional Neural Networks (arxiv.org)
Very good video about Minkowski space: (44) Relativity 104e: Special Relativity - Spacetime Interval and Minkowski Metric - YouTube
Introduction
發現有幾個主題,我每年或每幾年都會從新學習。可以看出我對幾何最有興趣,分析次之,代數最後。代表我還是視覺動物?
-
曲面幾何:微分幾何,相對論,manifold learning,複分析其實也是幾何
-
微積分:基本/高等微積分 (Lebasque 積分/實分析/複分析,向量/張量微積分,GA (Geometric Algebra 微積分)
-
群論
之前我對複變分析都只是大學工程數學印象,用於作爲計算的工具。不過看了 Needham 的可視化微分幾何和可視化複分析。突然覺得複分析和微分幾何都是結合幾何和分析的數學。另外複平面和 Minkowski space 以及 Lorential invariant 也有密切的關係。
解析函數的數學意義
-
單值,可微分
-
(非綫性但) 保角變換
- 複分析的基石是解析函數 (analytic function)
- $f(z)$ 是 single value,例如 $z^{1/2}$ (看似廢話)
- $f(z),g(z), ..$ 都視爲 2 維複平面到另一個 2 維複平面的映射 (mapping), $z,f(z), g(z), .. \in \C $
- 可微分:$f(z) = u(x,y) + i v(x,y)$ $dw = w \, dz$ where $w = f’(z)$
-
柯西的”分析”角度:可微分的數學意義是各個方向接近 $z$ 得到同樣的極限值。可以簡化成實數軸和虛數軸接近都得到同樣的極限值。這是非常強的要求! 解析函數的數學要求是: \(\left\{\begin{aligned} \frac{\partial u}{\partial x} & =\frac{\partial v}{\partial y} \\ \frac{\partial u}{\partial y} & =-\frac{\partial v}{\partial x} \end{aligned}\right.\)
-
黎曼的”幾何”角度:$dw = w \, dz$ :$dz$ 是一個複平面上的包含各方向的小圓,$w = f’(z)$ 如果存在,是一個複平面到另一個複平面的映射 (mapping)。$dw$ 則是另一個複平面的包含各方向的小圓。$w=f’(z)$ 代表把這個小圓旋轉$\theta$,和縮放 $r$. 注意這個旋轉和縮放和小圓的各方向沒有關係,只和小圓的位置有関。代表這個變換是保角轉換。
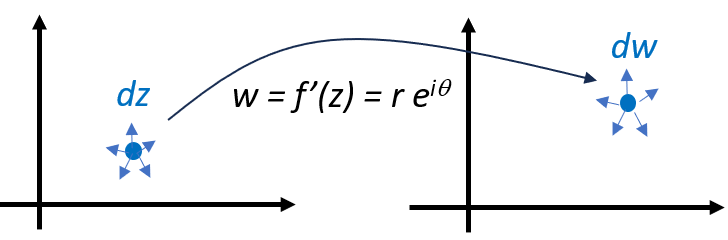
-
解析函數在微分幾何的應用是:conformal mapping (保角轉換)。在曲面 conformal map 到複數平面,經過多個解析函數變換後仍然是 conformal map!
-
99.99% 的函數都不是解析函數. 還好 polynomial function, sin/cos, exponential 都是解析函數!
- Analytic function 的 $u, v$ 都滿足 Laplace equation, 也就是 harmonic functions!
解析函數的物理意義
- (微分形式)在非奇點的地方:無旋且無源。
- (積分形式)不含奇點的回路積分為 0。含奇點的回路積分就是柯西積分。
- 解析函數的物理意義有兩種:第一種是我比較喜歡的 (因爲電機工程師的背景)

白話文: $f$ 的向量場是無旋 (Cauchy-Riemann 2nd equation, curl f = 0), 並且無源 (1st equation, div f = 0). 對應電磁理論的磁場。
-
重點是無旋無源的向量場的綫積分無奇點為 0! 但是若是綫積分包含奇點則等於 $2 \pi$! 這正是 Cauchy integral in complex analysis!!
-
解析函數的第二種物理意義:

就是解析函數都可以視爲是 potential function 的 gradient! 對應電磁學就是 $E = \nabla \phi$. E 是靜電場,$\phi$ potential field.
Potential 的 gradient 自然是無旋 (Cauchy-Riemann 2nd equation)。在無源的部分就變成 harmonic function ($\nabla^2 \phi = 0$)
我比較喜歡磁場的類比,因爲和 Cauchy integral 可以直接結合在一起。
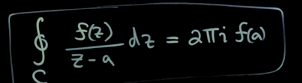
爲什麽我們在意複函數的積分?因爲 Laplace transform and Inverse Laplace Transform!

複幾何
起源與發展:
- 早期起源:複幾何的根源可以追溯到16世紀數學家如 Cardano 和 Bombelli 對複數的研究。複數的概念在18世紀被高斯進一步發展。
- 19世紀:複分析的正式研究,涉及複函數,由柯西、黎曼和 Weierstrass 開創。這奠定了複幾何的基礎。
- 20世紀:龐加萊(Poincaré)和 Cartan 的工作大大推動了該領域的發展,他們引入了來自微分幾何和代數拓撲的重要工具。後來,Kähler 和霍奇(Hodge)的工作引入了重要的結構和理論。
理論重要性:
- 數學基礎:複幾何提供了一個豐富而強大的框架,用於理解複流形、複代數簇和複解析空間的性質。
- 統一不同領域:它作為微分幾何、代數幾何和複分析等數學領域之間的橋樑。
在數學中的應用:
- 代數幾何:複幾何對理解代數曲線、曲面和高維代數簇的性質至關重要。
- 數論:來自複幾何的概念用於研究模形式和橢圓曲線,這些在現代數論和密碼學中非常重要。
- 微分方程:複微分方程及其解的研究經常依賴於複幾何的方法。
在物理中的應用:
- 弦理論:複幾何,特別是卡拉比-丘流形,在弦理論中起著基礎性作用,提供了可能的額外維度緊化形狀。
- 量子場論:各種量子場論的數學結構深深地與複幾何概念交織在一起。
在工程和計算機科學中的應用:
- 機器人學與計算機視覺:複幾何方法用於3D形狀和表面的分析與重建。
- 信號處理:來自複分析和幾何的技術應用於信號的處理和過濾。
我覺得最重要的是拓展我的思維和結合不同的應用。
複平面圓形
普通半徑為 1 的圓在實平面或複平面都非常簡單: $f(z) = \mid z \mid ^ 2 = \mid a + b i \mid ^2 = a^2 + b^2 = 1^2$
我們更有興趣是半徑為 $i$ 的圓。顯然在實平面不存在。但是在複平面存在嗎,是什麽形狀?
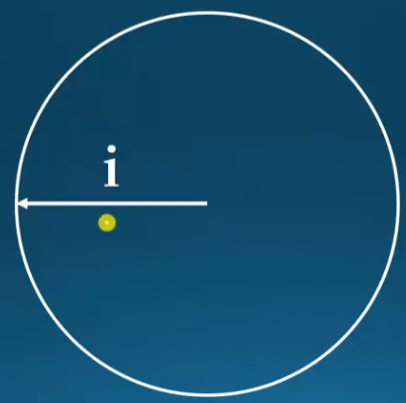
複平面或是複空間:
$(x+ i y)^2 + (a + i b)^2 = r^2$
我們 4D 投影到 3D 才看得到。所以變成
$(x)^2 + (a + i b)^2 = r^2$
$r = 1$
$(x)^2 + (a + i b)^2 = 1^2 = 1$
$(x^2 + a^2 - b^2) + 2 a b i = 1$
if $a = 0 \to x^2 - b^2 = 1$ 這是雙曲綫
if $b = 0 \to x^2 + a^2 = 1$ 這是圓形
如下圖是雙曲圓柱形, How? 不是 $a, b$ 一定要有一個為 0?
記住這是 4D 到 3D 一個角度的投影!我們要想象 $y \ne 0$ 的情況,才會得到完整 4D 到 3D 的投影:雙曲圓柱形!
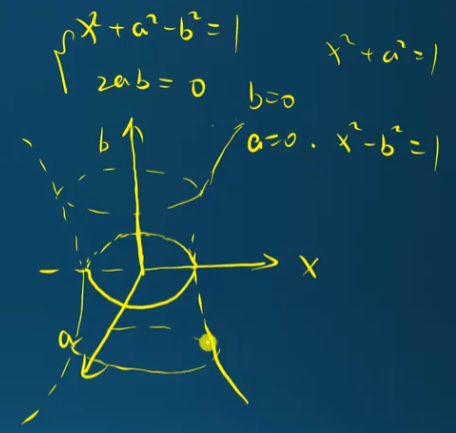
if $r = 0$
$(x)^2 + (a + i b)^2 = 0^2 = 0$
$(x^2 + a^2 - b^2) + 2 a b i = 0$
if $a = 0 \to x^2 - b^2 = 0$ 這是兩條綫
if $b = 0 \to x^2 + a^2 = 0$ 這是點
所以是完整 4D 投影到 3D 是圓錐形?
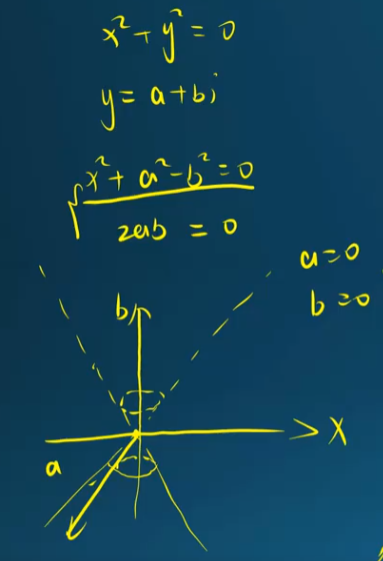
if $r = i$
$(x)^2 + (a + i b)^2 = r^2 = i^2 = -1$
$(x^2 + a^2 - b^2) + 2 a b i = -1$
if $a = 0 \to x^2 - b^2 = -1$ 這是雙曲綫
if $b=0$ 無解。所以是如下的雙曲面。可以視爲圓心在無窮遠的地方嗎?
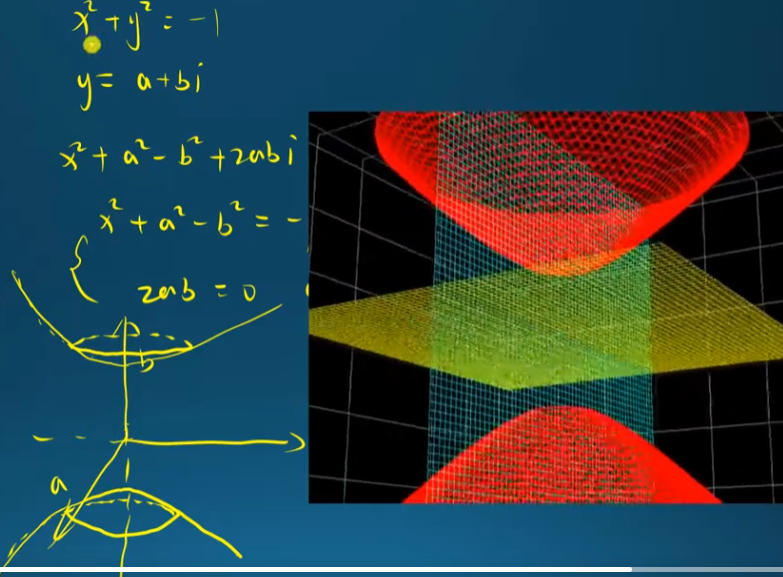
半徑為 $i$ 的圓有什麽意義?Minkowski 空間
Minkowski 空間可以看作是複半徑圓。就像單位圓是 Euclidean 空間的基本。
Euclidean 空間的物理定律,經過實單位圓的坐標轉換仍然不變,稱爲不變群 O(n).
最簡單的是 O(2), 坐標軸旋轉對於物理定律不變。
$
\begin{bmatrix}
\cos\theta & -\sin\theta
\sin\theta & \cos\theta
\end{bmatrix}
$
Lorentz Transformation and Invariance
Minkowski 空間的物理定律,經過複單位圓的坐標轉換仍然不變,也稱爲不變群, Lorentz group
$
\begin{bmatrix}
\cosh t & \sinh t
\sinh t & \cosh t
\end{bmatrix}
$
這個坐標轉換的不變性,也可以從微分幾何的第一式出發。注意 Minkowski 和 Euclidean 空間都是平直空間!
先定義 Minkowski 空間:Minkowski 空間是一個四維空間,將三維歐幾里得空間和時間結合成一個單一的流形。它用於狹義相對論理論中,具有平坦的幾何結構,其度量符號為 (-+++)。
Lorentz變換描述了兩個以恆定速度相對運動的觀察者之間事件座標的變化。它們確保了光速在所有慣性參照系中是恆定的。
在Minkowski 空間中,度量張量 $\eta_{\mu\nu}$ 定義了時空間隔:$ ds^2 = -c^2dt^2 + dx^2 + dy^2 + dz^2 $
其中 $ds$ 是不變間隔,$(t, x, y, z)$ 是座標。 Lorentz變換可以使用矩陣運算來表示Minkowski 空間中的四維向量。對於座標為 $x^\mu = (ct, x, y, z)$ 的事件,Lorentz變換 $\Lambda$ 的作用如下: $ x’^\mu = \Lambda^\mu_{\ \nu} x^\nu $ 其中 $\Lambda$ 是一個 4x4 的矩陣,滿足 $\Lambda^\mu_{\ \alpha} \Lambda^\nu_{\ \beta} \eta_{\mu\nu} = \eta_{\alpha\beta}$。 Lorentz不變性意味著時空間隔 $ds^2$ 在Lorentz變換下保持不變: $ ds’^2 = \eta_{\mu\nu} x’^\mu x’^\nu = \eta_{\mu\nu} (\Lambda^\mu_{\ \alpha} x^\alpha)(\Lambda^\nu_{\ \beta} x^\beta) = \eta_{\alpha\beta} x^\alpha x^\beta = ds^2 $ 這種不變性確保了物理定律對所有慣性觀察者都是一致的。
利用微分幾何,Minkowski 空間被描述為一個具有度量張量定義時空間隔的四維流形。Lorentz變換是保持此間隔不變的線性變換,確保了Lorentz不變性。
虛數圓的意義 ($r^2 =0$ 是光錐, $r^2 < 0$ 是光錐之内,兩個事件有因果關係,$r^2 > 0$ 是光錐之外,兩個事件無法觀察因爲超過光速 )
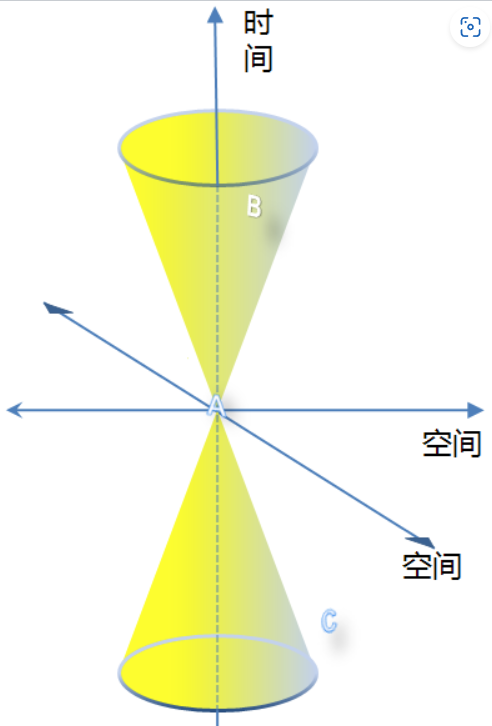
在Minkowski 空間中,兩個事件之間的時空間隔 $s^2$ 為: $ s^2 = c^2(t_2 - t_1)^2 - (x_2 - x_1)^2 - (y_2 - y_1)^2 - (z_2 - z_1)^2 $ 這個間隔可以是正的、負的或零,取決於事件在時間和空間中的相對分離。
在Minkowski 空間中,如果我們考慮一個“圓”(實際上是四維空間中的超球體),我們可能會遇到間隔為負的情況。例如,僅考慮兩個空間維度和時間:如上圖 $ s^2 = c^2(t_2 - t_1)^2 - (x_2 - x_1)^2 - (y_2- y_1)^2$
-
光錐內部的所有點(如上圖中的事件B)都可以通過小於光速的速度與當前事件建立因果聯繫,它們與當前事件的間隔被稱作類時間隔
$ s^2 = c^2(t_2 - t_1)^2 - (x_2 - x_1)^2 - (y_2 - y_1)^2 - (z_2 - z_1)^2 < 0$
-
光錐表面上的所有點都可以通過光速與當前事件建立因果聯繫,它們與當前事件的間隔被稱作類光或零性間隔
$ s^2 = c^2(t_2 - t_1)^2 - (x_2 - x_1)^2 - (y_2 - y_1)^2 - (z_2 - z_1)^2 = 0$
-
光錐外部的所有點(如上圖中的事件C)都無法與當前事件建立因果聯繫,它們與當前事件的間隔被稱作類空間隔
$ s^2 = c^2(t_2 - t_1)^2 - (x_2 - x_1)^2 - (y_2 - y_1)^2 - (z_2 - z_1)^2 > 0$
當然這和 Minkowski 空間的定義有關,如果是定義 (+,-,-,-), $s^2$ 的正負就剛好相反。