拉格朗日力學 - Lagrange Mechanics

Posted on | In

Lagrangian Lagrange multiplier, Legendre transform, Hamiltonian

Reference

https://www.youtube.com/watch?v=drZGeAkN4QI&ab_channel=PhysicsFluency : Excellent Youtube video!

拉格朗日力學

用三個數學式就可以説明拉格朗日力學：

  • Lagrangian 的定義
  • 最小作用原理。S 是 L 對時間的積分。
  • Euler-Lagrange 公式，來自於最小作用原理。

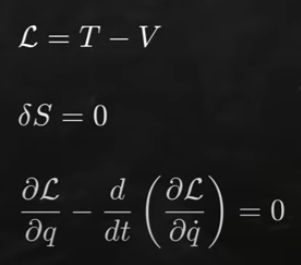
image-20240413202238269

拉格朗日力學的兩個疑惑

  1. 爲什麽定義 L = T - V? 而且對應最小作用？
  2. 爲什麽可以使用不同廣義坐標系都有最小作用，and Euler Lagrangian equation?

比較起來

  1. 爲什麽有最小作用原理: 大哉問，神的創造是節省的！
  2. 推導 Euler-Lagrange equation ： 只是技術活

爲什麽 L = T - V = kineTic Energy - potential (Vires) Energy?

物理兩個最基本例子： (1) 自由落體 (固定加/減速度運動)；(2) 簡諧運動 (加速度和位移正比)

我們一自由落體運動爲例：

image-20240413211520338

重點是 Energy space (T, V 軸)

物理有三個圖: (Motion) x-t: 位移 vs. 時間圖 (最常見)； (Phasor) p-x: 動量 vs. 位移圖 (最常用於 Hamiltonian 物理)；Energy space (T vs. V) 圖 (好像很無聊，如果沒有時間的話)

沒有時間的 energy space, 不是唯一的軌跡！

先看沒有時間的 energy space 圖如下：因爲能量守恆 $E_t$, total energy，所有的運動都是在 -45 度的斜綫上移動。

**此時我們要發揮想象力：把 E 視爲一個 vector, 大小是 E scalar, 而不只是 scalar! **

第一種分解 (T, V)：T T^ + V V^ = Et

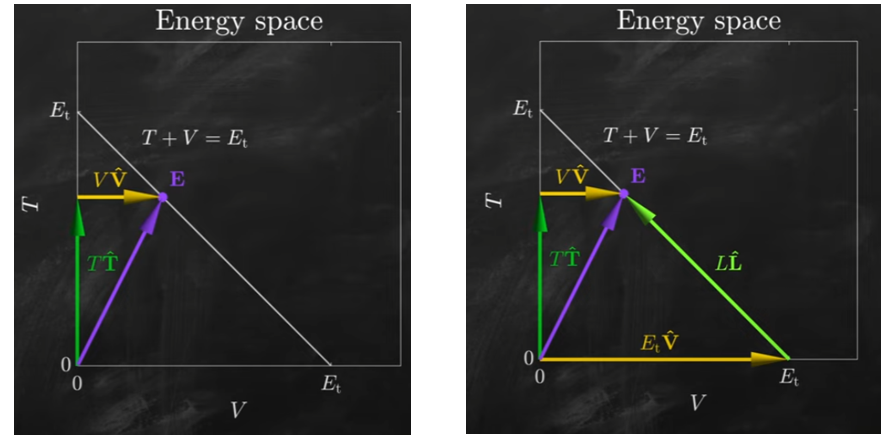
image-20240413212139379

我們可以用另一種分解 (V^, L^)：

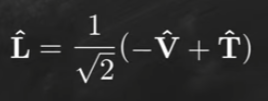
image-20240413212711614

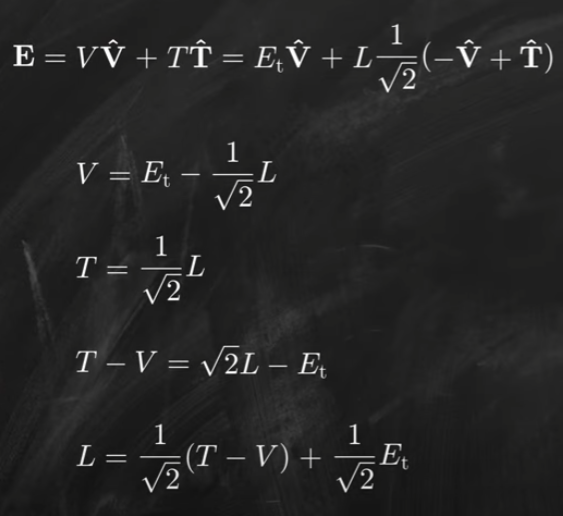
image-20240413213355150

包含時間的 Energy Space 是最小作用原理和廣義坐標的關鍵！

Energy space 最重要還是要有時間維度。所有可能的運動軌跡都要滿足能量守恆。所以都必須在這個平面上。任何這個平面的規矩能量都守恆，但是 Lagrangian 隨時間的變化的不同。

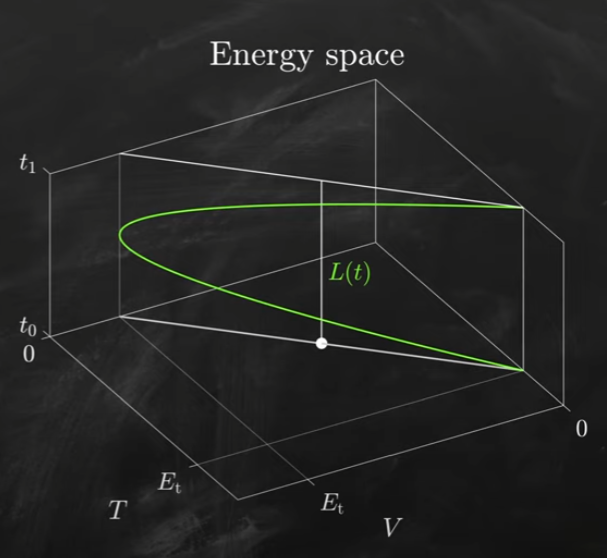
image-20240413214300522

接下來可以對不同的坐標系 L to T or L to V 投影。如下圖。

可以看出形狀一樣，只是以 L 為鏡子。這是為廣義坐標鋪路？

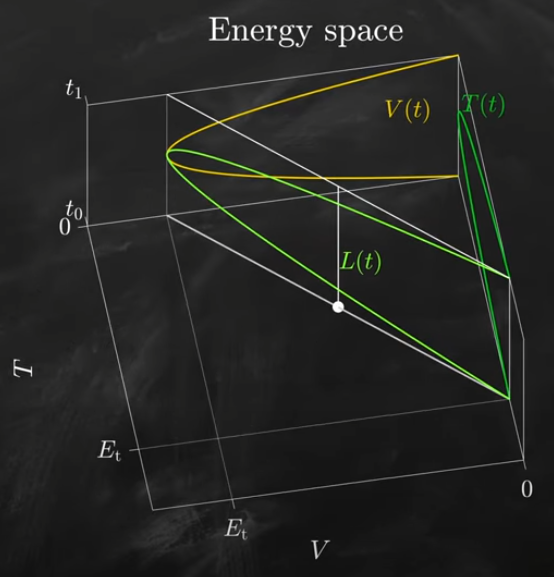
image-20240413222857925

有兩個 assertions!

  1. 包含時間的 energy space 的軌跡唯一決定物體的運動！不然和古典物理的決定論抵觸。
  2. 這個唯一的軌跡滿足最小作用原理！這是神跡！

最小作用原理

image-20240413214641360

利用 Euler-Lagrange equation.

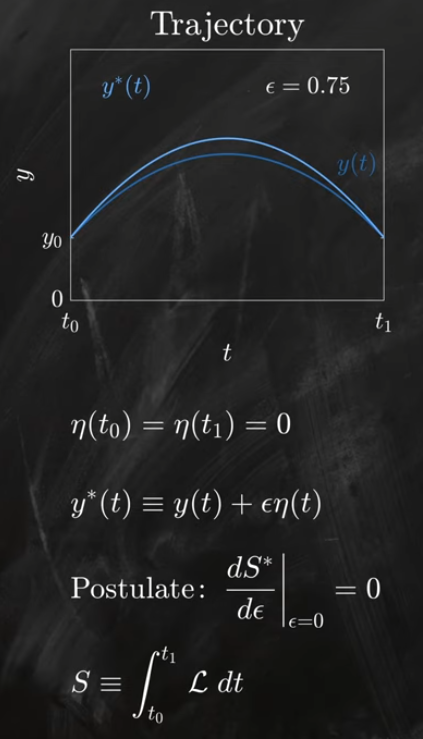
image-20240413224331024

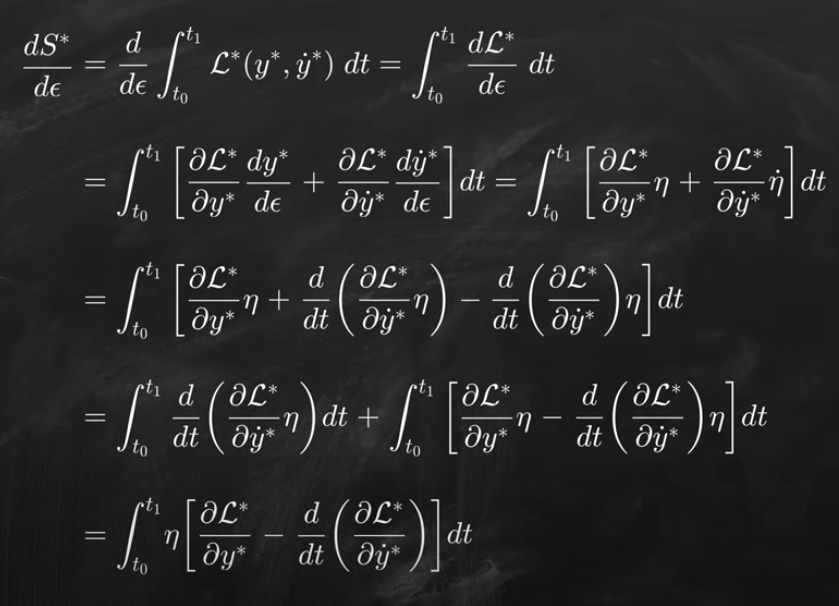
image-20240413224421083

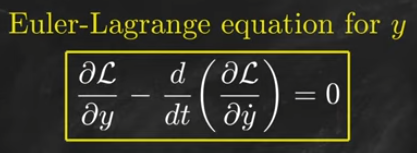
image-20240413224522096

廣義坐標系

好像還是不明白？用單擺的 $y, \dot{y}$ 或是 $\theta, \dot{\theta}$ 做為例子？同樣回到上述的兩個 assertions!

  1. 包含時間的 energy space 的軌跡唯一決定物體的運動！不然和古典物理的決定論抵觸。
  2. 這個唯一的軌跡滿足最小作用原理！這是神跡！

我們同樣可以畫出 energy space with time 的軌跡圖。同樣也用上面的變分法。

  1. 一定沒有問題，不同的坐標的 degree of freedom 一樣，只是不同的 bases (可以是 nonlinear mapping).

  2. 我就不確定不同坐標系是否都有一樣的最小作用原理？應該是。