曲率

Posted on | In

Source

Visual Differential Geometry and Forms: Tristan Needham! Excellent Book

Takeaway

  • 幾何的重點是在找到坐標無關的 invariant properties!

  • Intrinsic (主流) vs. extrinsic
  • Local vs. global
  • Flat vs. Curved

外視通常稱爲上帝視角。内視是空間生物可以看到或是測量的量

之前我的 bias 都是從 extrinsic 外視開始，再思考 intrinsic 内視。這是歷史的軌跡。

其實比較自然是從 intrinsic 開始，例如我就是在 3D intrinsic space.

  • 1D intrinsic 例如蚯蚓
  • 2D intrinsic 例如螞蟻
  • 3D intrinsic 例如人

在從 intrinsic 擴展到 extrinsic space by adding 1 more dimension.

  • (intrinsic) 對於 1D 蚯蚓，只有前進和後退，沒有曲率的觀念。
  • (extrinsic) 1D + 1D = 2D
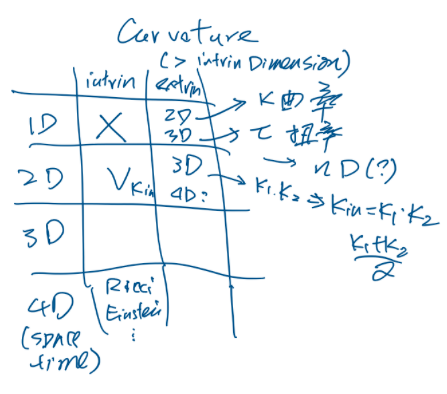
  Intrinsic Extrinsic, embedded in higher dimension
1D X 2D: k (曲率)；3D: tau (扭率) ； nD?
2D Kin 3D: K1, K2 (Kin = K1*K2)；4D?
3D    
4D Ricci K, Einstein K  
nD    

Flat vs. Curved vs. Topology

平直空間 (Flat Space): 內視 (面?) 曲率為 0 的空間

image-20240701114821547

平直空間 (Flat Space) 包含 Euclidean and Minkowski space.

平直空間的定義就是每一點的 metric 都一樣 (保距和保角)。

Euclidean Invariant:

  • Euclidean distance and angle! (Isometry) 不管用什麽坐標 (卡式或極坐標) 兩個點 (事件) 之間的 distance and angle 不變 (保距和保角)。物理上就是剛性旋轉 (cos and sin matrix) transformation invariant。數學上就是 Euclidean space 的 eigen-vectors 就是直角坐標系。

Minkowski Invariant:

  • Lorentz invariant! 不管用什麽坐標 (卡式或極坐標) , “保距和角度” 不變。
  • 不過這裏的距離是 ($s^2 = (ct)^2 - x^2$)。 這裏的角度是 cosh and sinh 轉換！
  • 物理上就是兩個點 (事件) 的光速不變。數學上就是 Lorenz invariant. Minkowski space 的 eigen-vectors 就是 x= ct?
  • Lorentz transformation 就是“剛性旋轉”！！

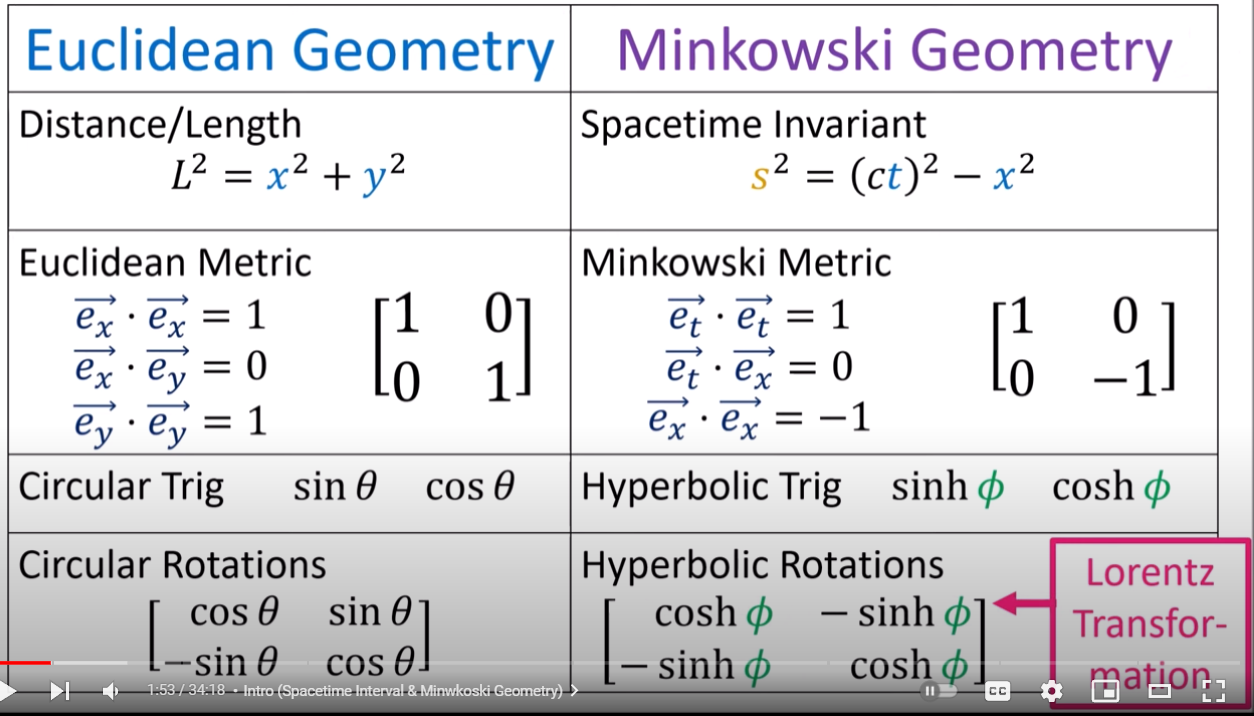
image-20240623225048468

Relativity 104e: Special Relativity - Spacetime Interval and Minkowski Metric (youtube.com)

image-20240623214037875

Curved space:

Invariant:

  • (弧長) 就是 ds^2 = A dx^2 + 2B dx dy + C dy^2. A, B, C 和 metric 有関，是 location dependent。基本和 local 有関。 Euclidean and Minkowski invariant 都是其特例。
  • (曲率)：Flat space 的曲率 = 0，是 invariant 的特例。Curve 空間重要的 invariant 應該是曲率。問題什麽是曲率？

Topological space:

Topological space 基本都是 global. 重要的 invariant

Invariant

  • Euler characteristic ($\chi = 2 - k$) : k 是虧格數。Euler characteristic 是拓撲不變量。2 是 3 D 體。如果是 2D 平面，1-k.

  • Local and global link? Gauss-Bonnet 定理！！ image-20240701114540939

    • 注意，以上第二項的綫積分包含不連續轉角（外角）和！
    • K 是高斯面曲率，內視和外視都一樣 (絕妙定律)。$\kappa_g$​​ 是 geodesic 線曲率，是曲面上的內視線曲率。Euler characteristic 應該是內視？所以 Gauss-Bonnet 是內視？
    • Gauss-Bonnet 其實是三角形内角和為 $\pi$​​ 的推廣！
    • Geodesic Triangle ($\alpha$ 是内角)

    image-20240701225057329

    • 半球形 (圓形沒有内角)

    image-20240701225840070

    • 圓形 (圓形沒有内角)

image-20240701231000135

內視和外視曲率

image-20240701114745170

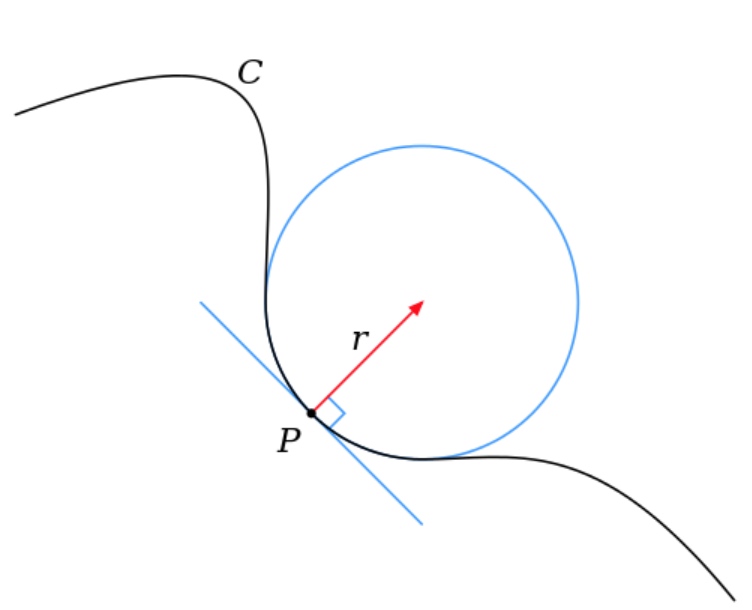
一維曲綫在二維平面的外視線曲率

一維曲綫内視只有前進和後退，沒有内視曲率。當然這是從幾何角度來看。如果從物理角度，一個人坐雲霄飛車，即使閉著眼睛 (模擬一維空間) 還是可以感受前進，後退，和曲率。

因爲曲綫可以任意彎曲，我們只定義外視曲率。先考慮外視空間是二維歐氏平面上的一維曲線。很明顯曲線上每一點（和其鄰近點）都可以定義“線曲率” $\kappa$ 是相切圓（不是拋物線!）半徑的倒數，i.e. $\kappa = 1/r$. 當然可以根據相切圓是在曲線的上方或是下方定義 $\kappa$ 是正或是負。$\kappa$ 明顯和泰勒展開的二階導數成正比1。直線的二階導數為 0, 曲率為 0.

image-15696871816594

幾何的角度 (T 是單位切向量，N 是單位法向量)：

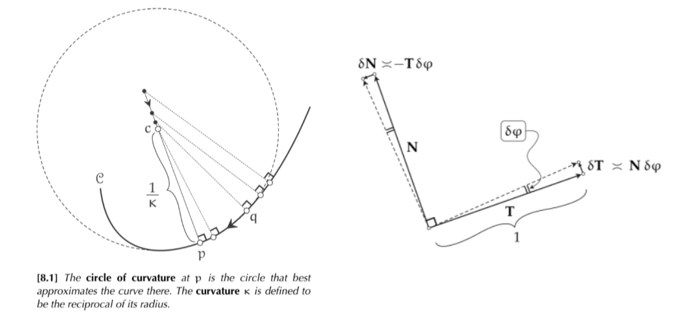
image-20240630221214282

對於曲綫曲率一個更好的定義是單位弧長的角度變化：$\kappa =(\mathrm{d} \varphi / \mathrm{ds}) $​. 這裏的 $\varphi$ 是和 x 軸的夾角。 \(\mathbf{T}=\left[\begin{array}{l} \cos \varphi \\ \sin \varphi \end{array}\right] \quad \text { and } \quad \mathbf{N}=\left[\begin{array}{r} -\sin \varphi \\ \cos \varphi \end{array}\right]\)

由 T 和 N 對弧長的微分：

\[\begin{gathered} \frac{\delta \mathbf{T}}{\delta \mathrm{s}} \asymp \mathbf{N} \frac{\delta \varphi}{\delta \mathrm{s}} \Longrightarrow \frac{\mathrm{d} \mathbf{T}}{\mathrm{ds}}=\kappa \mathbf{N} . \\ \frac{\mathrm{d} \mathbf{N}}{\mathrm{ds}}=-\kappa \mathbf{T} . \\ \end{gathered}\]

牛頓定律

以上弧長微分很容易變成時間微分。只要定義固定速度 $v$： \(\begin{aligned} & \delta s \asymp v \delta t \text { and } \mathbf{v}=v \mathbf{T} . \\ & \mathbf{F}=\mathrm{m} \frac{\mathrm{d} \mathbf{v}}{\mathrm{dt}}= m \frac{v \,d\mathbf{T}}{\mathrm{dt}} = m \frac{v \kappa \boldsymbol{N}\,ds}{\mathrm{dt}} = \kappa \mathrm{m} v^2 \mathbf{N} . \end{aligned}\)

向心力等於動能乘以曲率。

一維曲綫在三維平直空間的外視參考坐標：Frenet Frame : 線曲率+線撓率

對於一維曲綫只有曲率向量 $\kappa\boldsymbol{N}$，對應牛頓力學的向心力方向。在三維空間的自由綫，還擴展出一個撓率 $\tau$ 對應曲率向量在垂直於 $\boldsymbol{T}$和 $\boldsymbol{N}$ 構成平面外的抖動。稱爲 Frenet-Serret 微分公式：此處的微分是對於弧長。 \(\left[\begin{array}{l} \mathbf{T} \\ \mathbf{N} \\ \mathbf{B} \end{array}\right]^{\prime}=\left[\begin{array}{rrr} 0 & \kappa & 0 \\ -\kappa & 0 & \tau \\ 0 & -\tau & 0 \end{array}\right]\left[\begin{array}{l} \mathbf{T} \\ \mathbf{N} \\ \mathbf{B} \end{array}\right]=[\Omega]\left[\begin{array}{l} \mathbf{T} \\ \mathbf{N} \\ \mathbf{B} \end{array}\right]\)

下圖的 $e_1 = \boldsymbol{T}$, $e_2 = \boldsymbol{N}$, $e_3 = \boldsymbol{B}$

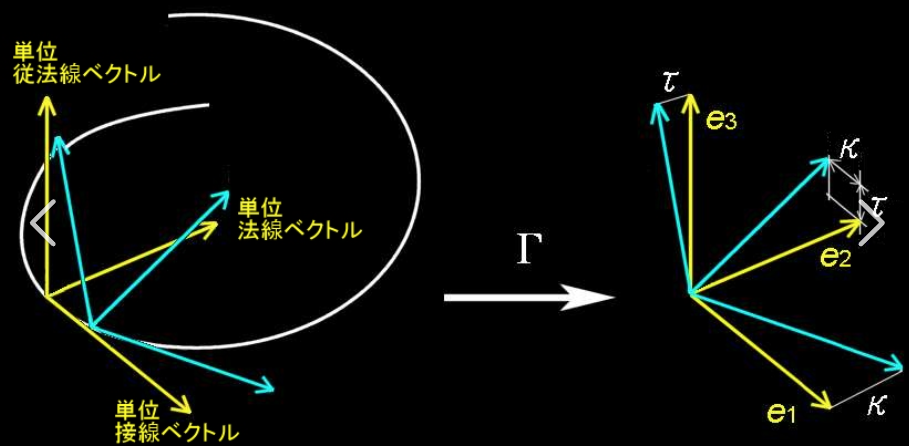
image-20240713201326814

我覺得 Frenet frame 基本沒有太大的用途。因爲是以曲綫本身的視角的 frame. 每條曲綫都有自己的 frame, 沒有統一的 reference frame，所以沒什麽用。

Frenet Frame vs. 切平面 Frame

一般我們有興趣的曲綫是在一個曲面上，而不是 free style。曲綫可以亂畫，曲面只有一個。因此用曲面做為參照坐標系 (reference frame) 才有意義。嚴格的說，是曲面每一點的切平面的 (local) 坐標系。

例如下圖的曲綫 C on 曲面 S。在 p 點的切平面 $T_p$

  • 下圖的曲綫 C 在 p 點的切綫向量 $\boldsymbol{T}$ 和上圖 Frenet frame 的 $e_1 = \boldsymbol{T}$ 是同一個向量。切綫向量落在切平面 $T_p$ 上。
  • 下圖曲率向量 $\boldsymbol{\kappa}$ 對應上圖 Frenet frame $\kappa \boldsymbol{N}$ （$\boldsymbol{T}$ 的微分），也就是 $\boldsymbol{\kappa} = \kappa \boldsymbol{N}$。曲率向量一般不會在切平面 $T_p$​ 上。
  • Frenet frame 是用 $\boldsymbol{T}$, $\boldsymbol{N}$, 以及 $\boldsymbol{N}$ 的微分產生的 $\boldsymbol{B}$, 作爲基底向量。微分幾何卻是把曲率向量進一步分解，所有相似止步於此。
  • 下圖還有 S 的切平面 $T_p$ 作爲 reference, 可以進一步把曲率向量分解成垂直和平行於 $T_p$ 的分量 $\boldsymbol{\kappa} = \boldsymbol{\kappa}_g + \boldsymbol{\kappa}_n$ 。 這裏和 Frenet 分道揚鑣了。此處的 $\boldsymbol{n}$ 是垂直於 $T_p$ 的向量，和上圖的 $\boldsymbol{N}$ ($\boldsymbol{T}$ 的微分) 完全無關！

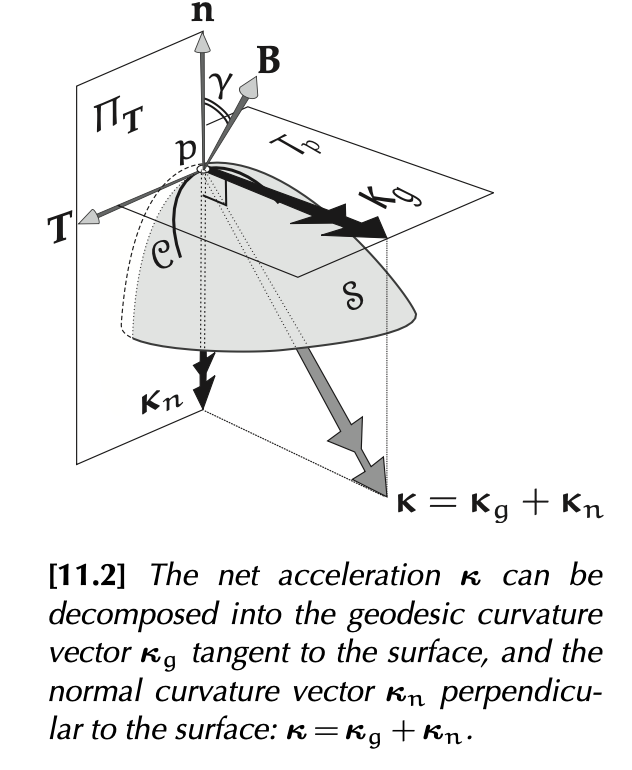
image-20240710220648371

Frenet Frame: ($\boldsymbol{T}$, $\kappa \boldsymbol{N}$, $\boldsymbol{B}$​) 如上圖

切平面 $T_p$ Frame: ($\boldsymbol{T}$, $\boldsymbol{\kappa}_g$, $\boldsymbol{\kappa}_n = \kappa_n \boldsymbol{\hat{n}}$) 如上圖

$\boldsymbol{T}$ 和 $\boldsymbol{\kappa}_g$ 组成 $T_p$ 如上圖。$\boldsymbol{\hat{n}}$ 是 $T_p$ 的 normal，和 $\boldsymbol{N}$ 無關。

如果 C 曲綫的 $\boldsymbol{\kappa}_g = 0$ 稱爲 geodesic.

接下來，我們再進一步對 $\kappa_n$​ 加以分解。

一維曲綫在二維曲面的外視線曲率 I - 法向量面交綫

再回到二維曲面，曲面上每一點都有無限條曲面上的曲線相交於這一點。每一條曲線都有本身的“線曲率”，可以是正或負。

Euler 發現二維曲面和相交該點 P 所有法向量面的綫曲率 (其實是 P 點所有的 geodesics) 的曲率是： \(\kappa_n(\theta)=\kappa_1 \cos ^2 \theta+\kappa_2 \sin ^2 \theta .\) 高斯曲率 $R$ 剛好是最大線曲率乘最小線曲率（含正負號）, i.e. $R = \kappa_1 \kappa_2$; $\kappa_1$ 是最大線曲率；$\kappa_2$​ 是最小線曲率。高斯曲率非常重要，這是二維曲面的内視曲率。也就是内視生物可以看到或是測量出的曲率，剛好等於外視曲率 $\kappa_1\cdot \kappa_2$。高斯稱爲絕妙定理。但是内視的生物無法看到 $\kappa_1$ 或 $\kappa_2$ 或是兩者的平均曲率。

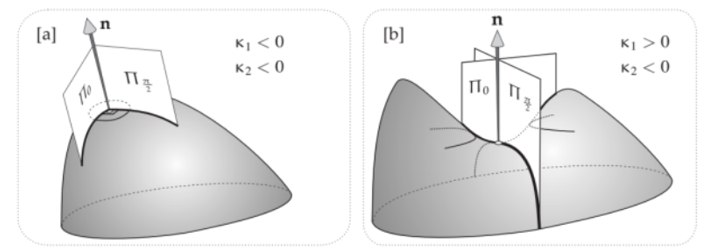
image-20240630224346654

以完美球面為例，每一點所有相交曲線的線曲率都一樣。都是大圓（圓心即是球心）半徑的倒數。所以球面每一點的高斯曲率 $R = \kappa_1 \kappa_2 = 1/R^2$. 這符合直覺。

如果是非完美球面，例如橢圓球面半徑為 $(a, b, c)$, 曲面每一點的高斯曲

率都不同，還是可以找到對應的 $\kappa_1 \,, \kappa_2$. （完美或非完美）球面上同一點 $\kappa_1 \,, \kappa_2$一定同正或同負，所以橢圓幾何每一點的高斯曲率為正！

再考慮雙曲幾何。每一點相交曲線的”線曲率“必定有正有負，$\kappa_1 > 0 \,, \kappa_2 < 0$. 所以雙曲幾何每一點的高斯曲率為負！

一維曲綫在二維曲面的外視線曲率 II - 任意綫

就是人在地球上的情形。任意一條地上的曲綫包含了曲綫在局部平面的曲率 ($\kappa_g$， 代表 geodesic curvature)，以及地球本身的曲率 ($\kappa_n$)，如下圖 $\boldsymbol{\kappa} = \boldsymbol{\kappa}_g + \boldsymbol{\kappa}_n$ 向量。 $\kappa_g$ 就是用一個平面圓逼近，或是平面弧度的變化。$\kappa_n$ 則是曲面本身的外視線曲率，就是上面的 $\kappa(\theta)$ ($\kappa_n \ne 1/R^2 = \kappa_1 \kappa_2$?) R 是面曲率。

注意 $\kappa_g$ 是二維生物可以測量的，也就是内視線曲率。但是 $\kappa_n = \kappa(\theta)$ 不是内視線曲率。只有在特別的例子，例如球體可以從高斯曲率開根號得到！

image-20240630231724208

  • 如果一條曲綫每一點 $\kappa_g = 0$， 則是 geodesic! 白話文：如果一條線每一點的 geodesic curvature 為 0, 這條線就是 geodesic (曲面上的直線！)。這是可以內視的性質。

二維曲面在三維空間的外視面曲率

二維曲面在四維空間的內視面曲率

Ricci Tensor? 黎曼曲率

Connection

Machine Learning and Manifold Learning (Output or Parameter?)

Analytic ML: Low D to high D (embedding) 再 low D (encode): SVM, …

Feature extraction: high D (image) to low D (encode): classification

Generative AI: high D (image) to low D (encode) then to high D (decode)

image-20240623221611830

Generalization：内插 (同一 dimension), 外插 (同一 dimension), 外插 (to high dimension)

内插: 用傳統算法也 OK.

外插到一個 dimension ：只是内插的延申。傳統算法和 NN 都 OK.

外插到 high dimension! 只能靠 ML, 用 data 來 train. 除非有 prior 知道 high dimension 才有機會用傳統算法。

Manifold learning hypothesis: 是 data 在 low dimension manifold. 但是可以推論 NN 的 parameter space 也是在 low dimension manifold? (例如 sparsity)

image-20240623222105325

Intrinsic Surface Curvature (内視面曲率)

幾個重點：

內視面曲率定義

  • 用三角形角度 angular excess (0th-order): 最通用，可以拓展到 n 多邊形。分母是面積，比例是 $r^2$

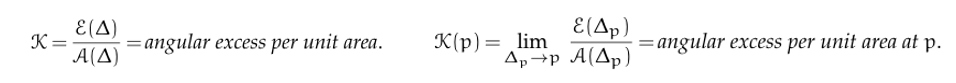
    image-20240330101412604

    where \(\mathcal{E} \equiv(\text{angle sum of triangle})-\pi .\)

  • 用圓形周長 excess (1st-order): 是近似，極限相等。分母是 $r^3$

image-20240330101851574

  • 用圓形面積 excess (2nd-order): 是近似，極限相等。分母是 $r^4$

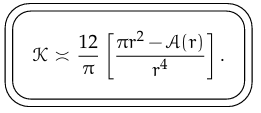
image-20240330102011396

  分子 分母 比例常數
  三角或多邊形角度 excess $r^2$ 1
  圓形周長 excess $r^3$ $3/\pi$
  圓形面積 excess $r^4$ $12/\pi$

Map

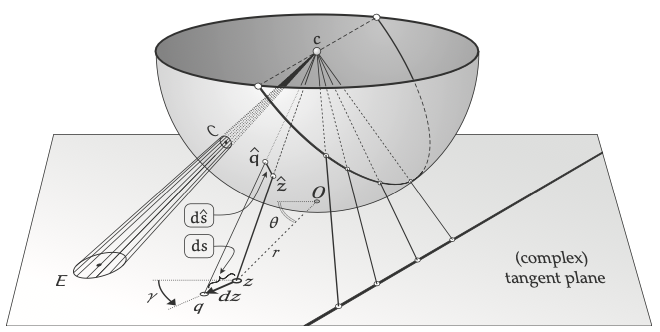
image-20240401213118272

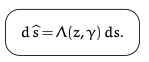
image-20240401213438252

Metric vs. Curvature

簡單說就是

  • 知道每一點的 metric 就完全知道這個曲面
  • 可以說知道每一點的 curvature 就完全知道這個曲面嗎?
  • Curvature (K) 基本是 metric (A, B) 的兩次微分

image-20240401213553013

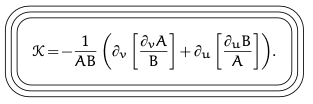
image-20240401213634743

以下的 mapping 是 conformal mapping

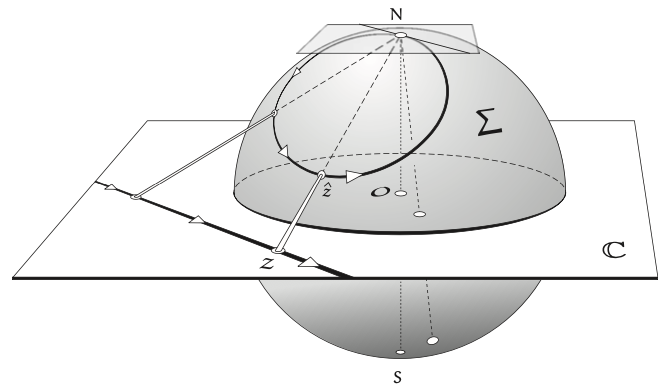
image-20240401213241313

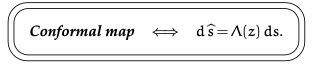
image-20240401213932762

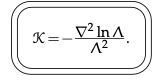
image-20240401213950528

$\Lambda$ 基本就是 metric. 兩次微分基本是 Gaussian curvature.

Creator 黎曼幾何 歐氏幾何 羅氏幾何
(Global) 曲面形狀 橢圓球面 平面 雙曲面
(Global) 高中平行公理：直綫外一點有幾條直綫不相交 0 1 $\ge 2$
(Global) 三角內角和 A > 180 A = 180 A < 180
(Global) 圓周率 $<\pi$ $\pi$ $>\pi$
(Global/local) Holonomy: PT 沿著 close loop 的角度差 H > 0 H = 0 H < 0
(Global/local) Independence of PT (!PT): PT 在任兩點相同和軌跡無關 No Yes No
(Local) 2D 高斯曲率純量: $R = \kappa_1 \kappa_2$ $R > 0$ $R = 0$ $R < 0$
(Local) 黎曼曲率張量: $R^a_{bcd}$ $R \ne 0$ $R = 0$ $R \ne 0$
(Local) Ricci 曲率張量: $R_{\mu\nu}$ $R \ne 0$ $R = 0$ $R \ne 0$
(Local) 連結 (connection): $\Gamma$? $\Gamma \ne 0$ $\Gamma = 0$ $\Gamma \ne 0$

Introduction

發現有幾個主題，我每年或每幾年都會從新學習。可以看出我對幾何最有興趣，分析次之，代數最後。代表我還是視覺動物？

  • 曲面幾何（非常頻繁）：微分幾何，相對論，manifold learning
  • 微積分（頻繁）：基本/高等微積分 (Lebasque 積分/實數分析，向量/張量微積分，GA (Geometric Algebra 微積分)
  • 群論（不頻繁）

image-20240330084753057

[1.8] Harriot’s Theorem (I603): $\mathcal{E}(\Delta)=\mathcal{A}(\Delta) / R^2$. Adding these last three equations, we find that \(3 \mathcal{A}(\Delta)+\mathcal{A}\left(\Delta_\alpha\right)+\mathcal{A}\left(\Delta_\beta\right)+\mathcal{A}\left(\Delta_\gamma\right)=2(\alpha+\beta+\gamma) \mathrm{R}^2 .\)

Finally, subtracting (1.4) from (1.5), we find that \(\mathcal{A}(\Delta)=R^2(\alpha+\beta+\gamma-\pi)=R^2 \mathcal{\varepsilon}(\Delta),\)

In both Spherical and Hyperbolic Geometry, \(\mathcal{E}(\Delta)=\mathcal{K} \mathcal{A}(\Delta),\) where $\mathcal{K}$​ is a constant that is positive in Spherical Geometry, and negative in Hyperbolic Geometry.

Gauss-Bonnet Theorem (不只結合 local/global, 同時連結 Geometry/Topology)

https://en.wikipedia.org/wiki/Gauss%E2%80%93Bonnet_theorem

image-20240401095510432

如果是 Geodesic Triangle:

image-20240401095605470

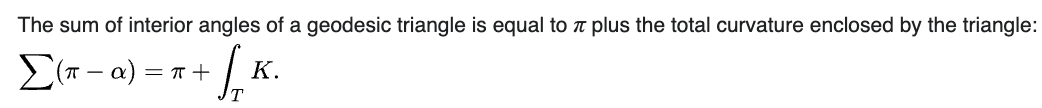
image-20240401095704958

幾何根據全域或局部以及外視或内視可以略分為 4 類：

  • Local (局部): 基於非常小區域 (微分=無窮小) 的特性，例如曲率 (curvature)、connection (covariant derivative)

  • Global (全域): 基於 loop、transversal (軌跡)、大區域的特性，例如圓周率、三角形内角和、曲面的形狀
  • Extrinsic view (外視): birds-eye-view (上帝視角) 即是 manifold 是嵌入更高維的歐式空間 (X, Y, Z 卡氏座標)
  • Intrinsic view (內視): bugs-eye-view (毛毛蟲視角) 沒有參照坐標系，只能靠 manifold 本身的 objects (綫，角度，平行移動) 推導 manifold 的性質。結果應該和 extrinsic view 結果一致。

一個的例子説明不同的方式定義“直綫”。

直綫 Extrinsic (Birds-Eye-View) Intrinsic (Bugs-Eye-View)
Global (大區域) 兩點之間最短“歐氏距離” 但限制在曲面上 兩點之間最短“度規距離” (metric distance)
Local (非常小區域，微分) Acceleration vector (position vector 的二次微分) 的切平面的分量為 0 平行移動 (Parallel transport) 和此綫的切向量同向

更多 (但不完整) 的比較。

  Extrinsic (Birds-Eye-View) Intrinsic (Bugs-Eye-View)
Global (大範圍) 1. X,Y,Z 卡氏座標
2. Position vector, $\vec{R}$		 廣義相對論
Local (非常小範圍，微分) 1. Basis vector: $u=\frac{\partial \vec{R}}{\partial x}, v=\frac{\partial \vec{R}}{\partial y}$
2. Mean curvature		 1. 切平面，切向量 basis vector
2. Gaussian/Riemann curvature

非歐幾何關鍵：平行公理

垂直和平行都是幾何最重要的基石。

  • 垂直的局部性質 (角度) 很直接，兩直線相交，夾角為 90 為垂直。一般人隨手可以畫出垂直相交線，即使在曲面也不例外。垂直的微分定義是兩直線切向量內積為 0.
  • 平行的概念看似直接，兩直線永不相交，這是一個全域性質。在歐幾里德平面幾何很容易想像。兩個問題：(A) 這樣平行直線唯一嗎？或一定存在嗎？ (B) 平行是否有局部的微分定義？

(A) 的回應就是平行公理；(B) 的回應就是平行移動 (parallel transport).

(A) 平行公理有幾種不同形式：

  • 歐幾里德平面幾何五大公理，最後一個公理就是平行公理，簡寫為 Euclid‘s 5th Postulate (EFP)：一條直綫 $l$ 與其他兩條直綫 $m$ 和 $m’$ 相交，且這些線段在 $l$ 的同側所形成的內角之和小於180度，則線段 m 和 m’ 將會在該側的某一點相交。

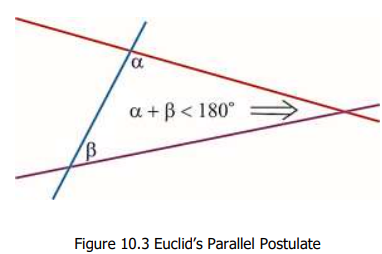
image-20230711141730219

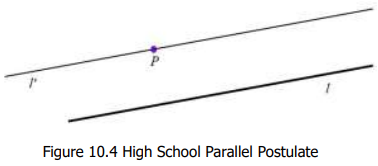
我們在高中學的是改良後的公理。

  • High School Parallel Postulate (HSP)：一條直綫 $l$ 與綫外一點 $P$，存在唯一的直綫 $l’$ 通過 $P$ 和 $l$ (平行) 不相交。

image-20230711141757767

乍看很直觀，但有幾個問題

  1. 什麼是直線？

    • 曲面上的直綫是 “geodesic”。有全域 (最短距離) 和局部 (acceleration vector 切向量為 0 或是基於 parallel transport ) 的定義

  2. 什麼是“永遠”不相交？還是相交在無限遠？數學家不喜歡沒有清楚的定義：永遠、極限、無限大/遠等等。

  3. HSP 只存在一條直綫和原來直綫平行不相交？可以有無限條 (平行) 直綫不相交，或是沒有任何 (平行) 直綫不相交？

非歐 (曲面) 幾何

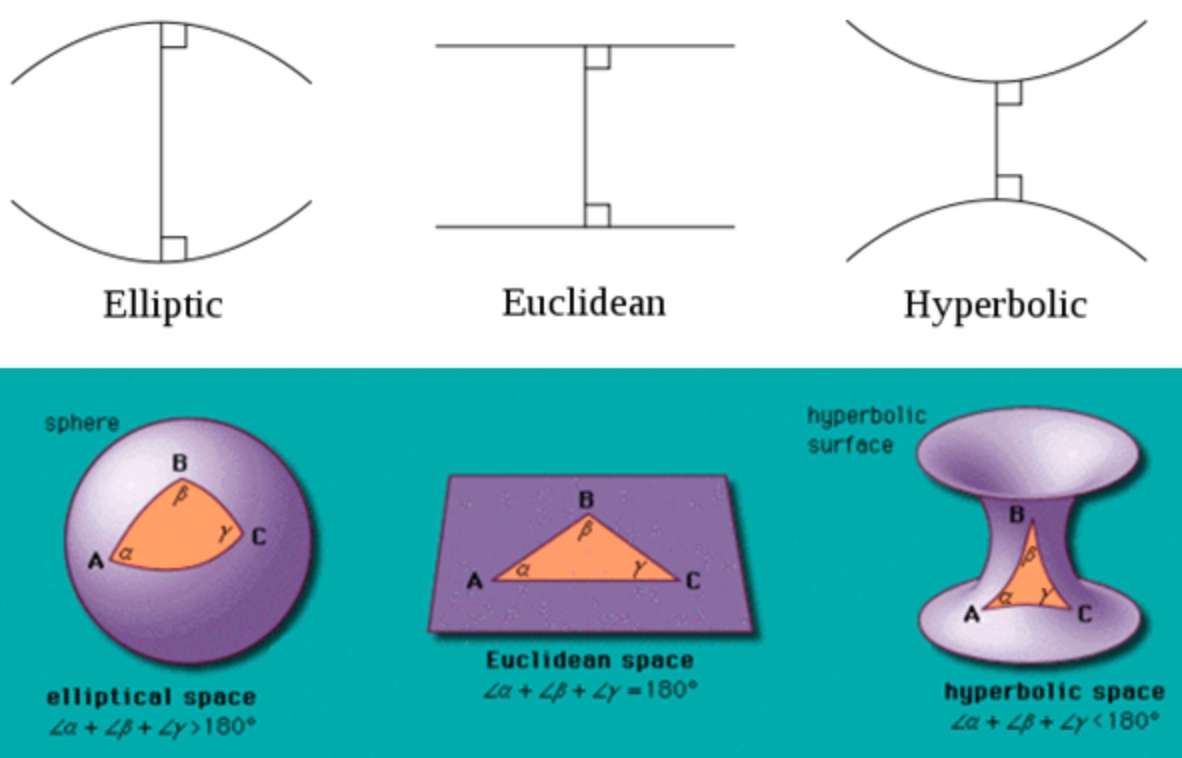
俄國數學家羅巴切夫斯基 (Lobachevsky) 一輩子想要其他公理證明平行公理或者用更直觀的公理取代平行公理都未能成功。後來用反證法：一條直線外一點一定會有兩條或兩條以上的 (平行) 直線和原來直綫不相交，試圖找出矛盾。但卻發現邏輯自洽。因而開創非歐幾何學。我們現在知道這其實對應雙曲面幾何如下。這是一個馬鞍面，立起來就是一個雙曲面。雙曲面上的”直線“線外一點可以找到無數 diverged “直線”，和原來的“直線”永不相交，因此可以有無數條平行線。

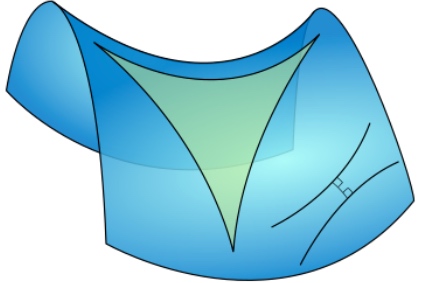
image-15690650751056

黎曼則另闢蹊徑開拓黎曼幾何學。對應（橢圓）球面幾何。球面上所有的“直線”都是 中心在球心的封閉大圓。因此所有的“直線”都相交。平行公理變成一條直線外一點沒有任何平行直線。常見的誤區是球面的緯線是平行線。緯線除了赤道是“直線”，其他的緯線都是球面上的“曲線”，不能視為平行直線！

下圖很好的總結三種幾何學。

image-15690766780502

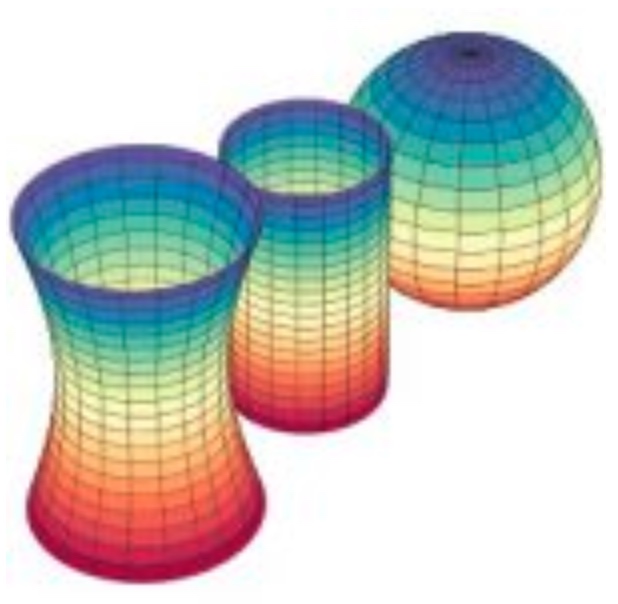
image-15690812862834

曲面幾何和曲率

非歐幾何的關鍵差異是曲率。曲面幾何可以定義沒一點的曲率。曲率乍看之下是把一個曲面放在更高維空間外視 (extrinsic) 的性質。

例如上圖是把二維的曲面放在（嵌入）三維的歐氏空間，可以明顯看出不同的曲面。同時可以定量的描述這個曲面的曲率。例如球面的曲率非常直觀和球的半徑相反。越小的球，曲率越大。但球面曲率是一個整體的性質，還是每一點（和其鄰近點）的性質？曲率是和半徑成反比，還是和半徑平方成反比？

先回顧二維歐氏平面上的一維曲線。很明顯曲線上每一點（和其鄰近點）都可以定義“線曲率” $\kappa$ 是相切圓（不是拋物線!）半徑的倒數，i.e. $\kappa = 1/r$. 當然可以根據相切圓是在曲線的上方或是下方定義 $\kappa$ 是正或是負。$\kappa$ 明顯和泰勒展開的二階導數成正比1。直線的二階導數為 0, 曲率為 0.

image-15696871816594

再回到二維曲面，曲面上每一點都有無限條曲面上的曲線相交於這一點。每一條曲線都有本身的“線曲率”，可以是正或負。高斯曲率定義二維曲面每一點的“曲面曲率” $R$ 是相交該點所有曲線（更正確應該是 geodesics）最大的線曲率乘最小的線曲率（含正負號）, i.e. $R = \kappa_1 \kappa_2$; $\kappa_1$ 是最大線曲率；$\kappa_2$ 是最小線曲率。

以完美球面為例，每一點所有相交曲線的線曲率都一樣。都是大圓（圓心即是球心）半徑的倒數。所以球面每一點的高斯曲率 $R = \kappa_1 \kappa_2 = 1/r^2$. 這符合直覺。

如果是非完美球面，例如橢圓球面半徑為 $(a, b, c)$, 曲面每一點的高斯曲

率都不同，還是可以找到對應的 $\kappa_1 \,, \kappa_2$. （完美或非完美）球面上同一點 $\kappa_1 \,, \kappa_2$一定同正或同負，所以橢圓幾何每一點的高斯曲率為正！

再考慮雙曲幾何。每一點相交曲線的”線曲率“必定有正有負，$\kappa_1 > 0 \,, \kappa_2 < 0$. 所以雙曲幾何每一點的高斯曲率為負！

外視和内視曲率

檢查高斯曲率在平面和圓柱面的曲率。平面是 trivial case, 所有 $\kappa=0$. 圓柱面就很有意思，x,y 軸切面是圓形，半徑為 d; z 軸切面是（兩條）直線。帶入高斯曲率，$\kappa_1 = 1/d \,,\, \kappa_2=0$, $R = \kappa_1 \kappa_2 = 0$. 也就是圓柱面每一點的高斯曲率為 0, 和平面一模一樣！

顯然這不直觀。直觀上會認為圓柱面和平面不同，具有曲率，至少在 x,y 方向有曲率。為什麼高斯會定義高斯曲率為 $\kappa_1 \kappa_2$ 而非 $(\kappa_1 + \kappa_2)/2$? (事實上，每一點的平均曲率定義為 mean curvature = $(\kappa_1 + \kappa_2)/2$）。

圓柱面是一個很好的例子，說明外視曲率和内視曲率的不同。

  • 外視曲率（extrinsic curvature）就是把曲面放在更高維的歐氏空間，從更高維歐氏空間測量和定義的曲率。

  • 内視曲率（intrinsic curvature）就是在（比嵌入歐氏空間低維）曲面本身測量和定義的曲率。更接地氣的說法，就是在曲面上的生物，可以測量和定義的曲率。

  • 舉例而言，上圖二維歐氏空間上的一維曲線，對於生活在曲線上一隻只會前進和後退（無限小）的蚯蚓，它能測量每一段曲線的長度，但是否能測量曲線上每一點的（内視）曲率？直觀上顯然不能。唯一的機會是封閉曲線。如果蚯蚓往一個方向前進，最後回到同一點，代表這是一條曲線。假設曲線是圓形，甚至可以算出整條曲線的平均直徑，以及整條線平均曲率。實務上沒有用途：（1）大多數的曲線都是開放而非封閉曲線。（2）即使是封閉曲線，很少是圓形，算出平均半徑，或是平均曲率沒有意義。注意曲率是每一點局部的特性。除非是完美圓形或球形，一條曲線的平均曲率沒有太大意義。上文的 mean curvature 是每一點相交曲線的平均曲率，是有意義。

  • 簡單而言，一維曲線的“線曲率” $\kappa$ 是嵌入在二維或是更高維歐氏空間，所以“線曲率”是外視曲率。

  • 再看二維曲面，上文由“線曲率”所定義的高斯曲率 $R = \kappa_1\kappa_2$ 或是 mean curvature = $(\kappa_1+\kappa_2)/2$ 應該也是外視曲率。NO!

  • 結果很意外。高斯曲率是内視 (bugs-eye-view) 曲率，mean curvature 是外視 (birds-eye-view) 曲率。

  • 對於二維曲面上的一隻螞蟻，不用線曲率，它能測量每一點的曲率嗎？能！見下文。具體的方法是在每一點畫一個圓（或三角形），測量圓的面積和 $\pi r^2$ 的差異並正規化，或是測量三角形內角和和 180 的角度差並正規化，就可以得到該點的高斯曲率 $R$。結果剛好等於最大和最小線曲率的乘積 $R = \kappa_1\kappa_2$.

  • 高斯自己似乎也覺得不可思議，稱為”絕妙定理“[@wikiTheoremaEgregium2019] 如下。

    “Gaussian curvature can be determined entirely by measuring angles, distances and their rates on a surface, without reference to the particular manner in which the surface is embedded in the ambient 3-dimensional Euclidean space. In other words, the Gaussian curvature of a surface does not change if one bends the surface without stretching it. Thus the Gaussian curvature is an intrinsic invariant of a surface.”

  • 所以平面和圓柱面的高斯曲率是相同的。一隻曲面上的螞蟻無法分辨局部是一個平面或是圓柱面。因為圓柱面展開是一個平面。但是 mean curvature 兩者不同。因為 mean curvature 是外視曲率。

  • 兩個曲面如果每一點高斯曲率相同，則為 isometric. 反之，無法 global isometric, 最多是 local isometric. 球面和平面無法等距 mapping. 只要看地圖就知道。赤道部分比例可以很準，但是兩極比例差很大。

  • 三維空間如何定義“内視“曲率？因為很難直觀想像三維彎曲空間嵌入一個四維空間。三維彎曲空間包含三個 basis (x, y, z), 每一點（和鄰近點形成的空間）可以分解成 xy, yz, xz 三組曲面，各自有高斯曲率。所以曲率是一個三維張量。Feymann lecture said there are 6 values to fully describe curvature.

  • 圓周率不是很好的曲面特徵，因為不是定值。Use N-dimension unit volume instead. S(r) = dV(r)/dr or dV(r) = S(r) dr (Gray and Vanhecke 1979).

  • 更重要的特徵是平行移動 (parallel transport) 以及沿著 close loop 的 parallel transport 的角度差，稱爲 holonomy. 平面幾何對於任何 close loop 的 H=0. 黎曼幾何 H > 0. 羅氏幾何 H < 0. Holonomy 是局部和全域連結的關鍵。

曲面幾何的其他特徵

除了平行公理可以用來分類不同的曲面，是否有其他更直觀的特徵分類？ Yes! 可以用三角形內角和是否大於，等於，或小於 $180^o \,(or \,\pi)$ 如下圖。

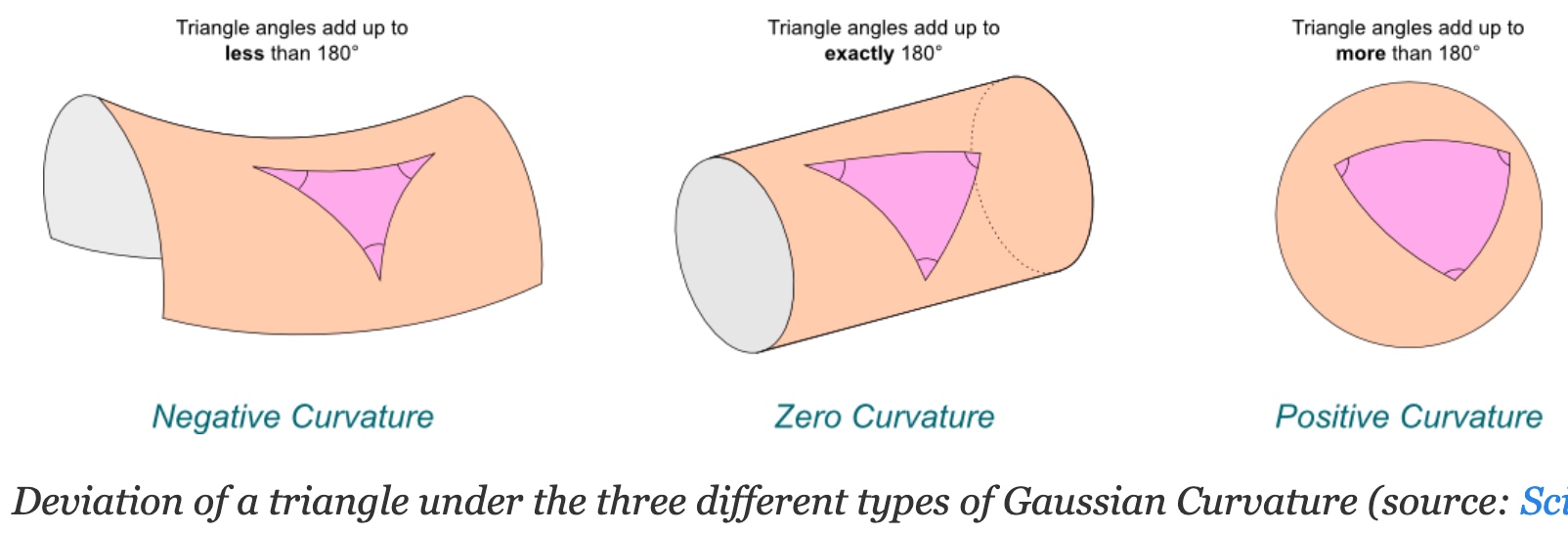
image-15690812589836

另外一個特徵是圓周率。在平面幾何任意圓的周長除以直徑永遠等於$\pi$. 但在曲面則會小於或大於$\pi$.
以上特徵（三角形內角和，圓周率）不只是定性的描述，都和高斯曲率有定量的關係。更重要的是這是曲面内視的特性！就是在曲面的生物，就可以測量到高斯曲率。

下表總結三種幾何學：

Creator 黎曼幾何 歐氏幾何 羅氏幾何
(Global) 曲面形狀 橢圓 平面/柱面 雙曲面
(Global) 高中平行公理：直綫外一點有幾條直綫不相交 0 1 $\ge 2$
(Global) 三角內角和 A > 180 A = 180 A < 180
(Global) 圓周率 $<\pi$ $\pi$ $>\pi$
(Global/local) Holonomy: PT 沿著 close loop 的角度差 H > 0 H = 0 H < 0
(Global/local) Independence of PT (!PT): PT 在任兩點相同和軌跡無關 No Yes No
(Local) 高斯曲率純量: K K > 0 K = 0 K < 0
(Local) 黎曼曲率張量: $R^a_{bcd}$ $R \ne 0$ $R = 0$ $R \ne 0$
(Local) Ricci 曲率張量: $R_{\mu\nu}$ $R \ne 0$ $R = 0$ $R \ne 0$

Q：上表的平行線，三角內角和，圓周率都是 global (全域) 特性。但是高斯曲率卻是 local (局部) 特性。如何連結 global and local？

A：Parallel transport。也就是 !PT 和 H=0

  • 圓周率 Bertrand–Diguet–Puiseux theorem (Wifi 2019a). 是否有積分形式？ \(K = \lim_{r\to0^+} 3 \frac{2\pi r - C(r)}{\pi r^3} = \lim_{r\to0^+} 12 \frac{\pi r^2 - A(r)}{\pi r^4}\)

  • 三角形內角和 (Gauss-Bonnet theorem （Wiki 2019a) \(\sum_{i=1}^3 \theta_i = \pi + \iint K dA \quad\text{or}\quad K = \lim_{A\to0^+}\frac{\sum^3 \theta_i - \pi}{A}\)

  • A good article to integrate everything including Laplacian using unit volume (Gray and Vanhecke 1979).

  • 一個明顯的問題是平行公理是全域的特性（直線永不相交），是否有直接對應局部公式？ Yes，平行移動 parallel transport 就是平行的微分定義!! 和曲面微分幾何有非常深層的連結。
  • 反向問題：既然可以用三角內角和以及圓周率極限定義曲率，還需要用平行定義取率嗎？ Absolutely Yes, 平行觀念和座標 grid line and local basis vector 定義吻合（local basis vector = grid line 的切線），可以直接融入純量場，向量場，張量場的微分運算。 相反三角內角和或圓周率基於極限的定義在各種微分幾何的運算並不實際。

(Keng 2018) 剛好和我想的一致，平行公理和 parallel transport.

Reference

  1. $\kappa = \frac{y’’}{(1+y’^2)^{3/2}}$ ↩ ↩2