Gauss-Bonnet Theorem

Posted on | In

Reference

Visual Differential Geometry and Forms: Tristan Needham! Excellent Book

Nanavaty.pdf (uchicago.edu) Interesting paper to derive GB 定理 from Stokes theorem

Takeaways

image-20240706210830528

Global Gauss-Bonnet Theorem 是一個例子。

Introduction

“Total change on outside = Sum of little changes on inside” 的想法，可以應用在任何可以内部互相抵消的應用。Gauss-Bonnet Theorem 就是一個例子。整理重點

  • “這個特性”是 additive: 例如梯度，旋度，散度

  • “這個特性”是可以互相抵消！

在微積分基本定理的 “這個特性” 就是微分，例如導數，梯度，旋度，散度。

在 Gauss-Bonnet Theorem，這個特性就是“高斯 (面) 曲率”!

彎曲空間的基本定理 Global Gauss-Bonnet Theorem (GBB)

假設 𝑀 是一個二維黎曼流形，∂𝑀 是其邊界。令 𝐾 為 𝑀 的高斯面曲率，$\kappa_g$ 為 ∂𝑀 的測地曲率 (geodesic curvature)。 𝜒(𝑀) 是 𝑀 的歐拉示性數 （Euler Characteristic）。則有

\[\int_M K d A+\int_{\partial M} \kappa_g d s=2 \pi \chi(M)\]

如果沒有邊界 (boundary)，例如球面 \(\int_M K d A=2 \pi \chi(M)\)

歐拉示性數： $\chi(M) = V - E +F$ 是拓撲不變量

Vertices, Edges, Faces.

  • 所有的 3D 凸立體：$\chi(M) = V-E+F = 2$， 包含立方體，金字塔，三角錐，球體，… 例如立方體：8 - 12 + 6 = 2.
    • 球：0 - 0 + 1 = 1 (wrong!). 定義為 2? 從赤道切成兩個半球。 1 - 1 + 2 = 2。另一個方法是用凸多邊體趨近一個球。
    • 所以凸多邊體包含球的拓撲特徵為 2.
  • 所有 2D 平面/曲面多邊形：$\chi(M) = V-E+F = 1$，包含三角形，長方形，圓形，… 例如正方形：4 - 4 + 1 = 1. 三角形 : 3 - 3 + 1 = 1. 圓形從任一點分開，包含一個 V, 一個 E, 一個 F：1-1+1 =1.

  • 如果有 k 虧格 $\chi-k$ 就是新的式性數。例如甜甜圈的 $\chi = 2-2 =0$，一個圓環則是 $\chi = 1-1 =0$

  • 這個定理非常美妙，把局部的幾何特性 (Gauss curvature, geodesic curvature) 和全域拓撲不變量 (歐拉示性數) 聯係起來。

比起高斯另一個著名的微分幾何的“絕妙定理” (Theorema Egregium) : 高斯曲率是曲面的内蘊特性，在局部的等距變換的不變量。更勝一籌。其實高斯或是博内 (Bonnet) 從來沒有寫下 (1) 的定理。甚至他們應該不知道歐拉式性數。但是高斯先後給了三個絕妙定理的證明。所以有時候也把”絕妙定理”稱爲 “Local Gauss-Bonnet Theorem” 有別於 Global Gauss-Bonnet Theorem，或是 GBB.

GBB 的拓展陳氏定理，或是 Chern-Gauss-Bonnet Theorem

陳省身把 GGB 推廣成高維形式：(非常重要的推廣，不過是無 boundary case) \(\chi(M)=\int_M e(\Omega)\) where $\chi(M)$ denotes the Euler characteristic of $M$. 注意此處 $M$ 是 2n 黎曼流形沒有邊界。所以沒有 $\partial M$ 的積分。n =1 化簡成 Gauss-Bonnet Theorem without boundary. \(e(\Omega)=\frac{1}{(2 \pi)^n} \operatorname{Pf}(\Omega) \text {. }\)

  • $n = 1$， 2D 對應 GGB 定理無 boundary case：$K$ 是高斯（面）曲率

    \[2 \pi \chi(M)=\int_M K dA\]

  • $n = 2$，4D 對應愛因斯坦的相對論：$K$​ 是高斯（面）曲率

    • Riem 是黎曼曲率，Ric 是 Ricci 曲率，R 是純量曲率
    \[32 \pi^2 \chi(M)=\int_M \vert Riem \vert^2 - 4 \vert Ric \vert^2 + R^2 d\mu\]

解讀 GGB 定理 (Global Gauss-Bonnet Theorem)

我們如何解讀 GBB 這個定理，他的幾何直觀在哪裏？

  • $K$ 是面曲率 of $M$，$\kappa_g$ 是綫曲率 of $\partial M$。兩者完全不是微分的關係。和選取的邊界 ($\partial M$) 有直接的關係。後面用球蓋的例子説明。

  • 有兩個角度解讀 GB 定理：

    1. 球形曲面高斯曲率 = $1/R^2$ 的推廣 ($\chi=2)$。以及圓形的綫曲率 = $1/r$ 的推廣 ($\chi=1$​)。
    2. 高斯曲率 = (三角形内角和 - $\pi$)/(面積) 的推廣

  • 基本上 $K = \kappa_1 \kappa_2$。$K$ 和 $\kappa_g$ 并不是直接微分的關係，但是 “total change on outside = sum of little changes on inside”。之後好好推導一下！

我們深入探討一下 $K$ 和 $\kappa_g$ 的關係。

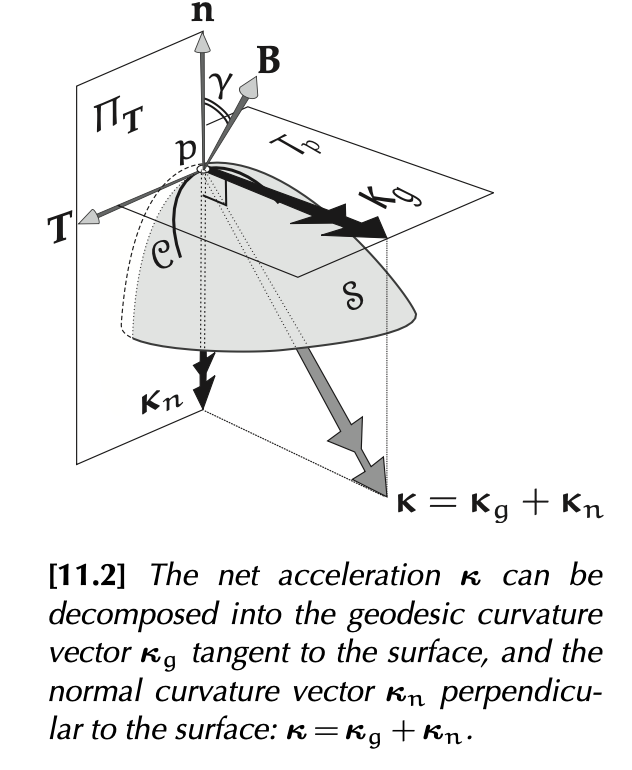
  1. M 的任何曲線的曲率向量 $\boldsymbol{\kappa}$可以分解成 $\boldsymbol{\kappa}_g$ (geodesic curvature) and $\boldsymbol{\kappa}_n$ (normal curvature)

    向量 $\boldsymbol{\kappa} = \boldsymbol{\kappa}_g + \boldsymbol{\kappa}_n = \kappa \boldsymbol{N} = \frac{d\boldsymbol{T}}{ds}$ ， 純量$\kappa^2 = \kappa_g^2 + \kappa_n^2$ . 這裏的 $\boldsymbol{N}$ 是 C 在 p 點附近加速度（向心力）的方向。和切平面 $T_p$ 的曲率分量 $\boldsymbol{\kappa}_g$ 方向有一個夾角 $\gamma$. 同樣 $\gamma$ 也是切平面的法向量 $\boldsymbol{n}$ 和 Frenet frame 的 $\boldsymbol{B}$ 的夾角如下圖。

    $\kappa_g = \kappa \cos\gamma$ and $\kappa_n = \kappa \sin \gamma$

image-20240710220648371

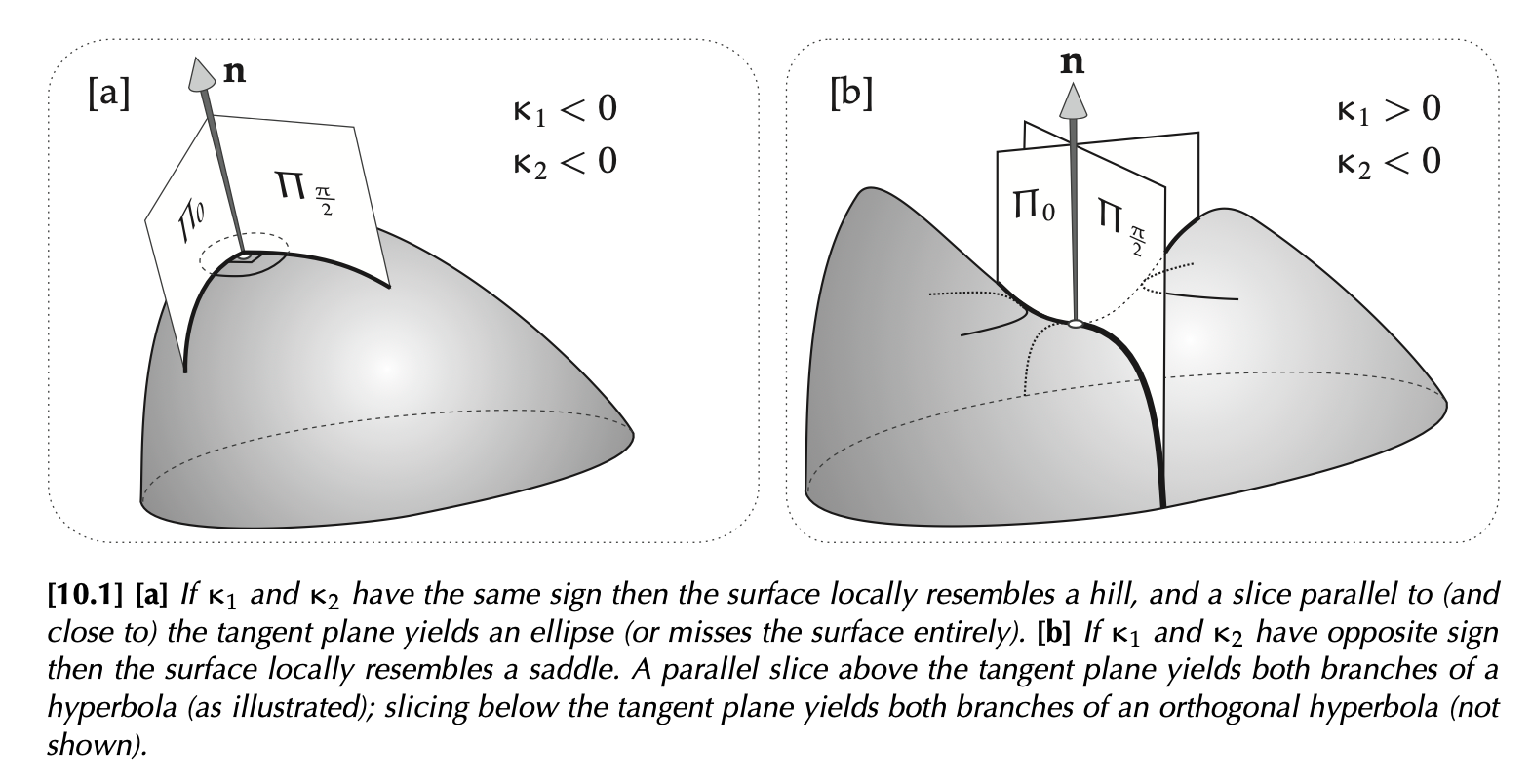
$\kappa_n$ (Normal direction) 再分解成 $\kappa_1$ and $\kappa_2$. $\theta$ 是這條線在 p 點和 principal direction 的角度，$\gamma$ 則是這條線在 p 點形成的面的 normal 和 M 的面的 normal 的夾角。

$\kappa_n(\theta) = \kappa_1 \cos^2(\theta) + \kappa_2 \sin^2(\theta)$

而高斯面曲率則是 $K = \kappa_1 \kappa_2$​

所有 K 和 $k_g$ 的關係 depends on $\theta$ 和 $\gamma$

image-20240710221516763

球形和圓形，解讀和驗證 GGB （直觀而且重要）

1. 半徑為 R 的曲面球 ($K=\frac{1}{R^2}, \chi =2$ )，沒有 boundary

\[\int_M K d A = 4 \pi R^2 \frac{1}{R^2} = 4 \pi = 2 \pi \chi(M)\]

這是一個 trivial case, 但也是 GGB 的基本盤。

2. 半徑為 r 的平面圓 ($K=0, \kappa_g = \frac{1}{r}, \chi =1$ )

\[\int_M K d A+\int_{\partial M} \kappa_g d s= 2\pi r \frac{1}{r} = 2\pi = 2 \pi \chi(M)\]

這也是一個 trivial case。

3. 半徑為 R 的半球 ($K=\frac{1}{R^2}, \kappa_g = 0, \chi =1$ )，半球和圓的拓撲同構 (homomorphism)

半球的邊界 $\partial{M}$ 是大圓，因此 $\kappa_g = 0$ \(\int_M K d A+\int_{\partial M} \kappa_g d s= 2\pi R^2 \frac{1}{R^2} + 2 \pi R \cdot 0 = 2\pi = 2 \pi \chi(M)\)

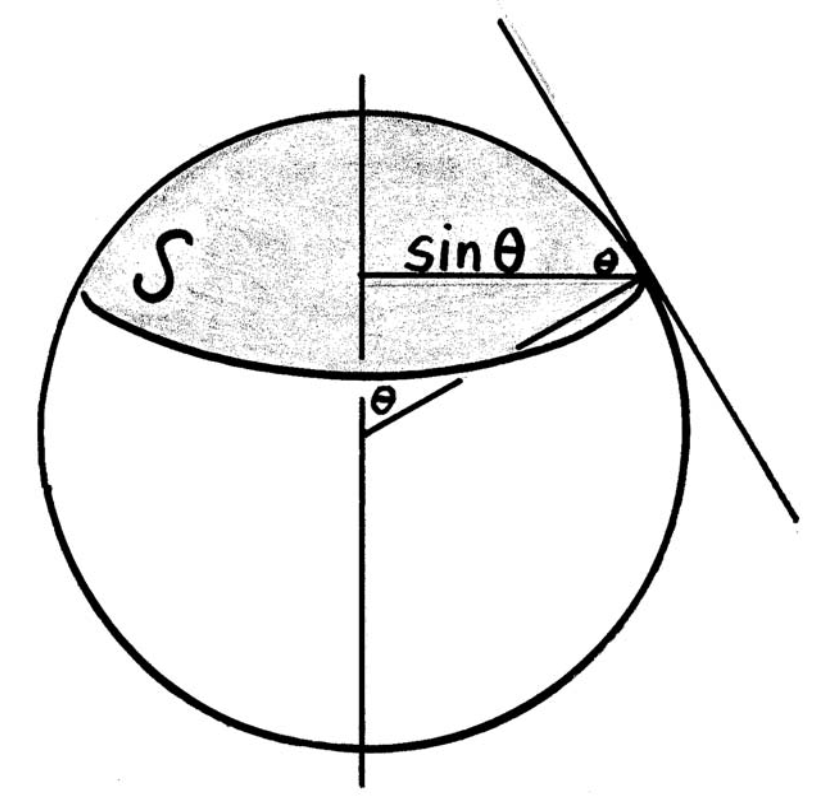
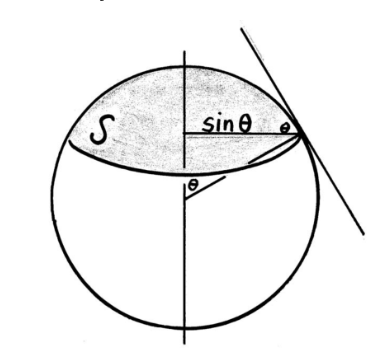
4. 半徑為 R 的球蓋 ($K=\frac{1}{R^2}, \kappa_g = \frac{1}{R \tan \theta}, \chi =1$ )，球蓋和圓的拓撲同構 (homomorphism)

如下圖，polar cap 。 $\gamma$ 或是 $\theta$ 是向心力方向和切平面 $T_p$ 的夾角。

image-20240711211635546

  • Area $S=\int_0^{\theta} 2 \pi R \sin \theta \, R \mathrm{d} \theta=2 \pi R^2 (1-\cos \theta)$ 所以 GBB 的第一項： $\quad \int_{\mathrm{S}} K dS =1 \times\mathrm{S}=2 \pi(1-\cos \theta)$. $\theta=\pi/2$ 對應半球，此項為 $2\pi$ 和上面半球的結果相符。

  • The curvature $\kappa$ of $\partial \mathrm{S}$ $\kappa = 1/\text{ radius } = 1/(R \sin\theta)$

    The geodesic curvature $\kappa_{\mathrm{g}}$ of $\partial \mathrm{S}$ is $\kappa \cos \gamma = \kappa \cos \theta = \cos\theta/(R \sin\theta) = 1/ (R \tan \theta)$, 所以 GBB 的第二項：

\[\begin{aligned} \int_{\partial \mathrm{S}} \kappa_{\mathrm{g}} \mathrm{ds} & =\kappa_{\mathrm{g}} \times \text { length }(\partial \mathrm{S}) \\ & =(\cos \theta / R \sin \theta) 2 \pi R \sin \theta=2 \pi \cos \theta . \end{aligned}\]

​ 同樣 $\theta=\pi/2$​ 對應半球，此項為 0 和上面半球的結果相符。

  • 完整的 GBB 如下：
\[\begin{aligned} \int_{\mathrm{S}} K dS+\int_{\partial \mathrm{S}} \kappa_{\mathrm{g}} \mathrm{ds} & =2 \pi(1-\cos \theta)+2 \pi \cos \theta \\ & =2 \pi=2 \pi \chi(\mathrm{S}) . \end{aligned}\]

5. 半徑為 R 的球蓋，$\theta = \epsilon\to 0$ ($K=\frac{1}{R^2}, \kappa_g = \frac{1}{R \epsilon}, \chi =1$ )，球蓋和圓的拓撲同構 (homomorphism)

$\gamma=\theta = \epsilon \to 0$,

  • GBB 第一項 $2\pi(1-\cos\theta) = \pi \epsilon^2$. 基本是北極附近的小圓盤，面積是 $\pi (R \epsilon)^2 = \pi \epsilon^2 R^2$。但面曲率不爲 0，而是 $1/R^2$​.

    • 所以 GBB 第一項：$\pi\epsilon^2$

  • GBB 第二項 $2\pi \cos\theta = 2\pi(1-\epsilon^2/2)$. 雖然 $\kappa_g = 1/(R\epsilon)\to \infty$，但是周長約為 $2\pi R\epsilon$。但因爲面曲率不爲 0，周長修正為 $2\pi R \epsilon (1-\epsilon^2/2)$.

    • 所以 GBB 第二項：$2\pi(1-\epsilon^2/2)$
    • 用圓形周長 excess (1st-order): $2\pi R\epsilon - (2\pi R \epsilon (1-\epsilon^2/2)) = \pi R \epsilon^3$ , 周長 excess / $r^3 \cdot 3/\pi = \pi R \epsilon^3 / (R\epsilon)^3 \cdot 3/\pi= 3/R^2$ ? 差了 3 倍。

    image-20240330101851574

曲面三角形，解讀和驗證 GGB 可以用於任何曲面

Total change outside = Sum of little changes inside

從球面三角形定義高斯曲率 K：

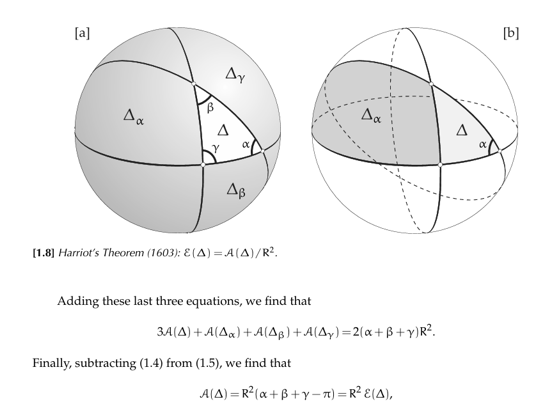
image-20240707233504364

  • $K = \mathcal{E}(\Delta) / A(\Delta) = 1/R^2$ 就是 angular excess / area. 所以對於球面三角形，三個邊是大圓，也就是 geodesics 三角形：
    • $\int_{\Delta} K d A = \mathcal{E}(\Delta) = \alpha + \beta + \gamma - \pi $​
  • GBB 的第一項：我們後面會證明，對於任意曲面，$\int_{\Delta} K d A = \alpha + \beta + \gamma - \pi$, 只要三個邊是 geodescis.

GBB 的第二項：$\int_{\partial\Delta} \kappa_g d s = 3 \pi - \alpha - \beta - \gamma$​

所以 GBB 如下。高斯曲率產生 angular excess 對應的第一項，被第二項抵消三角形内角而剩下 $2\pi$. \(\int_{\Delta} K d A+\int_{\partial \Delta} \kappa_g d s= 2\pi = 2 \pi \chi(M)\) 以上 geodesic 三角形的 angular excess per unit area 定義，和 parallel transport 經過一個 close loop (A -> B -> C -> A) 得到：（K = 角度差/面積） 的定義完全等價！

  • Geodesic 三角形的 angular excess per unit area 在現實上比 parallel transport 容易操作。

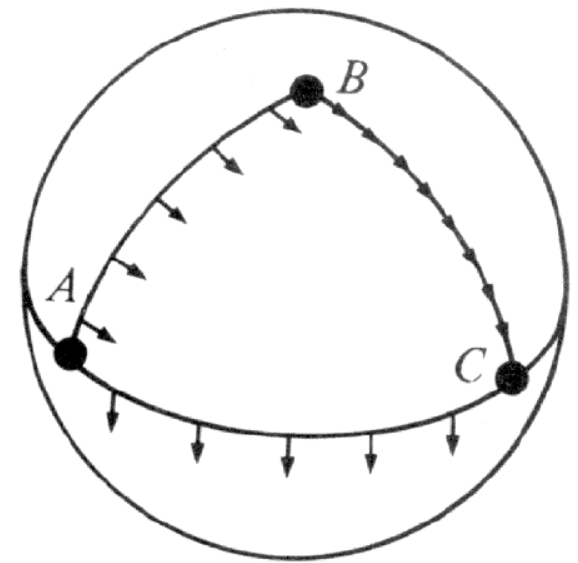
image-20240707233939367

如何證明兩者等價？看下圖的 close loop (P -> A -> B -> P) :

  • P -> A: parallel transport
  • 在 A 點：角度轉了 $\pi - \alpha$
  • A -> B: parallel transport
  • 在 B 點：角度轉了 $\pi - \beta$
  • B -> P: parallel transport
  • 在 P 點：角度轉了 $\pi - \gamma$​

比起 parallel transport，這三個昏頭轉向其實就是多了 $2 \pi$​ 的角度回轉。

因此我們把三次的角度加起來，再減掉 $2\pi$，就和 parallel transport 一樣

  • parallel transport P->A->B->P = $ \pi-\alpha+\pi -\beta + \pi - \gamma - 2 \pi = \pi - (\alpha+\beta+\gamma)$
  • 一般我們定義正負號 (順時針?) 所以 x (-1) : parallel transport = $ \alpha+\beta+\gamma - \pi$ . 因此兩者等價。

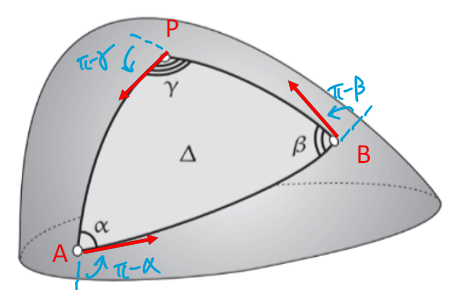
image-20240707232648879

再來應用 “total change on outside = sum of little changes on inside”

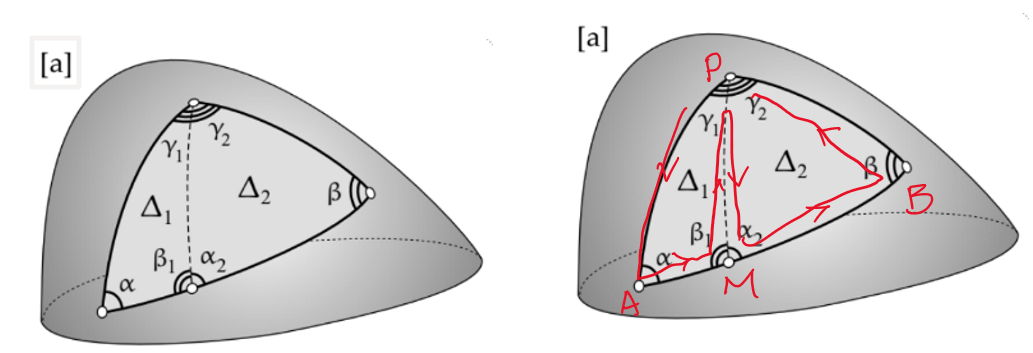
  • Additive: 把大的 geodesic 三角形從 M 點切成兩個小的三角形。 大的三角形 angular excess = 兩個小的三角形的 angular excess 之和
  • 抵消： 我們看下圖右比較清楚：從 parallel transport 的角度，多了 M 只是把 M->P 和 P->M 的 parallel transport 抵消。
  • 如果是從 angular excess 的角度，就是 $\beta_1 + \alpha_2 = \pi$： $ \alpha+\beta_1+\gamma_1 - \pi + \alpha_2+\beta+\gamma_2 - \pi = \alpha + \beta + \gamma_1+\gamma_2-\pi = \alpha+\beta+\gamma-\pi$

image-20240708001239020

最後 no surprise

1. 曲面三角形的 $\chi = 1$ \(\int_M K d A+\int_{\partial M} k_g d s= \int_M K d A+ (\pi - \alpha+\pi-\beta+\pi-\gamma) = 2 \pi \\ \int_M K d A = \alpha+\beta+\gamma - \pi\) image-20240708002203297

如果是平面三角形： K = 0, $\alpha+\beta+\gamma = \pi$

GBB 在有洞 (hole) 的曲面

環型

基本可以用 polar cap 再切一次。

image-20240714234119645

image-20240714234249199 \(\int_S K d A+\int_{\partial S} k_g d s= 2 \pi \\ \int_{S'} K d A +\int_{\partial S'} k_g d s= 2 \pi \\ \int_{S-S'} K d A +\int_{\partial S - \partial S'} k_g d s= 2 \pi \chi(S-S')\) 也就是 $S-S’$ 的歐拉式性數為 0. 我們可以推理如果有 $k$ 個洞，歐拉式性數 $\chi = 1 - k$.

另一個方法是用三角形 (TBD) 挖洞？還是連起來。TBD

GBB 在有刺 (Spike) 曲面 = Polar Cap

也是利用 GGB 定義刺的曲率。

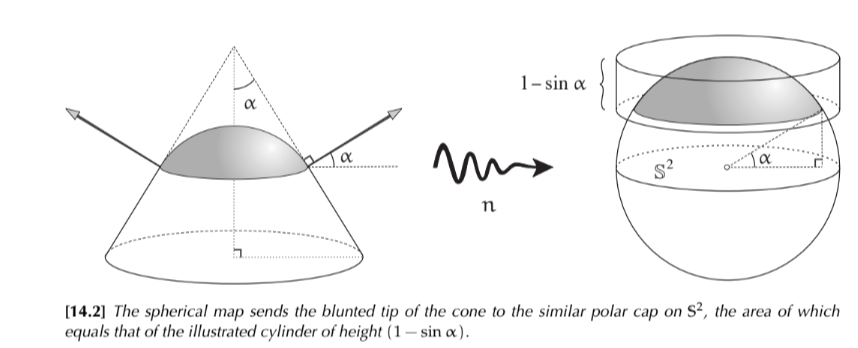
image-20240715001239034

image-20240715001303682

image-20240715001320694

GBB 的第一項除了 spike tip 之外都是 0, 但是可以用上面的方法得到。

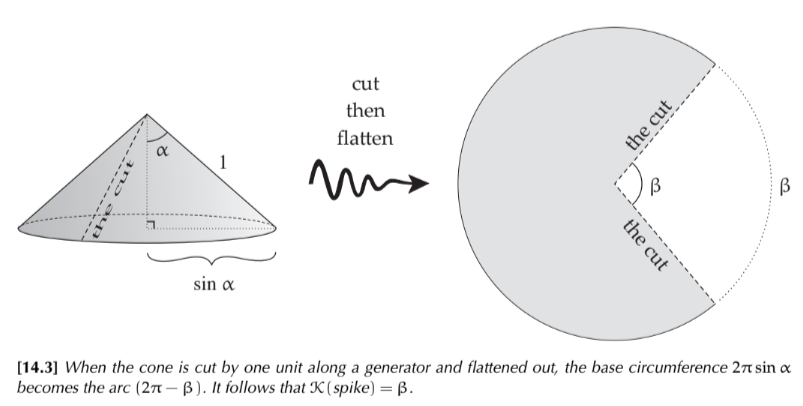
image-20240715001432627

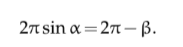
image-20240715002101177

$\alpha = \pi/2 - \gamma = \pi/2 - \theta$

GBB 的第一項：$2\pi (1-\sin\alpha) = 2 \pi (1 - \cos\theta)$

GBB 的第二項： \(\begin{aligned}\int_{\partial \mathrm{S}} \kappa_{\mathrm{g}} \mathrm{ds} & =\kappa_{\mathrm{g}} \times \text { length }(\partial \mathrm{S}) \\& =(\cos \theta / R \sin \theta) 2 \pi R \sin \theta=2 \pi \cos \theta .\end{aligned}\)

  • 完整的 GBB 如下：基本和 polar cap 一模一樣。
\[\begin{aligned} \int_{\mathrm{S}} K dS+\int_{\partial \mathrm{S}} \kappa_{\mathrm{g}} \mathrm{ds} & =2 \pi(1-\cos \theta)+2 \pi \cos \theta \\ & =2 \pi=2 \pi \chi(\mathrm{S}) . \end{aligned}\]

Appendix

Gauss 曲率和度規的關係

\[\begin{gathered} \mathrm{d} \hat{\mathrm{s}}^2=\mathrm{A}^2 \mathrm{~d} \mathrm{u}^2+\mathrm{B}^2 \mathrm{~d} v^2 . \\ K=-\frac{1}{\mathrm{AB}}\left(\partial_v\left[\frac{\partial_v \mathrm{~A}}{\mathrm{~B}}\right]+\partial_{\mathrm{u}}\left[\frac{\partial_{\mathrm{u}} \mathrm{B}}{\mathrm{A}}\right]\right) . \\ \mathrm{d} \hat{\mathrm{s}}^2=\Lambda^2\left[\mathrm{du}+\mathrm{d} v^2\right] . \\ \mathcal{K}=-\frac{\nabla^2 \ln \Lambda}{\Lambda^2} . \end{gathered}\]

Reference