Source
Tweet: “Quantum mechanics is just thermodynamics in imaginary time.”
Complex Analysis L06: Analytic Functions and Cauchy-Riemann Conditions (youtube.com)
Cauchy–Riemann equations - Wikipedia
Visual Differential Geometry and Forms: Tristan Needham! Excellent Book
Visual Complex Analysis: Needham
Baidu video 半径为i的圆!三维空间是什么形状 (baidu.com)
(數學太多) Tweet of Lorentz invariant [2402.14730] Clifford-Steerable Convolutional Neural Networks (arxiv.org)
Very good video about Minkowski space: (44) Relativity 104e: Special Relativity - Spacetime Interval and Minkowski Metric - YouTube
引言
量子力學只是虛時間中的熱力學。
這個簡潔的陳述概括了我們之前討論的複雜概念。它強調了量子力學和熱力學之間的深層聯繫,這種聯繫是通過時間變量的數學變換(實時間到虛時間)來實現的。這個觀點揭示了這兩個看似不同的物理領域之間存在的令人驚訝的數學和概念上的相似性。
雖然這個陳述捕捉到了一個深刻的見解,但它是一個簡化的表述。實際上,這兩個領域之間的關係更加複雜和微妙,涉及到更多的數學和物理細節。
乍聽之下,這可能聽起來像是一個模糊的、準哲學的陳述,但是稍微深入研究雙曲線和拋物線偏微分方程(PDEs)之間的關係,就會發現這可以在數學上被形式化。
Second Order PDE
二階偏微分方程根據其與時間和因果律的關係,大致可分為雙曲型、橢圓型或拋物型。
雙曲型偏微分方程(閔氏空間,偏時空)包含時間和因果關係的概念: 在域內的擾動以波浪狀方式以有限速度向外傳播。
橢圓型偏微分方程(歐氏空間,偏幾何)缺乏這種時間和因果關係的概念: 擾動立即影響整個域,信息傳播速度實際上是無限的。
拋物型偏微分方程處於一個奇特的中間位置 (偏擴散 diffusion): 它們承認時間的流逝,但缺乏因果關係的感覺。在這些偏微分方程中,擾動仍然立即影響整個域(類似於橢圓型偏微分方程),但隨時間擴散。
2nd Order PDE to Coupled 1st Order PDE
我們可以通過將二階偏微分方程簡化為一階偏微分方程的耦合系統來數學形式化這些特徵。決定二階偏微分方程中因果關係和信息流動 (i.e. 時間) 的特徵由描述一階偏微分方程耦合系統的 2x2 矩陣的特徵值 (eigenvalues) 給出。求解這個二次方程會得到 1. 兩個不同的實特徵值, 2. 沒有實特徵值(兩個不同的複特徵值),或者3. 一個重複/退化的實特徵值。
兩個實特徵值
當我們有兩個不同的實特徵值時,有兩條特徵線結合形成一個時空錐。這個錐體代表域中每個點的過去和未來”光錐”,表示具有有限信息傳播速度的雙曲型偏微分方程。
兩個複特徵值
在沒有實特徵值的情況下(即有兩個不同的複特徵值),沒有特徵線,表示具有無限快信息傳播速度的橢圓型偏微分方程。
單一/退化實特徵值
在單一/退化實特徵值的情況下,單一特徵線代表時空域中的垂直線。這代表拋物型偏微分方程,其域中的每個點都依賴於其過去的所有點 (沒有光錐/因果結構), 但不依賴於其未來的任何點。本質上,單一特徵線整齊地將過去與未來分開。
虛時間
通過將偏微分方程中的一個變量轉換為虛數,例如進行 ( $t \rightarrow it$ ) 轉換,我們可以改變二次判別式的符號。這種轉換可以將先前的拋物型偏微分方程轉換為雙曲型 (或橢圓型) 偏微分方程。
將這種 ( $t \rightarrow it$ ) 轉換應用於熱方程,一個代表熱力學中熱擴散的典型拋物型偏微分方程,通過強制先前單一退化的特徵值變為不同的複特徵值,產生了一個雙曲型偏微分方程。
值得注意的是,這種轉換產生了薛定諤方程,描述了量子力學中波函數的演化。這種轉換被稱為維克旋轉 (Wick rotation) ,它允許將量子力學問題轉換為熱力學問題,反之亦然。
量子力學和熱力學的相似度
這解釋了為什麼相似的概念, 如 correlation 函數和 partition 函數, 會同時出現在量子力學和統計力學中,儘管它們看似不同。它還解釋了為什麼薛定諤方程中的項 $\exp(-iHt)$ 在形式上類似於吉布斯測度中的 $\exp(-\beta H) $ 項;它們本質上是相同的項,通過 $t \rightarrow it$ 轉換相關。
這種對偶性通過奧斯特瓦爾德-施拉德定理延伸到量子場論,該定理嚴格地關聯了量子場論和統計場論。雖然關於這種形式類比還有很多需要理解的地方,但它突出了二階偏微分方程的一個基本特徵:實時間中的擴散與虛時間中的波傳播相關,反之亦然。
Diffusion Equation \(\frac{\partial \phi(\mathbf{r}, t)}{\partial t}=D \nabla^2 \phi(\mathbf{r}, t), \quad\)
Heat Equation,基本和 Diffusion Equation 一樣 \(\frac{\partial u(\mathbf{r}, t)}{\partial t}= k \nabla^2 u(\mathbf{r}, t)\)
Schrodinger Equation ($t \to it$) \(i \hbar \frac{\partial \Psi(\mathbf{r}, t)}{\partial t} =-\frac{\hbar^2}{2 m} \nabla^2 \Psi(\mathbf{r}, t)\)
Wave Equation \(\frac{\partial^2 u(\mathbf{r}, t)}{\partial t^2} =c^2 \nabla^2 u(\mathbf{r}, t)\)
幾何的角度
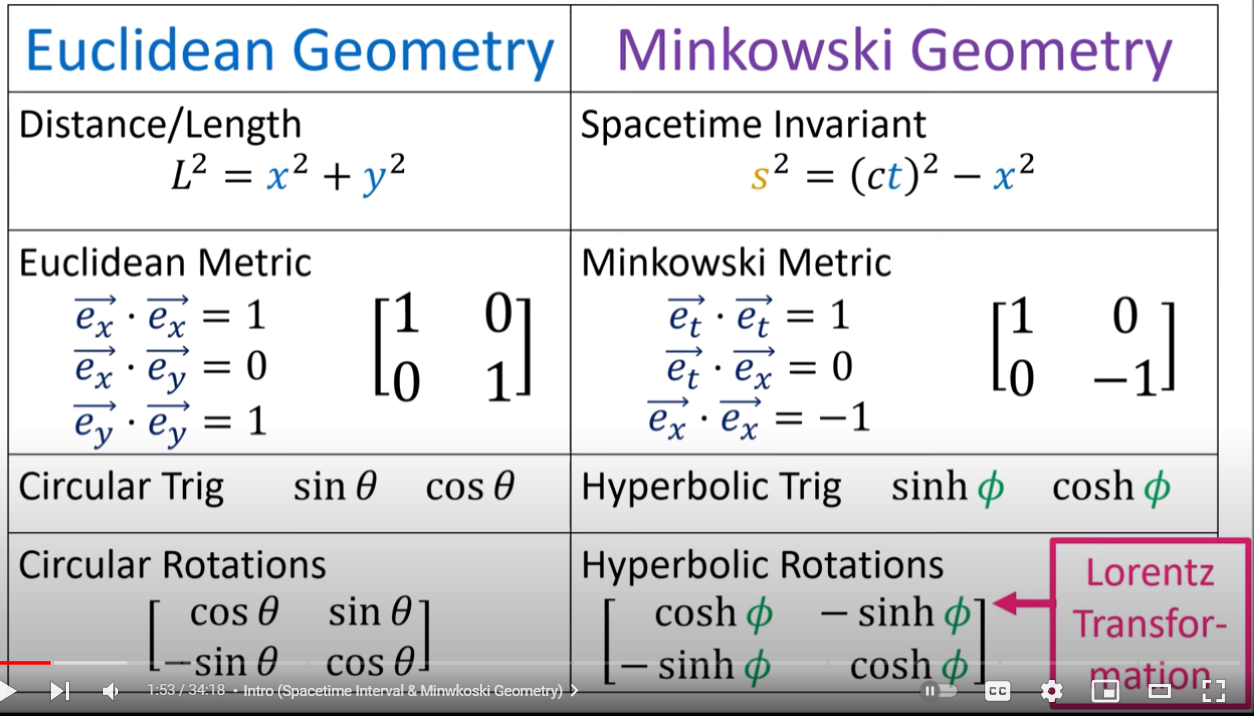
用歐氏幾何和閔氏幾何比較:
歐氏幾何是純粹幾何,沒有時間的觀念。或是所有事件都是同時發生。例如廣義相對論中重力質量和加速度質量一樣(等效原理)可以視為是一種類幾何性質。就是所有近地物體感受到的重力加速度都一樣。
閔氏幾何把其中一維變成虛軸 (時間),創造出光錐,所有的事件要在光錐中才互相作用,而且速度不能大於光速。
我們用一個幾何的例子來說明:
複平面圓形
普通半徑為 1 的圓在實平面或複平面都非常簡單: $f(z) = \mid z \mid ^ 2 = \mid a + b i \mid ^2 = a^2 + b^2 = 1^2$
我們更有興趣是半徑為 $i$ 的圓。顯然在實平面不存在。但是在複平面存在嗎,是什麽形狀?
複平面或是複空間:
$(x+ i y)^2 + (a + i b)^2 = r^2$
我們 4D 投影到 3D 才看得到。所以變成
$(x)^2 + (a + i b)^2 = r^2$
$r = 1$
$(x)^2 + (a + i b)^2 = 1^2 = 1$
$(x^2 + a^2 - b^2) + 2 a b i = 1$
if $a = 0 \to x^2 - b^2 = 1$ 這是雙曲綫
if $b = 0 \to x^2 + a^2 = 1$ 這是圓形
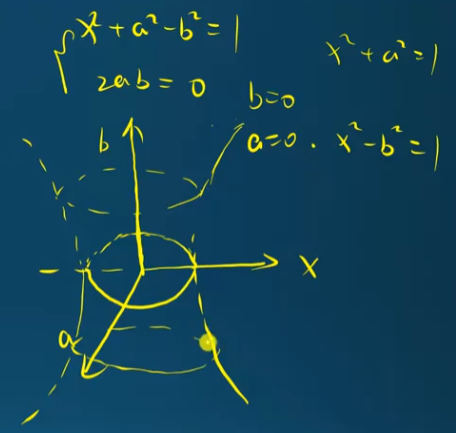
如下圖是雙曲圓柱形, How? 不是 $a, b$ 一定要有一個為 0?
記住這是 4D 到 3D 一個角度的投影!我們要想象 $y \ne 0$ 的情況,才會得到完整 4D 到 3D 的投影:雙曲圓柱形!
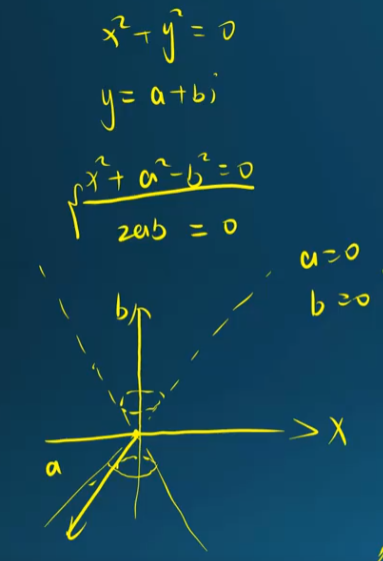
if $r = 0$
$(x)^2 + (a + i b)^2 = 0^2 = 0$
$(x^2 + a^2 - b^2) + 2 a b i = 0$
if $a = 0 \to x^2 - b^2 = 0$ 這是兩條綫
if $b = 0 \to x^2 + a^2 = 0$ 這是點
所以是完整 4D 投影到 3D 是圓錐形?
if $r = i$
$(x)^2 + (a + i b)^2 = r^2 = i^2 = -1$
$(x^2 + a^2 - b^2) + 2 a b i = -1$
if $a = 0 \to x^2 - b^2 = -1$ 這是雙曲綫
if $b=0$ 無解。所以是如下的雙曲面。可以視爲圓心在無窮遠的地方嗎?
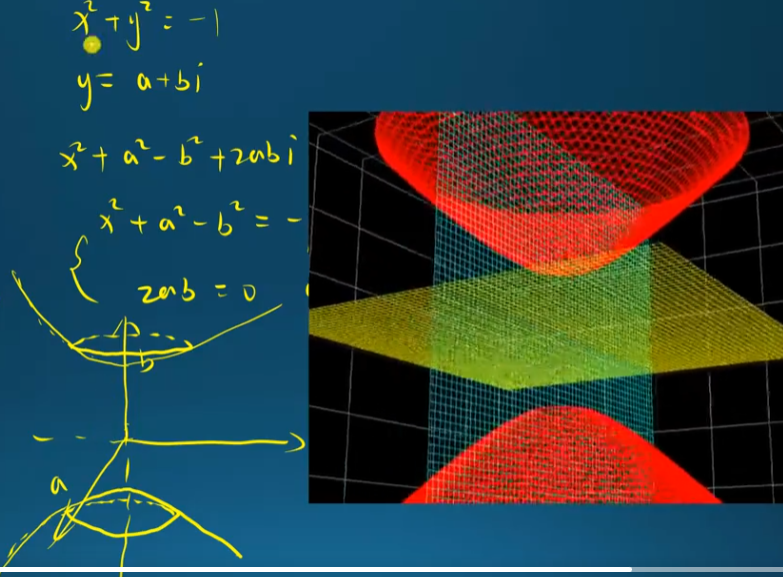
半徑為 $i$ 的圓有什麽意義?Minkowski 空間
Minkowski 空間可以看作是複半徑圓。就像單位圓是 Euclidean 空間的基本。
Euclidean 空間的物理定律,經過實單位圓的坐標轉換仍然不變,稱爲不變群 O(n).
最簡單的是 O(2), 坐標軸旋轉對於物理定律不變。
\[\begin{bmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta\\ \end{bmatrix}\]Lorentz Transformation and Invariance
Minkowski 空間的物理定律,經過複單位圓的坐標轉換仍然不變,也稱爲不變群, Lorentz group
\[\begin{bmatrix} \cosh t & \sinh t\\ \sinh t & \cosh t\\ \end{bmatrix}\]這個坐標轉換的不變性,也可以從微分幾何的第一式出發。注意 Minkowski 和 Euclidean 空間都是平直空間!
先定義 Minkowski 空間:Minkowski 空間是一個四維空間,將三維歐幾里得空間和時間結合成一個單一的流形。它用於狹義相對論理論中,具有平坦的幾何結構,其度量符號為 (-+++)。
Lorentz變換描述了兩個以恆定速度相對運動的觀察者之間事件座標的變化。它們確保了光速在所有慣性參照系中是恆定的。
在Minkowski 空間中,度量張量 $\eta_{\mu\nu}$ 定義了時空間隔:$ds^2 = -c^2dt^2 + dx^2 + dy^2 + dz^2$
其中 $ds$ 是不變間隔,$(t, x, y, z)$ 是座標。 Lorentz變換可以使用矩陣運算來表示Minkowski 空間中的四維向量。對於座標為 $x^\mu = (ct, x, y, z)$ 的事件,Lorentz變換 $\Lambda$ 的作用如下: $ x’^\mu = \Lambda^\mu_{\ \nu} x^\nu $ 其中 $\Lambda$ 是一個 4x4 的矩陣,滿足 $\Lambda^\mu_{\ \alpha} \Lambda^\nu_{\ \beta} \eta_{\mu\nu} = \eta_{\alpha\beta}$。 Lorentz不變性意味著時空間隔 $ds^2$ 在Lorentz變換下保持不變: $ds’^2 = \eta_{\mu\nu} x’^\mu x’^\nu = \eta_{\mu\nu} (\Lambda^\mu_{\ \alpha} x^\alpha)(\Lambda^\nu_{\ \beta} x^\beta) = \eta_{\alpha\beta} x^\alpha x^\beta = ds^2$ 這種不變性確保了物理定律對所有慣性觀察者都是一致的。
利用微分幾何,Minkowski 空間被描述為一個具有度量張量定義時空間隔的四維流形。Lorentz變換是保持此間隔不變的線性變換,確保了Lorentz不變性。
虛數圓的意義 ($r^2 =0$ 是光錐, $r^2 < 0$ 是光錐之内,兩個事件有因果關係,$r^2 > 0$ 是光錐之外,兩個事件無法觀察因爲超過光速 )
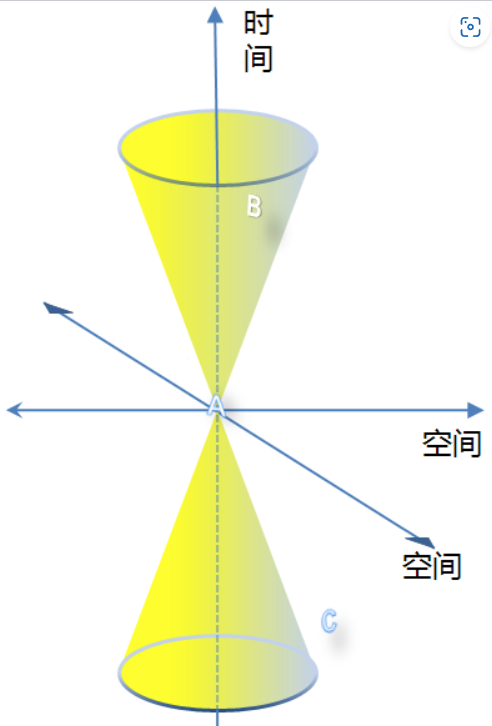
在Minkowski 空間中,兩個事件之間的時空間隔 $s^2$ 為: $s^2 = c^2(t_2 - t_1)^2 - (x_2 - x_1)^2 - (y_2 - y_1)^2 - (z_2 - z_1)^2$ 這個間隔可以是正的、負的或零,取決於事件在時間和空間中的相對分離。
在Minkowski 空間中,如果我們考慮一個“圓”(實際上是四維空間中的超球體),我們可能會遇到間隔為負的情況。例如,僅考慮兩個空間維度和時間:如上圖 $s^2 = c^2(t_2 - t_1)^2 - (x_2 - x_1)^2 - (y_2- y_1)^2$
-
光錐內部的所有點(如上圖中的事件B)都可以通過小於光速的速度與當前事件建立因果聯繫,它們與當前事件的間隔被稱作類時間隔
$s^2 = c^2(t_2 - t_1)^2 - (x_2 - x_1)^2 - (y_2 - y_1)^2 - (z_2 - z_1)^2 < 0$
-
光錐表面上的所有點都可以通過光速與當前事件建立因果聯繫,它們與當前事件的間隔被稱作類光或零性間隔
$s^2 = c^2(t_2 - t_1)^2 - (x_2 - x_1)^2 - (y_2 - y_1)^2 - (z_2 - z_1)^2 = 0$
-
光錐外部的所有點(如上圖中的事件C)都無法與當前事件建立因果聯繫,它們與當前事件的間隔被稱作類空間隔
$s^2 = c^2(t_2 - t_1)^2 - (x_2 - x_1)^2 - (y_2 - y_1)^2 - (z_2 - z_1)^2 > 0$
當然這和 Minkowski 空間的定義有關,如果是定義 (+,-,-,-), $s^2$ 的正負就剛好相反。