Math AI - Stochastic Differential Equation

Posted on | In

Reference

Lebesgue integral

https://en.wikipedia.org/wiki/Lebesgue_integration @wikiLebesgueIntegration2023: Lebesgue 積分英文

https://zh.wikipedia.org/zh-tw/%E5%8B%92%E8%B2%9D%E6%A0%BC%E7%A9%8D%E5%88%86 : 中文

@shionStochasticDynamic2021

https://zhuanlan.zhihu.com/p/343129740

[@ccOneArticle23]. https://zhuanlan.zhihu.com/p/589106222 very good article!!! SDE for diffusion score

什麽是隨機微分方程 (SDE)

在幾乎所有領域，如物理，化學，生物，氣象，金融及其許多工程分支，包括機械，航天，土木，電氣工程中，動力學系統的建模與分析都是一個關鍵性任務。在建模過程中,鑒於各種原因，如系統參數的可能變化，激勵的變化，建模方案的誤差等，不確定性是不可避免的。當我們學過《高等數學》或《常微分方程》等課程之後，可知確定性激勵作用下的狀態方程是確定的，若對某一不確定性有足夠大量數據，就可用概率與統計描述該不確定性。

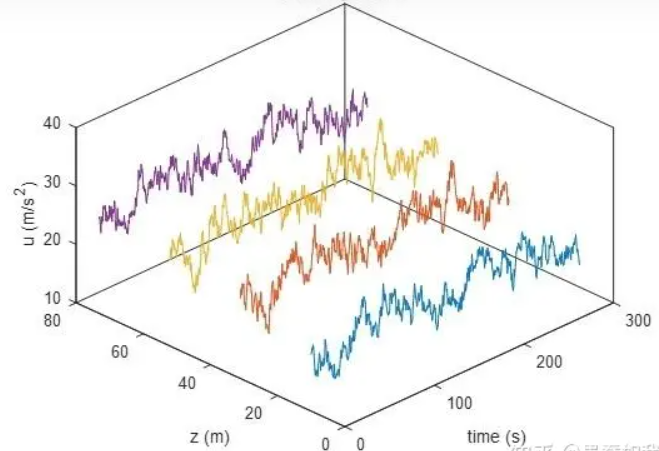
image-20230416153819560

Diffusion process 也是 SDE 的一種。

例一：(Time Derivative) Input/Output

SDE 的關鍵: 外部作用力 + random noise

一个单自由度弹簧系统，在外激励作用下的振动方程如下

\[\begin{aligned} & m \ddot{x}+c \dot{x}+k x=F(t) \\ \end{aligned}\]

当外激励为随机过程时候，相对于确定性激励

\[\begin{aligned} & \tilde{F} (t)=F(t) + \text{"noise"} \end{aligned}\]

引入变量 $X=[x, \dot{x}]^T=\left[x_1, x_2\right]^T$ ，将原方程改写为 (一階) 状态方程，即

\[\begin{aligned} \dot{X}=A X+N \tilde{F} (t) \end{aligned}\]

将 $dt$ 除过去可得 $d X=A X d t+N \tilde{F} (t) d t$

  1. 若 $\tilde{F} (t)=0$ ，即系统无外部激励（自由振动)， 原方程为 $d X=A X d t$

  2. 若 $F(t) \neq 0$ ，即系统受外激影响，原方程为随机微分方程，SDE.

例二：(Time Derivative) Hidden State/Output Estimation

Linear state space dynamic equation:

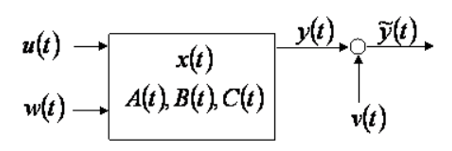image-20230416225852667 \(\begin{aligned} & \dot{x}=A x+B u+w \\ & y=C x \\ & \widetilde{y}=y+v \end{aligned}\)

  • 稱為 $A, B, C, D$ matrix (此處 $D=0$)
  • 此處 $u$ 是 input control, $w$ 是 input or state (stochastic) noise.
  • $y$ 是 true output, $\widetilde{y}$ 是 noisy output, $v$ 則是 output observation (stochastic) noise.

對應的 Kalman-Bucy Filter 用於 estimate $x(t), y(t)$, 就是連續版的 Kalman filter.

Kalman filter 的關鍵: SDE 的 hidden state/output 的 estimation

image-20230416230631540 \(\begin{aligned} & K=P C^T R^{-1} \\ & \dot{\hat{x}}=A \hat{x}+B u+K(\widetilde{y}-C \hat{x}) \\ & \dot{P}=A P+P A^T-K R K^T+Q \end{aligned}\)

  • 此處 $P$ 是 covariance of the measurement error ($v$), $Q$ 是 covariance of state error $w$.

前例基本都是假設信號本身是 deterministic, 只是被 “noise” 影響。

一般這類 “noise” 也假設是 Gaussian noise.

接下來我們要看一些不同的看法，就是信號本身就是 probablistics! 例如簡單的布朗運動，或是更複雜的影像分佈。我們要用更深入的數學, SDE, 描述這個現象！

另外是 “driving force”, 最簡單是 linear ODE. 看起來好像非常簡單。實務上 x 是 1D/2D vectors, 甚至 high dimension tensors, A 是 matrix/tensors, 可以有很多的 spatial 變化。如果 A 是 diagonal matrix 就很簡單。

但是 A 可以是 2D x vector 的差異，類似梯度 (gradient), 或是 divergence, curl 或是空間的微分 operators.

例三：(Time Derivative) Input/Output

布朗運動的關鍵: SDE 的 (外部) 作用力 = random noise

例四：(Time and Space Derivative!) Diffusion Process (Wrong!!)

(YES!) Diffusion process 的關鍵：SDE 的作用力來自 concentration gradient (濃度的梯度)，而非外部作用力。但濃度又是 SDE 的 variable. 所以是個互相影響的過程。 \(\frac{d x_t}{dt} = f(x_t) = D \nabla_{x_t} \log p_t(x_t)\)

Wrong!! 這是把 sample equation 和 distributin 搞混了。

Sample equation 的形式對應的解就包含 Fokker-Planck equation, 其中就有 diffusion term.

SDE 微分問題 - 標準型

隨機信號很多是連續但不可微分！一個例子就是布朗運動，數學上是處處不可微分。

所以一般不會寫成 $dX/dt = \mu(X, t)$, 而是 $dX = \mu(X, t) dt$.

從 Linear state space system 出發 : $\dot{x}=A x+B u+ w$

魔改成 stochastic dynamical system:

\[\begin{align} d X_t = a(X_t, t) dt + b(X_t, t) d W_t. \end{align}\]

此處 $a, b, W$ 對應 linear state space 的 $A, B, w$

  • $dt$ 都移到右邊。因為要考慮不可微分
  • $a, b$ 變成 function 以及包含 $t$, 而不是 linear time invariant matrix.
  • $b(X_t, t) d W_t$ 取代 $Bu +w$! 把 stimulus 和 noise 結合在一起。同時把 $w dt$ 改成 $dW_t$ .

(8) 是 general case. 我們考慮特例

  • $a(X_t, t)$ 稱為 drift coefficient; $b(X_t, t)$ 稱為 noise coefficient (drive diffusion).
  • SDE 稱為 stationary if $a, b$ 沒有 explicit $t$ dependent.
  • 如果 $b$ is independent of $x$, 稱為 additive noise. 如果 $b$ depends on $x$, 稱為 multiplicative noise.
  • 如果 $b(X_t,t) = 0$, SDE 就變成 ODE.

例二：(Time Derivative) 布朗運動

\[\begin{align} d X_t = \mu X_t \, dt + \sigma \, X_t \, d W_t. \end{align}\]

這是就簡單的 SDE.

SDE 微分和積分表示法

不妨设 $\tilde{F} (t)=W(t)$ ，引入关系式 $d B_t=W(t) d t$, 即上述随机状态方程可以改写为 $d X=A X d t+N d B_t$ 考虑受 Guass 白噪声扰动的一维动态系统，其运动微分方程形为 \(d X(t)=\mu(X, t) d t+\sigma(X, t) W(t) d t\) 式中 $\mu(X, t)=\mu[X(t), t], \sigma(X, t)=\sigma[X(t), t] ， \mathrm{~W}(\mathrm{t})$ 为单位强度的Guass白噪声。

  • $\mu(X, t)$ 稱爲 drift coefficient
  • $\sigma(X, t)$ 稱爲 diffusion coefficient

此方程 等价于下列积分方程: \(X(t)=X_0+\int_{t_0}^t \mu[X(s), s] d s+\int_{t_0}^t \sigma[X(s), s] W(t) d s\)

右邊第一個積分可解釋為均方或 sample 的 Riemann 積分。而第二個積分，利用在廣義隨機過程意義上 Gauss white noise 為 Wiener process 的導數性質，可以改寫成 \(\int_{t_0}^t \sigma[X(s), s] W(t) d s = \int_{t_0}^t \sigma[X(s), s] d W(s)\)

Ito 微分方程形为 \(d X(t)=\mu(X, t) d t+\sigma(X, t) d W(s)\) Ito 積分方程形为 \(X(t)=X_0+\int_{t_0}^t \mu[X(s), s] d s+\int_{t_0}^t \sigma[X(s), s] d W(s)\)

以上都是 Sample 的微分或是積分方程式，Sample 是無法直接計算的，除了用 Monte Carlo 模擬。

但是和 probability distribution 的關係是什麽？

另一個常用的統計特性是 auto-correlation function, 可以得到不同時間 samples 的 correlation. 另外 FFT 之後可以得到 spectrum (如果是 stationary process).

Random variable/process 的統計特性 (i.e. probability distribution) 則是可計算的，至少理論上如此。

很自然我們會問 (9) 或 (10) 的 probability distribution $p_t(X_t)$ 是如何隨著時間變化?

這是 Fokker-Planck equation 討論的問題。

Ito SDE 是比較 general 的 equation. Fokker-Planck equation 則是其解。

Fokker-Planck Equation

有兩種 approaches, 一個是科學空間的方法。另一個是 Wiki Fokker-Planck equation。

Approach 1: Wiki Fokker-Planck Equation

https://en.wikipedia.org/wiki/Fokker%E2%80%93Planck_equation

image-20230423225257185

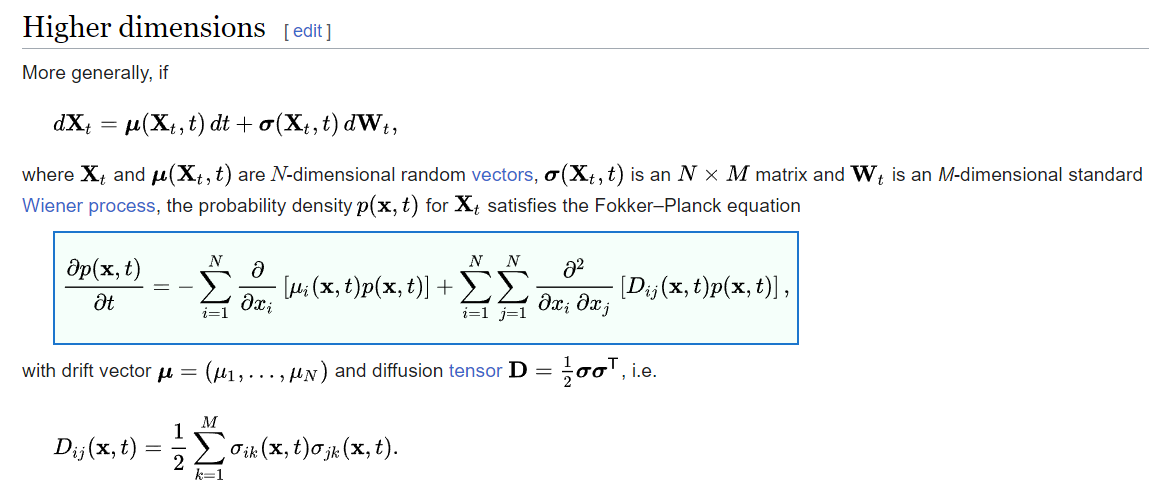
Higher diemsnions

image-20230423230936970

Approach 2: 科學空間方法

看起來像是 Drift Only Equation? 非常神奇，應該有問題，他好像把 drift and diffusion 混在一起！

下面的 equation (10) 似乎有問題。應該是保留第二項 (drift=0), 可以得到一個 diffusion only solution!!

以下的推導可以參考科學空間：https://spaces.ac.cn/archives/9280

先看簡化版，沒有 Wiener process 部分：

image-20230423230102277

image-20230423230217120

再來考慮 general case “Ito SDE”

对于SDE \(d \boldsymbol{x}_t=\boldsymbol{f}_t\left(\boldsymbol{x}_t\right) d t+g_t d \boldsymbol{w}\) 根据测试函数法的相等原理得 \(\frac{\partial p_t\left(\boldsymbol{x}_t\right)}{\partial t}=-\nabla_{\boldsymbol{x}_t} \cdot\left(p_t\left(\boldsymbol{x}_t\right) \boldsymbol{f}_t\left(\boldsymbol{x}_t\right)\right)+\frac{1}{2} g_t^2 \nabla_{\boldsymbol{x}} \cdot \nabla_{\boldsymbol{x}} p_t(\boldsymbol{x})\) 这就是“Fokker-Planck方程”。

image-20230418230646056

image-20230422210628461

image-20230422213034081

  • $p(x_t) = p_0(x_0) * N(x_t)$ convolution

  • $p_0(x_0)$ 就是原始的 distribution, 例如點熱源或是 image distribution, 不是 Gaussian! 但是 mixed Gaussian distribution 如 (13)：每一個 $x_0$ 對應一個 Gaussian.

  • 如果 $t$ 很小，$\sigma \to 0$, Gaussian kernel $N(x_t)$ 基本就是 delta function, $p(x_t)_{t=0} = p_0(t)$.

  • 當 $t$ 越來越大，$\sigma$ 越來越大，Gaussian kernel $N(x_t)$ 變成非常寬，但是 frequency domain 非常窄。所以非常接近 Gaussian kernel!!

以上就是 diffusion process, 不論是 thermal diffusion 或是 image diffusion process!

(2) 和 (12) 其物理意義類似有一個 (probability) flow in space 如下面的例子。

Thermal flow = probability flow

Transport Equation of Flux

有趣的是，$V$ 和 $\phi$ 常常都有簡單的關係，稱爲 transport equation (spatial dependent)。以下是一些 flow 例子：

Diffusion Flow

Continuity equation, 也代表質量守恆 equation. \(\nabla \cdot \mathbf{J} + \frac{\partial \varphi}{\partial t} = 0 \label{DiffCont} \quad \to \quad \frac{\partial \varphi}{\partial t} = - \nabla \cdot \mathbf{J}\) where

  • $\mathbf{J}$ is the diffusion flux, measures the amount of substance that will flow through a unit area during a unit time interval.

  • φ (for ideal mixtures) is the concentration, of which the dimension is amount of substance (mole) per unit volume.

再來因爲 diffusion flux 是 irrotational flow, $\nabla \times \mathbf{J} = 0$, 而且 potential $V$, $-\nabla V = \mathbf{J}$. 也就是驅動 diffusion flux 的勢能 $V$. 在 diffusion flux 的例子，$V$ 剛好正比于 $\varphi$, 也就是 $ V = D \varphi \rightarrow \mathbf{J} = -\nabla V = -D \nabla \varphi$. 這個比例常數, $D$, 稱爲 diffusion constant.

這就是 Fick’s first law, 也稱爲 transport law. \(\mathbf{J} = - D \nabla \varphi \label{Fick1}\) 爲什麽不是用 $V$ 取代 $\varphi$, 把比例常數放在另一邊，such as $\varphi = D’ V \to D’ \mathbf{J} = -\nabla V$? 主要的原因是 continuity equation including $\mathbf{J}$ and $\varphi$ 更基本，而 $V$ and $D = V / \varphi$ 則 depends on material and environment (e.g. 溫度，溶劑)，如下表。

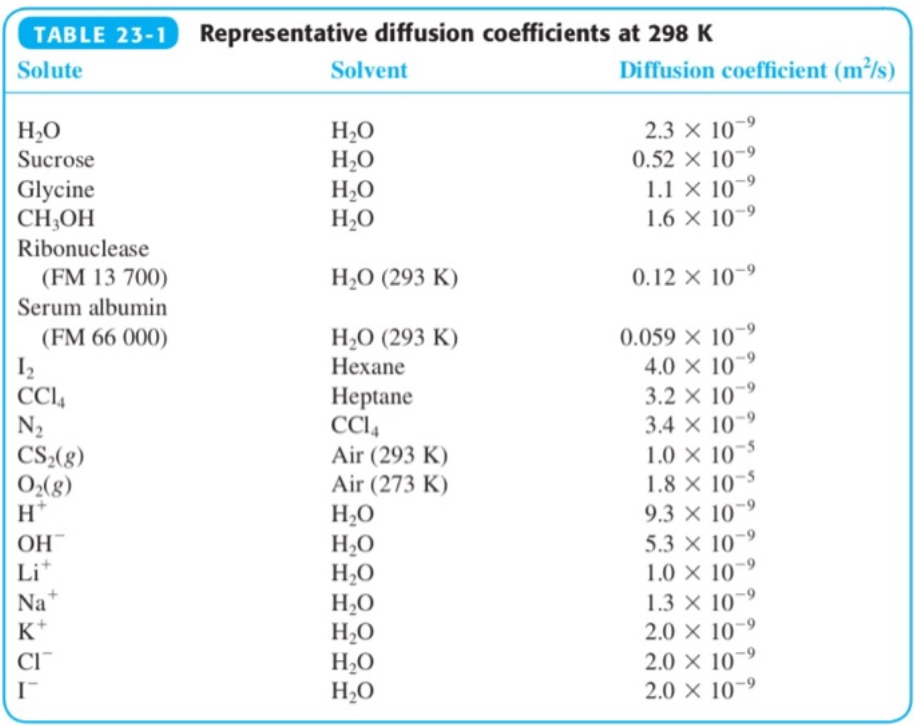
image-20220121233006496

$D$ 除了反應 material 和 environment 的特性，另一個功能吸收收 $V$ and $\varphi$ 單位的差異, area per unit time $L^2/T$, or SI 單位 $m^2/s$. 對於類似的 transport phenomen都是同樣的單位，

結合 continuity equation 和 transport law，就得到有名的 Fick’s second law (or transport equation) PDE (partial differential equation) with Laplacian operator. 在 Steady state 就化簡成 Laplacian equation. \(\frac{\partial \varphi}{\partial t} = D \nabla ^ 2 \varphi = D \Delta \varphi \label{Fick2}\)

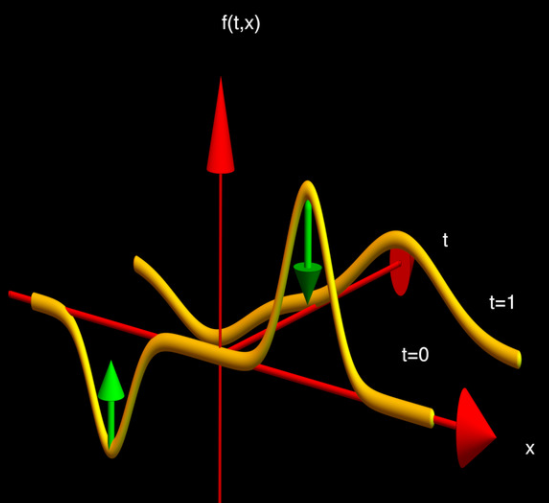
我們可以推論一下 $\varphi$ 的定性分析。我們簡化 $\nabla^2 \varphi = \Delta \varphi$ 為 1D spatial domain, 物理意義就是曲率。

  • 對於凸函數曲率為負值，因爲 $D$ 是正值，所以代表 $\varphi$ 對時間的微分為負值。因此凸函數隨時間變平緩，如下圖右半。
  • 對於凹函數曲率為正值，因爲 $D$ 是正值，所以代表 $\varphi$ 對時間的微分為正值。因此凹函數隨時間變平緩，如下圖左半。
  • 因此隨時間增加，山峰會平緩，山谷也會變平坦。這和熱或擴散的物理直覺一致，會到達熱平衡或濃度平衡。

image-20220126223206231

$\eqref{Fick2}$和 heat equation $\eqref{HeatEq}$ 其實一模一樣。只是把 diffusion constant $D$ 改成 thermal conductivity $k$。上式 fundmantal solution 稱爲 (heat) kernel. 基本是 variance 隨時間變大的 Gaussian function. 當然 PDE 具體問題的解 depends on the boundary condition.
\(\varphi(x, t)=\frac{1}{\sqrt{4 \pi D t}} \exp \left(-\frac{x^{2}}{4 D t}\right) \label{HeatKern}\)

最後一步，如何求解 flux vector field? 只要把 scalar field $\varphi$ 取 gradient in $\eqref{Fick1}$ 就可以得到 flux vector field $\mathbf{J}$.

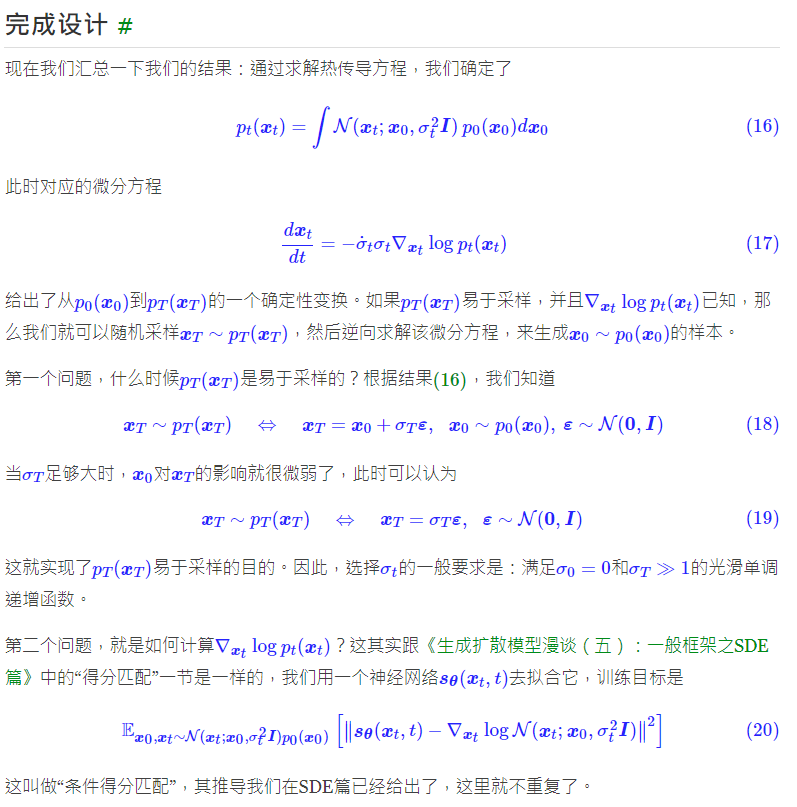
image-20230422222902030

神經網絡就是去擬合 score function of a normal distribution? 這應該只是 forward path? 不過如果是 deterministic function, 爲什麽需要神經網絡擬合？

應該是用神經網絡去擬合 $\nabla_{x_t} \log p(x_t) $

Linear SDE (Ito Lemma)

前文使用 DDPM 的角度解釋 Diffusion Model. 類似 VAE.

這裡使用 SDE 推導 Diffusion Model. 基本是用 neural network 近似 score function (gradient log P)

image-20230419230706390

image-20230419231017919

image-20230419231104936

image-20230419232224405

image-20230419232311935

Appendix

Appendix A: Ito SDE to Fokker-Planck Equation

对于 SDE \(d \boldsymbol{x}_t=\boldsymbol{f}_t\left(\boldsymbol{x}_t\right) d t+g_t d \boldsymbol{w}\) 我们离散化为 \(\boldsymbol{x}_{t+\Delta t}=\boldsymbol{x}_t+\boldsymbol{f}_t\left(\boldsymbol{x}_t\right) \Delta t+g_t \sqrt{\Delta t} \varepsilon, \quad \varepsilon \sim \mathcal{N}(\mathbf{0}, \boldsymbol{I})\) 那么 \(\begin{aligned} \phi\left(\boldsymbol{x}_{t+\Delta t}\right) & =\phi\left(\boldsymbol{x}_t+\boldsymbol{f}_t\left(\boldsymbol{x}_t\right) \Delta t+g_t \sqrt{\Delta t} \varepsilon\right) \\ & \approx \phi\left(\boldsymbol{x}_t\right)+\left(\boldsymbol{f}_t\left(\boldsymbol{x}_t\right) \Delta t+g_t \sqrt{\Delta t} \varepsilon\right) \cdot \nabla_{\boldsymbol{x} t} \phi\left(\boldsymbol{x}_t\right)+\frac{1}{2}\left(g_t \sqrt{\Delta t} \varepsilon \cdot \nabla_{\boldsymbol{x} t}\right)^2 \phi\left(\boldsymbol{x}_t\right) \end{aligned}\) 两边求期望, 注意右边要同时对 $\boldsymbol{x}_t$ 和 $\boldsymbol{\varepsilon}$ 求期望, 其中 $\boldsymbol{\varepsilon}$ 的期望可以事先求出, 结果是 \(\phi\left(\boldsymbol{x}_t\right)+\Delta t \boldsymbol{f}_t\left(\boldsymbol{x}_t\right) \cdot \nabla_{\boldsymbol{x}_t} \phi\left(\boldsymbol{x}_t\right)+\frac{1}{2} \Delta t g_t^2 \nabla_{\boldsymbol{x} t} \cdot \nabla_{\boldsymbol{x}_t} \phi\left(\boldsymbol{x}_t\right)\) 于是 \(\begin{aligned} & \int p_{t+\Delta t}\left(\boldsymbol{x}_{t+\Delta t}\right) \phi\left(\boldsymbol{x}_{t+\Delta t}\right) d \boldsymbol{x}_{t+\Delta t} \\ \approx & \int p_t\left(\boldsymbol{x}_t\right) \phi\left(\boldsymbol{x}_t\right) d \boldsymbol{x}_t+\Delta t \int p_t\left(\boldsymbol{x}_t\right) \boldsymbol{f}_t\left(\boldsymbol{x}_t\right) \cdot \nabla_{\boldsymbol{x}_t \phi} \phi\left(\boldsymbol{x}_t\right) d \boldsymbol{x}_t+\frac{1}{2} \Delta t g_t^2 p_t\left(\boldsymbol{x}_t\right) \nabla_{\boldsymbol{x}_t} \cdot \nabla_{\boldsymbol{x}_t} \phi\left(\boldsymbol{x}_t\right) d \boldsymbol{x}_t \end{aligned}\) 跟式 $(13)$ 、式 $(14)$ 类似，取 $\Delta \rightarrow 0$ 的极限, 得到 \(\int \frac{\partial p_t\left(\boldsymbol{x}_t\right)}{\partial t} \phi\left(\boldsymbol{x}_t\right) d \boldsymbol{x}_t=\int p_t\left(\boldsymbol{x}_t\right) \boldsymbol{f}_t\left(\boldsymbol{x}_t\right) \cdot \nabla_{\boldsymbol{x}_t} \phi\left(\boldsymbol{x}_t\right) d \boldsymbol{x}_t+\frac{1}{2} g_t^2 p_t\left(\boldsymbol{x}_t\right) \nabla_{\boldsymbol{x}_t} \cdot \nabla_{\boldsymbol{x}_t} \phi\left(\boldsymbol{x}_t\right) d \boldsymbol{x}_t\) 对右边第一项应用式 $(6)$ 、对右边第二项先应用式(7)再应用式 $(6)$, 得到 \(\int \frac{\partial p_t\left(\boldsymbol{x}_t\right)}{\partial t} \phi\left(\boldsymbol{x}_t\right) d \boldsymbol{x}_t=\int\left[-\nabla_{\boldsymbol{x}_t} \cdot\left(p_t\left(\boldsymbol{x}_t\right) \boldsymbol{f}_t\left(\boldsymbol{x}_t\right)\right)+\frac{1}{2} g_t^2 \nabla_{\boldsymbol{x}} \cdot \nabla_{\boldsymbol{x}} p_t(\boldsymbol{x})\right] \phi\left(\boldsymbol{x}_t\right) d \boldsymbol{x}_t\) 根据测试函数法的相等原理得 \(\frac{\partial p_t\left(\boldsymbol{x}_t\right)}{\partial t}=-\nabla_{\boldsymbol{x}_t} \cdot\left(p_t\left(\boldsymbol{x}_t\right) \boldsymbol{f}_t\left(\boldsymbol{x}_t\right)\right)+\frac{1}{2} g_t^2 \nabla_{\boldsymbol{x}} \cdot \nabla_{\boldsymbol{x}} p_t(\boldsymbol{x})\) 这就是”Fokker-Planck方程”。