Reference
Youtube video: 4.2 Accelerated Gradient Descent - YouTube UT Austin: Constantine Caramanis. Very good series.
Background
Optimization 是非常有趣的問題。看似無常形無常法。
例如可以把 constraints 變成 Lagrange multiplier
$\min_x f(x)$ s.t. $g(x)=0$ $\to$ $\min_{x, \lambda} \mathcal{L}(x, \lambda) = f(x) + \lambda g(x)$
除了標準形,理論上也可以做各種變形
$\min_{x, \lambda} \mathcal{L}(x, \lambda) = f(x) + \lambda | g(x)|^2$
或是 $\min f(x) + \lambda_1 g(x) + \lambda_2 |g(x)|^2$ … 等等
或是把一個 domain optimization 換到另一個 domain optimization.
一個概念是把 time domain 的 optimization, 例如最小化振幅,轉換 (Fourier transform) 成 frequency domain 的 optimization, 例如最大化頻譜。注意這裏只是概念,系統的 domain 轉換就是 primal-dual optimization. 或是 Legendre transform 的 optimization.
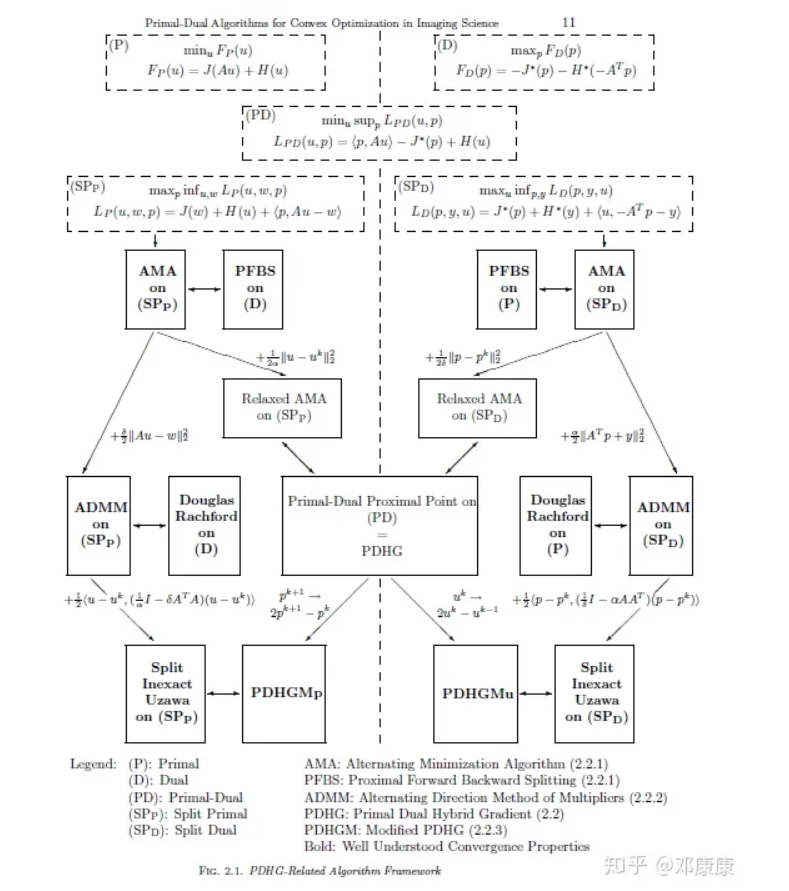
對於 convex optimization, 還是可以整理出一個框架 (framework)。
Primal-Dual Framework
Convex optimization 有所謂 primal and dual problem.
有幾種不同的 primal-dual formulation.
第一類就是最常見的 Lagrange duality.
第二類是 conjugate duality.
所謂的 primal-dual 都是 $\min \max$ 和 $\max \min$ or $\inf \sup$ 和 $\sup \inf$
Lagrange Duality

Conjugate Duality
第二種方法是利用 conjugate function 解釋 primal and dual.
先看 convex conjugate 定義:
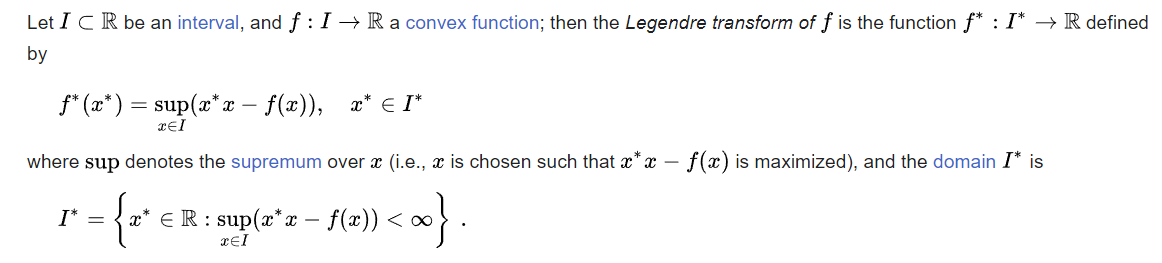
上面的定義太數學了。我們看幾何的意義。用最單純的二次函數爲例:$f(x) = c x^2$
conjugate function: $f^* (x^{})= \sup(x^ x - f(x))$
conjugate function 定義包含 maximum: 因此 conjugate function 的 input $x^* = f’(x)$, 也就是原函數的斜率。$f^(x^)$ 的值就是通過 (x, f(x)) 切綫和 $y$ 軸的截距。可以證明 conjugate 是 concave (-convex) function. 所以也稱爲 convex conjugate.
既然 conjugate 是 -convex function, 也可以找到 maximum (or minimum 如果乘 -1). 不過 conjugate optimization 和原始 function 的 optimization 有任何關係嗎? YES!
如下圖:
(P) Primal 問題: $\min_u F_P(u)$ 和 (D) Dual 問題: $\max_p F_D(p)$
可以結合成 min-max 問題?還蠻奇怪的。