Reference
Youtube video: 4.2 Accelerated Gradient Descent - YouTube UT Austin: Constantine Caramanis. Very good series.
Background
用 convex function 卻使用 gradient descent, sub-gradient method, momentum, etc. 得到更多的 insight!!
而不是用 2nd order statistics like Hessian 或是牛頓法!
這樣更有物理和數學 insights!!
Lesson Learned
Convex optimization 基本是所有 optimization algorithm 的鼻祖。Convex optimization 有非常高效率的 solutions for large scale 問題。
雖然很多問題本身不是 convex, 但可以轉換成 convex optimization 再利用現成的 solution.
另一個想法是利用 convex function 驗證 algorithm!!
Convex, Smooth, Strict Convex 定義
完整的凸函數包含兩個部分:convex domain ($\R^n$) + convex function ($\R^n\to\R$)
-
(Constrained) domain $C \subset \R^n$ 是 convex set (凸集):
$x_1, x_2 \in C \, \to \, t x_1 + (1-t) x_2 \in C$ where $0\le t \le 1$
- Unconstraint domain $C = \R^n$ 也是 convex set.
-
Convex function:
\[x_1, x_2 \in C \,\to \, f\left(t x_1 + (1-t) x_2\right) \le t f(x_1) + (1-t) f(x_2)\]
擴展 convex function 其他等價定義: Convex function 有下列等價定義
- $f(x)$ 是一個 a convex function ($\R^n\to \R$) + domain ($C \subset \R^n$) 是 convex set
- $\text{epi-}f$ 是一個 convex set in $\R^{n+1}$! i.e. $x’_1, x’_2 \in \text{epi-}f\, \to \, t x’_1 + (1-t) x’_2 \in \text{epi-}f$ where $0\le t \le 1$
什麽是 Epigraph (Epi - on ; graph - write)?
epi-$f$ 幾何顯示如下圖。就是 $f(x)$ (含) 以上所包含的藍色區域,非常直覺。
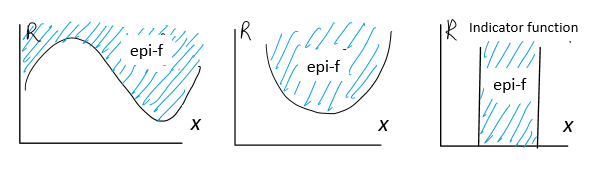
這個例子顯示:epi-$f$ 的維度是: 定義域維度 (1D) + 值域維度 (1D) = 2D (in these cases)
-
$f(x)$ 的定義域是 n 維凸集,epi-$f$ 是 n+1 維凸集。
-
幾何圖形更清楚。就是所有 $f(x)$ 以上畫藍色的區域 (2-D)。注意定義域 $x$ 是 1-D, 值域也是 $1$-D. 但是藍色的 epi-f 是 2D.
Epi-$f$ 有什麽用途? 可以把凸函數 (convex function) 和凸集 (convex set) 結合一起。
-
左圖:$f(x)$ 顯然是非凸函數,對應的 epi-$f$ 是非凸集。可以證明反之也爲真!
-
中/右圖: $f(x)$ 是凸函數,則 epi-$f$ 是凸集。
| Epigraph 的正式定義: $\text{epi-}f = {(x,t) | x \in \text{dom} f, f(x) \le t}$ |
-
因爲 $x \in \text{dom}f \subset \R^n$, $t \in \R \to$ $(x, t) \in \R^{n+1}$. 也就是 $\text{epi-}f$ 是 n+1 維度的 set.
-
(Bad explanation:值域找定義域) 對於任意 $t \in \R$, 就是找出所有 $x \in \text{dom}f$ 滿足 $f(x) \le t$.
- 顯然如果 $t < \min f(x)$, 沒有任何 $(x, t)$ 滿足 $f(x)\le t$
- 隨著 $t$ 變大,開始存在 $(x,t)$ such that $f(x) \le t$.
-
(Right explanation:定義域找值域) 對於任意 $x \in \text{dom}f$ 找到所有 $t \ge f(x)$
-
如何把定義域和值域結合成新的 set? 我們可以定義 epigraph 的點是可以做 operation. $x’_1 + x’_2 = (x_1, t_1) + (x_2, t_2) = (x_1+x_2, t_1+t_2)$ and $a x’_1 = a (x_1, t_1) = (a x_1, a t_1)$.
-
Epigraph 不是只有定義域 $\R^n$! 而是定義域 + 值域 $\R^{n+1}$!
Convex, Smooth, Strict Convex 幾何詮釋
Convex optimization: (unbounded) local minimum = global minimum
- Assume $f(x)$ is a convex and differentiable function. 幾何就是 $f(x)$ 在每點 $x_0$ 的切綫上。切綫是 lower bound.
\(f(x) \geqslant f(x_0)+ \nabla f \cdot (x-x_0) \quad \text{for } \forall x,x_0 \in C\)

- Assume $f(x)$ is convex but may not be differentiable, 可以使用 sub-gradient: 在 differentiable points gradient = sub-gradient ($g=\nabla f$), 在 non-differentiable points, 可以用 sub-gradient, $g$. Sub-gradient 形成的切綫是 lower bound.
- Assume $f(x)$ is Lipschitz $\beta$-smooth. 幾何上就是 $f(x)$ 在每點 $x_0$ 的切抛物綫下。切抛物綫是 upper bound.
\(f(x) \leqslant f(x_0)+\nabla f \cdot (x-x_0)+\frac{\beta}{2}\|x-x_0\|^2 \quad \text{for } \forall x,x_0 \in C\)
-
Assume $f(x)$ is strongly $\alpha$-convex. 幾何上就是 $f(x)$ 在每點 $x_0$ 的切抛物綫上。切抛物綫是 upper bound, 是比切綫更緊的 lower bound.
-
Assume $f(x)$ is strongly $\alpha$-convex and $\beta$-smooth. 幾何上就是 $f(x)$ 在每點 $x_0$ 都被兩個切抛物綫夾住,如下圖。 可以證明 $\beta > \alpha$ \(f(x) \geqslant f(x_0)+\nabla f \cdot (x-x_0)+\frac{\alpha}{2} \|x-x_0\|^2 \quad \text{for } \forall x,x_0 \in C\)

Use Proximal operator \(f(y) \geqslant f(x)+\operatorname{prox}(y-x) ?\)
Convex Optimization
Error, Convergence Rate
Sub-gradient method
- 1st order method: use subgradient (gradient = subgradient if differentiable)
- step size: variable, approach 0 after T iterations
Gradient descent
- 1st order method: use 1st derivative gradient
- step size: fixed
Newton method
- 2nd order method: use 2nd derivative
- step size: variable and based on Gradient and Hessian
| Convex | Convex + $\beta$-smooth | $\alpha$-strict Convex + $\beta$-smooth | |
|---|---|---|---|
| error | |||
| rate | |||
| oracle rate |
| Iteration | Error | ||
|---|---|---|---|
| sub-gradient method on convex | $O(1/\epsilon^2)$ | $O(1/\sqrt{T})$ | |
| gradient descent on convex | $O(1/T)$ | ||
| gradient descent on convex + smooth | |||
| gradient descent on $\alpha$-strict convex + $\beta$-smooth | $O\left(\left(\frac{K-1}{K+1}\right)^T\right)$ $K = \beta/\alpha > 1$ |
||
| Oracle lower bound on convex (Lipschitz continuous) | $O(1/\sqrt{T})$ | ||
| Oracle lower bound on convex + Lipschitz smooth | $O(1/T^2)$ | ||
| Oracle lower bound on strongly convex + smooth | $O\left(\left(\frac{\sqrt{K}-1}{\sqrt{K}+1}\right)^T\right)$ | ||
| Momentum gradient descent on convex + $\beta$-smooth | $O(1/T^2)$ | Nestrov | |
| Momentum gradient descent on $\alpha$-strict convex + $\beta$-smooth | $O\left(\left(\frac{\sqrt{K}-1}{\sqrt{K}+1}\right)^T\right)$ | ||
| Proximal gradient on convex | $O(1/T)$ | ||
| Proximal gradient on smooth and strongly convex |
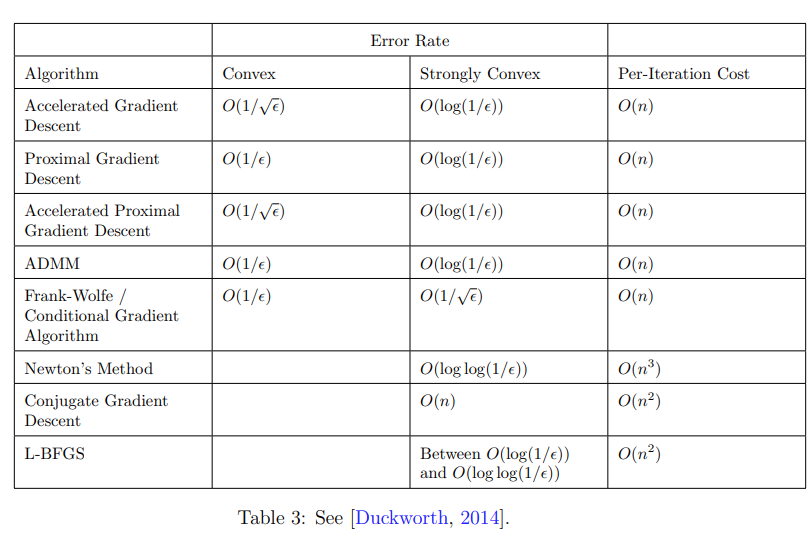
| Algorithm | Convex | Convex+ $\beta$-smooth |
$\alpha$-strongly Convex + $\beta$-smooth |
Per Iteration Cost |
|---|---|---|---|---|
| Sub-gradient method | $O(1/\epsilon^2)$ | |||
| Gradient Descent | $O(1/\epsilon)$ | |||
| Oracle lower bound | ||||
| Momentum GD | $O(1/\sqrt{\epsilon})$ | |||
| Proximal gradient |
Q&A : How about ADAM and other convergence algorithm on convex function, smooth, and strict convex + smooth????
For constraint problem, non-differentiable
projected subgradient

Stochastic subgradient optimization

Projection –> proximal operator

Proximal optimization
Legendre transform!!


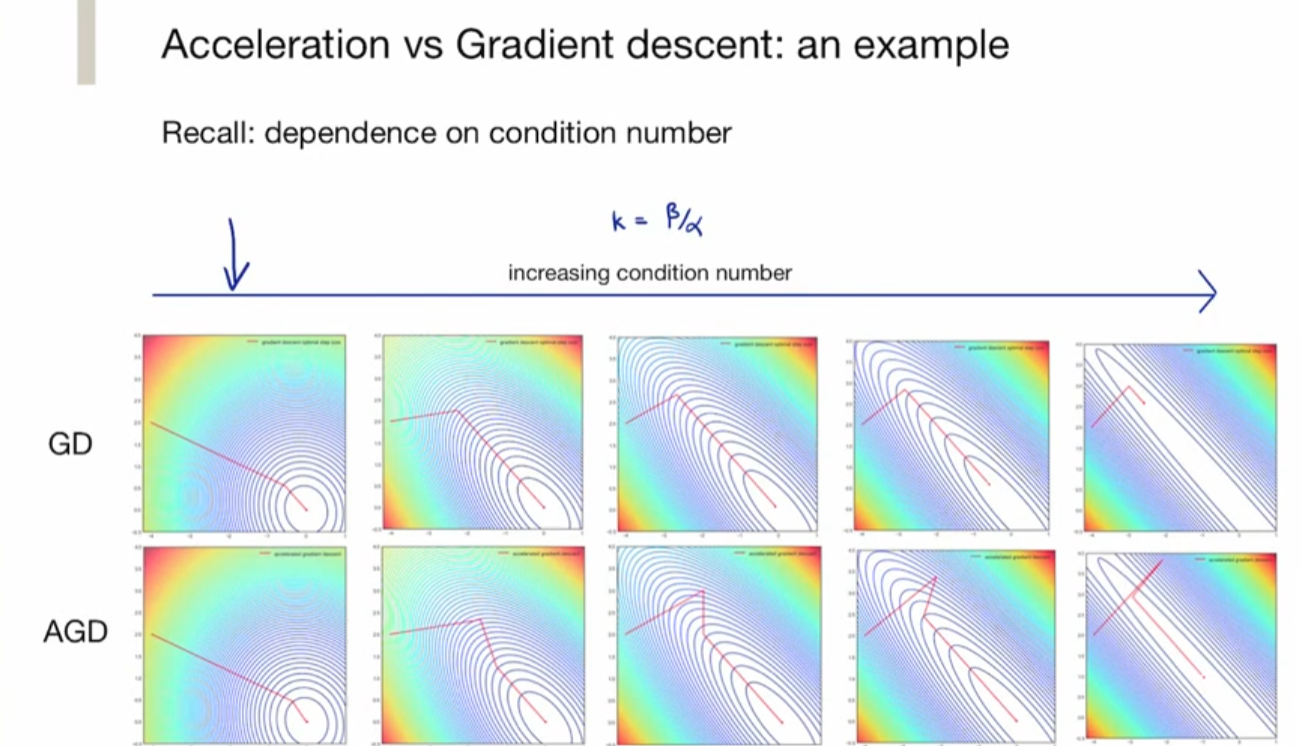
Momentum Method: to close the gap between GD vs. Oracle lower bound

K = b/a, 代表 max / min eigenvalues for quadratic function
Projections and Proximal Operators
