Source
YouTube
Background
Stochastic gradient descent
- Noisy Gradient
- Stochastic Optimization
- Random coordinate descent!
Noisy gradients
Instead of $\nabla f $, 我們得到的是 $E[g] = \nabla f$
Stochastic Optimization
問題描述
$\min: f(x)$, st: $x \in C$ 改成
$\min_x: E_\xi [f(x); \xi]$, st: $x \in C$
什麽是 $\xi$, 就是 machine learning 的 training parameter.
例如在 linear regression $\min_x E[(y - \xi^T x)^2]$
$(y_1, \xi_1), (y_2, \xi_2), …$ 就是 training data.
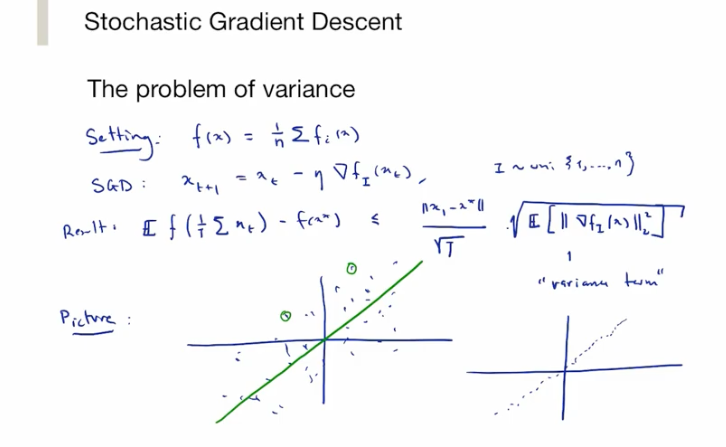
Empirical Risk Minimization Z(ERM) = $\min f(x) = \frac{1}{n} \sum f_i(x)$
在 classification 問題:
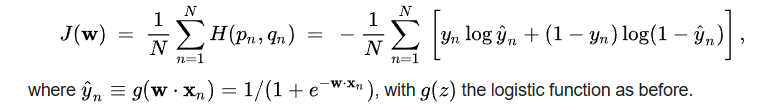
NO, 應該反過來。$x$ 最後是 training parameter 可以使用 gradient descent 得到。 $\xi$ 則是 data with distribution.
Full GD is very expensive! going over all data points.
SGD
GD 有 self-tuning 特性
sub-GD 沒有 self-tuning 特性
在 SGD 也是一樣?yes
Sub-gradient proportional to 1/sqrt(T)
Gradient descent proportional to 1/T
SGD 1/sqrt(T)

SGD is similar to sub-differential!!
No self-tuning for SGD