Optimization - Gradient Descent

Posted on | In

Source

  1. 非線性優化方法的總結: https://zhuanlan.zhihu.com/p/85423364?utm_id=0 很好的總結文章

  2. Why Momentum Really Works? [@gohWhyMomentum2017]

  3. MIT: overview of gradient descent: [@ruderOverviewGradient2016]

Introduction

本文討論 (convex) optimization 方法 $\min_x L(x)$, $x \in \R^n$

$L(x)$ 可以想成是一個 loss function. 我們的目的是找到 $n$ 維的 $x$, 一般稱爲 weight 極小化 loss function.

很多時候 $L(x)$ 是一個複雜的 function, 找到 $x_{min}$ 比 $L(x_{min})$ 更重要，而且只有近似的迭代法。

從 deterministic 到 stochastics，從一階到二階，從原始到對偶。光滑到非光滑。

迭代算法就是不斷逼近，化繁為簡，將一個個難問題分為若干個易問題的過程。

化繁為簡包含兩個角度

  1. 時間: 逐步逼近
  2. 空間: separable

image-20230527143734830

Deterministic Method

先看最常用而且簡單的方法，就是梯度法 (Gradient Descent).

一階方法：Gradient Descent

Gradient Descent (GD) 方法如下：
\(x_{k+1} = x_k - \alpha \nabla L(x_k)\)

GD 的重點

  • $x$ ,$\nabla L(x) \in \R^n$ 是向量。

  • $\alpha$ 是一個固定的純量。但是每次的 step: $\alpha \nabla L(x_k)$ 是 self-adjusted step.

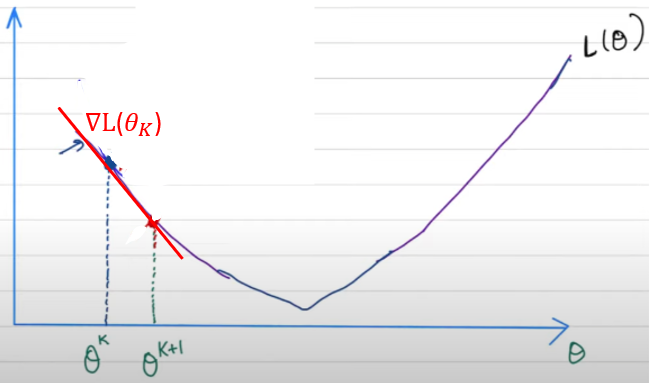
GD 幾何意義

我們回過來看 gradient descent (GD) 的幾何意義。

  • $L(x)$ 是 convex function

  • $L(x) \ge L(x_k) + \nabla L(x_k) (x-x_k)$ 這可以視爲 Taylor expansion approximation. 因爲 $L(x)$ 是 convex function, 所以大於等於 1st order Taylor expansion. 就是 $L(x)$ 的切綫下界 (lower bound).

  • 一般 GD : $x_{k+1} = x_k - \alpha \nabla L(x_k)$. 其中 $\alpha$ 稱爲 learning rate, 似乎只是隨意選擇的 parameter?

  • NO! 其實 $\alpha$ 有清楚的物理意義。就是 $L(x)$的一個 (potential 上界) 抛物綫。

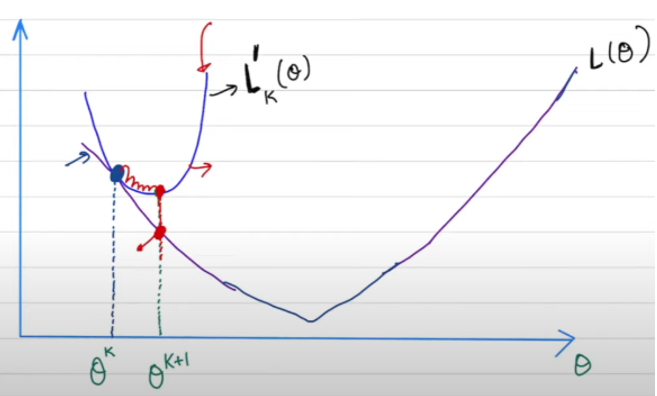
    image-20230527190011502

  • $f(x) \ge L(x) \ge L(x_k) + \nabla L(x_k) (x-x_k)$. 此處 $f(x)$ 是一個二次抛物綫，滿足
    1. $f(x_k) = L(x_k)$
    2. $\nabla f(x_k) = \nabla L(x_k)$
    3. $\nabla f(x_{k+1}) = 0$

  • 如何解 $f(x)$: $f(x)= a x^2+b x+ c = L(x_k) + \nabla L(x_k)(x-x_k) + k(x-x_k)^2 $ 滿足 1 and 2.

    • 代入 3. $\nabla L(x_k) + 2 k (x_{k+1} - x_k) = 0$, 也就是

    • $x_{k+1} = x_k - \frac{1}{2k} \nabla L(x_k) $. 比較 GD $x_{k+1} = x_k - \alpha \nabla L(x_k)$ 可以得到 $k = \frac{1}{2\alpha}$

    • $f(x)= L(x_k) + \nabla L(x_k)(x-x_k) + \frac{1}{2\alpha}(x-x_k)^2 $!!

    • 上式看起來是 Taylor expansion of 2nd order，不過其實不是。而 (預期) 是上界。

  • $L(x_k) + \nabla L(x_k)(x-x_k) + \frac{1}{2\alpha}(x-x_k)^2 \ge L(x) \ge L(x_k) + \nabla L(x_k) (x-x_k)$.

    • 如果 $\alpha$ 接近 0，上面的平方項一定可以滿足上界的要求！但是 GD 的 step 就非常小。
    • 如果 $\alpha$ 很大，大過某個 threshold，上面的平方項有可能變成下界而非上界！所以 GD 一個重要的任務就是要選擇 $\alpha$ 盡量大但是不能超過某個 threshold. 幾何上對應的就是比較緊的上界。

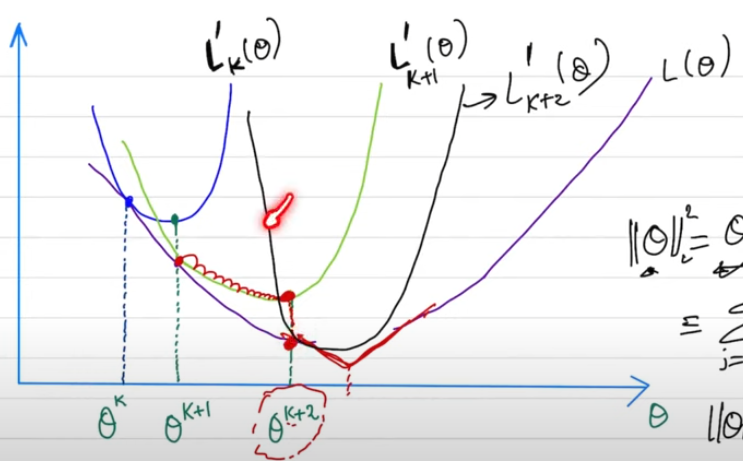
image-20230522213124947

定義域看 GD

根據以上幾何的詮釋，可以得到以下的迭代表示法：

$x_{k+1} = x_k - \alpha_k \nabla L(x_k) = \arg \min_x {L(x_k) + \nabla L(x_k)(x-x_k) + \frac{1}{2\alpha_k}(x-x_k)^2 } $

一般的 GD： $\alpha_k$ 會選擇一個常數，小於某個 threshold ~ $L(x_k)$ 曲率的倒數 (Hessian 的倒數)。如果 $L(x_k)$ 附近越接近直綫，$\alpha_k$ 可以越大，就是越 aggressive step.

$\alpha_k$ 也可以變成 optimization 的目標，比如最速下降法这样选择步长 \(\alpha^k=\arg \min _\alpha L\left(x^k-\alpha \nabla L\left(x^k\right)\right)\) 或者采用线搜索的形式找到一个满足线搜索的步长即可。更快速的步长为一种叫BB方法的步长 \(\alpha^k=\frac{\left(s^k\right)^T s^k}{\left(s^k\right)^T y^k},\) 其中 $s^k=x^k-x^{k-1}, y^k=\nabla L\left(x^k\right)-\nabla L\left(x^{k-1}\right)$ 。

这个步长其实是对Hessian矩阵倒數的一个近似，可以叫它伪二阶方法。BB步长及其有效，对于某些方法的提速有奇效，你可以在各种新的方法中看到它的身影。可惜不是单调的，对于一般非线性函数没有收敛性保障，所以通常会结合线搜索使用。

GD 收斂問題

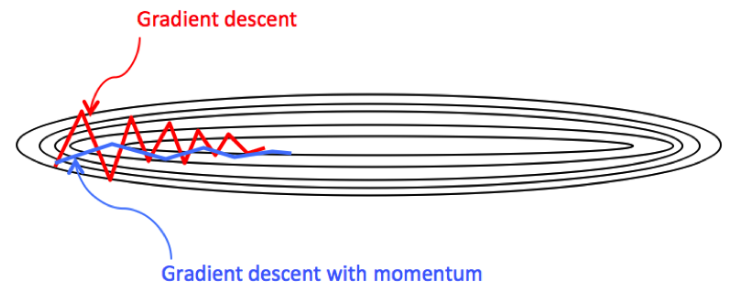
GD 最大的問題是多維空間 (即使 2D) 無法快速收斂！ 原因是多維空間只要有一維的曲率很大，如果 $\alpha$ 大於這個方向的曲率倒數，就會造成振盪非常久才收斂，甚至不收斂。

此時就要说一下共轭梯度方法，这个方法可以这样理解: 它觉得负梯度方向不好，所以去改良它，用上一步方向对它做一个矫正。共轭梯度方法其实动量方法还有heavy ball方法非常相似 \(\begin{aligned} & x^{k+1}=x^k+\alpha^k p^k \\ & p^{k+1}=-\nabla L\left(x^{k+1}\right)+\beta^k p^k \end{aligned}\)

比較 GD 和 momentum GD 方法的差異。我們用 2D 的等高圖來看。

[@gohWhyMomentum2017]

image-20230528084416171

二階方法：牛頓法

基本使用二階 Taylor expansion, 使用真的 Hessian 而非用上界抛物綫迭代近似。

首先对原函数做二阶泰勒展开，那么将得到二阶算法 \(\begin{aligned} x^{k+1} & =\arg \min \left\{L\left(x^k\right)+<\nabla L\left(x^k\right), x-x^k>+\frac{1}{2}\left(x-x^k\right)^T \nabla^2 L\left(x^k\right)\left(x-x^k\right)\right\} \\ & =x^k-\left(\nabla^2 L\left(x^k\right)\right)^{-1} \nabla L\left(x^k\right) \end{aligned}\) 这就是牛顿方法。

  • 和 GD 比較，牛頓法就是把 $\alpha_k$ 變成 Hessian 的倒數
  • 当维数太大时，求解Hessian矩阵的逆很费时间，所以我们就去用向量逼近，这 样就得到了拟牛顿方法, 这里就不讲了。
  • 有时候我们希望能够控制每一步走的幅度，根据泰勒展开的逼近程度来决定我们这一步要圭多远， 这样就得到了信赖域方法

\(\begin{aligned} & x^{k+1}=\arg \min \left\{L\left(x^k\right)+<\nabla L\left(x^k\right), x-x^k>+\frac{1}{2}\left(x-x^k\right)^T \nabla^2 L\left(x^k\right)\left(x-x^k\right)\right\} \\ & \text { s.t. } x-x^k \in \Delta^k \end{aligned}\) 这里的 $\Delta^k$ 为信赖域半径，如果泰勒展开逼近的好，我们就扩大半径，否则就缩小半径。 还有个类似于信赖域方法的叫cubic正则方法 \(\begin{aligned} x^{k+1}=\arg \min \left\{L\left(x^k\right)+<\nabla L\left(x^k\right), x-x^k\right. & >+\frac{1}{2}\left(x-x^k\right)^T \nabla^2 L\left(x^k\right)\left(x-x^k\right)+\frac{1}{\alpha^k} \| x \\ & \left.-x^k \|^3\right\} \end{aligned}\) 这个cubic正则项和信赖域有着差不多的功效。

Stochastic Method

我們把原來的問題重新 formulate to fit 常見的機器學習優化問題。

原始的問題: $\min_x L(x)$, $x \in \R^n$

在機器學習中，我們有 N 個 labeled data. Loss function 改成 $L(x) = \frac{1}{N}\Sigma_{i=1}^N f_i(x)$

$f_i(x)$ 可以是 regression loss function (L2 norm or logistic regression function), classification function (entropy function)。基本都是凸函數。

$\min_x L(x) = \min \frac{1}{N} \sum^N_{i=1} f_i(x) = \min_x \sum^N_{i=1} f_i(x)$, $x \in \R^n$

此處的 $N$ 是機器學習的 samples; $x$ 是 weights, $n$ 是 number of weight.

一般 N 非常大，可以是幾百萬。同時 $N \gg n$.

如果使用 GD, 每一次迭代，最低的代价也要算一次梯度。如果 N 很大的时候，算一次完整的函数梯度都费劲，这时候就可以考虑算部分函数梯度。如果這些 sample 都是 independent, 部分函數的梯度法也會收斂到完整函數的梯度法。

一階方法：Stochastic Gradient Descent (SGD)

\[\begin{aligned}x^{k+1} & =\arg \min \left\{f_{i_k}\left(x^k\right)+<\nabla f_{i_k}\left(x^k\right), x-x^k>+\frac{1}{2\alpha^k} \|x-x^k\|^2\right\} \\& =x^k-\alpha^k \nabla f_{i_k}\left(x^k\right)\end{aligned}\]

此處 $i_k \in 1, \cdots， N$

一個更常用的變形是 mini-batch, 也就是用多個 samples, 通常是 4/8/16/32/…/256, 計算 gradient.

其他一系列的 stochastic GD 變形

[@gohWhyMomentum2017]

Adam, Adadelta, Adagrad, RMSProp

Netsterov, AdamW

二階方法：sub-sample Newton Method

一阶方法的缺陷就是精度不够高，所以有时候还是需要用到二阶方法，但是呢，我们又嫌二阶方法太慢，所以干脆就对Hessian矩阵也采样，这样就得到了subsample Newton方法 \(\begin{aligned}x^{k+1} & =\arg \min \left\{f_{i_k}\left(x^k\right)+<\nabla f_{i_k}\left(x^k\right), x-x^k>+\frac{1}{2}\left(x-x^k\right)^T \nabla^2 f_{i_k}\left(x^k\right)\left(x-x^k\right)\right\} \\& =x^k-\left(\nabla^2 f_{i_k}\left(x^k\right)\right)^{-1} \nabla f_{i_k}\left(x^k\right)\end{aligned}\)

其他一系列的二階 stochastic GD 變形

Google: Lion, Tiger

Stanford: Sophia

Reference