Optimization - Proxmial Gradient Descent

Posted on | In

Source

  1. 非線性優化方法的總結: https://zhuanlan.zhihu.com/p/85423364?utm_id=0 很好的總結文章

  2. Stanford: Proximal Algorithms [@boydProximalAlgorithms2013]

Introduction

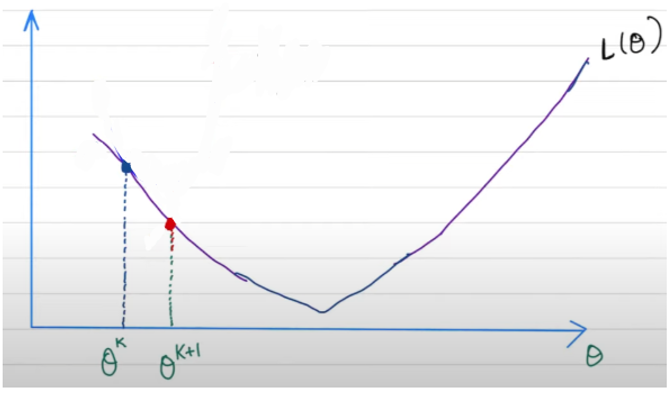
(Convex) optimization 的問題之一是不可微分，如下圖 1D 最小值點不可微分。

image-20230521091158849

或是如下圖 2D $\min_x f(x) = |Aw+b|^2 + \lambda \vert w \vert$， 此處 $w = (w_1, w_2)$

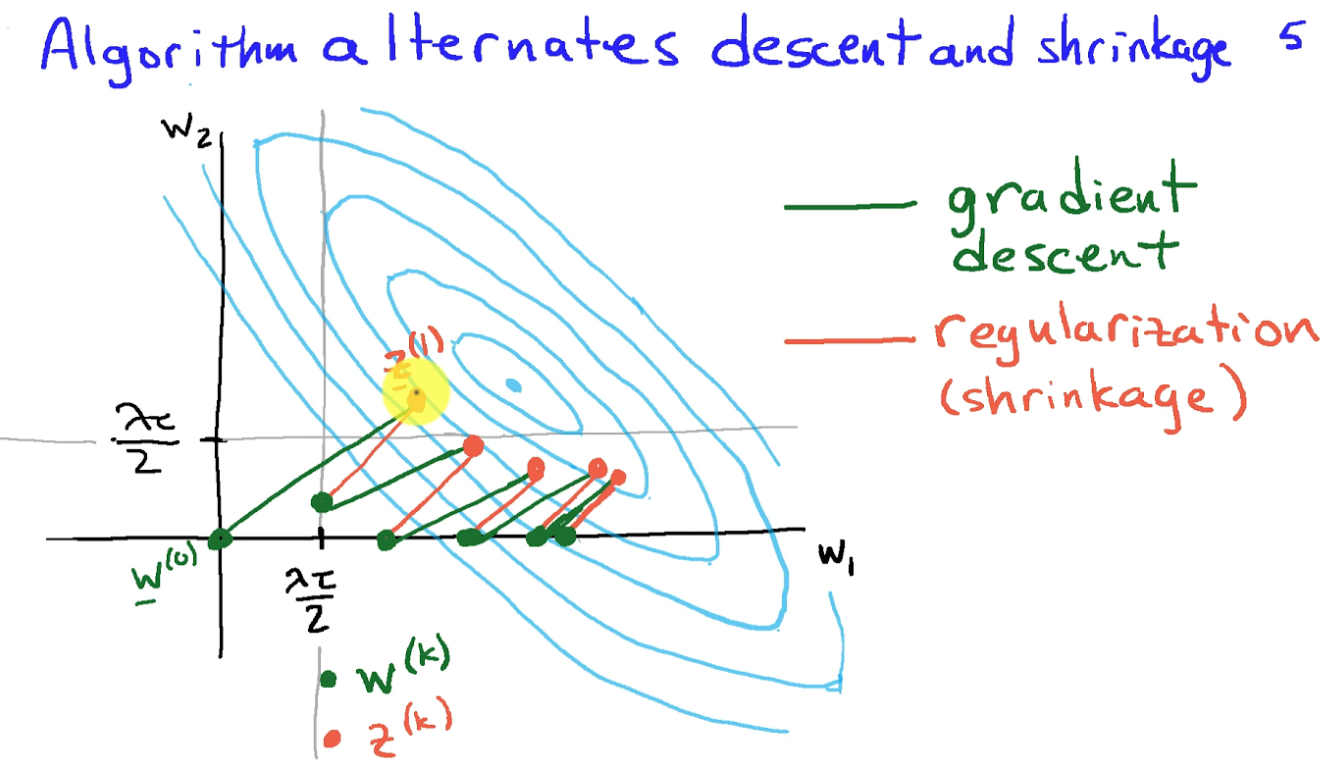
image-20230528090349216

傳統的 gradient descent (需要一階微分) 或是 Newton method (需要一階和二階微分) 在基本無法收斂！

如何解決不可微分問題?

一個方法是 sub-gradient descent, 就是每次疊代減小 learning rate ($\alpha \to \alpha_k$), \(x_{k+1} = x_k - \alpha_k \partial f(x_k)\) 雖然可行，但是收斂速度太慢。更好的方法是 proximal gradient descent.

光滑化有兩種方式：

  1. Conjugate function: 把不可微分的函數變成可微分共軛函數。

非光滑凸函數優化問題

  • 如果 $f(x)$ 是 $\beta$ smooth function, 直接用 GD 即可。只是要選一個適當的 $\alpha < \beta$.
  • 會有問題就是非光滑函數。我們就把這些函數分開 $f(x) + g(x)$ 其中 $f(x)$ 是光滑函數， $g(x)$ 是非光滑函數 (一般有限非光滑點)。

考慮一般非光滑問題:

\[\min_x f(x) + g(x)\]

其中 $f(x)$ 是 smooth function. $g(x)$ 包含非 smooth 點。最常見非光滑 (凸) 函數的就是 L1 norm 和 indicator function (0 in the constraint domain, $\infty$ otherwise), and L$\infty$ norm (max). L1 norm 很容易理解。Indicator function 常用於 constraint domain case. 就是把 constrain 轉換成 function.

Proximal Gradient Descent 結論

先說結論

$x_{k+1} = \arg \min_x {f(x_k) + \nabla f(x_k)(x-x_k) + \frac{1}{2\alpha_k}(x-x_k)^2 + g(x)} = prox_{\alpha_k g}(x_k - \alpha_k \nabla f(x_k)) $

PGD 可以視爲分成兩步

Step 1: 在光滑的 $f(x)$ 執行標準的 Gradient Descent: $z_k = x_k - \alpha_k \nabla f(x_k)$

Step 2: 在非光滑 (但 proximal friendly) 的 $g(x)$ 執行 proximal operation: $x_{k+1} = prox_{\alpha_k g} (z_k)$

下一個問題是什麼是 proximal operation? 可以參考 Stanford 的 paper [@boydProximalAlgorithms2013]

PGD 常見的説法

  • 假如 $g(x)$ 是 L1-norm, $f(x) + g(x)$ 稱爲 Lasso regularization. Proximal operation of L1 norm 對應一個 backward operation (見下圖紅線). 所以 PGD 有時稱爲 forward (GD, 下圖綠綫)-backward (L1 regularization, 下圖紅線) algorithm.

image-20230528090349216

  • 假如 $g(x)$ 是 indicator function (0 in the constraint domain, $\infty$ otherwise) 情況下, proximal operation 可以視爲 projection operation. 如果 GD 把 $z_k$ 移動出 constraint domain, proximal operation 再把 $z_k$ 投影回 constraint domain as $x_{k+1}$ .

Proximal Operator and Moreau Envelope Function

Proximal operator 和 Moreau envelope function 就是解決不可微分 (non-smooth) 的問題。

從值域 (Moreau envelope function)

先定義 Moreau envelope function 如下:

$M_{\gamma g}(x) = \inf_{z} \left{ g(z) + \frac{1}{2\gamma}(x-z)^2\right} \le g(x)$

$g(x) +\frac{1}{2\gamma}(x-x_k)^2 \ge g(x) \ge M_{\gamma g}(x)$.

  • Moreau envelope function $M_{\gamma g}(x)$ 永遠小於等於原來函數。是原來函數的光滑下界。如下圖虛線。
  • Morean function 的最小值等於原來函數的最小值。
  • 如果 $g(x)$ 是 convex function, Moreau function 也是 convex function
  • Moreau function 是否可微分? Yes! It’s always Frechet differentiable, with its gradient being 1-Lipschtz continuous. 也就是 smooth! 但並非 strongly convex!
  • 上式最左項是 $g(x)$ 加上一個正值的上界，也就是類似 Moreau 但沒有 $\inf$。如下圖的灰綫。

image-20230518210952149

從定義域 (Proximal Operator)

Proximal 是 operator $\R^n \to \R^n$, 而不是 function $\R^n \to \R$.

Proximal operator 的定義如下: \(\begin{aligned} \operatorname{prox}_{\gamma g}(x) & =\arg \min _z\left\{g(z)+\frac{1}{2 \gamma}(z-x)^2\right\} \end{aligned}\) 很難直接看出 proximal operator 的定義！特別是 operator 而不是 function.

Moreau envelope (or Moreau-Yosida regularization) function 和 proximal operator 有非常密切的關係，如下式。(How to prove?)

下式看起來非常像 gradient descent, 只是 $g(x) \to M_{\gamma g}(x)$, 就是下界函數。

如果沒有 gradient, 就換成 sub-differential. 不過 Moreau 應該 smooth, 所以 gradient 應該存在?
\(\begin{aligned} &\operatorname{prox}_{\gamma g}(x)=x-\gamma \nabla M_{\gamma g}(x) \\ & \operatorname{prox}_{\gamma g}(x)=x-\gamma \partial M_{\gamma g}(x)\end{aligned}\)

一個得到 prox operator 的方法就是從 Moreau envelope function 計算 GD 得出。一般不會這樣操作。

Example

例一: $f(z)$ 是光滑 function 假設 $f(z) \approx f(x) + (z-x) \nabla f + \frac{1}{2}(z-x)^2 \nabla^2 f +…$ \(\begin{aligned} \nabla f + (\nabla^2 f +\frac{1}{\gamma}) (z-x) = 0 \to z = prox_f(x) = x - \frac{\gamma}{1+\gamma \nabla^2 f} \nabla f \end{aligned}\)

  • 如果 $\gamma \nabla ^2 f \ll 1$, 也就是Hessian 遠小於 1/$\gamma$, Proximal operator 基本就化簡為 gradient descent.

例二: $\gamma \to +\infty$ (sanity check) \(\begin{aligned}\operatorname{prox}_{\gamma f}(x) & \approx \arg \min _z\left\{f(z)\right\} = x_{min}\end{aligned}\)

\[\begin{aligned}M_{\gamma f}(x) & \approx f_{min}\end{aligned}\]
  • 此時 prox operator 不論 input $x$ 是什麼，都輸出 $x_{min} \in \R^n$.

  • Moreau function 同樣不論 input $x$ 輸出 $ f_{min}$.

  • 因爲 Moreau function 是常數，其 gradient 為 0。$\gamma \to \infty$ 所以兩者抵消。
\[\begin{aligned}&\operatorname{prox}_{\gamma f}(x)=x-\gamma \nabla M_{f\gamma}(x) \approx x_{min}\end{aligned}\]

例三: $\gamma \to 0$ (sanity check) \(\begin{aligned}\operatorname{prox}_{\gamma f}(x) & \approx \arg \min _z\left\{\|z-x\|^2 \right\} = x\end{aligned}\)

\[\begin{aligned}M_{\gamma f}(x) & \approx f(x)\end{aligned}\]
  • 此時 prox operator 和 Moreau function 基本可以忽略。
\[\begin{aligned}&\operatorname{prox}_{\gamma f}(x)=x-\gamma \nabla M_{f\gamma}(x) \approx x\end{aligned}\]

Proximal operator 物理意義

控制 $\gamma$ from 0 to 無限大，可以看到 $prox_f(x)$ 從 $x$ 逼近 $x_{min}$. 在 $\gamma = 1$ 基本就是 $x$ 和 $x_{min}$ 之間！也就是 $x$ 被拉近到 $x_{min}$ 的位置！

也可以從這個公式看出：
\(\begin{aligned}&\operatorname{prox}_{\gamma f}(x)=x-\gamma \nabla M_{f\gamma}(x) \\& \operatorname{prox}_{\gamma f}(x)=x-\gamma \partial M_{\gamma f}(x)\end{aligned}\) $\gamma$ 越大，$x$ 就移動越靠近 $x_{min}$.

我們看實際的例子：

例四： $f(x) = \vert x \vert$

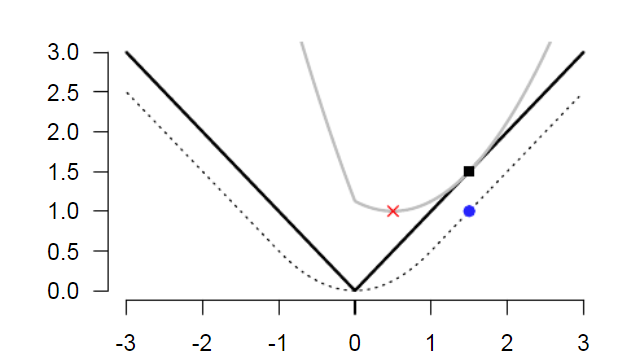
  • $f(x)$ 如下圖實心黑線。

  • $f(x)$ 的 Moreau function $M_f(x)$ 如下。物理意義是 Huber function，是一個下界可微分函數。

\[M_{\gamma f}(x)=\inf _z\left\{|z|+\frac{1}{2 \gamma}(z-x)^2\right\}= \begin{cases}\frac{1}{2 \gamma} x^2, & |x| \leq \gamma, \\ |x|-\frac{\gamma}{2}, & |x|>\gamma .\end{cases}\]

  • 假設 $\gamma = 1$, Moreau function 就是下圖虛線。

  • 灰色的實線對應 $\vert x \vert + (1/2)(x-x_0)^2$ for $x_0=1.5$. 其 minimum 是紅點位置。

    • 對應的 $x=0.5$ 就是 1-D proximal operator output: $prox_f(1.5)=0.5$
    • 對應的 $y = 1$ 就是 Moreau function: $M_f(1.5) = 1$

image-20230518210952149

以上例 $f(x) = \vert x \vert$ , L1-norm 來看

  • $prox_f(1.5) = 1.5 - 1 = 0.5$!

  • $prox_f(1) = 1 - 1 = 0$

  • $prox_f(0.5) = 0.5 - 0.5 = 0$

  • $prox_f(0) = 0 - 0 = 0$ (minimum!) \(prox_{\gamma f}(x) = x - \gamma \nabla M_{\gamma f}= \begin{cases} x-\gamma, & x > \gamma, \\ 0, & \vert x \vert \le \gamma , \\ x+\gamma, & x < -\gamma .\end{cases}\)

  • 如果用 $x_{k+1} = prox(x_k)$ 最後可以疊代出 $x_{i} \to 0$, 也就是 $x_{min}$ 得到 $f(x)$ 的極小值。

例五

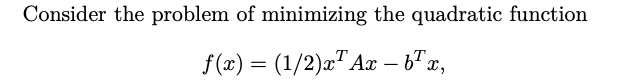
image-20230511212515508

Where A is semidefinite.

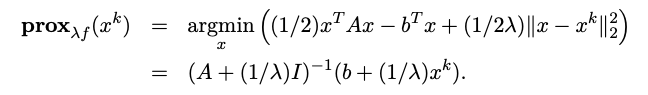
image-20230511212612101

image-20230511212906941

Where $\epsilon = 1/\lambda$

主角 - Proximal Gradient Descent

臨近類方法是用於處理目標函數中含有非光滑項，並且該非光滑項是“臨近友好的”，意思就是它的臨近算子 (proximal operator) 是容易計算的，或是有閉式解。首先考慮一般問題 \(\min_x f(x) + g(x)\)

這裡的 $f(x)$ 是光滑的，而 $g(x)$ 為非光滑的，通常為某種正則函數，或是 (非光滑) L1-norm 之類，當然也有可能為某個約束集 (constraint set) 的指示函數 (indicator)，這個時候就變成約束優化 (constrained optimization) 問題了。

PGD 的疊代法：

$x_{k+1} = \arg \min_x {f(x_k) + \nabla f(x_k)(x-x_k) + \frac{1}{2\alpha_k}(x-x_k)^2 + g(x)} = prox_{\alpha_k g}(x_k - \alpha_k \nabla f(x_k)) $

此處 $\alpha_k$ 是基於光滑函數 $f(x)$，可以收斂比較快。

Proximal Gradient Descent 可視爲分為兩步：

Step 1: 在光滑的 $f(x)$ 執行標準的 Gradient Descent: $z_k = x_k - \alpha_k \nabla f(x_k)$

Step 2: 在非光滑 (但 proximal friendly) 的 $g(x)$ 執行 proximal operation: $x_{k+1} = prox_{\alpha_k g} (z_k) = z_k - \alpha_k \nabla M_{\alpha_k g}$

當不可微的凸函數的形式為 $g(\boldsymbol{w})=|\boldsymbol{w}|_1$ 時，則對應的軟閾值函數為 \(\left[\mathcal{S}_t(\boldsymbol{w})\right]_i= \begin{cases}w_i-t, & \text { if } w_i>t \\ 0, & \text { if }\left|w_i\right| \leq t \\ w_i+t, & \text { if } w_i<-t\end{cases}\) 如果 $g$ 是 L1-norm (Lasso) with parameter $\lambda$,
\(\begin{aligned}\boldsymbol{w}^k & =\operatorname{prox}_{\alpha g(\cdot)}\left(\boldsymbol{w}^{k-1}-\alpha \nabla f\left(\boldsymbol{w}^{k-1}\right)\right) \\& =\mathcal{S}_{\alpha}\left(\boldsymbol{w}^{k-1}-\alpha \nabla f\left(\boldsymbol{w}^{k-1}\right)\right)\end{aligned}\) 其中，變數上標的 $k$ 表示當前疊代次數。

Lasso 的 sparsity (係數為 0) 的特性也可以從此看出！！

Lasso 其實也即是 quantization, 只是 apply 在 0 附件 only!

  • 假如 $g(x)$ 是 L1-norm, $f(x) + g(x)$ 稱爲 Lasso regularization. Proximal operation of L1 norm 對應一個 backward operation (見下圖紅線). 所以 PGD 有時稱爲 forward (GD, 下圖綠綫)-backward (L1 regularization, 下圖紅線) algorithm.

image-20230528090349216

  • 假如 $g(x)$ 是 indicator function (0 in the constraint domain, $\infty$ otherwise) 情況下, proximal operation 可以視爲 projection operation. 如果 GD 把 $z_k$ 移動出 constraint domain, proximal operation 再把 $z_k$ 投影回 constraint domain as $x_{k+1}$ .

PGD Summary

如果 $L(x) = f(x) + g(x)$，$f(x)$ 是光滑函數；$g(x)$ 是非光滑函數但是 proximal operation friendly.

  • 如果 $f(x)=0$, 直接用 $x_{k+1} = prox_{\lambda g}(x_k)$

  • 標準的 PGD:

image-20230515221508382

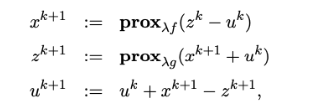
  • 還有 ADMM image-20230530224246742 image-20230520103700590

  • 特例就是 x - z = or x = z
  • Linearized ADMM
    • $\min f(x) + g(Ax)$

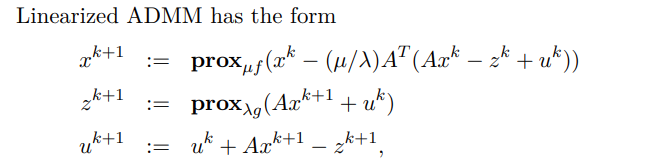
image-20230618220627878

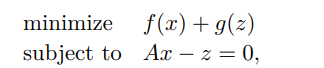
image-20230618220708081

PGD 三種特例

  • $g = 0 \to $ PGD = gradient descent (trivail)
  • $g = I_C \to$ 如果 $g$ 是 indicator function, PGD = projected gradient descent
  • $f = 0 \to$ Proximal minimization algorithm (一般沒有太大用途)

Proximal Minimization Algorithm

$x^* = prox_{\lambda f}(x^) \text{ iff } x^$ is the minimum. \(\begin{aligned}\operatorname{prox}_{\gamma g}(x) & =\arg \min _z\left\{g(z)+\frac{1}{2 \gamma}\|z-x\|_2^2\right\}\end{aligned}\)

假設 $f(x) = 0$

$x_{k+1} = prox_{\lambda g}(x_k)$

最後會收斂到最小值，只要 $g$ 是 contracting function.

Conjugate Function

在引入 conjugate function 後，事情變得更有趣！

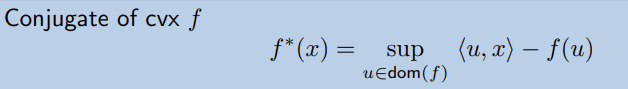
image-20230520131908241

主要用到的就是共軛函數的性質，首先，對於一個正常閉凸函數，可以表示成：

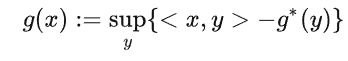
image-20230528223106806

這裡 $g^$ 是一個凸函數，根據 Conjugate Correspondence Theorem，我們知道“強凸函數”的共軛是一個光滑函數。上式中， $g$ 表達成了 $g^$ 的共軛函數，那麼我們是不是可以通過加個二次正則，使得 $g^*$ 加上這個函數變成強凸函數，這樣就起到了光滑的作用了。利用這個定理，我們很容易得到下面這個光滑化函數

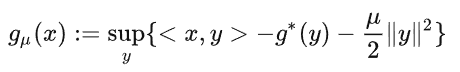
image-20230528223829095

非常重要，可以證明: \(g_u(x) = M_{\mu g}(x)\) [@dengSmoothFramework2020]

$M_{\mu g}(x) = \inf_{z} \left{ g(z) + \frac{1}{2\mu}(x-z)^2\right} = g_{\mu}(x) \le g(x)$

Obviously, 如果 $\mu \to 0\Rightarrow g_{\mu}(x) \to g(x)$

也就是把非光滑的 $g(x)$ 可以轉換成光滑而且強凸函數的 conjugate of 加料 conjugate function $g_{\mu}(x)$; 剛好這個 conjugate of 加料 conjugate function 正好就是 Moreau envelope function!

Moreau Decomposition

可以證明 Moreau Decomposition

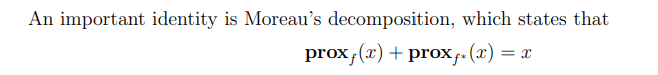
image-20230520131956150

我們直接看例子：$g(x) = \vert x \vert$ 也就是 L1 norm.

L1 norm 對應的 conjugate function 是 indicator function： $g^*(x) = I_C(x)$ 如下.

此處 $C = [-1, 1]$ in $\R^1$ or $C = |x|_{\infty} \le 1$ in $\R^n$

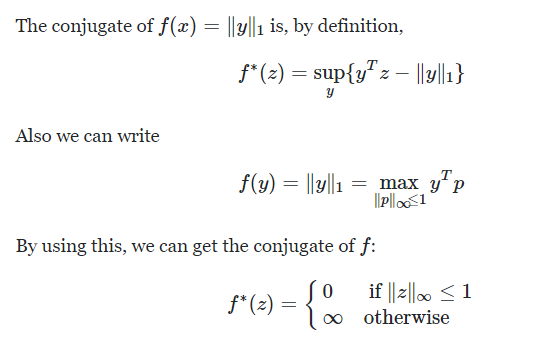
image-20230603211947972

L1 norm $g(x)$ 對應的 proximal function 是 soft-threshold function 如下。 \(prox_g(x)= \begin{cases}x-1, & \text { if } x>1 \\ 0, & \text { if }\left|x\right| \leq 1 \\ x+1, & \text { if } x<-1\end{cases}\)

​

Indicator function $g^*(x)$ 對應的 proximal function 是 projector to $C$ 如下。 \(prox_{g^*}(x)= \begin{cases}1, & \text { if } x>1 \\ x, & \text { if }\left|x\right| \leq 1 \\ -1, & \text { if } x<-1\end{cases}\)

可以確認：Moreau decomposition: $x = prox_{g}(x) + prox_{g^*} (x)$

Q&A 但因爲 \(\begin{aligned}&\operatorname{prox}_{\gamma g}(x)=x-\gamma \nabla M_{g\gamma}(x)\end{aligned}\) 所以 $\nabla M_g(x) = prox_{g^*}(x)$? YES!

$M_g(x)$ 是 Huber function, 是 $g(x) = \vert x \vert$ 的下界光滑函數。 \(M_{g}(x)=\inf _z\left\{|z|+\frac{1}{2 }(z-x)^2\right\}= \begin{cases}\frac{1}{2} x^2, & |x| \leq 1, \\ |x|-\frac{1}{2}, & |x|>1 .\end{cases}\)

\[\nabla M_{g}(x)=\begin{cases}1, & \text { if } x>1 \\ x, & \text { if }\left|x\right| \leq 1 \\ -1, & \text { if } x<-1\end{cases}\]

Performance Comparison

Convergence Rate

一般的 $f(x) + g(x)$ 非光滑函數。以 L1 norm (Lasso) 爲例。

如果用 sub-gradient, $O(1/\epsilon^2)$

如果用 proximal gradient descent, $O(1/\epsilon)$

如果加上 accelerated PGD (or momentum PGD), $O(1/\sqrt{\epsilon})$

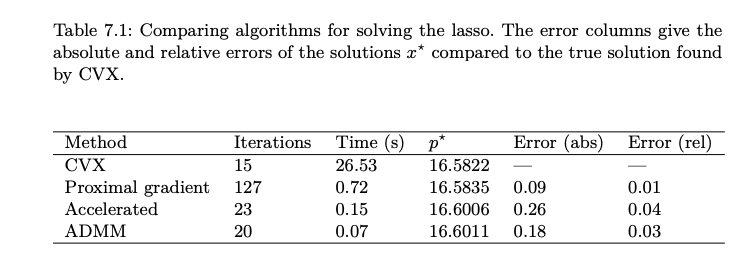
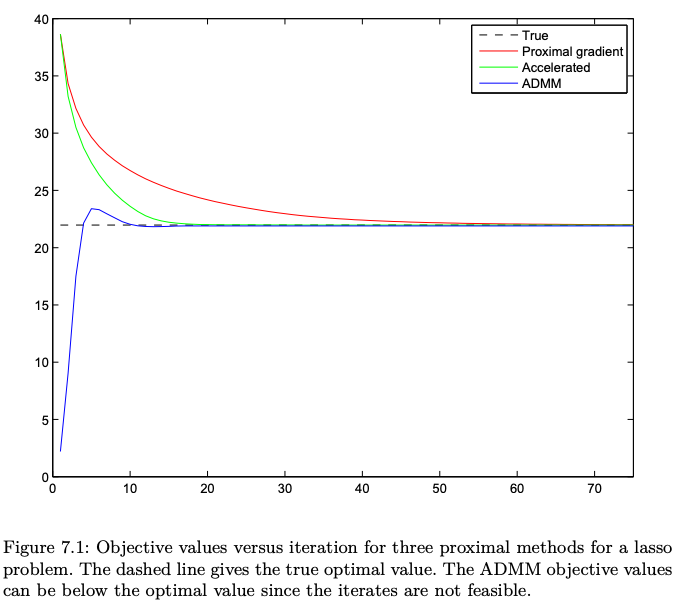
Lasso of Quadratic

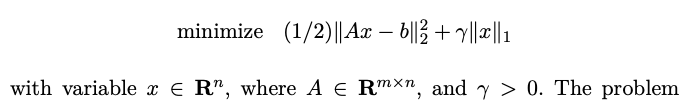
image-20230511214346967

CVX: 2nd order method : fast and accurate but expensive

Proximal gradient: 1st order, slow

Accelerated Proximal: 1st order, fast

ADMM: 1st order, fastest

image-20230511214130919

image-20230511214459012

Appendix A

We can rearrange terms to express $M_{\gamma f}(x)$ in the following form: \(\begin{aligned} & M_{\gamma f}(x)=\frac{1}{2 \gamma}\|x\|^2-\frac{1}{\gamma} \sup _y\left\{x^T y-\gamma f(y)-\frac{1}{2}\|y\|^2\right\} \\ &=\frac{1}{2 \gamma}\|x\|^2-\frac{1}{\gamma}\left(\gamma f+\frac{1}{2}\|\cdot\|^2\right)^*(x) \\ & \therefore \nabla M_{\gamma f}(x)=\frac{x}{\gamma}-\frac{1}{\gamma} \underset{y}{\operatorname{argmax}}\left\{x^T y-\gamma f(y)-\frac{1}{2}\|y\|^2\right\} \\ &=\frac{1}{\gamma}\left(x-\operatorname{prox}_{\gamma f}(x)\right) \\ & \Rightarrow \operatorname{prox}_{\gamma f}(x)=x-\gamma \nabla M_{\gamma f}(x) \\ & \operatorname{prox}_{\gamma f}(x)=x-\gamma \partial M_{\gamma f}(x), \\ & M_{\gamma f}(x)= \min _y\left\{f(y)+\frac{1}{2 \gamma}\|x-y\|^2\right\} \\ &= \min _y\left\{f(y)+\frac{1}{2 \gamma}\|z\|^2\right\} \text { such that } x-y=z \end{aligned}\) (Note the substitution trick here is a very useful technique.) The Lagrangian and the Lagrange dual function are given by \(\begin{aligned} \mathcal{L}(y, z, \lambda) & =f(y)+\frac{1}{2 \gamma}\|z\|^2+\lambda^T(x-y-z) \\ & =\left[f(y)-\lambda^T y\right]+\left[\frac{1}{2 \gamma}\|z\|^2-\lambda^T z\right]+\lambda^T x \\ g(\lambda) & =\inf _{y, z} \mathcal{L}(y, z, \lambda) \\ & =\inf _y\left\{f(y)-\lambda^T y\right\}-\frac{\gamma}{2}\|\lambda\|^2+\lambda^T x \\ & =-f^*(\lambda)-\frac{\gamma}{2}\|\lambda\|^2+\lambda^T x \\ f_\gamma(x)=\sup _\lambda g(\lambda) & =\sup _\lambda\left\{-f^*(\lambda)-\frac{\gamma}{2}\|\lambda\|^2+\lambda^T x\right\} \\ & =\left(f^*+\frac{\gamma}{2}\|\cdot\|^2\right)^*(x) \end{aligned}\)

Appendix B : 光滑算法框架

這裡主要用到的就是共軛函數的性質，首先，對於一個正常閉凸函數，可以表示成：

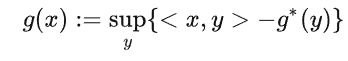
image-20230528223106806

這裡 $g^$ 是一個凸函數，根據 Conjugate Correspondence Theorem，我們知道“強凸函數”的共軛是一個光滑函數。上式中， $g$ 表達成了 $g^$ 的共軛函數，那麼我們是不是可以通過加個二次正則，使得 $g^*$ 加上這個函數變成強凸函數，這樣就起到了光滑的作用了。利用這個定理，我們很容易得到下面這個光滑化函數

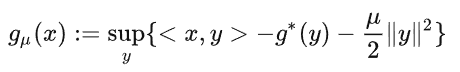
image-20230528223829095

非常重要，可以證明: \(g_u(x) = M_{\mu g}(x)\) [@dengSmoothFramework2020]

也就是光滑函數可以是 Moreau envelope function 或是 conjugate function with L2 norm!

知道了原理，只要後面是個強凸項就可以了，所以可以得到更一般的形式：

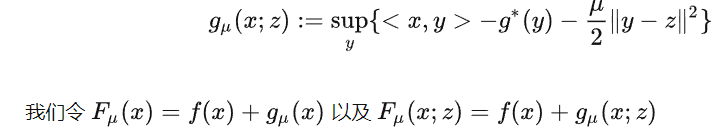
image-20230528224020166

框架一

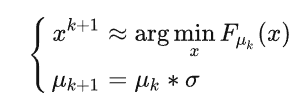
image-20230528230927285

大概思想就是，最開始光滑參數 $\mu_k$ 比較大，也就是很光滑。後面 $\mu_k$ 慢慢減小趨于零。每次我們近似求解光滑化問題，比如：

  • 滿足一定的精度，比如 $| \nabla F_{u_k}(x^{k+1})| \le \epsilon_k$
  • 執行固定的梯度疊代就跳出
  • 只執行一次梯度疊代，即 $x^{k+1} = x^k - \alpha_k \nabla F_{u_k}(x_k)$
  • 求到精確解。

這和 sub-gradient 好像一樣?

既然是框架，就要做的general一點，我們考慮（4）式中的光滑化函數

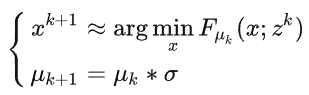
image-20230528232648325

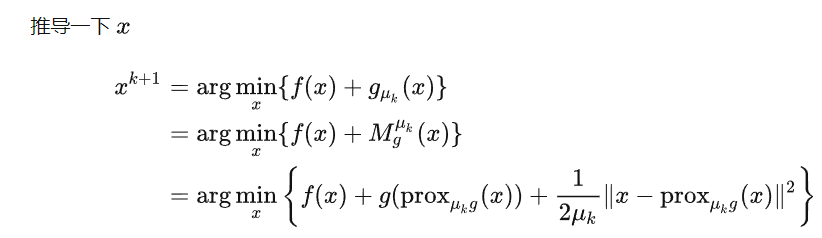
image-20230528232849811

例子一: g(x) 是 indicator function. Prox_g 就是 projection function. Pc(x)

所以 g( prox(x)) = 0!!! 因爲 g(x) 是 indicator, 而且 prox(x) project x 回到 g 的 domain. 所以 g(prox())

image-20230603164424018

image-20230528232940372

Appendix C: PGD 證明

對於優化問題 $\min _{\boldsymbol{w}} f(\boldsymbol{w})+g(\boldsymbol{w})$ ，$f$ 是 smooth, $g$ 是 non-smooth 變數 $\boldsymbol{w}$ 的疊代遞推公式為 \(\begin{aligned} \boldsymbol{w}^k & =\operatorname{prox}_{\alpha g(\cdot)}\left(\boldsymbol{w}^{k-1}-\alpha \nabla f\left(\boldsymbol{w}^{k-1}\right)\right) \\ \end{aligned}\)

疊代遞推公式證明過程

\[\begin{aligned} \boldsymbol{w}^k & =\operatorname{prox}_{\alpha g(\cdot)}\left(\boldsymbol{w}^{k-1}-\alpha \nabla f\left(\boldsymbol{w}^{k-1}\right)\right) \\ & =\arg \min _z g(\boldsymbol{z})+\frac{1}{2 \alpha}\left\|\boldsymbol{z}-\left(\boldsymbol{w}^{k-1}-\alpha \nabla f\left(\boldsymbol{w}^{k-1}\right)\right)\right\|_2^2 \\ & =\arg \min _{\boldsymbol{z}} g(\boldsymbol{z})+\frac{\alpha}{2}\left\|\nabla f\left(\boldsymbol{w}^{k-1}\right)\right\|_2^2+\nabla f\left(\boldsymbol{w}^{k-1}\right)^{\top}\left(\boldsymbol{z}-\boldsymbol{w}^{k-1}\right)+\frac{1}{2 \alpha}\left\|\boldsymbol{z}-\boldsymbol{w}^{k-1}\right\|_2^2 \\ & =\arg \min _{\boldsymbol{z}} g(\boldsymbol{z})+f\left(\boldsymbol{w}^{k-1}\right)+\nabla f\left(\boldsymbol{w}^{k-1}\right)^{\top}\left(\boldsymbol{z}-\boldsymbol{w}^{k-1}\right)+\frac{1}{2 \alpha}\left\|\boldsymbol{z}-\boldsymbol{w}^{k-1}\right\|_2^2 \\ & \approx \arg \min _{\boldsymbol{z}} f(\boldsymbol{z})+g(\boldsymbol{z}) \end{aligned}\]

注意: 由於公式第三行中的 $\frac{\alpha}{2}\left|\nabla f\left(\boldsymbol{w}^{k-1}\right)\right|_2^2$ 和第四行中的 $f\left(\boldsymbol{w}^{k-1}\right)$ 均與決策變數 $\boldsymbol{z}$ 無關，因 此公式第三行等於公式第四行。

Reference

[@boydProximalAlgorithms2013]