Optimization - Accelerate Gradient Descent

Source

1. https://www.youtube.com/watch?v=ht-gvPFsYh4&ab_channel=HanDean CMU youtube video

2. https://distill.pub/2017/momentum/ Accelerated GD

Introduction

Gradient descent (GD) 在一般的凸函數的收斂速度是 $O(1/\epsilon)$。在非光滑凸函數只能用 Sub-gradient method, 收斂速度更慢，只有 $O(1/\epsilon^2)$!

Proximal gradient descent (PGD) 可以解決非光滑凸函數收斂慢的問題。如果非光滑凸函數的 proximal operator 很容易計算，例如 L1 norm, indicator function 等等，PGD 基本就和 GD 一樣，可以在 $O(1/\epsilon)$ 收斂，而且是非光滑凸函數！

下一個問題是否能更快？YES! 這就是 accelerated gradient descent, 或是 accelerated proximal gradient descent.

我們先説結論：accelerated gradient descent 對於光滑凸函數的收斂速度是 $O(1/\sqrt{\epsilon})$。accelerated proximal gradient descent 對於非光滑凸函數的收斂速度也是 $O(1/\sqrt{\epsilon})$。

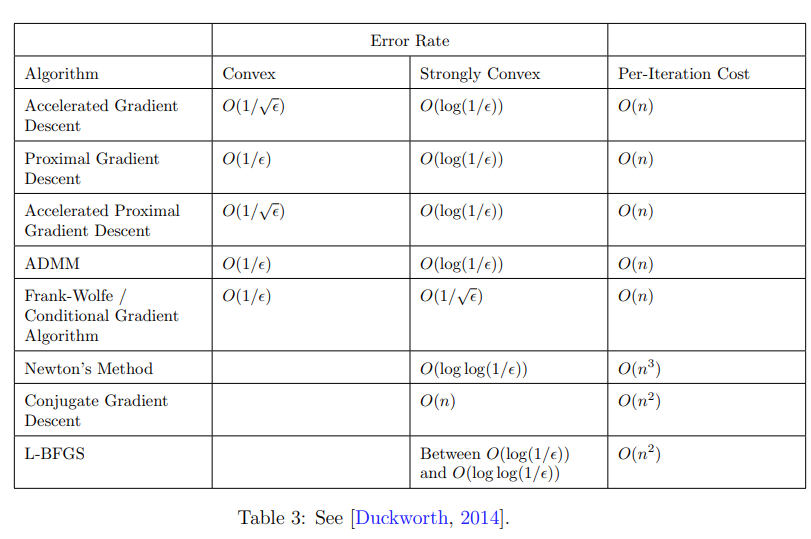
Accelerated Gradient Descent

Gradient descent 物理上常常和小球滑到山谷的最低點類比。我們看一下 GD 的公式：

$x_{k+1} = x_k - \alpha \nabla f(x_k)$

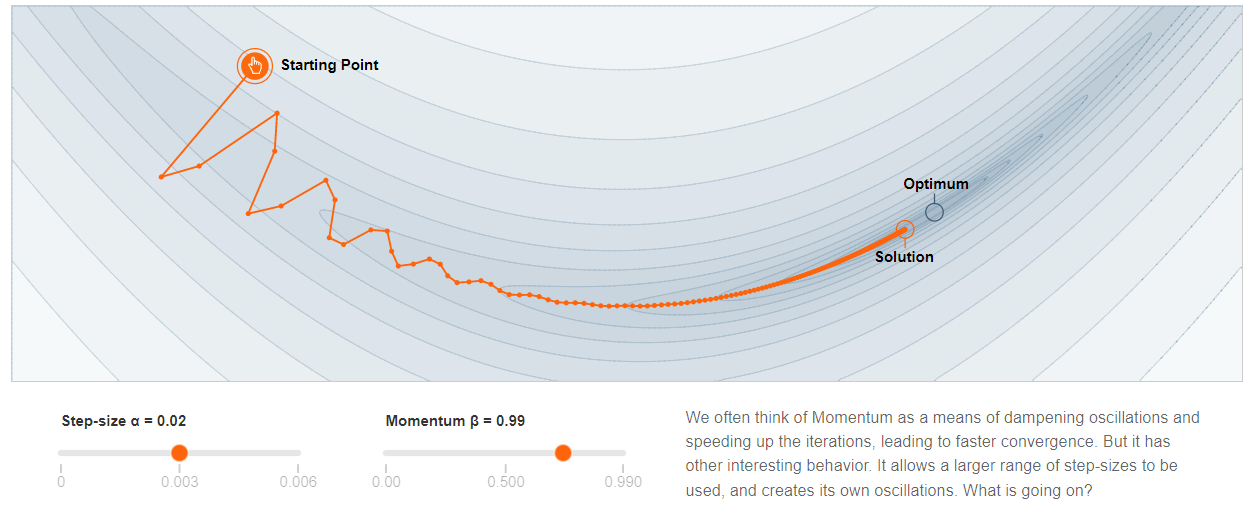
假設每次迭代的時間都是 1 秒，$x_{k+1} - x_k$ 就是速度，$\nabla f(x)$ 相當於 (重) 力。力和速度而非加速度成正比，物理上相當於摩擦力。可以想象整個山谷都浸在水裏，水的阻力就是摩擦力，$\alpha$ 就是摩擦力的倒數。$\alpha$ 愈大，摩擦力愈小，容易 overshoot 甚至發散。反之 $\alpha$ 愈小，摩擦力愈大，收斂的速度愈慢。

Accelerated gradient descent 的公式：

$v_{k+1} = \beta v_k - \alpha\nabla f(x_k)$

$x_{k+1} = x_k + v_{k+1}$

$z_k$ 稱爲 momentum 項。因爲如果 $\beta = 1 \to \nabla f = z_{k+1} - z_k$ 類似 F = d(mv)/dt, 也就是 momentum.

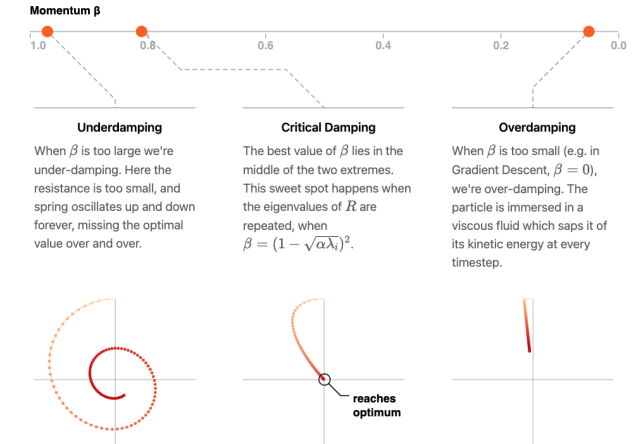
$\beta=0$ 就和 GD 一樣 (over-damped)。 $\beta$ 愈接近 1 代表 momentum 愈大 (under-damped)。

此時 $\alpha$ 因爲是位置和 momentum 的比例，相當於質量而不是摩擦力的倒數。

• 在 high curvature direction, 前後 gradient 方向相反而會互相抵消，因此是 damped oscillation. $\beta$ 接近 1, 代表抵消效果越好。
• 在 low curvature direction, 前後 gradient 方向相同互相加强。可以很快收斂。 如下圖。

Quadratic Function

我們用 (矩陣) 二次式爲例。雖然是簡單的例子，但有物理意義。 \(f(w)=\frac{1}{2} w^T A w-b^T w, \quad w \in \mathbf{R}^n\) 此處假設 $A$ 是對稱而且可逆 (full rank) 矩 (方) 陣。因此 optimal solution $w^{\star}$ 是當 \(w^{\star}=A^{-1} b\) (Yes!) 如果要 convex, 是否需要所以 eigenvalues 都是正值？ positive semi-definite?, i.e. $A \succeq 0$, 加上 invertible 所以 $A \succ 0$

Gradient Descent

因爲 $\nabla f(w)=A w-b$, GD 的迭代公式如下 \(w^{k+1}=w^k-\alpha\left(A w^k-b\right)\) 對於對稱的矩陣 $A$ 做 eigenvalue decomposition \(A=Q \operatorname{diag}\left(\lambda_1, \ldots, \lambda_n\right) Q^T, \quad Q=\left[q_1, \ldots, q_n\right]\) 另外根據習慣， $\lambda_i$ 從小排到大： $\lambda_1$ (最小) to biggest $\lambda_n$ (最大)。$Q$ 是 (幺) 正交矩陣 (orthonormal) , $q_i$ 對應新的正交基底，$\lambda_i$ 是新的 scaling factor。

再來做一個基底變換 ($w \to x$) 並扣除 bias, $x^k=Q^T\left(w^k-w^{\star}\right)$, 可以讓 GD 迭代變成每個基底 separable! 而更有物理意義！ \(w^{k+1}=w^k-\alpha\left(A w^k-b\right) \\ Q^T(w^{k+1} - w^*)= Q^T(w^k - w^*) -\alpha Q^T\left(A w^k-b\right) \\ x^{k+1} = x^k - \alpha Q^T A (w^k - A^{-1} b) \\ x^{k+1} = x^k - \alpha Q^T Q D Q^T (w^k - A^{-1} b) = x^k - \alpha D x^k\) 再來拆開每個坐標軸！ \(\begin{aligned} x_i^{k+1} & =x_i^k-\alpha \lambda_i x_i^k \\ & =\left(1-\alpha \lambda_i\right) x_i^k=\left(1-\alpha \lambda_i\right)^{k+1} x_i^0 \end{aligned}\) 其中 $x_i$ 對應 $q_i$ 坐標軸。

• 此時我們可以把 $\R^n$ 的優化問題變成 $n$ 個 $\R^1$ 的優化問題！

• 每個坐標軸 $q_i$ 從初始距離 $x_i^0$ 呈幾何數列 (公比 $1-\alpha \lambda_i$) 收斂到 0.

• 收斂的條件是 $\vert 1-\alpha_i \lambda_i \vert < 1$. 收斂最慢的坐標軸就決定最終的收斂速度，也就是 bottleneck.

回到原始的坐標系 $w$, 變回 $\R^n$ ($q_1, q_2, …, q_n \in \R^n$), 可以得到 GD 的 close form in $\R^n$. 不過沒有上式有物理意義！ \(w^k-w^{\star}=Q x^k=\sum_i^n x_i^0\left(1-\alpha \lambda_i\right)^k q_i\)

最佳步長 $\alpha$

前面分析提供直接的 guidance 如何選取步長 $\alpha$.

• 收斂的條件是 $\left

  1-\alpha \lambda_i\right

  < 1$, 也就是 $0<\alpha \lambda_i<2$, 似乎可以推導出 $ \to 0<\alpha < 2/\lambda_i$ 。 Yes! 因爲 convex 要求所有 $\lambda_i$ 是正數！不過假設所有 eigenvalues 都是正值而且 $\lambda_n$ 是最大 eigenvalue，$0 < \alpha < 2/\lambda_n$

• 整體收斂速度是由上式最慢的 error term 決定，也就是最接近 +1 或是 -1. 因爲 $\lambda_i$ 從小排到大： $\lambda_1$ (最小，可爲負值) to biggest $\lambda_n$ (最大)。直觀上收斂的 rate 只由最大或最小的 eigenvalue 決定！ $\lambda_1$ or $\lambda_n$ :

\(\begin{aligned} \operatorname{rate}(\alpha) & =\max _i\left|1-\alpha \lambda_i\right| \\ & =\max \left\{\left|1-\alpha \lambda_1\right|,\left|1-\alpha \lambda_n\right|\right\} \end{aligned}\) 我們現在要選擇 $\alpha$ to minimize rate($\alpha$) , 就是上式！

• 如果 $\lambda_1 = \lambda_n$ 代表所有的 eigenvalues 都一樣。這是 trivial case, 只要選 $\alpha = 1/\lambda_1 = 1/\lambda_n \to \min \operatorname{rate}(\alpha) = 0$ 一步到位。
• 如果 $\lambda_1 \ne \lambda_n$. 一個自然 (但非最佳) 的選擇是 $\alpha = 1/\lambda_n \to$ $\operatorname{rate}(\alpha) = 1-\lambda_1 / \lambda_n < 1$
• 最佳的解是讓 $1-\alpha \lambda_1$ 和 $1-\alpha \lambda_n$ 在 0 兩側相等！
  • $1-\alpha \lambda_1 = -(1-\alpha\lambda_n ) \to \text { optimal } \alpha=\underset{\alpha}{\operatorname{argmin}} \operatorname{rate}(\alpha) = \frac{2}{\lambda_1 + \lambda_n}$
  • $\text { optimal rate }=\min _\alpha \operatorname{rate}(\alpha)=\frac{\lambda_n / \lambda_1-1}{\lambda_n / \lambda_1+1}$
  • 可以看一下比較: $\lambda_n = 5 \lambda_1$, 自然解的 rate = 1 - 1/5 = 4/5; 最佳解 = (5-1)/(5+1) = 4/6 更小!

In summary \(\begin{aligned} & \text { optimal } \alpha=\underset{\alpha}{\operatorname{argmin}} \operatorname{rate}(\alpha)=\frac{2}{\lambda_1+\lambda_n} \\ & \text { optimal rate }= \gamma_{GD} = \min _\alpha \operatorname{rate}(\alpha)=\frac{\lambda_n / \lambda_1-1}{\lambda_n / \lambda_1+1} = \frac{\kappa -1}{\kappa+1} \end{aligned}\) Notice the ratio $\lambda_n / \lambda_1$ determines the convergence rate of the problem. In fact, this ratio appears often enough that we give it a name, and a symbol - the condition number. \(\text { condition number }:=\kappa:=\frac{\lambda_n}{\lambda_1}\) Question: 爲什麽不讓 $\alpha$ 從純量 (scalar) 變成向量? 就是每個 $q_i, \lambda_i$ 都有自己的 $\alpha_i$?

Decompose Error

\[\epsilon = f(w^k)- f(w^{\star}) = \sum_i^n \left(1-\alpha \lambda_i\right)^{2k} \lambda_i [x_i^0]^2\]

Optimal Rate and Error Converge Rate

有兩種方式評價不同算法的效能: (1) optimal rate; (2) Error Converge Rate.

Optimal rate 就是等比級數的公比 $\gamma = \min_{\alpha} \vert 1-\alpha \lambda_i \vert = \frac{\kappa-1}{\kappa +1} < 1$ ，越小收斂越快

Error Converge Rate 則是 $\epsilon$ 和 $k$ 的關係 $k = \frac{\log \epsilon + c}{2 \log \gamma} \propto O(\log (\frac{1}{\epsilon})/\log(\frac{1}{\gamma}))$ ，越小收斂越快

• 對於 strong convex function, 才會有等比數列收斂的公比 $\gamma$ and $\log \epsilon$
• 如果是一般 convex function, 一般用 Error Converge Rate 而不用 $\gamma$

Gradient Descent 收斂速度

• $\kappa \ge 1$

• Optimal rate = $\gamma_{GD} = \frac{\kappa-1}{\kappa+1}$ 越小越好收斂越快

• 最容易的例子是 $\kappa=1$, 可以很快收斂。如果 $\kappa \gg 1$, 稱爲 ill-condition, GD 只能讓 $\alpha$ 變小才能收斂。這會導致收斂速度變慢。

Accelerated (Momentum) Gradient Descent

接下來我們研究 accelerated (momentum) GD 如下：

\(\begin{aligned} z^{k+1} & =\beta z^k+\nabla f\left(w^k\right) \\ w^{k+1} & =w^k-\alpha z^{k+1} \end{aligned}\) 二次式, $\nabla f\left(w^k\right)=A w^k-b$, 的迭代公式如下： \(\begin{aligned} z^{k+1} & =\beta z^k+\left(A w^k-b\right) \\ w^{k+1} & =w^k-\alpha z^{k+1} . \end{aligned}\) 同樣我們可以做基底變換： $x^k=Q\left(w^k-w^{\star}\right)$ and $y^k=Q z^k$, 得到每個基底 separable 的迭代!
\(\begin{aligned} & y_i^{k+1}=\beta y_i^k+\lambda_i x_i^k \\ & x_i^{k+1}=x_i^k-\alpha y_i^{k+1} . \end{aligned}\) 注意上式每一個基底都是獨立分離的！(雖然 $x_i^k$ and $y_i^k$ are coupled). 我們把上式改寫成如下： \(\left(\begin{array}{c} y_i^k \\ x_i^k \end{array}\right)=R^k\left(\begin{array}{c} y_i^0 \\ x_i^0 \end{array}\right) \quad R=\left(\begin{array}{cc} \beta & \lambda_i \\ -\alpha \beta & 1-\alpha \lambda_i \end{array}\right)\) 非常有趣，accelerated GD 的物理意義是把原來 1D 的 exponential decay (等比公式)，轉換成 2D (2x2 矩陣) damped oscillation!!

• 假設 2x2 矩陣 $R$ 的 eigenvalues 是 $\sigma_1$ 和 $\sigma_2$. $\vert \sigma_1 \vert, \vert \sigma_2 \vert < 1$. 這樣才可以保證收斂！

• 注意 $\sigma_1$ 和 $\sigma_2$ 不一定是實數。如果要收斂快，最好是 damped oscillation！如此 $\sigma_1, \sigma_2$ 就會是 (共軛) 複數。

• 可以得到下列公式 for $R^k$：

\(R^k=\left\{\begin{array}{ll} \sigma_1^k R_1-\sigma_2^k R_2 & \sigma_1 \neq \sigma_2 \\ \sigma_1^k\left(k R / \sigma_1-(k-1) I\right) & \sigma_1=\sigma_2 \end{array}, \quad R_j=\frac{R-\sigma_j I}{\sigma_1-\sigma_2}\right.\)

Optimal parameters $\alpha, \beta$

我們同樣可以優化 $\alpha$ and $\beta$ 得到最快的 global convergence rate。結果如下： \(\alpha=\left(\frac{2}{\sqrt{\lambda_1}+\sqrt{\lambda_n}}\right)^2 \quad \beta=\left(\frac{\sqrt{\lambda_n}-\sqrt{\lambda_1}}{\sqrt{\lambda_n}+\sqrt{\lambda_1}}\right)^2\) 將 $\alpha, \beta$ 帶入 $R$ 矩陣，可以得到 \(\gamma_{AGD} = \frac{\sqrt{\kappa}-1}{\sqrt{\kappa}+1} \begin{aligned} \end{aligned}\)

• $\kappa \ge 1$ and $0 \le \beta < 1$

• AGD optimal rate $\gamma_{AGD} = \frac{\sqrt{\kappa}-1}{\sqrt{\kappa}+1}$ 越小越好收斂越快。在 $\kappa \gg 1$ , 也就是 ill-condition $\gamma_{AGD} \ll \gamma_{GD} < 1$, AGD 收斂比 GD 快得多。

• Error Converge Rate: $O(\log (\frac{1}{\epsilon})/\log(\frac{1}{\gamma_{AGD}})) < O(\log (\frac{1}{\epsilon})/\log(\frac{1}{\gamma_{GD}})) $ 因爲有 log 函數，其實好像沒有差太多。

Proximal Gradient Descent (PGD)

雖然沒有人直接用 PGD 於二次式，但看一下結果還是非常有物理意義。

From [@boydProximalAlgorithms2013]

首先二次式 \(f(w)=\frac{1}{2} w^T A w-b^T w, \quad w \in \mathbf{R}^n\)

接著

\[\begin{aligned} \operatorname{prox}_{\alpha f}\left(w^k\right)& =\underset{w}{\operatorname{argmin}}\left((1 / 2) w^T A w-b^T w+\frac{1}{2 \alpha}\left\|w-w^k\right\|_2^2\right) \\ & =(A+(1 / \alpha) I)^{-1}\left(b+(1 / \alpha) w^k\right) \end{aligned}\]

利用 proximal iterative algorithm

\[\begin{aligned} w^{k+1} &=(A+(1 / \alpha) I)^{-1}\left(b+(1 / \alpha) w^k\right), \\ &=w^k+(A+\epsilon I)^{-1}\left(b-A w^k\right), \end{aligned}\]

where $\epsilon = 1/\alpha$

利用 $A=Q \operatorname{diag}\left(\lambda_1, \ldots, \lambda_n\right) Q^T, \quad Q=\left[q_1, \ldots, q_n\right]$, 加上坐標變換 $x^k=Q^T\left(w^k-w^{\star}\right)$, and $w^{\star}=A^{-1} b$

\[w^{k+1}=w^k-(A+\epsilon I)^{-1}\left(A w^k-b\right) \\ Q^T(w^{k+1} - w^*)= Q^T(w^k - w^*) - Q^T (A+\epsilon I)^{-1} \left(A w^k-b\right)\\ x^{k+1} = x^k - Q^T (QDQ^T+\epsilon Q Q^T)^{-1} Q D x^k \\ x^{k+1} = x^k - (D+\epsilon I)^{-1} D x^k\]

再來拆開每個坐標軸！ \(\begin{aligned} x_i^{k+1} & =x_i^k-\frac{\lambda_i}{\epsilon+\lambda_i} x_i^k \\ & =\left(1-\frac{\lambda_i}{\epsilon + \lambda_i}\right) x_i^k=\left(\frac{\epsilon}{\epsilon + \lambda_i}\right)^{k+1} x_i^0 \end{aligned}\)

其中 $x_i$ 對應 $q_i$ 坐標軸。

• 可以看到 $x^k$ 也會等比數列收斂到 0! 因爲 $\frac{\epsilon}{\epsilon + \lambda_i} < 1$. 但是和 GD 的方式不同 $(1-\alpha \lambda_i)<1$.

• 如果 $\epsilon \gg \lambda_i \to (1-\frac{\lambda_i}{\epsilon+\lambda_i}) \approx (1-\epsilon^{-1}\lambda_i) = (1-\alpha \lambda_i)$ 基本就是 gradient descent.

• PGD 的好處: 如果 $A$ 有 high condition number $\kappa \gg 1$, 也就是 ill-condition, 一般 GD 收斂非常慢或是計算 $A^{-1}$ 也不容易算精確。但是加上 $(A + \epsilon I)^{-1}$ 稱爲 regularized matrix 則沒有計算精確的問題 (always positive definite)!

Advanced Optimization with Adaptive Step (不僅僅用於二次式)

二次式是簡單的 case, 因為二次微分 (Hessian) 為定值。因此步長 $\alpha$ (以及 momentum when $\beta \approx 1$ ) 可以 (也只需要) 是定值。

對於一般複雜的非二次式，我們不知道二次微分導數 (Hessian)。通常二次導數也非定值，所以需要用 adaptive 方法估計步長 $\alpha$（and $\beta$？）才能快速收斂。

我們再看深度學習中更常用的加速算法。

我們先用直觀方法。SGD 基本類似 GD ($x_{k+1} = x_k - \alpha_k \nabla f(x_k)$ )。有兩個原則決定 $\alpha_k$

• $\alpha_k$ 應該開始比較大以加速收斂，隨著$k$ 越大會越小以得到好的準確度。
• $\alpha_k$ 應該和 $f(x_k)$ 的二次微分 (Hessian) 成反比。二次微分小，代表比較平直，$\alpha_k$ 可以比較大，反之則比較小。
• 利用二階牛頓法 ($x_{k+1} = x_k - H^{-1} \nabla f(x_k)$). 如何近似 $H(x_k)$? 利用 Fisher information: $H(x_k) \approx \nabla f(x_k)^2$
  • 要估計 2nd order 倒數有困難。可以利用 Fisher information!! 2nd order derivative ~ (-1) * (1st order derivative)^2

我們看 AdaGrad 就是 $v_t = \sum_{i=1}^t g_i^2$ and $x_{t+1} = x_t - \frac{\alpha_t}{ \sqrt{v_t}} g_t$

AdaGrad 有兩個缺點

• Learning rate 會不斷變小，因為 $g_i^2$ 會越來越小。這會造成學不到新的東西
• 沒有 momentum 加速！

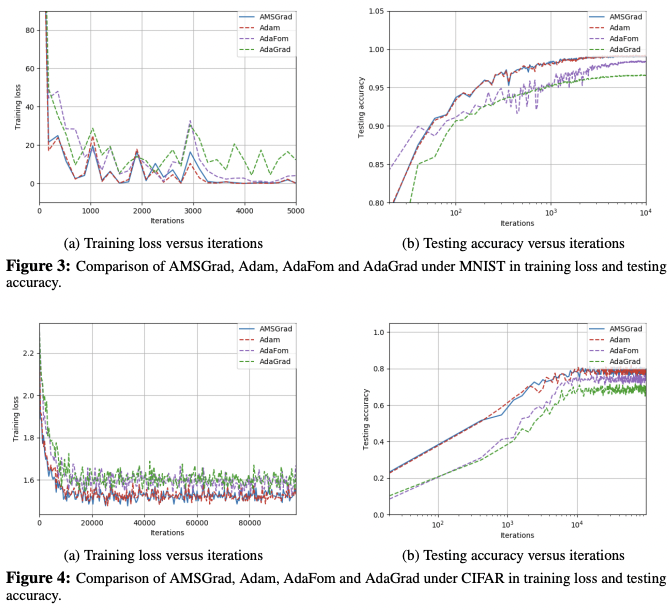
改善 1. 只要加入 momentum term 即可。AdaForm

改善 2. 利用 exponential weight of $g_t$, 讓新的 $g_t$ 佔的 weight 比較小。AMSGrad or RMSProp

同時改善 1 and 2. 就變成 Adam!

其中 $g_t$ 代表 gradient. $m_t$ 代表 exponentially weighted gradient estimate. 主要是多了一項 $(1-\beta)$ 讓 gradient 佔的比例變小。

另外多了一項 $v_t$, 可以視為 normalized $\alpha$? $\alpha_t/\sqrt{v_t}$ 稱為 effective stepsize.

Convex Function with L1 Regularization

因爲 L1 regularization 是非光滑函數。需要使用 Proximal algorithm.

如果使用 (sub)-gradient descent ,

Accelerated PGD

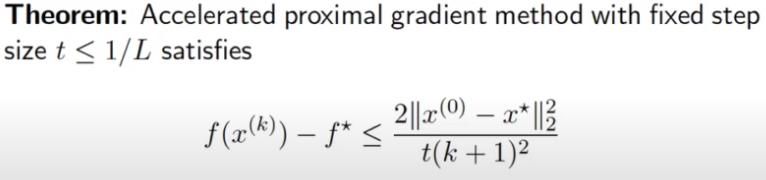
可以看到 L1 regularization 的 proximal gradient descent algorithm 稱爲 ISTA (Iterative Soft-Thresholding Algorithm) 和 gradient descent 主要的差異是多加了 soft-thresholding. 加上 soft-thresholding 的收斂速度和 GD 也就差不多。

顯然這不是最快收斂的算法，還可以再 accelerate! 就是 FISTA (Fast ISTA) for L1 regularization. FISTA 和 ISTA 的差異就是引入 momentum $v$. In general accelerated proximal gradient method 和 accelerated GD 主要的差異是多加 prox operator.

對於強凸函數 (e.g. quadratic function) with (非光滑) L1 regularization.

• (Sub)-gradient descent Error Converge Rate: $O(1/\epsilon^2)$

• Proximal gradient Error Converge Rate: $O(\log (\frac{1}{\epsilon})/\log(\frac{1}{\gamma_{GD}}))$

• Accelerated proximal gradient Error Converge Rate: $O(\log (\frac{1}{\epsilon})/\log(\frac{1}{\gamma_{AGD}}))$

對於一般光滑凸函數 + 非光滑 proximal friendly 函數。

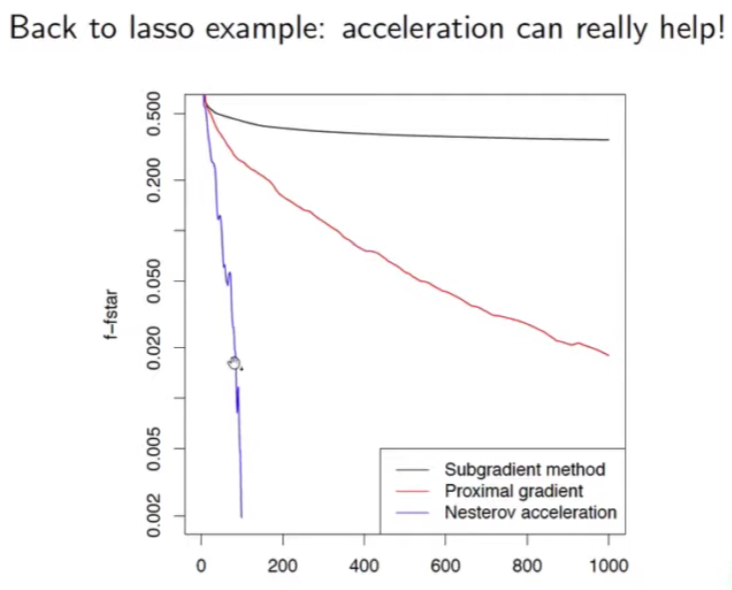
• (Sub)-gradient descent Error Converge Rate: $O(1/\epsilon^2)$，如下圖黑綫
• Proximal gradient Error Converge Rate: $O(1/{\epsilon})$ ，如下圖紅綫
• Accelerated proximal gradient Error Converge Rate: $O(1/{\sqrt{\epsilon}})$ ，如上面公式，如下圖紫綫 (?)