Optimization - Manifold Gradient Descent

Source

https://www.youtube.com/watch?v=lK62DwSIjXA&ab_channel=FMGDataDrivenControlSummerSchool

excellent tutorial on differential geometry and manifold optimization!!

https://openreview.net/pdf?id=H1GFS4SgUS

Introduction

爲什麽要做 manifold optimization.

已知的 manifold, 直接在 manifold 做 optimization. 而非 use it as a constraint. 如果是 well behaved manifold. Hopefully manifold optimization 可以更有 insight.
如果是未知的 manifold, 也許可以用 manifold learning 先學到的 manifold. 這個 manifold 可以用於之後的 inference.
很多 matrix 問題 (例如 recommendation system) 其實也可以視為 manifold 問題

拜 Einstein 之賜，force，就是 gradient 也可以視爲是 curved space! 所以似乎也可以把 manifold 整合在一些 optimizer 之中。例如 https://openreview.net/pdf?id=H1GFS4SgUS

The AGM method can be seen as the proximal point method applied in this curved space.

微分幾何 (Differential geometry) 是必備的知識。幾個 key concept。

問題描述

一般歐式幾何的 optimization 問題定義如下。$S \in \mathbf{R}^n$ 而且大多是 convex set.

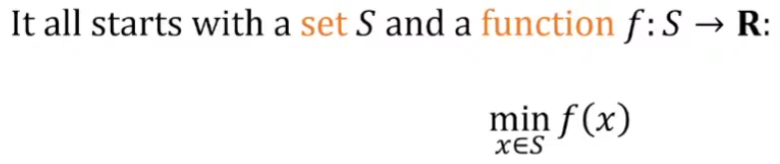
Unconstrained optimization: $S = \mathbf{R}^n$

Manifold optimization 的描述如下。基本和一般 optimization 一樣。只是加上 manifold constraint.

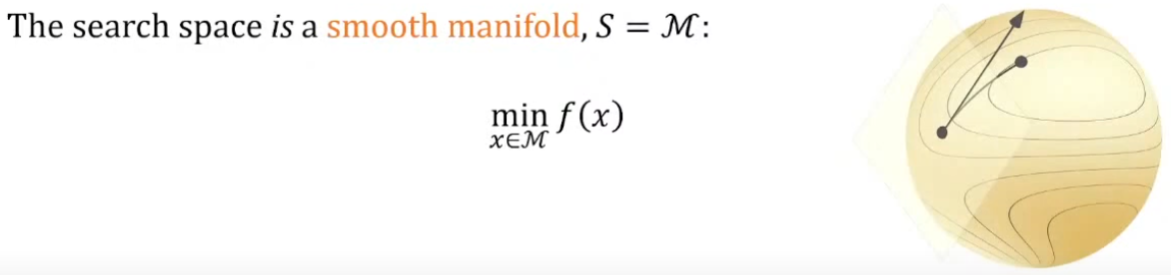
此處 $M$ 是 Riemannian manifold. 另外假設 $f$ 是 differentiable 存在 Riemannian gradient and Hessian.
更好的描述是 matrix！如下
- Rotation group 就是選擇的 operation. 很容易想像是 Remannian.
- Stiefel manifold 是 low rank 的 manifold, 常用於 recommendation system (?).

Manifold	Matrix Representations
Stiefel manifold	$\mathcal{M}={X \in \mathbf{R}^{n \times p}: X^{T} X=I_p }$
Rotation group	$\mathcal{M}={X \in \mathbf{R}^{3 \times 3} : X^{T} X=I_3 \text{ and }\operatorname{det}(X)=+1 }$
Grassman manifold	$\mathcal{M}=$ {subspaces of dimension $d$ in $\mathbf{R}^n$ }
Fixed-rank matrices	$\mathcal{M}={X \in \mathbf{R}^{m \times n}:\operatorname{rank}(X)=r}$
Positive definite matrices (convex)	$\mathcal{M}= {X \in \mathbf{R}^{n \times n}: X=X^{T} \text{ and } X \succ 0}$
Hyperbolic space	$\mathcal{M}={x \in \mathbf{R}^{n+1} :x_0^2=1+x_1^2+\cdots+x_n^2}$

Manifold Optimization

有兩種看法

假設我們有 global view (也就是 global coordinate) in 歐式空間。這就回到 $x \in S$. 這和 manifold optimization 其實沒有關係。optimization 基本兩個 steps
- (Linear) gradient descent 從 $x^{k+1} = x^{k} - \alpha \nabla f$.
- Reprojection $x^{k+1}$ 到 $M$
微分幾何並不假設有 global coordinate, 而是只有 local coordinate. 這就無法由
- (Linear) gradient descent 從 $x^{k+1} = x^{k} - \alpha \nabla f$.
- Retraction $x^{k+1}$ 到 $M$

微分幾何 Differential Geometry Key Concept

Smooth manifold

Matrix representation

Manifold	Matrix Representations
Stiefel manifold	$\mathcal{M}={X \in \mathbf{R}^{n \times p}: X^{T} X=I_p }$
Rotation group	$\mathcal{M}={X \in \mathbf{R}^{3 \times 3} : X^{T} X=I_3 \text{ and }\operatorname{det}(X)=+1 }$
Grassman manifold	$\mathcal{M}=$ {subspaces of dimension $d$ in $\mathbf{R}^n$ }
Fixed-rank matrices	$\mathcal{M}={X \in \mathbf{R}^{m \times n}:\operatorname{rank}(X)=r}$
Positive definite matrices (convex)	$\mathcal{M}= {X \in \mathbf{R}^{n \times n}: X=X^{T} \text{ and } X \succ 0}$
Hyperbolic space	$\mathcal{M}={x \in \mathbf{R}^{n+1} :x_0^2=1+x_1^2+\cdots+x_n^2}$

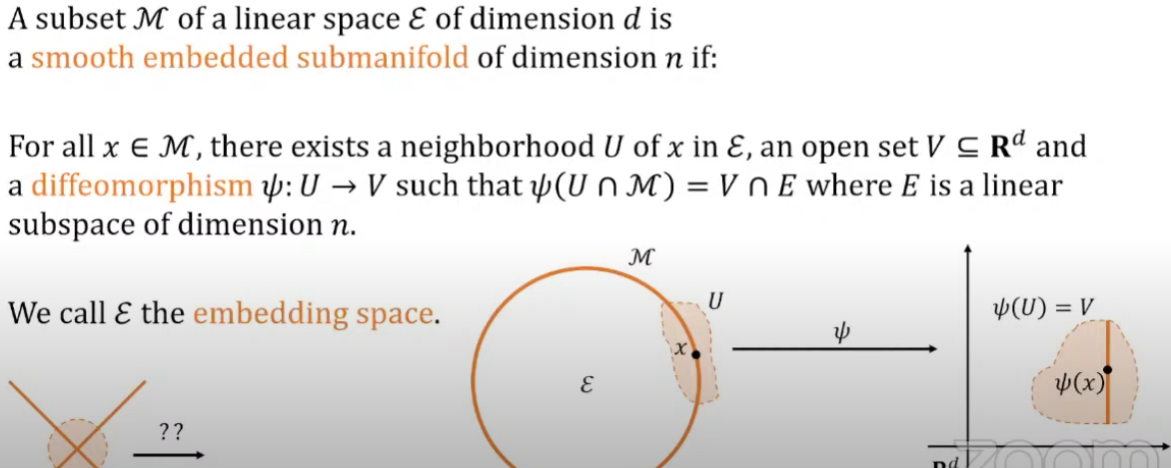
What is a manifold?

Smooth embedded sub-manifold of dimension $n$

Manifold 基本就是局部的 (平滑) 空間近似歐式 (平直) 空間。數學的定義：$U \in \mathcal{E}$ (2D in 下圖) 是包含 $x$ 的 open set，但大於 local $\mathcal{M}$ (1D in 下圖). 存在一個 function $\psi$ 可以 map $U$ and local $\mathcal{M}$ to a flat and linear space $V$包含 $\psi(x)$.

(Smooth manifold can be linear) Tangent Space $T_xM$

因為 manifold 是 smooth and flat! 所以可以定義 linear tangent space
Linear tangent space 的 dimension 和 manifold 的 dimension 相同！以下圖為例 manifold 2D; tangent pace is 2D.
如何找出 talent space 的 base? 利用 parameterized line! 可以找出所有 tangent vectors. $T_xM = ker Dh(x)$

Tangent Bundle $TM$

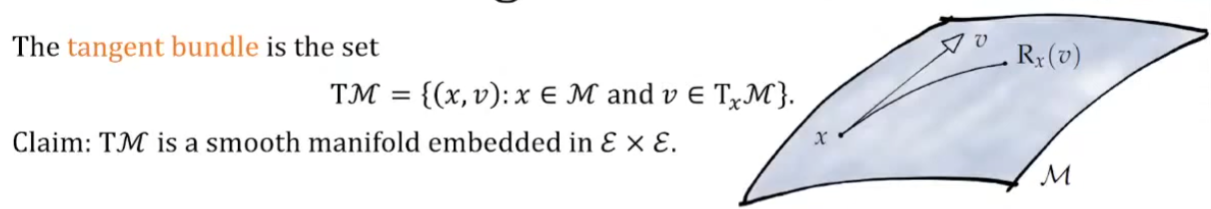
Manifold Differential

Riemannian Gradient

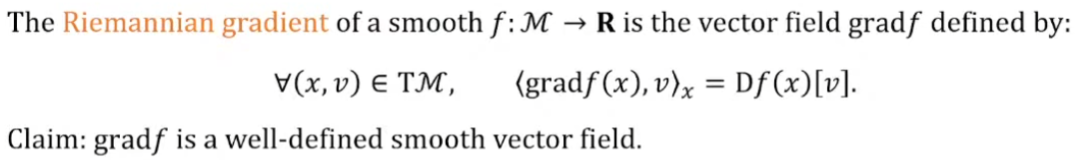
Directional derivative

Riemannian Hessian

Connection

首先在 manifold 可以定義 geodesics, 等價於歐式空間的”直線”。

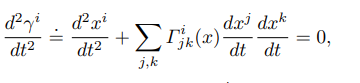
接下來可以定義 “geodesics convexity” 等價於歐式空間的 convexity.

Metric and Curvature

Manifold Optimization

基本有兩個 steps:

Tangent space $T_p M$ 先做 gradient descent. $s_k = x_k - \alpha <grad f(x)>)$?
Retraction

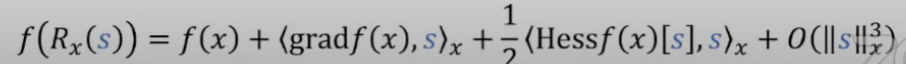
基本上 proximal gradient descent 可以視爲是 manifold gradient descent 的特例？（L2 norm regulation 可以視爲 manifold? or kernel?)

或僅是兩者的形式相同？

unconstraint convex function -> convex function + convex constraint -> convex function + manifold constrain (but not necessarily convex constraint!)

Example: Rayleigh quotient optimization

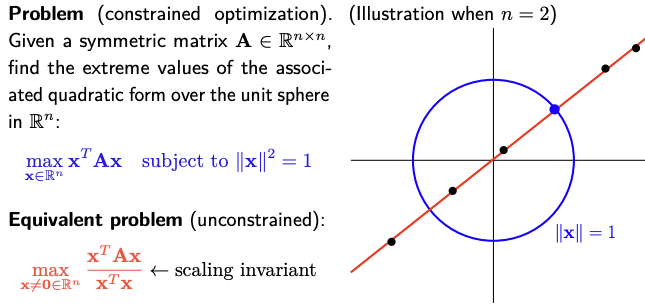
Compute the smallest (or largest) eigenvalue of a symmetric matrix $A \in \mathbf{R}^{n \times n}$ :

\[\min _{x \in \mathcal{M}} \frac{1}{2} x^{T} A x \quad \text { with } \mathcal{M}=\left\{x \in \mathbf{R}^n: x^{T} x=1\right\}\]

注意上述問題沒有要求 $A$ 是 positive semi-definite matrix；因為有 manifold 的限制，所以 max or min 都一定存在。
- 不過正統的 Rayleigh quotient 似乎是 max。稱為 quotient 是因為除以 norm!
- 先說結論：max or min 就是最大或最小的 eigenvalues (不考慮 1/2 factor)，這個結果似乎很直觀假設 $A = Q^T D Q$
- 當然對應的 $x$ 就是 Eigenvectors.
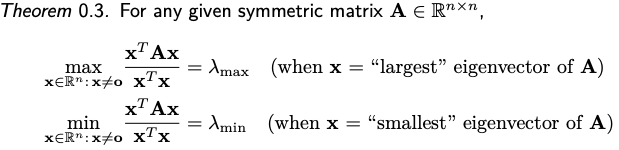
Rayleigh quotient 問題很自然可以轉換成 manifold optimization. 只要把球面 constraint 變成 manifold.
The cost function $f: \mathcal{M} \rightarrow \mathbf{R}$ is the restriction of the smooth function $\bar{f}(x)=\frac{1}{2} x^{T} A x$ from $\mathbf{R}^n$ to $\mathcal{M}$.
Tangent spaces $\quad T_x \mathcal{M}={v \in \mathbf{R}^n: x^{T} v=0 \text{ where } x^T x = 1}$.

Make $\mathcal{M}$ into a Riemannian submanifold of $\mathbf{R}^n$ with $\langle u, v\rangle=u^{T} v$.

Projection to $T_p M$ : $\quad \operatorname{Proj}_x(z)=z-\left(x^{T} z\right) x$.
Gradient of (包含 1/2 factor) $\bar{f}: \quad \nabla f(x)=A x$.
(Manifold) Gradient of $f$ : $\quad \operatorname{grad} f(x)=\operatorname{Proj}_x(\nabla \bar{f}(x))=A x-\left(x^{T} A x\right) x$.
Differential of gradf: $\operatorname{Dgrad} f(x)[v]=A v-\left(v^{T} A x+x^{T} A v\right) x-\left(x^{T} A x\right) v$.
Hessian of $f$ : $\operatorname{Hess} f(x)[v]=\operatorname{Proj}_x(\operatorname{Dgrad} f(x)[v])=\operatorname{Proj}_x(A v)-\left(x^{T} A x\right) v$.