Optimization - NN Optimization

Source

https://www.ruder.io/optimizing-gradient-descent/ [@ruderOverviewGradient2016]

Introduction

神經網絡是非凸函數，因此 optimization 理論上困難。不過我們一般還是利用凸函數優化的方法用於神經網絡。

Stochastic Method

我們把原來的問題重新 formulate to fit 常見的機器學習優化問題。

原始的問題: $\min_x L(x)$, $x \in \R^n$

在機器學習中，我們有 N 個 labeled data. Loss function 改成 $L(x) = \frac{1}{N}\Sigma_{i=1}^N f_i(x)$

$f_i(x)$ 可以是 regression loss function (L2 norm or logistic regression function), classification function (entropy function)。基本都是凸函數。

$\min_x L(x) = \min \frac{1}{N} \sum^N_{i=1} f_i(x) = \min_x \sum^N_{i=1} f_i(x)$, $x \in \R^n$

此處的 $N$ 是機器學習的 samples; $x$ 是 weights, $n$ 是 number of weight.

一般 N 非常大，可以是幾百萬。同時 $N \gg n$.

如果使用 GD, 每一次迭代，最低的代价也要算一次梯度。如果 N 很大的时候，算一次完整的函数梯度都费劲，这时候就可以考虑算部分函数梯度。如果這些 sample 都是 independent, 部分函數的梯度法也會收斂到完整函數的梯度法。

一階方法：Stochastic Gradient Descent (SGD)

\[\begin{aligned}x^{k+1} & =\arg \min \left\{f_{i_k}\left(x^k\right)+<\nabla f_{i_k}\left(x^k\right), x-x^k>+\frac{1}{2\alpha^k} \|x-x^k\|^2\right\} \\& =x^k-\alpha^k \nabla f_{i_k}\left(x^k\right)\end{aligned}\]

此處 $i_k \in 1, \cdots， N$

Mini-batch

\[\begin{aligned}x^{k+1} & =x^k-\alpha^k \nabla f\left(x^k; x^{(i:i+n-1)}, y^{(i:i+n-1)}\right)\end{aligned}\]

一個更常用的變形是 mini-batch, 也就是用多個 samples, 通常是 16/32/…/256, 計算 gradient.

Optimization - NN Optimization

Source

Introduction

Stochastic Method

一階方法：Stochastic Gradient Descent (SGD)

Mini-batch

SGD Variation

Momentum method

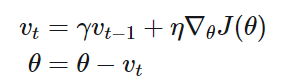
Nesterov Accelerated Gradient

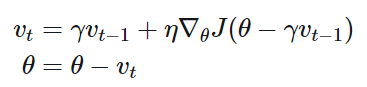
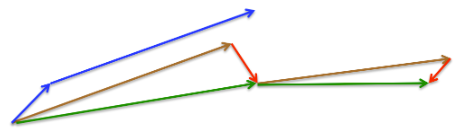
Adam

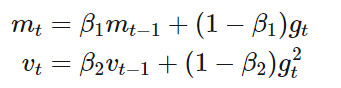
其他一系列的 stochastic GD 變形