作為電機專業戶,最熟悉的就是大名鼎鼎的馬克士威電磁方程 (Maxwell equations) 和向量微積分、波動方程、等一系列相關公式。我們也常常聽到馬克士威電磁方程和狹義相對論相容,像是兩者都符合 Lorentz transform。甚至愛因斯坦也是從馬克士威電磁方程得到靈感開創狹義相對論。
像是牛頓運動定律符合 Galileo transform 但不符合 Lorentz transform, 因此牛頓力學需被狹義相對論修正。
馬克士威電磁方程則是天生符合 Lorentz transform 而相容於狹義相對論。
除了 Lorentz transform 是否有更接地氣的說明兩者的相容性?
我們先看
狹義相對論的兩大支柱
- 光速 $c$ 在任何 (慣性或非慣性) 座標系不變,例如觀察者(座標系)的運動速度為 $v$, 看到的光速也是 $c$, 不是 $c\pm v$.
- 物理定律在任何慣性座標系都是等價,沒有“黃金座標系”。
我們就從這兩個角度檢驗馬克士威電磁方程。
- 狹義相對論兩個最重要的結論就是:(1) 尺縮和時膨; (2) 質能互換 $E=MC^2$.
光速 $c$ 在任何 (慣性或非慣性) 座標系不變
Maxwell equation 最重要的推論就是在真空中光速 = $ \frac{1}{\sqrt{\mu_o \epsilon_o}} = c $. 非常關鍵就是 $\mu_o$ and $\epsilon_o$ 分別是真空的介電常數 (vacuum permittivity) 和磁導率 (vacuum permeability),這兩個數字都和觀察者 (座標系) 運動速度無關!因此 (真空) 光速在任何座標系都是一個定值。這似乎直接證實狹義相對論的一個支柱。
問題是如果這麼簡單,為什麼其他物理學家沒有發現光速是和座標系這麼重要的事?
另外其他的波動,例如聲波或水波,的波速公式難道和慣性座標系的運動速度有關?
聲波、介質、以太
我們先看聲波,wiki https://en.wikipedia.org/wiki/Acoustic_wave#Acoustic_wave_equation
acoustic velocity $c_s$ (sound speed) is given by the Newton-Laplace equation: \(c_{s}={\sqrt {\frac {C}{\rho }}}\)
where
- C is a coefficient of stiffness, the bulk modulus (or the modulus of bulk elasticity for gas mediums),
- $\rho$ is the density in $kg/m^3$
$C$ 和 $\rho$ 顯然和觀察者座標系無關,難道我們也可以推論聲速 $c_{s}$ 也和觀察者運動速度無關 ?!
重點是這些波動都有介質,例如空氣,水。因此所謂波速都是相對介質靜止而言。
所以對於有介質的波動,可以先有一個黃金座標系:就是觀察者運動速度相對介質為 0 的座標系,得出波速的公式 (如上式)。顯然這個公式不會包含座標系運動速度 (因為運動速度是 0)。對於其他的觀察者慣性座標系速度 $v\ne 0$ , 只要後處理再加上相對速度即可 : 例如 Galileo 相對性,聲速1就是 $c_s \pm v$.
如果相對介質有運動,就需要修正,如果是和波動反向,看到的波速增加,因此頻率增加 (波長不變)。如果同向,則波速變慢,因此頻率降低。這是著名的 Doppler 效應 (formula TBD).
但如果光是在“真空”沒有任何介質,顯然無法定義所謂“黃金座標系”,所有慣性座標系看到的光波就變成都是 $c$. 這個結論對當時的物理學家太奇怪,因此提出了“以太假說”。就是沒有所謂真空,光波不是在真空中傳播,而是在以太中傳播2。就如同聲波在空氣中傳播。回歸到光速 $c$ 只是對於觀察站運動速度相對於以太為 0 看到的波速。
接下來就是一連串以太實驗,卻反而證明以太不存在。以及愛因斯坦橫空出世,提出狹義相對論的兩個支柱,包含光速在所有座標系都是 $c $ 的前提。
物理定律在任何慣性座標系都是等價,沒有“黃金座標系”
因為任何慣性座標系代表不同的相對速度,所以任何物理定律包含速度 ($v$) 項都需要被仔細檢驗。不然不同慣性座標系觀察者的速度不同就會看到不同的物理定律。
馬克士威電磁方程本身只包含電場和磁場。也沒有速度相關的 term, 因此初步 OK. 但有一個 well-known Lorentz force 公式,其中磁力部分就和速度成正比。
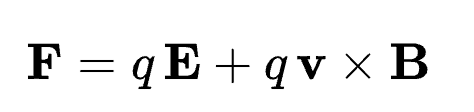
也就是不同慣性座標系的觀察者會看到不同的 Lorentz force? 這合理嗎?
以下圖為例:一個電子 -q 由左往右移動 with velocity $v$. 沒有電場 E, 但有一個定磁場 B 破出紙面。[@wanxiangMagneticForce2022]
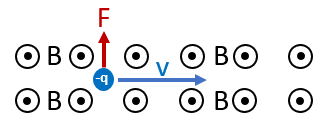
對於靜止的觀察者 Alice 看到的 Lorentz force 是 $q \mathbf{v} \times \mathbf{B}$,利用左手定則得出向上的力 F 會將電子往上偏。
但對於運動速度 $v$ 的慣性座標系觀察者 Bob 而言,他看到是一個靜止沒有運動的電子,所以 Lorentz force 中的磁力為 0. 因此電子不會往上偏。
到底電子是否會往上偏?如果往上偏,這是否違反物理定律在任何慣性座標系等價?
磁力或是磁場相容於慣性座標系嗎?
這個問題之前困擾我,但我是不求甚解。基本上我相信電子會往上偏,就像所有的教科書都會告訴你如此。但如何解釋 Bob 這個慣性座標系看到的奇怪現象:一個 (相對於 Bob 的慣性座標系) 靜止的電子莫名其妙的往上偏?
這個問題的 catch 在於定磁場 B 不能假設是和慣性座標系觀察者無關!或者說不同的慣性座標系 Alice 和 Bob 會看到不同的電場和磁場。要瞭解爲什麽,必須要把磁場的來源考慮進來。
我們看具體的例子:磁場 B 可以由電流 I 產生。我們假設一根導線在電子的下方 with current I 向右方. 根據安培右手定則在運動電子的位置會有磁場突出紙面,符合上述的實驗。
為了解釋方便,我們假設電流是由向左移動的電子 (-q) 和向右移動的正電子3 (+q) 所構成,兩者的速度為 $\pm u$. To make the experiment complete, 我們可以假設這個導線非常非常長,且在很遠的地方連上電池成為迴路。整個實驗是一個封閉的系統。
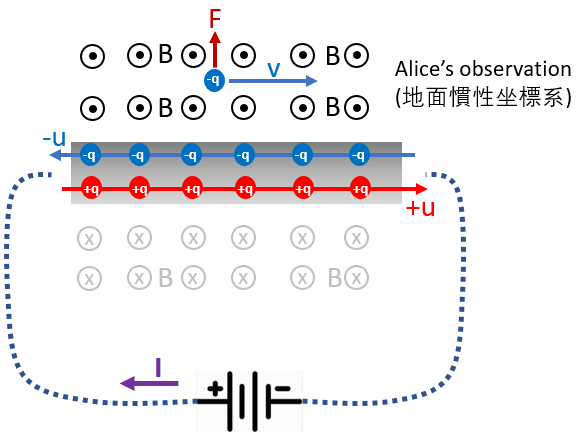
對於 Alice (靜止或地面慣性座標系) :
(Trivial) Case 1, I = 0: 導綫内的正負電荷的速度 $u=0$。正負電荷密度都是 $\lambda_o$, 相互抵消净電場為 0。因此不會對外界運動電子產生電力。同時因爲 I = 0, 也沒有磁場 B = 0, 因此也沒有磁力。運動電子維持等速直綫運動。
Case 2, I > 0: 導綫内的正電荷以速度 $u$ 向右移動,負電荷以速度 $u$ 向左移動。雖然這個模型有點不實際,但計算很好用。從地面觀察者 Alice 來看,由於狹義相對論的尺縮效應,電荷之間的距離會縮小,因此綫密度會變大。但由於正電荷和負電荷速度大小一樣,因此它們的綫密度都為 λ,淨電荷密度為零,净電場為 0,不會對外界帶電粒子產生電力。
\[\lambda=\frac{\lambda_0}{\sqrt{1-\frac{u^2}{c^2}}} \quad and \quad I=2 \lambda u\]對於 Bob (和導綫外電子綁定的慣性座標系,相對地面運動速度 v) :
現在, 我們把參考系和導線外的帶電粒子綁定在一起,如下圖:
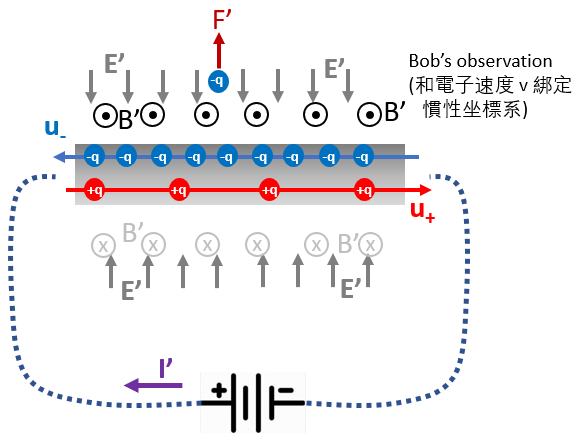
在這個參考系下的 Bob 會看到一個靜止的導綫外電子。但在導綫内的正電荷的移動速度大小 $\mathrm{u}{+}$ 與負電荷的移動速度大小 $\mathrm{u}{-}$ 不同。因此兩個正電荷之間的距離與兩個負電荷之間的距離不同, 導致正電荷的綫密度 $\lambda_{+}$ 就與負電荷的綫 密度 $\lambda_{-}$ 不同。所以, 導線的橫截面就會有淨電荷產生,會產生一個向内的净電場。同時對導線外的電子產生向上的靜電力! \(\begin{gathered} u_{+}=\frac{u-v}{1-v u / c^2} \quad \text { and } \quad u_{+}=\frac{u+v}{1+v u / c^2} \\ \lambda_{+}=\frac{\lambda_0}{\sqrt{1-u_{+}^2 / c^2}} \text { and } \quad \lambda_{-}=\frac{\lambda_0}{\sqrt{1-u_{-}^2 / c^2}} \end{gathered}\) 把以上的等式結合起來, 我們能得到淨電荷密度 $\lambda_{t}$ 的公式 : \(\lambda_t=\lambda_{+}-\lambda_{-}=-\frac{2 \lambda u v}{c^2 \sqrt{1-v^2 / c^2}} \neq 0\)
由上式我們可以看出,確實電荷密度不為零,所以會產生電場,帶電粒子就會受到靜電力。閉合曲面內的電荷分佈與產生的電場之間的關係可以由高斯定理算得。因此,我們沿著導線做一個半徑為r的圓柱面,根據高斯定理,可以得到帶電粒子處的場強,然後就可以得到粒子所受的靜電力:
\[\begin{aligned} &E^{\prime}=\frac{\lambda_t}{2 \pi \epsilon_0 x}=-\frac{\lambda u v}{\pi \epsilon_0 x c^2 \sqrt{1-v^2 / c^2}}\\ &F^{\prime}=E^{\prime} q=-\frac{\lambda u v q}{\pi \epsilon_0 x c^2 \sqrt{1-v^2 / c^2}} \end{aligned}\]接下來我們要用到麥克斯韋方程組推導出來的光速公式 $c^2= 1/{\epsilon_{0} \mu_{0}}$ 和上述提到的電流公式 $I=2 \lambda u$ 對受力公式進行替換 , 可以得到 :
\[F^{\prime}=-\frac{\mu_0 Ivq}{2 \pi x \sqrt{1-v^2 / c^2}}\]請注意,這裏的 F’ 是在和帶電粒子綁定的坐標系,也就是 Bob 坐標系。我們需要把它轉換到地面觀察者 Alice 的坐標系:
\[F=F^{\prime} \sqrt{1-v^2 / c^2}=-\frac{\mu_0 I v q}{2 \pi x}\]這就是與洛倫茲力相同的靜電力, 只不過在地面觀察者看來, 這像是導線電流產生的硑場而導致的力。我們還可以讓它和洛倫茲力的公式相等, 就能得到導線產生的磁場強度
\[\begin{aligned} &F=-\frac{\mu_0 I v q}{2 \pi x}=-B v q\\ &B=\frac{\mu_0 I}{2 \pi x}\\ \end{aligned}\]這看起來是不是很熟悉,就是我們高中學過的畢歐一薩伐定律
Q: I, B, $\lambda$是否也改變? Check it.
結論
-
磁力(不是磁場)可以從狹義相對論在不同慣性坐標系產生。
-
Lorentz force (包含電力和磁力) 在不同慣性坐標系都是不變。但是磁力可能轉爲電力!
Question: 所以可以説磁力遠弱與電力是因爲由相對性產 生嗎? (v/c) factor?
那如何解釋磁性物質,Hall effect or anti-Hall effect material?
Futher Study
以上是 (quasi-) stationary 的情況,從 Maxwell equation 就是靜電和靜磁場。狹義相對論的“尺縮”效應就可以解釋。
比較進階:把上述的連續電流改成 1 個電子的流動,請問如何解釋電磁力 observed by Alice and Bob? 此時不是 quasai-stationary 而是 time varying 運動,需要考慮尺縮和時膨效應。可以參考:
磁真的存在吗?为什么磁力是幻觉? https://youtu.be/q-1U5ORaIA8
Reference
萬象經驗 2022. “磁性是怎么从狭义相对论中产生的.” October 9, 2022.