Geometric Deep Learning

Posted on | In

Introduction

2016年，牛津大學教授、Twitter的圖機器學習研究負責人Michael Bronstein發佈了一篇論文，首次引入幾何深度學習（Geometric Deep Learning, GDL）一詞，試圖從對稱性和不變性的視角出發，從幾何上統一CNNs、GNNs、LSTMs、Transformers等典型架構的方法。

這應該是物理學家和數學家的夢想。就像對稱性成為現代物理學的基石。至少對我非常有吸引力。

CNN -> translation equivariance (or invariance)

GNN -> graph ?

LSTM -> time equivariance (or invariance)?

Transformer -> position invariance -> need positional encoding

Bronstein 之後吸引一批數學物理學家如 Max Welling 找到 AI 切入點。

最好能把上述的統一理論再比較腦神經科學。

最近 Bronstein 在 Medium 發表四篇專欄文章。從古希臘幾何到物理、化學，再到現代圖神經網絡，詳細介紹了幾何深度學習（GDL）背後的思想是如何出現的。

第一篇 On the Shoulders of Giants, 主要討論對稱性的概念如何促進理論物理學的發展，第二篇 The Perceptron Affair, 為神經網絡的早期歷史和第一個「AI寒冬」，第三篇主要研究第一個「幾何」架構，第四篇討論了1960年代化學領域中GNN的早期原型。

image-20220820174855393

我們摘錄這四篇專欄的重要内容。

I. On the Shoulders of Giants

兩個重點：

(1) Felix Klein’s Erlangen Program 利用研究不變性定義並統合幾何學

  • 克萊因 (Klein) 的突破性見解是將幾何學的定義作為不變性的研究，或者換句話說，是在某種類型的轉換 (對稱性) 下保留的結構。

  • 克萊因 (Klein) 使用群論定義此類轉換，並使用群及其子群的層次結構來分類由此產生的不同幾何形狀。如下圖：Euclidean geometry invariant group 是 Affine geometry 的 subgroup, 依次是 Projective geometry 的 subgroup. 這有一點像現代代數的 field, ring, group 的關係。或是 Galois field 的 extended field 對應的 solvable group 之間的關係。

image-20220821113331220

  • 因此，一組剛性運動變換 (Iso-transformation) 導致傳統的歐幾里得幾何，而仿射 (Affine) 或投影 (Projective) 變換分別產生仿射和投影幾何。 Erlangen程序僅限於齊次空間，並最初排除了黎曼幾何。
  • Erlangen Program 將幾何學作為研究在某些類型的變換下保持不變的屬性的方法。 二維歐幾里得幾何形狀由保留區域，距離和角度以及平行度的剛性變換定義。 仿射變換保留平行性，但距離和面積均不保留。 最後，射影變換具有最弱的不變性，僅保留了相交和交叉比率，因此，克萊因認為射影幾何是最通用的一種。

image-20220821120925425

(2) 對稱性可以推導守恆律，這是一個令人驚訝的結果，被稱為 Noether 定理

  • Noether 證明了這一基本原理。通過規範不變性的概念（由Yang 和 Mills在1954年提出的廣義形式）成功地統一了除重力以外的所有自然基本力。 這就是所謂的標準模型，它描述了我們目前所知道的所有物理學。

  • What does it mean? 就是歐幾里得幾何公理以及所得出任何定理經過剛性轉換 (平移+旋轉) 都不變 (invariant == symmetry –> 有守恆量嗎?) . 仿射幾何的任何定理經過仿射變換也都不變，依次類推。就如同物理定律經過平移轉換或旋轉轉換都不變 (invariant == symmetry –> 動量守恆和角動量守恆)

幾何學分類及其對稱性和不變性總結表

幾何類型 對稱性 不變性
歐幾里得幾何 平移對稱、旋轉對稱、反射對稱 距離、角度、平行性、垂直性
仿射幾何 仿射變換（包括平移、縮放、旋轉、剪切） 平行線的長度比（仿射比）、共線性、平行性
射影幾何 射影變換（包括透視變換和homography） 共線性、四個共線點的交比
雙曲幾何 雙曲等距變換（雙曲旋轉、平移、反射） 雙曲距離、角度、無限多條不相交於給定直線的平行線
橢圓幾何 橢圓等距變換（球面旋轉、反射） 橢圓距離、角度、所有直線最終相交
黎曼幾何 等距變換（根據特定流形不同，如球對稱性） 黎曼度量、曲率
拓撲學 同胚變換（保持空間結構的連續變形，如拉伸、彎曲） 連通性、緊緻性、連續性、拓撲不變量（如層數）
分形幾何 自相似性（形狀在每個尺度上都呈現相似模式）、尺度不變性、遞歸對稱性 分形維度、統計自相似性、縮放律
複幾何 雙曲旋轉、縮放、反射 複數空間中的距離、角度、複變函數理論的各種不變量

這張表格總結了不同幾何類型的對稱性和不變性，幫助更清晰地理解每種幾何的特性。

幾何深度學習

深度學習領域的現狀讓我們想起了19世紀的幾何情況：一方面，在過去的十年中，深度學習在數據科學領域帶來了一場革命， 以前認為可能無法完成的許多任務 - 無論是計算機視覺，語音識別，自然語言翻譯還是 Alpha Go, 都能夠應用深度學習解決。另一方面，我們現在擁有一個針對不同類型數據的不同神經網絡體系結構的 model zoo，但統一原理很少。 很難理解不同方法之間的關係，這不可避免地導致相同概念的重新發明。

幾何深度學習指的是最近提出的 ML 幾何統一的嘗試，類似於 Klein 的 Erlangen program.

它有兩個目的：首先，提供一個通用的數學框架以推導最成功的神經網絡體系結構；其次，給出一個建設性的程序，以有原則的方式構建未來的體系結構。

在最簡單的情況下，監督機器學習 (supervised ML) 本質上是一個函數估計問題：給定訓練集上某些未知函數的輸出 (例如標記的狗和貓圖象)，人們試圖從某個假設類中找到一個適合訓練的函數 f，並可以預測以前看不見的輸入的輸出。 在過去的十年中，大型，高質量的數據集 (如ImageNet) 的可用性與不斷增長的計算資源 (GPU) 吻合，從而允許設計功能豐富的類，這些類可以內插此類大型數據集。

image-20220821215956215

II. The Perceptron Affair

神經網絡似乎是合適的選擇: 1958 Rosenblatt 提出一種 neural network 稱爲 perceptron 用於分類幾何形狀。Perceptron 非常簡單如下。但被誇大 perceptron 可以用於 walk, talk, see, write, reproduce 等問題。 \(f(\mathbf{x})= \begin{cases}1 & \text { if } \mathbf{w} \cdot \mathbf{x}+b>0 \\ 0 & \text { otherwise }\end{cases}\) 不過在 1969 Minsky and Papert 所寫的書 “Perceptrons” 證明 (1-layer) perceptron 可以用於分類 linear separable 問題，但無法分類非 linear separable 的問題，最簡單的例子就是 XOR, 稱爲 Perceptron affair. 當時這件事打臉很大，變成所謂的第一次 AI hype.

解決 linear separable 問題很簡單，就是用兩層或多層的 perception. Cybenko (1989) 和 Hornik (1991) 證明使用兩層或多層 neural network 也可以生成密集類的功能，從而可以將任何連續函數近似為任何所需的精度-這種特性被稱為通用近似 (Universal Approximation)。但他們只給出存在性的證明，並沒有告訴如何找出這個 neural network nodes and weights. 也就是在早期 neural network 研究 learning algorithm 是一個 big challenge. 、

Rosenblatt 提出一個 learning algorithm 針對 1-layer perceptron. 另外 researchers 也有一些針對特定網絡的 learning algorithm.

Multi-layer Perceptron Learning - Back-propagation

再來就是 learning algorithm 的突破，backpropagation, 就是利用 loss function 計算 gradient of weights 並用 gradient descent-based optimzation technique to train neural network. 這也是 Hinton 的主要貢獻之一。

Curse of Dimensionality

Multi-layer neural network 雖然可以達成 universal approximation, 但沒有告訴我們要多大的網絡。一個質樸的想法就是用一個很大很深的神經網絡來近似任何函數。這會遇到另一個問題：curse of dimensionality, 或稱爲組合爆炸。注意 curve of dimensionality 和 overfitting 是完全不同的概念。

我們用幾個例子説明

  1. Classifier (分類器)

對於習慣 3 維空間的我們，可能有一點難想象 curse of dimensionality. 我們用一些分類器例子説明。

什麽是一個有效的分類器?

  • 下圖是一個直覺的例子。就是同一類 data of the same feature 聚集在一起，但不同類 data (with different features) 有一定的距離。這裏我們假設有顔色作爲分別。但 in general 必須考慮 unsupervised learning, 也就是 data 沒有顔色，完全靠 clustering 來分類。因此 data 的數量要足夠才能像 cluster.

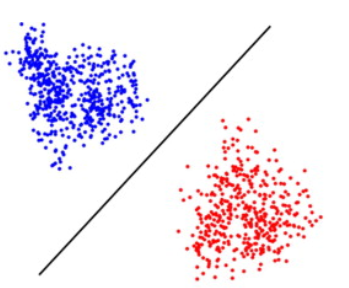
    image-20220822212425129

  • 什麼是 data of the same feature? 我們可以用單位圓 (unit sphere) 代表 feature space

    • For 2D (d=2), $\pi R^2$;
    • For 3D (d = 3), $\frac{4}{3} \pi R^3$​;
    • (Wrong!) 當 d 越來越大如下圖。先變大再變小。
  • 下一個問題是 space between two clusters, 用正立方體代表：

    • d=2, $R^2$;

    • d=3. $R^3$;

    • $R^d$ for d dimension.

  • 此時 data 的聚集度或是特徵 d(k) 遠大於 data 的 dimension N=2, d(k) » 2. 我們可以用 2D 的單位園 (unit sphere) 近似 d(k) ~ $\pi r^2 = \pi d^2$。另外可以用 d(N) ~ $(1^2 + 1^2) = 2$ 近似不同 group 的距離。

  • 3D 空間的 3 group:

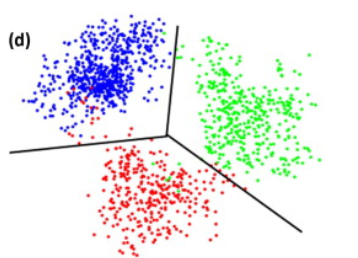
image-20220822213605205

image-20220822215152310

沒有回答

不過最後會要求 data 數量 » data 的 intrinsic dimensionality to make a meaningful classifer.

(Random) Sampling

作者：文兄 链接：https://www.zhihu.com/question/27836140/answer/141096216 来源：知乎 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

维数增多主要会带来的高维空间数据稀疏化问题。简单地说：

  • p=1，则单位球(简化为正值的情况）变为一条[0,1]之间的直线。如果我们有N个点，则在均匀分布的情况下，两点之间的距离为1/N。其实平均分布和完全随机分布的两两点之间平均距离这个概念大致是等价的，大家可稍微想象一下这个过程。
  • p=2，单位球则是边长为1的正方形，如果还是只有N个点 ，则两点之间的平均距离为$1n\sqrt{\frac{1}{n}}\sqrt{\frac{1}{n}}$。换言之，如果我们还想维持两点之间平均距离为1/N，那么则需N2N^2N^2个点。重點是可以把這個問題轉換成 2 維球體佔正方形的問題。
  • 以此类题，在p维空间，N个点两两之间的平均距离为$N−1pN^{-\frac{1}{p}}N^{-\frac{1}{p}}$，或者需要NpN^pN^p个点来维持1/N的平均距离。

由此可见，高维空间使得数据变得更加稀疏。这里有一个重要的定理：N个点在p维单位球内随机分布，则随着p的增大，这些点会越来越远离单位球的中心，转而往外缘分散。这个定理源于各点距单位球中心距离的中间值计算公式：

\[d(p,N)=(1−121N)1pd(p,N)=(1-\frac{1}{2}^{\frac{1}{N}})^\frac{1}{p}d(p,N)=(1-\frac{1}{2}^{\frac{1}{N}})^\frac{1}{p}\]

当p→∞时，d(p,N)→1。

很显然，当N变大时，这个距离趋近于0。直观的理解就是，想象我们有一堆气体分子，p变大使得空间变大，所以这些分子开始远离彼此；而N变大意味着有更多气体分子进来，所以两两之间难免更挤一些。

总之，当维数增大时，空间数据会变得更稀疏，这将导致bias和variance的增加，最后影响模型的预测效果。下图以KNN算法为例：

A good article:

https://www.visiondummy.com/2014/04/curse-dimensionality-affect-classification/

Two important points of DL

  1. Feature learning
  2. Back prop.

Curve of dimensionality 造成的後果

  • 神經網路不是越大越好，因為 dimensionality 是 n1 x n2 x n3 …基本變成 diaster 除非
    • 更多的 data : cost
    • regularization
    • 對稱性? CNN translation invariance/equivariance and share weights, not use Fully connected layer
    • Otherwise overfitting

下面是對第三、四篇的專欄文章翻譯。

傳統算法和深度學習算法的差異 - 不變性

我們都知道

我們澄清這裏的算法是 feature extraction (or feature learning for deep learning), 這是所有計算機視覺 (computer vision) 算法的基礎。Feature extraction 之後才能做, 物體偵測 (object localization and detection, position equivariant) 和分類 (classification, position invariant).

傳統算法的 feature extraction 例如 SIFT, ORB, HIST, …, 目前在 SLAM 算法還在應用。

Conventional algorithm flow:

Feature detection: corner/edge, lots of high frequency points.

Feature description: Add symmetric

Feature aggregation:

Classification:

image-20220820135206669

Con: take engineer to define/find; no invariance, need artificial defining invariant (angle, translation?)

Pro: Fast to compute, easy to debug?

Feature extraction FAST, ORB

Deep learning 算法

Pro: No engineer effort to define. translation equivariance is in CNN, but use data augmentation to train automatically.

Con: Need lots of data and computation to train. No intuition of black box behavior!

image-20220820135512961

and object detection

在計算機視覺問題（例如圖象分類）中可能最好地看到了這一點。即使是很小的圖象也往往具有很高的維度 (curse of dimensionality)，但是從直觀上講，當人們將圖象解析為向量以將其饋送到感知器時，它們會被破壞並丟棄很多結構。如果現在僅將圖象移位一個像素，則矢量化的輸入將有很大的不同，並且神經網絡將需要顯示很多示例，以瞭解必須以相同的方式對移位的輸入進行分類。

幸運的是，在許多高維ML問題的情況下，我們還有一個附加結構，它來自輸入信號的幾何形狀。我們稱這種結構為“先驗對稱性” (translation equivariant?)，它是一種普遍有效的原理，它使我們對因維數引起的問題感到樂觀。在我們的圖象分類示例中，輸入圖象x不僅是d維矢量，而且是在某個域Ω上定義的信號，在此情況下為二維網格。域的結構由對稱組 （在我們的示例中為2D平移組）捕獲，該組作用於域上的點。在信號 $\chi(\Omega)$ 的空間中，基礎域上的組動作（組元素， ∈ ）通過所謂的組表示ρ（ ）來表示，在我們的例子中，這只是移位運算符，作用於d維矢量的ad×d矩陣。

image-20220824215812014

幾何先驗的圖示：輸入信號（圖象x∈ （Ω））定義在域（網格Ω）上，其對稱性（平移組 ）通過組表示ρ（ ）在信號空間中起作用（移位算子 ）。 假設函數f（例如圖象分類器）如何與該組交互將限制假設類別。

輸入信號下面的域的幾何結構將結構強加給我們試圖學習的函數f。一個不變函數可以不受組的作用的影響，即對於任何 ∈ 和x，f（ρ（ ）x）= f（x）。另一方面，函數可能具有相同的輸入和輸出結構，並且以與輸入相同的方式進行轉換，這種情況稱為等變且滿足f（ρ（ ）x）=ρ（ ）f（x）[9]。在計算機視覺領域，圖象分類很好地說明了人們希望擁有不變函數的情況（例如，無論貓在圖象中的位置如何，我們仍然希望將其分類為貓），而圖象分割，其中輸出是逐個像素的標籤遮罩，是等變函數的一個示例（分割遮罩應遵循輸入圖象的變換）。

另一個強大的幾何先驗是“尺度分離” Scale invariant?。在某些情況下，我們可以通過“同化”附近的點並生成與粗粒度算子P相關的信號空間的層次結構，來構建域的多尺度層次結構（下圖中的Ω和Ω’）。尺度，我們可以應用粗尺度函數。我們說，如果函數f可以近似為粗粒度算子P和粗尺度函數f≈f′∘P的組成，則它是局部穩定的。儘管f可能依賴於遠程依賴關係，但如果它是局部穩定的，則可以將它們分為局部交互作用，然後向粗尺度傳播[10]。

image-20220824215743489

標度分離的示意圖，其中我們可以將細級函數f近似為粗級函數f’和粗粒度運算符P的組成f≈f′∘P。

General Geometric Architecture

這兩個原則為我們提供了一個非常通用的幾何深度學習藍圖，可以在大多數用於表示學習的流行深度神經體系結構中得到認可：典型設計由一系列等變層（例如，CNN中的卷積層）組成，可能遵循 通過不變的全局池層將所有內容彙總到一個輸出中。 在某些情況下，也可以通過採用本地池形式的粗化過程來創建域的層次結構。

image-20220821143003300

這是一種非常通用的設計，可以應用於不同類型的幾何結構，例如網格 (grid)，具有全局變換組的齊次空間，圖形（以及特定情況下的集合）和流形，其中我們具有全局等距不變性和局部性 規範的對稱性。 這些原則的實現導致了深度學習中當今存在的一些最受歡迎的體系結構：從平移對稱出現的卷積網絡 (CNN: translation equivariant - local pooling - translation equivariant - invariant global pooling)，圖神經網絡 (GNN: permutation equivariant - local pooling - permutation equivariant - invariant global pooling)，DeepSets [11]和Transformers [12]，實現了置換不變性， 時間扭曲不變的門控RNN（例如LSTM網絡）[13]，計算機圖形和視覺中使用的內在網格CNN [14]，它們可以從量規對稱性 (Gauge symmetry) 派生。

image-20220826222359199

如果說對稱性的歷史與物理學緊密地交織在一起，那麼圖形神經網絡的歷史，即幾何深度學習的典型應用代表則植根於自然科學的另一個分支：化學。

自19世紀中期以來，化學家們已經建立了一種能夠普遍被接收的理解方式，通過結構式來指代化合物，表明化合物的原子、它們之間的鍵，甚至它們的三維幾何形狀，但這樣的結構並不便於檢索。

在20世紀上半葉，隨著新發現的化合物及其商業用途的快速增長，組織、搜索和比較分子的問題變得至關重要：例如，當一家製藥公司試圖為一種新藥申請專利時，專利局必須核實以前是否有類似的化合物被存入。

為了應對這一挑戰，20世紀40年代引入了幾個分子索引系統，為後來被稱為化學信息學的新學科奠定了基礎。其中一個系統以作者Gordon、Kendall和Davison的名字命名為「GKD化學密碼」，由英國輪胎公司Dunlop開發，用於早期基於打卡的計算機。從本質上講，GKD密碼是一種將分子結構解析為一個字元串的算法，可以更容易地被人類或計算機查詢。

但GKD密碼和其他相關方法遠遠不能令人滿意。在化合物中，類似的結構往往會導致類似的屬性，化學家們被訓練成具有發現這種相似性的直覺，並在比較化合物時尋找它們。

例如，苯環與氣味特性的聯繫是19世紀「芳香族化合物」這一化學類別命名的原因。

另一方面，當一個分子被表示為一個字元串時（如在GKD密碼中），單一化學結構的成分可能被映射到密碼的不同位置。因此，兩個含有類似子結構的分子（因此可能具有類似的性質）可能以非常不同的方式被編碼。

這種認識促進了「拓撲密碼」的發展，研究者試圖拆解分子的結構。這方面的第一項工作是在陶氏化學公司和美國專利局完成的，它們都是化學數據庫的大用戶。

其中一個最有名的描述符，被稱為「摩根指紋」，是由Harry Morgan在化學文摘社開發的，並一直使用到今天。

出生於羅馬尼亞的蘇聯研究員George Vldu在開發早期的「結構化」方法搜索化學數據庫方面發揮了關鍵作用。

他是一名化學家，於1952年在莫斯科門捷列夫學院通過了有機化學的博士論文答辯，在大一的時候，他經歷了一次與巨大的Beilstein手冊的慘痛交鋒，使得他的研究興趣轉向化學信息學，並在這一領域工作了一輩子。

Vldu被認為是使用圖論對化合物的結構和反應進行建模的先驅者之一。從某種意義上說，這並不令人驚訝：圖論在歷史上一直與化學聯繫在一起，甚至「圖」這個詞（指一組節點和邊，而不是一個函數圖）也是由數學家James Sylvester在1878年提出的，作為化學分子的一個數學抽象。

而且Vldu主張將分子結構比較表述為圖的同構問題；他最著名的工作是將化學反應分類為反應物和產物分子的部分同構（最大公共子圖）。

Vldu的工作啟發了一對年輕的研究人員，Boris Weisfeiler（代數幾何學家）和Andrey Lehman（自稱是程序員）。

在一篇經典的合作論文中，兩人介紹了一種疊代算法，用於測試一對圖形是否同構（即，在節點重新排序之前，圖形具有相同的結構），也被稱為Weisfeiler-Lehman（WL）測試。雖然兩人在學生時代就相識，但他們的文章發表後不久就分道揚鑣了，各自在不同的領域都有了成就。

Weisfeiler和Lehman最初的猜想，即他們的算法解決了圖的同構問題（而且是在多項式時間內解決）是不正確的：雖然Lehman在計算上證明了最多有九個節點的圖，但一年後發現了一個更大的反例，事實上，一個未能通過WL測試的強規則圖被稱為Shrinkhande圖，甚至更早之前就已經被發現了。

Weisfeiler和Lehman的論文已經成為理解圖同構性的基礎。要從歷史的角度來看待他們的工作，我們應該記住，在20世紀60年代，複雜性理論仍處於萌芽狀態，算法圖理論也只是邁出了第一步。

他們的成果激發了許多後續工作，包括高維圖同構測試。在圖神經網絡領域，Weisfeiler和Lehman已經成為非常著名的人物，證明了他們的圖同構測試與消息傳遞的等價性。

儘管化學家使用類似GNN的算法已經有幾十年了，但他們關於分子表徵的工作很可能在機器學習界仍然幾乎無人知曉。我們發現很難準確地指出圖神經網絡的概念是什麼時候開始出現的：可能是因為大多數早期的工作並沒有把圖作為「一等公民」，圖神經網絡在2010年代末才開始實用，也可能是因為這個領域是從幾個相鄰的研究領域的匯合處出現的。

圖神經網絡的早期形式至少可以追溯到20世紀90年代，包括Alessandro Sperduti的Labeling RAAM, Christoph Goller和Andreas Küchler的「通過結構的反向傳播」，以及數據結構的自適應處理。

雖然這些作品主要關注對「結構」（通常是樹或有向無環圖）的操作，但其架構中保留的許多不變性讓人想起今天更常用的GNNs。

對通用圖結構處理的第一次處理，以及「圖神經網絡」這一術語的創造，發生在2000年以後，由Marco Gori和Franco Scarselli領導的錫耶納大學團隊提出了第一個GNN。他們依靠遞歸機制，要求神經網絡參數指定收縮映射，從而通過搜索固定點來計算節點表徵，這本身就需要一種特殊形式的反向傳播，而且完全不依賴節點特徵。

上述所有問題都被Yujia Li的Gated GNN（GGNN）模型所糾正，包括許多現代RNN的機制，如門控機制和通過時間的反向傳播。

Alessio Micheli在同一時期提出的圖的神經網絡（NN4G）[37]使用了前饋而非遞歸的架構，事實上更類似於現代的GNNs。

另一類重要的圖神經網絡，通常被稱之為譜（spectral），是由Joan Bruna和合作者利用圖傅里葉變換的概念而產生的。這種構造的根源在於信號處理和計算諧波分析，在2000年代末和2010年代初，處理非歐幾里得信號已經成為新趨勢。

來自Pierre Vandergheynst和José Moura小組的有影響力的論文普及了圖信號處理（GSP）的概念和基於圖鄰接和拉普拉斯矩陣特徵向量的傅里葉變換的概括。

Michal Defferrard和Thomas Kipf和Max Welling的圖卷積神經網絡依賴於頻譜濾波器，是該領域中被引用最多的。

回歸化學原點

有點諷刺的是，現代GNN被David Duvenaud作為手工製作的摩根分子指紋的替代品，以及Justin Gilmer以相當於Weisfeiler-Lehman測試的消息傳遞神經網絡的形式，成功地重新引入了它們所起源的化學領域，五十年後，這個圈子終於又閉環了。

圖譜神經網絡現在是化學領域的一個標準工具，並且已經在藥物發現和設計管道中看到使用。2020年，基於GNN的新型抗生素化合物的發現成為劃時代的成果。

DeepMind的AlphaFold 2使用了等值注意（GNN的一種形式，考慮了原子坐標的連續對稱性），以解決結構生物學的明珠——蛋白質摺疊問題。

1999年，Andrey Lehman在給一位數學家同事的信中說，他很高興得知Weisfeiler-Leman被人所知，並且仍然能夠吸引人們的研究興趣。

他沒有活著看到基於他五十年前的工作GNNs的崛起，George Vldu也沒有看到他的想法的實現，其中許多想法在他的一生中仍然停留在紙上。

我們相信，他們一定會為站在這個新的激動人心的領域的源頭而感到自豪。

Reference

\cite{bronsteinGeometricDeepLearning2017} - starting article

\cite{bronsteinGeometricDeep2021}

[deephubGeometryFoundation2021] - Chinese version of 2017

\cite{bronsteinGeometricDeep2022} - Medium blog

\cite{bronsteinGeometricDeep2022a}

\cite{bronsteinGeometricDeep2022b}

https://mbd.baidu.com/newspage/data/landingsuper?rs=994842308&ruk=xed99He2cfyczAP3Jws7PQ&isBdboxFrom=1&pageType=1&urlext=%7B%22cuid%22%3A%22_uvHu_aZHflgi2izla2wal83SilcuH8ug8SPf_aZHaKw0qqSB%22%7D&context=%7B%22nid%22%3A%22news_8603146323391492070%22,%22sourceFrom%22%3A%22bjh%22%7D

https://towardsdatascience.com/towards-geometric-deep-learning-i-on-the-shoulders-of-giants-726c205860f5

https://arxiv.org/pdf/1611.08097.pdf