Takeaway
Sequence network of variable length 例如 RNN, Transformer 適合用 layer normalization. CNN networks of fixed size 適合用 batch normalization.
Background
在深度學習神經網絡中,層與層相互之間是存在直接或間接影響的,某一層的微小變動就可能導致其他層的“劇烈震盪”,導致相應網絡層落入飽和區【sigma函數中當x<-6或x>6時,梯度值接近0,BP過程中低層神經網絡梯度消失】,導致模型的訓練困難,這種現象稱爲“Internal Covariate Shift”。爲了減小這種層與層之間的影響,學者們考慮從直觀的數據分佈**上進行處理,將批量數據標準化到~N(0,1)分佈,使得每層的輸入數據分佈範圍可控。

Batch Normalization
概念
Batch Normalization,批量歸一化 ,簡記爲BN,它在神經網絡中是一種特殊的層,一般BN位於激活函數層之前。
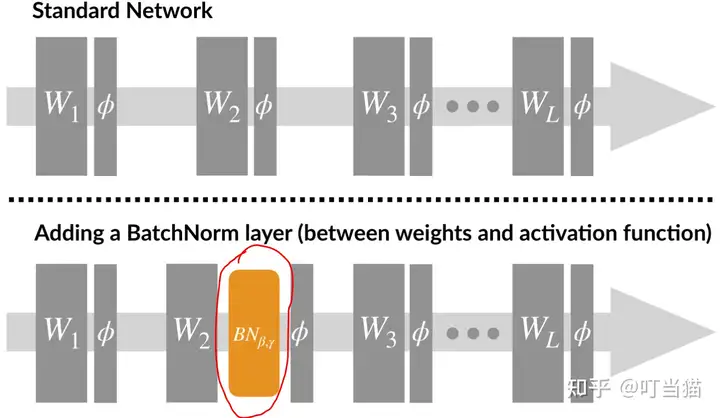
設batch_size爲m,網絡在前向傳播時,網絡中每個神經元都有m個輸出,BN就是將每個神經元的m個輸出進行歸一化處理,計算式如下:
\[\begin{aligned} & \text { Input: Values of } x \text { over a mini-batch: } \mathcal{B}=\left\{x_{1 \ldots m}\right\} ; \\ & \text { Parameters to be learned: } \gamma, \beta \\ & \text { Output: }\left\{y_i=\mathrm{BN}_{\gamma, \beta}\left(x_i\right)\right\} \\ & \mu_{\mathcal{B}} \leftarrow \frac{1}{m} \sum_{i=1}^m x_i \quad \text { // mini-batch mean } \\ & \sigma_{\mathcal{B}}^2 \leftarrow \frac{1}{m} \sum_{i=1}^m\left(x_i-\mu_{\mathcal{B}}\right)^2 \quad \text { // mini-batch variance } \\ & \widehat{x}_i \leftarrow \frac{x_i-\mu_{\mathcal{B}}}{\sqrt{\sigma_{\mathcal{B}}^2+\epsilon}} \quad \quad \text { // normalize } \\ & y_i \leftarrow \gamma \widehat{x}_i+\beta \equiv \mathrm{BN}_{\gamma, \beta}\left(x_i\right) \quad \text { // scale and shift } \end{aligned}\]以上過程包含兩步:
- **標準化:獲得0均值方差爲1的標準正態分佈 $x_i$ ;
- 尺度變換和偏移:獲得新的分佈 yi 。均值和方差分別爲 β 和 γ 【 β (偏移)和 γ (尺度變換系數)爲待學習參數】。
爲什麼要進行scale and shift過程呢?
當然,可以去掉上面的尺度變換和偏移過程,但網絡表達能力會下降。而加入該過程,有利於數據分佈和權重的互相協調。
特別地,令 γ =1, β =0等價於只有標準化過程;令 γ = σ , β = μ 等價於沒有添加BN層,而尺度變換和偏移過程包含了上面兩種特殊情況,在訓練過程中決定什麼樣的分佈比較合適,故使用尺度變換和偏移過程增強了網絡的表達能力。
綜上,無論 xi 原先的均值和方差是多少,經過BN處理後的均值和方差變爲待學習的 γ 和 β 參數。
BN的訓練和預測階段
BN在訓練和推理的時候是不一樣的。主要表現在訓練階段的batch_size>1,而預測階段的batch_size=1。
預測階段,所有參數取值是固定的,對BN層而言,意味着 μ , σ , γ , β 都是固定值。 γ , β 是訓練完成時的值。而 μ , σ 由於輸入數據只有一條,所以採用**每個批次訓練數據在網絡中每一層的均值與方差來進行無偏估計【訓練過程中需保存每一層的不同批次下產生的均值和方差數據】。
小結
BN把每層神經網絡任意神經元這個輸入值的分佈強行拉回到均值爲0方差爲1的標準正態分佈,其實就是把越來越偏的分佈強制拉回比較標準的分佈。這樣讓梯度變大,避免梯度消失問題產生,而且梯度變大意味着學習收斂速度快,能大大加快訓練速度。經過BN後,目前大部分Activation的值落入非線性函數的線性區內,其對應的導數遠離導數飽和區,這樣來加速訓練收斂過程。
Layer Normalization
BN雖然可以大大提升深度學習神經網絡的訓練速度,但是BN的缺點也是很明顯的,比如:
- 很依賴batch size的大小;
- 對神經網絡中的初始化參數敏感;
- 對於序列數據模型的效果不佳,序列不定長問題;
- Barch Normalization很難應用於在線學習模型,以及小mini-batch的分佈式模型;
- 訓練預測的計算不一致問題。
因此,針對上述BN的缺陷,層歸一化Layer Normalization(簡記爲:LN)登場了。
概念
\[\mu^l=\frac{1}{H} \sum_{i=1}^H a_i^l \quad \sigma^l=\sqrt{\frac{1}{H} \sum_{i=1}^H\left(a_i^l-\mu^l\right)^2}\]其中H表示隱藏層單元數量, l 表示網絡的第 l 層,和BN不同的是,在LN下,層中所有隱藏單元共享相同的歸一化項 μ 和 σ ,不同的訓練樣本有不同的歸一化參數。
與BN不同的是,LN對batch size的大小沒有任何限制,它可以在批大小爲1的在線方式中使用。
Layer Normalized Recurrent Neural Networks
在NLP任務中,對於不同的數據,通常有不同的文本長度。這在RNN中很容易處理,因爲每個時間步使用相同的權重。但是,當我們將BN應用於RNN時,我們需爲序列中的每個時間步計算並存儲單獨的統計信息。如果測試序列比任何訓練序列都要長,這是有問題的。LN對序列數據文本長度不敏感,在序列數據的所有時間步中,它只有一組增益和偏置參數共享。
\[\begin{aligned} & a^t=W_{h h} h^{t-1}+W_{x h} x^t \\ & \mathbf{h}^t=f\left[\frac{\mathbf{g}}{\sigma^t} \odot\left(\mathbf{a}^t-\mu^t\right)+\mathbf{b}\right] \quad \mu^t=\frac{1}{H} \sum_{i=1}^H a_i^t \quad \sigma^t=\sqrt{\frac{1}{H} \sum_{i=1}^H\left(a_i^t-\mu^t\right)^2} \end{aligned}\]$W_{hh}$ 是隱藏層-隱藏層參數, $W_{xh}$ 是輸入層-隱藏層參數。$b$ 和 $g$ 分別是偏置和增益參數。
總結
相同點
- 緩解Internal Covariate Shift問題;
- 緩解深度學習神經網絡中的梯度消失/爆炸問題;
- 加速訓練;
- 模型的正則化效果;
不同點
- BN並不適用於RNN、LSTM、Transformer等序列網絡,不適用於文本長度不定和batchsize較小的情況;而LN適合RNN、LSTM、Transformer網絡,支持文本長度不定以及batch size較小或 爲1的情況。
- BN的訓練與預測的參數計算不一致,預測過程中的均值和方差用到的是訓練過程中保存的均值和方差的平均值;LN的訓練與預測過程的計算一致。
- LN添加到CNN之後會破壞 CNN 學習到的特徵,模型無法收斂;CNN中使用BN是一個更好的選擇。BN已經成爲幾乎所有 CNN 的標配技巧了。
- LN對RNN效果更好。
- BN是對不同數據的同一個特徵進行歸一化【 batch 歸一化】;LN是對相同數據不同特徵進行歸一化【 feature 歸一化】。
在BN和LN都能使用的場景中,BN的效果一般優於LN,原因是基於不同數據,同一特徵得到的歸一化特徵更不容易損失信息。
Reference
- 知乎 https://zhuanlan.zhihu.com/p/452827651