LLM App - Lang Chain
Source
Flash Attention
Source
Optimization - NN Optimization
Source
-
https://www.ruder.io/optimizing-gradient-descent/ [@ruderOverviewGradient2016]
Introduction
神經網絡是非凸函數,因此 optimization 理論上困難。不過我們一般還是利用凸函數優化的方法用於神經網絡。
Stochastic Method
我們把原來的問題重新 formulate to fit 常見的機器學習優化問題。
原始的問題: $\min_x L(x)$, $x \in \R^n$
在機器學習中,我們有 N 個 labeled data. Loss function 改成 $L(x) = \frac{1}{N}\Sigma_{i=1}^N f_i(x)$
$f_i(x)$ 可以是 regression loss function (L2 norm or logistic regression function), classification function (entropy function)。基本都是凸函數。
$\min_x L(x) = \min \frac{1}{N} \sum^N_{i=1} f_i(x) = \min_x \sum^N_{i=1} f_i(x)$, $x \in \R^n$
此處的 $N$ 是機器學習的 samples; $x$ 是 weights, $n$ 是 number of weight.
一般 N 非常大,可以是幾百萬。同時 $N \gg n$.
如果使用 GD, 每一次迭代,最低的代价也要算一次梯度。如果 N 很大的时候,算一次完整的函数梯度都费劲,这时候就可以考虑算部分函数梯度。如果這些 sample 都是 independent, 部分函數的梯度法也會收斂到完整函數的梯度法。
一階方法:Stochastic Gradient Descent (SGD)
\[\begin{aligned}x^{k+1} & =\arg \min \left\{f_{i_k}\left(x^k\right)+<\nabla f_{i_k}\left(x^k\right), x-x^k>+\frac{1}{2\alpha^k} \|x-x^k\|^2\right\} \\& =x^k-\alpha^k \nabla f_{i_k}\left(x^k\right)\end{aligned}\]此處 $i_k \in 1, \cdots, N$
Mini-batch
\[\begin{aligned}x^{k+1} & =x^k-\alpha^k \nabla f\left(x^k; x^{(i:i+n-1)}, y^{(i:i+n-1)}\right)\end{aligned}\]一個更常用的變形是 mini-batch, 也就是用多個 samples, 通常是 16/32/…/256, 計算 gradient.
SGD Variation
Momentum method
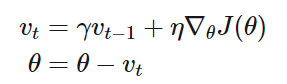
Nesterov Accelerated Gradient

Adam
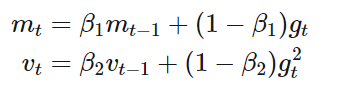
其他一系列的 stochastic GD 變形
[@gohWhyMomentum2017]
Adam, Adadelta, Adagrad, RMSProp
Netsterov, AdamW
Optimization - Manifold Gradient Descent
Source
-
https://www.youtube.com/watch?v=lK62DwSIjXA&ab_channel=FMGDataDrivenControlSummerSchool
excellent tutorial on differential geometry and manifold optimization!!
https://openreview.net/pdf?id=H1GFS4SgUS
Introduction
爲什麽要做 manifold optimization.
- 已知的 manifold, 直接在 manifold 做 optimization. 而非 use it as a constraint. 如果是 well behaved manifold. Hopefully manifold optimization 可以更有 insight.
- 如果是未知的 manifold, 也許可以用 manifold learning 先學到的 manifold. 這個 manifold 可以用於之後的 inference.
- 很多 matrix 問題 (例如 recommendation system) 其實也可以視為 manifold 問題
拜 Einstein 之賜,force,就是 gradient 也可以視爲是 curved space! 所以似乎也可以把 manifold 整合在一些 optimizer 之中。例如 https://openreview.net/pdf?id=H1GFS4SgUS
The AGM method can be seen as the proximal point method applied in this curved space.
微分幾何 (Differential geometry) 是必備的知識。幾個 key concept。
問題描述
一般歐式幾何的 optimization 問題定義如下。$S \in \mathbf{R}^n$ 而且大多是 convex set.
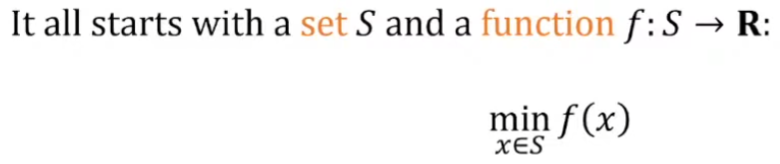
- Unconstrained optimization: $S = \mathbf{R}^n$
Manifold optimization 的描述如下。基本和一般 optimization 一樣。只是加上 manifold constraint.
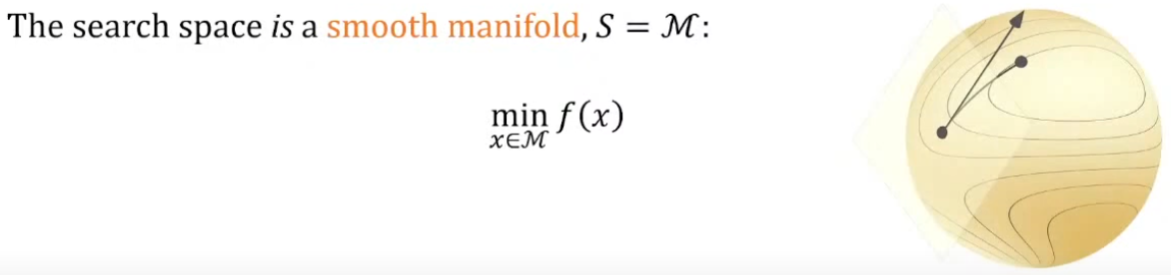
- 此處 $M$ 是 Riemannian manifold. 另外假設 $f$ 是 differentiable 存在 Riemannian gradient and Hessian.
- 更好的描述是 matrix!如下
- Rotation group 就是選擇的 operation. 很容易想像是 Remannian.
- Stiefel manifold 是 low rank 的 manifold, 常用於 recommendation system (?).
| Manifold | Matrix Representations |
|---|---|
| Stiefel manifold | $\mathcal{M}={X \in \mathbf{R}^{n \times p}: X^{T} X=I_p }$ |
| Rotation group | $\mathcal{M}={X \in \mathbf{R}^{3 \times 3} : X^{T} X=I_3 \text{ and }\operatorname{det}(X)=+1 }$ |
| Grassman manifold | $\mathcal{M}=$ {subspaces of dimension $d$ in $\mathbf{R}^n$ } |
| Fixed-rank matrices | $\mathcal{M}={X \in \mathbf{R}^{m \times n}:\operatorname{rank}(X)=r}$ |
| Positive definite matrices (convex) | $\mathcal{M}= {X \in \mathbf{R}^{n \times n}: X=X^{T} \text{ and } X \succ 0}$ |
| Hyperbolic space | $\mathcal{M}={x \in \mathbf{R}^{n+1} :x_0^2=1+x_1^2+\cdots+x_n^2}$ |
Manifold Optimization
有兩種看法
- 假設我們有 global view (也就是 global coordinate) in 歐式空間。這就回到 $x \in S$. 這和 manifold optimization 其實沒有關係。optimization 基本兩個 steps
- (Linear) gradient descent 從 $x^{k+1} = x^{k} - \alpha \nabla f$.
- Reprojection $x^{k+1}$ 到 $M$
- 微分幾何並不假設有 global coordinate, 而是只有 local coordinate. 這就無法由
- (Linear) gradient descent 從 $x^{k+1} = x^{k} - \alpha \nabla f$.
- Retraction $x^{k+1}$ 到 $M$
微分幾何 Differential Geometry Key Concept
Smooth manifold
Matrix representation
| Manifold | Matrix Representations |
|---|---|
| Stiefel manifold | $\mathcal{M}={X \in \mathbf{R}^{n \times p}: X^{T} X=I_p }$ |
| Rotation group | $\mathcal{M}={X \in \mathbf{R}^{3 \times 3} : X^{T} X=I_3 \text{ and }\operatorname{det}(X)=+1 }$ |
| Grassman manifold | $\mathcal{M}=$ {subspaces of dimension $d$ in $\mathbf{R}^n$ } |
| Fixed-rank matrices | $\mathcal{M}={X \in \mathbf{R}^{m \times n}:\operatorname{rank}(X)=r}$ |
| Positive definite matrices (convex) | $\mathcal{M}= {X \in \mathbf{R}^{n \times n}: X=X^{T} \text{ and } X \succ 0}$ |
| Hyperbolic space | $\mathcal{M}={x \in \mathbf{R}^{n+1} :x_0^2=1+x_1^2+\cdots+x_n^2}$ |
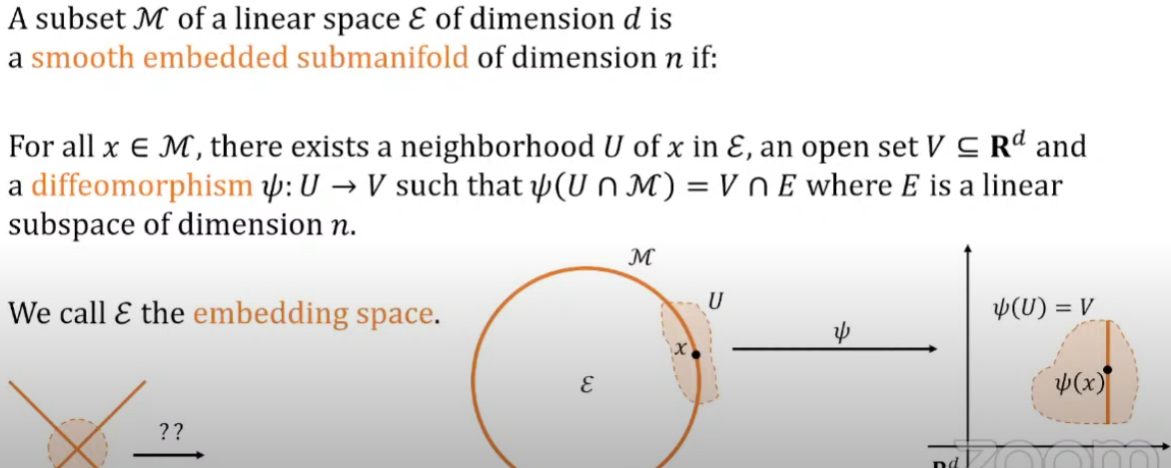
What is a manifold?
Smooth embedded sub-manifold of dimension $n$
Manifold 基本就是局部的 (平滑) 空間近似歐式 (平直) 空間。 數學的定義:$U \in \mathcal{E}$ (2D in 下圖) 是包含 $x$ 的 open set,但大於 local $\mathcal{M}$ (1D in 下圖). 存在一個 function $\psi$ 可以 map $U$ and local $\mathcal{M}$ to a flat and linear space $V$包含 $\psi(x)$.
(Smooth manifold can be linear) Tangent Space $T_xM$
- 因為 manifold 是 smooth and flat! 所以可以定義 linear tangent space
- Linear tangent space 的 dimension 和 manifold 的 dimension 相同!以下圖為例 manifold 2D; tangent pace is 2D.
- 如何找出 talent space 的 base? 利用 parameterized line! 可以找出所有 tangent vectors. $T_xM = ker Dh(x)$

Tangent Bundle $TM$
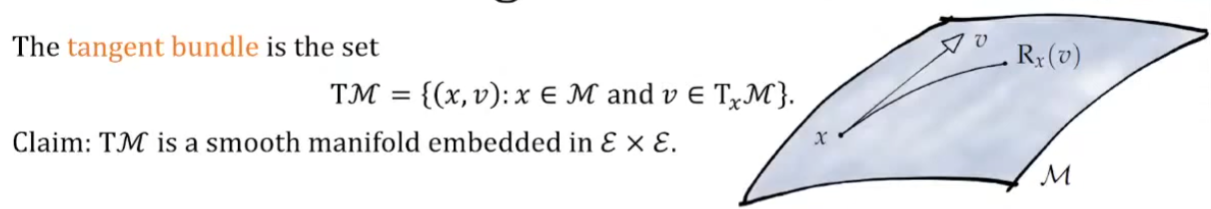
Manifold Differential

Riemannian Gradient
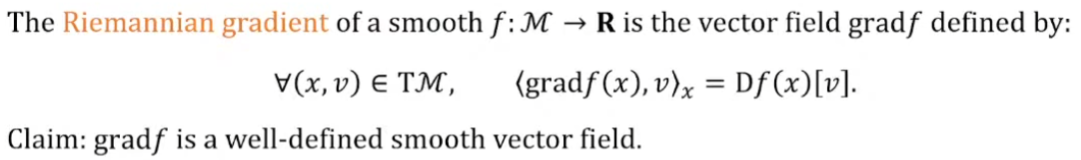

Directional derivative
Riemannian Hessian

Connection
首先在 manifold 可以定義 geodesics, 等價於歐式空間的”直線”。
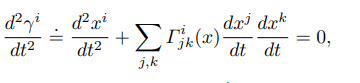
接下來可以定義 “geodesics convexity” 等價於歐式空間的 convexity.
Metric and Curvature
Manifold Optimization
基本有兩個 steps:
- Tangent space $T_p M$ 先做 gradient descent. $s_k = x_k - \alpha <grad f(x)>)$?
- Retraction
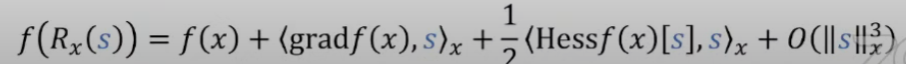
基本上 proximal gradient descent 可以視爲是 manifold gradient descent 的特例? (L2 norm regulation 可以視爲 manifold? or kernel?)
或僅是兩者的形式相同?

unconstraint convex function -> convex function + convex constraint -> convex function + manifold constrain (but not necessarily convex constraint!)
Example: Rayleigh quotient optimization
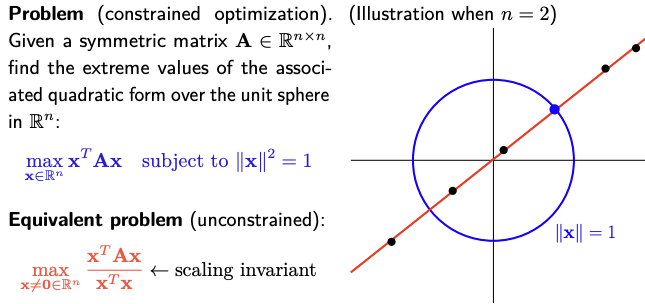
Compute the smallest (or largest) eigenvalue of a symmetric matrix $A \in \mathbf{R}^{n \times n}$ :
\[\min _{x \in \mathcal{M}} \frac{1}{2} x^{T} A x \quad \text { with } \mathcal{M}=\left\{x \in \mathbf{R}^n: x^{T} x=1\right\}\]-
注意上述問題沒有要求 $A$ 是 positive semi-definite matrix;因為有 manifold 的限制,所以 max or min 都一定存在。
-
不過正統的 Rayleigh quotient 似乎是 max。稱為 quotient 是因為除以 norm!
-
先說結論:max or min 就是最大或最小的 eigenvalues (不考慮 1/2 factor),這個結果似乎很直觀假設 $A = Q^T D Q$
-
當然對應的 $x$ 就是 Eigenvectors.
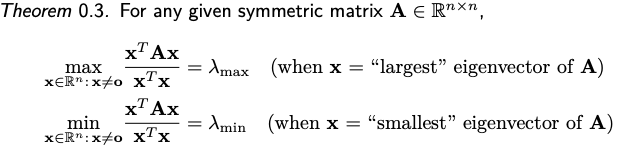
-
-
Rayleigh quotient 問題很自然可以轉換成 manifold optimization. 只要把球面 constraint 變成 manifold.
-
The cost function $f: \mathcal{M} \rightarrow \mathbf{R}$ is the restriction of the smooth function $\bar{f}(x)=\frac{1}{2} x^{T} A x$ from $\mathbf{R}^n$ to $\mathcal{M}$.
-
Tangent spaces $\quad T_x \mathcal{M}={v \in \mathbf{R}^n: x^{T} v=0 \text{ where } x^T x = 1}$.
Make $\mathcal{M}$ into a Riemannian submanifold of $\mathbf{R}^n$ with $\langle u, v\rangle=u^{T} v$.
- Projection to $T_p M$ : $\quad \operatorname{Proj}_x(z)=z-\left(x^{T} z\right) x$.
- Gradient of (包含 1/2 factor) $\bar{f}: \quad \nabla f(x)=A x$.
- (Manifold) Gradient of $f$ : $\quad \operatorname{grad} f(x)=\operatorname{Proj}_x(\nabla \bar{f}(x))=A x-\left(x^{T} A x\right) x$.
- Differential of gradf: $\operatorname{Dgrad} f(x)[v]=A v-\left(v^{T} A x+x^{T} A v\right) x-\left(x^{T} A x\right) v$.
- Hessian of $f$ : $\operatorname{Hess} f(x)[v]=\operatorname{Proj}_x(\operatorname{Dgrad} f(x)[v])=\operatorname{Proj}_x(A v)-\left(x^{T} A x\right) v$.
Optimization - Accelerate Gradient Descent
Source
-
https://www.youtube.com/watch?v=ht-gvPFsYh4&ab_channel=HanDean CMU youtube video
-
https://distill.pub/2017/momentum/ Accelerated GD
Introduction
Gradient descent (GD) 在一般的凸函數的收斂速度是 $O(1/\epsilon)$。在非光滑凸函數只能用 Sub-gradient method, 收斂速度更慢,只有 $O(1/\epsilon^2)$!
Proximal gradient descent (PGD) 可以解決非光滑凸函數收斂慢的問題。如果非光滑凸函數的 proximal operator 很容易計算,例如 L1 norm, indicator function 等等,PGD 基本就和 GD 一樣,可以在 $O(1/\epsilon)$ 收斂,而且是非光滑凸函數!
下一個問題是否能更快?YES! 這就是 accelerated gradient descent, 或是 accelerated proximal gradient descent.
我們先説結論:accelerated gradient descent 對於光滑凸函數的收斂速度是 $O(1/\sqrt{\epsilon})$。accelerated proximal gradient descent 對於非光滑凸函數的收斂速度也是 $O(1/\sqrt{\epsilon})$。
Accelerated Gradient Descent
Gradient descent 物理上常常和小球滑到山谷的最低點類比。我們看一下 GD 的公式:
$x_{k+1} = x_k - \alpha \nabla f(x_k)$
假設每次迭代的時間都是 1 秒,$x_{k+1} - x_k$ 就是速度,$\nabla f(x)$ 相當於 (重) 力。力和速度而非加速度成正比,物理上相當於摩擦力。可以想象整個山谷都浸在水裏,水的阻力就是摩擦力,$\alpha$ 就是摩擦力的倒數。$\alpha$ 愈大,摩擦力愈小,容易 overshoot 甚至發散。反之 $\alpha$ 愈小,摩擦力愈大,收斂的速度愈慢。
Accelerated gradient descent 的公式:
$v_{k+1} = \beta v_k - \alpha\nabla f(x_k)$
$x_{k+1} = x_k + v_{k+1}$
$z_k$ 稱爲 momentum 項。因爲如果 $\beta = 1 \to \nabla f = z_{k+1} - z_k$ 類似 F = d(mv)/dt, 也就是 momentum.
$\beta=0$ 就和 GD 一樣 (over-damped)。 $\beta$ 愈接近 1 代表 momentum 愈大 (under-damped)。
此時 $\alpha$ 因爲是位置和 momentum 的比例,相當於質量而不是摩擦力的倒數。
- 在 high curvature direction, 前後 gradient 方向相反而會互相抵消,因此是 damped oscillation. $\beta$ 接近 1, 代表抵消效果越好。
- 在 low curvature direction, 前後 gradient 方向相同互相加强。可以很快收斂。 如下圖。
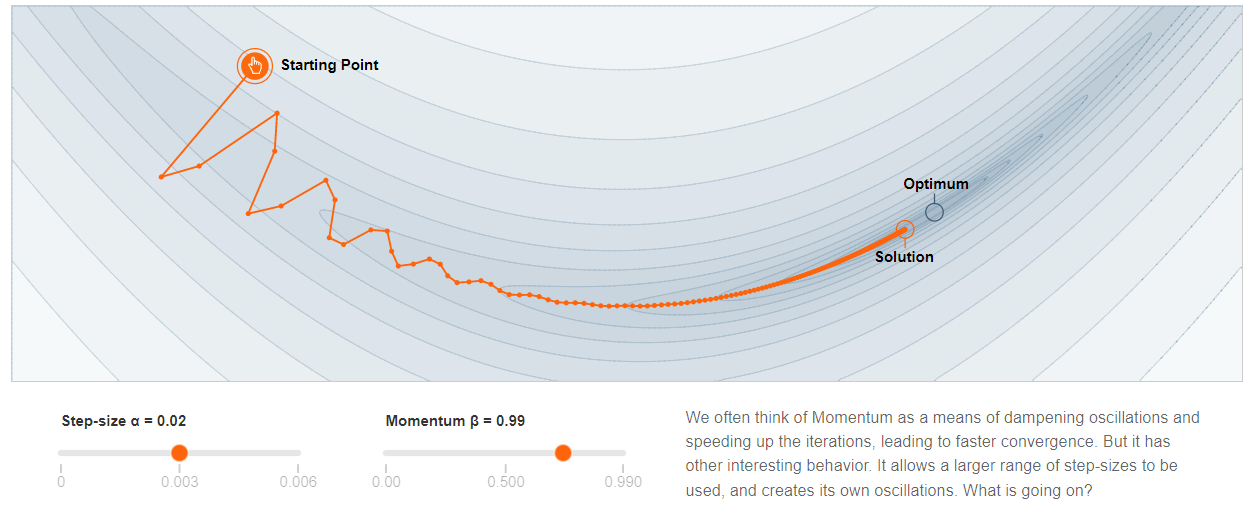
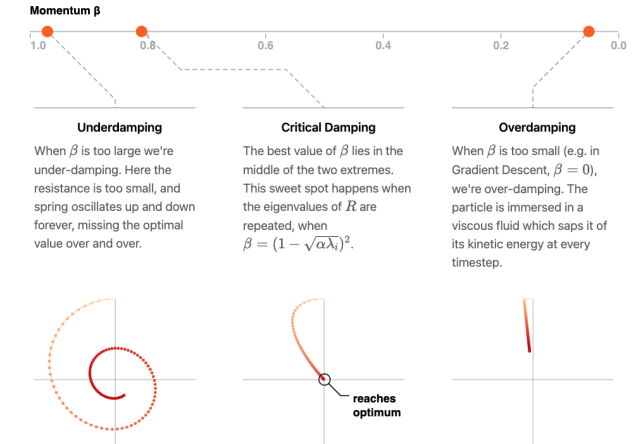
Quadratic Function
我們用 (矩陣) 二次式爲例。雖然是簡單的例子,但有物理意義。 \(f(w)=\frac{1}{2} w^T A w-b^T w, \quad w \in \mathbf{R}^n\) 此處假設 $A$ 是對稱而且可逆 (full rank) 矩 (方) 陣。因此 optimal solution $w^{\star}$ 是當 \(w^{\star}=A^{-1} b\) (Yes!) 如果要 convex, 是否需要所以 eigenvalues 都是正值? positive semi-definite?, i.e. $A \succeq 0$, 加上 invertible 所以 $A \succ 0$
Gradient Descent
因爲 $\nabla f(w)=A w-b$, GD 的迭代公式如下 \(w^{k+1}=w^k-\alpha\left(A w^k-b\right)\) 對於對稱的矩陣 $A$ 做 eigenvalue decomposition \(A=Q \operatorname{diag}\left(\lambda_1, \ldots, \lambda_n\right) Q^T, \quad Q=\left[q_1, \ldots, q_n\right]\) 另外根據習慣, $\lambda_i$ 從小排到大: $\lambda_1$ (最小) to biggest $\lambda_n$ (最大)。$Q$ 是 (幺) 正交矩陣 (orthonormal) , $q_i$ 對應新的正交基底,$\lambda_i$ 是新的 scaling factor。
再來做一個基底變換 ($w \to x$) 並扣除 bias, $x^k=Q^T\left(w^k-w^{\star}\right)$, 可以讓 GD 迭代變成每個基底 separable! 而更有物理意義! \(w^{k+1}=w^k-\alpha\left(A w^k-b\right) \\ Q^T(w^{k+1} - w^*)= Q^T(w^k - w^*) -\alpha Q^T\left(A w^k-b\right) \\ x^{k+1} = x^k - \alpha Q^T A (w^k - A^{-1} b) \\ x^{k+1} = x^k - \alpha Q^T Q D Q^T (w^k - A^{-1} b) = x^k - \alpha D x^k\) 再來拆開每個坐標軸! \(\begin{aligned} x_i^{k+1} & =x_i^k-\alpha \lambda_i x_i^k \\ & =\left(1-\alpha \lambda_i\right) x_i^k=\left(1-\alpha \lambda_i\right)^{k+1} x_i^0 \end{aligned}\) 其中 $x_i$ 對應 $q_i$ 坐標軸。
-
此時我們可以把 $\R^n$ 的優化問題變成 $n$ 個 $\R^1$ 的優化問題!
-
每個坐標軸 $q_i$ 從初始距離 $x_i^0$ 呈幾何數列 (公比 $1-\alpha \lambda_i$) 收斂到 0.
-
收斂的條件是 $\vert 1-\alpha_i \lambda_i \vert < 1$. 收斂最慢的坐標軸就決定最終的收斂速度,也就是 bottleneck.
回到原始的坐標系 $w$, 變回 $\R^n$ ($q_1, q_2, …, q_n \in \R^n$), 可以得到 GD 的 close form in $\R^n$. 不過沒有上式有物理意義! \(w^k-w^{\star}=Q x^k=\sum_i^n x_i^0\left(1-\alpha \lambda_i\right)^k q_i\)
最佳步長 $\alpha$
前面分析提供直接的 guidance 如何選取步長 $\alpha$.
-
收斂的條件是 $\left 1-\alpha \lambda_i\right < 1$, 也就是 $0<\alpha \lambda_i<2$, 似乎可以推導出 $ \to 0<\alpha < 2/\lambda_i$ 。 Yes! 因爲 convex 要求所有 $\lambda_i$ 是正數!不過假設所有 eigenvalues 都是正值而且 $\lambda_n$ 是最大 eigenvalue,$0 < \alpha < 2/\lambda_n$ - 整體收斂速度是由上式最慢的 error term 決定,也就是最接近 +1 或是 -1. 因爲 $\lambda_i$ 從小排到大: $\lambda_1$ (最小,可爲負值) to biggest $\lambda_n$ (最大)。直觀上收斂的 rate 只由最大或最小的 eigenvalue 決定! $\lambda_1$ or $\lambda_n$ :
\(\begin{aligned} \operatorname{rate}(\alpha) & =\max _i\left|1-\alpha \lambda_i\right| \\ & =\max \left\{\left|1-\alpha \lambda_1\right|,\left|1-\alpha \lambda_n\right|\right\} \end{aligned}\) 我們現在要選擇 $\alpha$ to minimize rate($\alpha$) , 就是上式!
- 如果 $\lambda_1 = \lambda_n$ 代表所有的 eigenvalues 都一樣。這是 trivial case, 只要選 $\alpha = 1/\lambda_1 = 1/\lambda_n \to \min \operatorname{rate}(\alpha) = 0$ 一步到位。
- 如果 $\lambda_1 \ne \lambda_n$. 一個自然 (但非最佳) 的選擇是 $\alpha = 1/\lambda_n \to$ $\operatorname{rate}(\alpha) = 1-\lambda_1 / \lambda_n < 1$
- 最佳的解是讓 $1-\alpha \lambda_1$ 和 $1-\alpha \lambda_n$ 在 0 兩側相等!
- $1-\alpha \lambda_1 = -(1-\alpha\lambda_n ) \to \text { optimal } \alpha=\underset{\alpha}{\operatorname{argmin}} \operatorname{rate}(\alpha) = \frac{2}{\lambda_1 + \lambda_n}$
- $\text { optimal rate }=\min _\alpha \operatorname{rate}(\alpha)=\frac{\lambda_n / \lambda_1-1}{\lambda_n / \lambda_1+1}$
- 可以看一下比較: $\lambda_n = 5 \lambda_1$, 自然解的 rate = 1 - 1/5 = 4/5; 最佳解 = (5-1)/(5+1) = 4/6 更小!
In summary \(\begin{aligned} & \text { optimal } \alpha=\underset{\alpha}{\operatorname{argmin}} \operatorname{rate}(\alpha)=\frac{2}{\lambda_1+\lambda_n} \\ & \text { optimal rate }= \gamma_{GD} = \min _\alpha \operatorname{rate}(\alpha)=\frac{\lambda_n / \lambda_1-1}{\lambda_n / \lambda_1+1} = \frac{\kappa -1}{\kappa+1} \end{aligned}\) Notice the ratio $\lambda_n / \lambda_1$ determines the convergence rate of the problem. In fact, this ratio appears often enough that we give it a name, and a symbol - the condition number. \(\text { condition number }:=\kappa:=\frac{\lambda_n}{\lambda_1}\) Question: 爲什麽不讓 $\alpha$ 從純量 (scalar) 變成向量? 就是每個 $q_i, \lambda_i$ 都有自己的 $\alpha_i$?
Decompose Error
\[\epsilon = f(w^k)- f(w^{\star}) = \sum_i^n \left(1-\alpha \lambda_i\right)^{2k} \lambda_i [x_i^0]^2\]Optimal Rate and Error Converge Rate
有兩種方式評價不同算法的效能: (1) optimal rate; (2) Error Converge Rate.
Optimal rate 就是等比級數的公比 $\gamma = \min_{\alpha} \vert 1-\alpha \lambda_i \vert = \frac{\kappa-1}{\kappa +1} < 1$ ,越小收斂越快
Error Converge Rate 則是 $\epsilon$ 和 $k$ 的關係 $k = \frac{\log \epsilon + c}{2 \log \gamma} \propto O(\log (\frac{1}{\epsilon})/\log(\frac{1}{\gamma}))$ ,越小收斂越快
- 對於 strong convex function, 才會有等比數列收斂的公比 $\gamma$ and $\log \epsilon$
- 如果是一般 convex function, 一般用 Error Converge Rate 而不用 $\gamma$
Gradient Descent 收斂速度
-
$\kappa \ge 1$
-
Optimal rate = $\gamma_{GD} = \frac{\kappa-1}{\kappa+1}$ 越小越好收斂越快
-
最容易的例子是 $\kappa=1$, 可以很快收斂。如果 $\kappa \gg 1$, 稱爲 ill-condition, GD 只能讓 $\alpha$ 變小才能收斂。這會導致收斂速度變慢。
Accelerated (Momentum) Gradient Descent
接下來我們研究 accelerated (momentum) GD 如下:
\(\begin{aligned}
z^{k+1} & =\beta z^k+\nabla f\left(w^k\right) \\
w^{k+1} & =w^k-\alpha z^{k+1}
\end{aligned}\)
二次式, $\nabla f\left(w^k\right)=A w^k-b$, 的迭代公式如下:
\(\begin{aligned}
z^{k+1} & =\beta z^k+\left(A w^k-b\right) \\
w^{k+1} & =w^k-\alpha z^{k+1} .
\end{aligned}\)
同樣我們可以做基底變換: $x^k=Q\left(w^k-w^{\star}\right)$ and $y^k=Q z^k$, 得到每個基底 separable 的迭代!
\(\begin{aligned}
& y_i^{k+1}=\beta y_i^k+\lambda_i x_i^k \\
& x_i^{k+1}=x_i^k-\alpha y_i^{k+1} .
\end{aligned}\)
注意上式每一個基底都是獨立分離的!(雖然 $x_i^k$ and $y_i^k$ are coupled). 我們把上式改寫成如下:
\(\left(\begin{array}{c}
y_i^k \\
x_i^k
\end{array}\right)=R^k\left(\begin{array}{c}
y_i^0 \\
x_i^0
\end{array}\right) \quad R=\left(\begin{array}{cc}
\beta & \lambda_i \\
-\alpha \beta & 1-\alpha \lambda_i
\end{array}\right)\)
非常有趣,accelerated GD 的物理意義是把原來 1D 的 exponential decay (等比公式),轉換成 2D (2x2 矩陣) damped oscillation!!
-
假設 2x2 矩陣 $R$ 的 eigenvalues 是 $\sigma_1$ 和 $\sigma_2$. $\vert \sigma_1 \vert, \vert \sigma_2 \vert < 1$. 這樣才可以保證收斂!
-
注意 $\sigma_1$ 和 $\sigma_2$ 不一定是實數。如果要收斂快,最好是 damped oscillation!如此 $\sigma_1, \sigma_2$ 就會是 (共軛) 複數。
-
可以得到下列公式 for $R^k$:
\(R^k=\left\{\begin{array}{ll} \sigma_1^k R_1-\sigma_2^k R_2 & \sigma_1 \neq \sigma_2 \\ \sigma_1^k\left(k R / \sigma_1-(k-1) I\right) & \sigma_1=\sigma_2 \end{array}, \quad R_j=\frac{R-\sigma_j I}{\sigma_1-\sigma_2}\right.\)
Optimal parameters $\alpha, \beta$
我們同樣可以優化 $\alpha$ and $\beta$ 得到最快的 global convergence rate。結果如下: \(\alpha=\left(\frac{2}{\sqrt{\lambda_1}+\sqrt{\lambda_n}}\right)^2 \quad \beta=\left(\frac{\sqrt{\lambda_n}-\sqrt{\lambda_1}}{\sqrt{\lambda_n}+\sqrt{\lambda_1}}\right)^2\) 將 $\alpha, \beta$ 帶入 $R$ 矩陣,可以得到 \(\gamma_{AGD} = \frac{\sqrt{\kappa}-1}{\sqrt{\kappa}+1} \begin{aligned} \end{aligned}\)
-
$\kappa \ge 1$ and $0 \le \beta < 1$
-
AGD optimal rate $\gamma_{AGD} = \frac{\sqrt{\kappa}-1}{\sqrt{\kappa}+1}$ 越小越好收斂越快。在 $\kappa \gg 1$ , 也就是 ill-condition $\gamma_{AGD} \ll \gamma_{GD} < 1$, AGD 收斂比 GD 快得多。
-
Error Converge Rate: $O(\log (\frac{1}{\epsilon})/\log(\frac{1}{\gamma_{AGD}})) < O(\log (\frac{1}{\epsilon})/\log(\frac{1}{\gamma_{GD}})) $ 因爲有 log 函數,其實好像沒有差太多。
Proximal Gradient Descent (PGD)
雖然沒有人直接用 PGD 於二次式,但看一下結果還是非常有物理意義。
From [@boydProximalAlgorithms2013]
首先二次式 \(f(w)=\frac{1}{2} w^T A w-b^T w, \quad w \in \mathbf{R}^n\)
接著
\[\begin{aligned} \operatorname{prox}_{\alpha f}\left(w^k\right)& =\underset{w}{\operatorname{argmin}}\left((1 / 2) w^T A w-b^T w+\frac{1}{2 \alpha}\left\|w-w^k\right\|_2^2\right) \\ & =(A+(1 / \alpha) I)^{-1}\left(b+(1 / \alpha) w^k\right) \end{aligned}\]利用 proximal iterative algorithm
\[\begin{aligned} w^{k+1} &=(A+(1 / \alpha) I)^{-1}\left(b+(1 / \alpha) w^k\right), \\ &=w^k+(A+\epsilon I)^{-1}\left(b-A w^k\right), \end{aligned}\]where $\epsilon = 1/\alpha$
利用 $A=Q \operatorname{diag}\left(\lambda_1, \ldots, \lambda_n\right) Q^T, \quad Q=\left[q_1, \ldots, q_n\right]$, 加上坐標變換 $x^k=Q^T\left(w^k-w^{\star}\right)$, and $w^{\star}=A^{-1} b$
\[w^{k+1}=w^k-(A+\epsilon I)^{-1}\left(A w^k-b\right) \\ Q^T(w^{k+1} - w^*)= Q^T(w^k - w^*) - Q^T (A+\epsilon I)^{-1} \left(A w^k-b\right)\\ x^{k+1} = x^k - Q^T (QDQ^T+\epsilon Q Q^T)^{-1} Q D x^k \\ x^{k+1} = x^k - (D+\epsilon I)^{-1} D x^k\]再來拆開每個坐標軸! \(\begin{aligned} x_i^{k+1} & =x_i^k-\frac{\lambda_i}{\epsilon+\lambda_i} x_i^k \\ & =\left(1-\frac{\lambda_i}{\epsilon + \lambda_i}\right) x_i^k=\left(\frac{\epsilon}{\epsilon + \lambda_i}\right)^{k+1} x_i^0 \end{aligned}\)
其中 $x_i$ 對應 $q_i$ 坐標軸。
- 可以看到 $x^k$ 也會等比數列收斂到 0! 因爲 $\frac{\epsilon}{\epsilon + \lambda_i} < 1$. 但是和 GD 的方式不同 $(1-\alpha \lambda_i)<1$.
-
如果 $\epsilon \gg \lambda_i \to (1-\frac{\lambda_i}{\epsilon+\lambda_i}) \approx (1-\epsilon^{-1}\lambda_i) = (1-\alpha \lambda_i)$ 基本就是 gradient descent.
- PGD 的好處: 如果 $A$ 有 high condition number $\kappa \gg 1$, 也就是 ill-condition, 一般 GD 收斂非常慢或是計算 $A^{-1}$ 也不容易算精確。但是加上 $(A + \epsilon I)^{-1}$ 稱爲 regularized matrix 則沒有計算精確的問題 (always positive definite)!
Advanced Optimization with Adaptive Step (不僅僅用於二次式)
二次式是簡單的 case, 因為二次微分 (Hessian) 為定值。因此步長 $\alpha$ (以及 momentum when $\beta \approx 1$ ) 可以 (也只需要) 是定值。
對於一般複雜的非二次式,我們不知道二次微分導數 (Hessian)。通常二次導數也非定值,所以需要用 adaptive 方法估計步長 $\alpha$(and $\beta$?)才能快速收斂。
我們再看深度學習中更常用的加速算法。

我們先用直觀方法。SGD 基本類似 GD ($x_{k+1} = x_k - \alpha_k \nabla f(x_k)$ )。有兩個原則決定 $\alpha_k$
- $\alpha_k$ 應該開始比較大以加速收斂,隨著$k$ 越大會越小以得到好的準確度。
- $\alpha_k$ 應該和 $f(x_k)$ 的二次微分 (Hessian) 成反比。二次微分小,代表比較平直,$\alpha_k$ 可以比較大,反之則比較小。
- 利用二階牛頓法 ($x_{k+1} = x_k - H^{-1} \nabla f(x_k)$). 如何近似 $H(x_k)$? 利用 Fisher information: $H(x_k) \approx \nabla f(x_k)^2$
- 要估計 2nd order 倒數有困難。可以利用 Fisher information!! 2nd order derivative ~ (-1) * (1st order derivative)^2
我們看 AdaGrad 就是 $v_t = \sum_{i=1}^t g_i^2$ and $x_{t+1} = x_t - \frac{\alpha_t}{ \sqrt{v_t}} g_t$
AdaGrad 有兩個缺點
- Learning rate 會不斷變小,因為 $g_i^2$ 會越來越小。這會造成學不到新的東西
- 沒有 momentum 加速!
改善 1. 只要加入 momentum term 即可。AdaForm
改善 2. 利用 exponential weight of $g_t$, 讓新的 $g_t$ 佔的 weight 比較小。AMSGrad or RMSProp
同時改善 1 and 2. 就變成 Adam!
其中 $g_t$ 代表 gradient. $m_t$ 代表 exponentially weighted gradient estimate. 主要是多了一項 $(1-\beta)$ 讓 gradient 佔的比例變小。
另外多了一項 $v_t$, 可以視為 normalized $\alpha$? $\alpha_t/\sqrt{v_t}$ 稱為 effective stepsize.

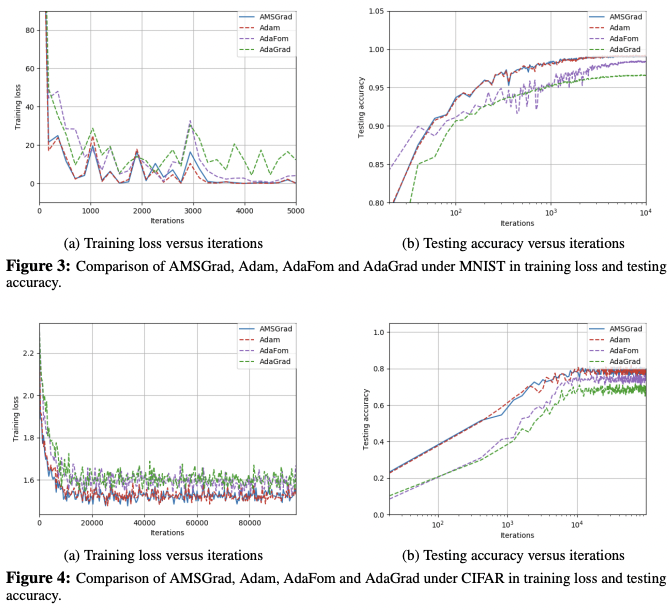
Convex Function with L1 Regularization
因爲 L1 regularization 是非光滑函數。需要使用 Proximal algorithm.
如果使用 (sub)-gradient descent ,

Accelerated PGD


可以看到 L1 regularization 的 proximal gradient descent algorithm 稱爲 ISTA (Iterative Soft-Thresholding Algorithm) 和 gradient descent 主要的差異是多加了 soft-thresholding. 加上 soft-thresholding 的收斂速度和 GD 也就差不多。
顯然這不是最快收斂的算法,還可以再 accelerate! 就是 FISTA (Fast ISTA) for L1 regularization. FISTA 和 ISTA 的差異就是引入 momentum $v$. In general accelerated proximal gradient method 和 accelerated GD 主要的差異是多加 prox operator.
對於強凸函數 (e.g. quadratic function) with (非光滑) L1 regularization.
-
(Sub)-gradient descent Error Converge Rate: $O(1/\epsilon^2)$
-
Proximal gradient Error Converge Rate: $O(\log (\frac{1}{\epsilon})/\log(\frac{1}{\gamma_{GD}}))$
-
Accelerated proximal gradient Error Converge Rate: $O(\log (\frac{1}{\epsilon})/\log(\frac{1}{\gamma_{AGD}}))$
對於一般光滑凸函數 + 非光滑 proximal friendly 函數。
- (Sub)-gradient descent Error Converge Rate: $O(1/\epsilon^2)$,如下圖黑綫
- Proximal gradient Error Converge Rate: $O(1/{\epsilon})$ ,如下圖紅綫
- Accelerated proximal gradient Error Converge Rate: $O(1/{\sqrt{\epsilon}})$ ,如上面公式,如下圖紫綫 (?)
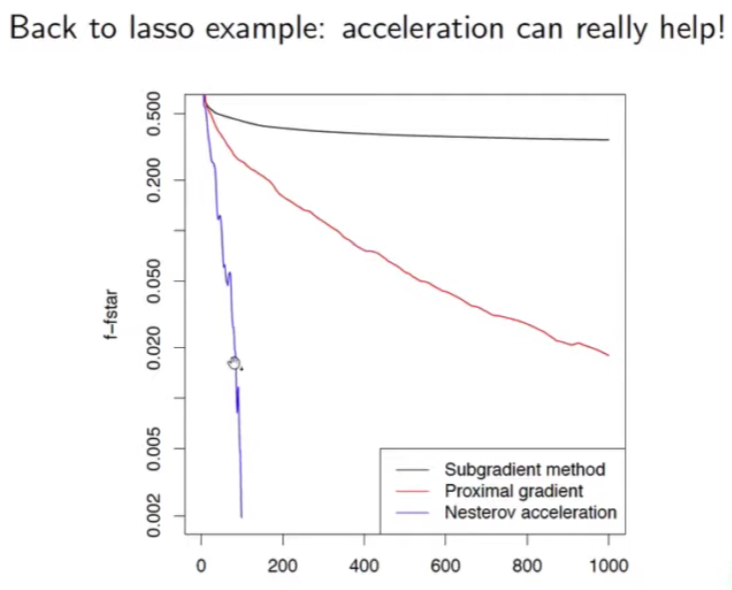
Optimization - Proxmial Gradient Descent
Source
-
非線性優化方法的總結: https://zhuanlan.zhihu.com/p/85423364?utm_id=0 很好的總結文章
-
Stanford: Proximal Algorithms [@boydProximalAlgorithms2013]
Introduction
(Convex) optimization 的問題之一是不可微分,如下圖 1D 最小值點不可微分。
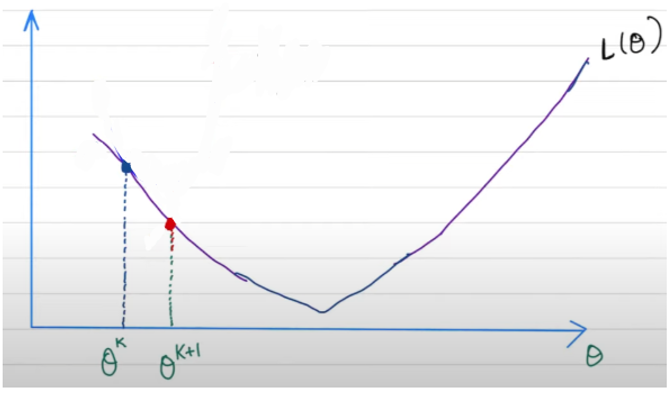
或是如下圖 2D $\min_x f(x) = |Aw+b|^2 + \lambda \vert w \vert$, 此處 $w = (w_1, w_2)$
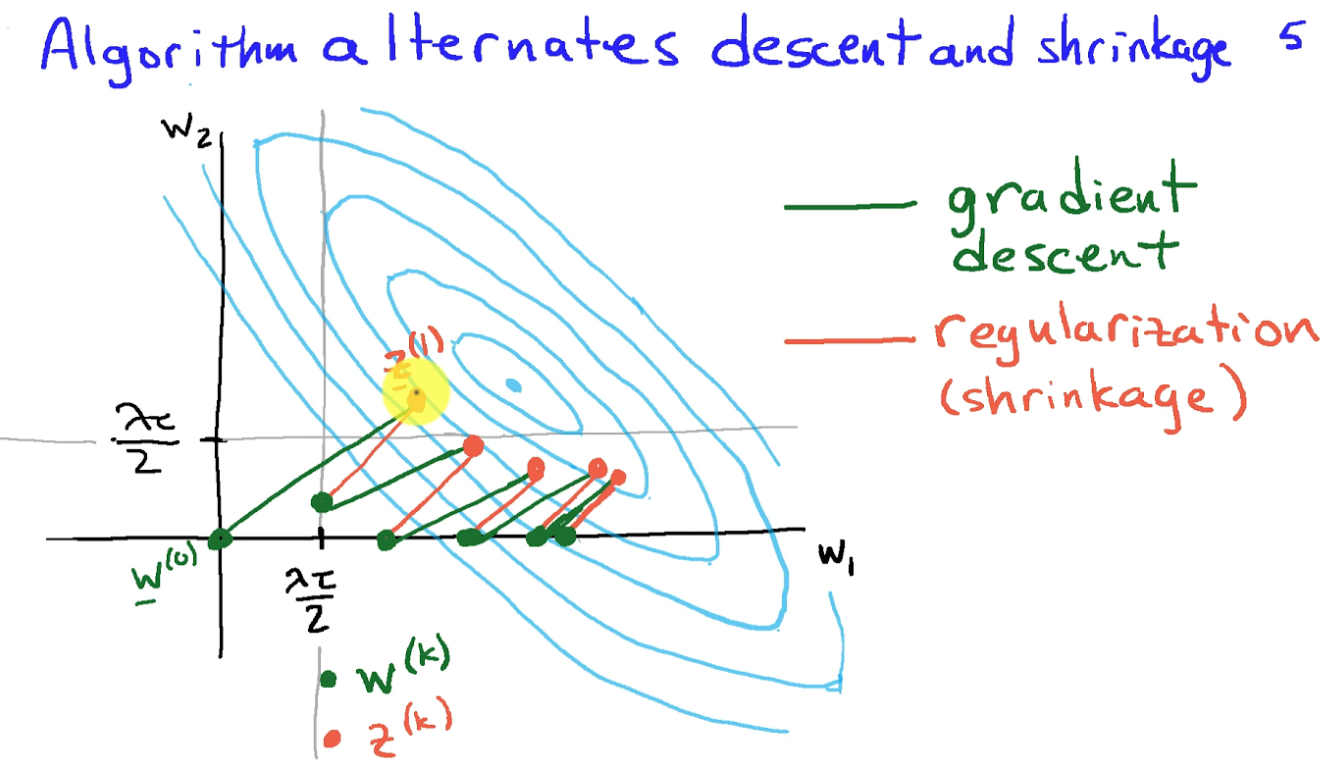
傳統的 gradient descent (需要一階微分) 或是 Newton method (需要一階和二階微分) 在基本無法收斂!
如何解決不可微分問題?
一個方法是 sub-gradient descent, 就是每次疊代減小 learning rate ($\alpha \to \alpha_k$), \(x_{k+1} = x_k - \alpha_k \partial f(x_k)\) 雖然可行,但是收斂速度太慢。更好的方法是 proximal gradient descent.
光滑化有兩種方式:
- Conjugate function: 把不可微分的函數變成可微分共軛函數。
非光滑凸函數優化問題
- 如果 $f(x)$ 是 $\beta$ smooth function, 直接用 GD 即可。只是要選一個適當的 $\alpha < \beta$.
- 會有問題就是非光滑函數。我們就把這些函數分開 $f(x) + g(x)$ 其中 $f(x)$ 是光滑函數, $g(x)$ 是非光滑函數 (一般有限非光滑點)。
考慮一般非光滑問題:
\[\min_x f(x) + g(x)\]其中 $f(x)$ 是 smooth function. $g(x)$ 包含非 smooth 點。最常見非光滑 (凸) 函數的就是 L1 norm 和 indicator function (0 in the constraint domain, $\infty$ otherwise), and L$\infty$ norm (max). L1 norm 很容易理解。Indicator function 常用於 constraint domain case. 就是把 constrain 轉換成 function.
Proximal Gradient Descent 結論
先說結論
$x_{k+1} = \arg \min_x {f(x_k) + \nabla f(x_k)(x-x_k) + \frac{1}{2\alpha_k}(x-x_k)^2 + g(x)} = prox_{\alpha_k g}(x_k - \alpha_k \nabla f(x_k)) $
PGD 可以視爲分成兩步
Step 1: 在光滑的 $f(x)$ 執行標準的 Gradient Descent: $z_k = x_k - \alpha_k \nabla f(x_k)$
Step 2: 在非光滑 (但 proximal friendly) 的 $g(x)$ 執行 proximal operation: $x_{k+1} = prox_{\alpha_k g} (z_k)$
下一個問題是什麼是 proximal operation? 可以參考 Stanford 的 paper [@boydProximalAlgorithms2013]
PGD 常見的説法
- 假如 $g(x)$ 是 L1-norm, $f(x) + g(x)$ 稱爲 Lasso regularization. Proximal operation of L1 norm 對應一個 backward operation (見下圖紅線). 所以 PGD 有時稱爲 forward (GD, 下圖綠綫)-backward (L1 regularization, 下圖紅線) algorithm.

- 假如 $g(x)$ 是 indicator function (0 in the constraint domain, $\infty$ otherwise) 情況下, proximal operation 可以視爲 projection operation. 如果 GD 把 $z_k$ 移動出 constraint domain, proximal operation 再把 $z_k$ 投影回 constraint domain as $x_{k+1}$ .
Proximal Operator and Moreau Envelope Function
Proximal operator 和 Moreau envelope function 就是解決不可微分 (non-smooth) 的問題。
從值域 (Moreau envelope function)
先定義 Moreau envelope function 如下:
$M_{\gamma g}(x) = \inf_{z} \left{ g(z) + \frac{1}{2\gamma}(x-z)^2\right} \le g(x)$
$g(x) +\frac{1}{2\gamma}(x-x_k)^2 \ge g(x) \ge M_{\gamma g}(x)$.
- Moreau envelope function $M_{\gamma g}(x)$ 永遠小於等於原來函數。是原來函數的光滑下界。如下圖虛線。
- Morean function 的最小值等於原來函數的最小值。
- 如果 $g(x)$ 是 convex function, Moreau function 也是 convex function
- Moreau function 是否可微分? Yes! It’s always Frechet differentiable, with its gradient being 1-Lipschtz continuous. 也就是 smooth! 但並非 strongly convex!
- 上式最左項是 $g(x)$ 加上一個正值的上界,也就是類似 Moreau 但沒有 $\inf$。如下圖的灰綫。
從定義域 (Proximal Operator)
Proximal 是 operator $\R^n \to \R^n$, 而不是 function $\R^n \to \R$.
Proximal operator 的定義如下: \(\begin{aligned} \operatorname{prox}_{\gamma g}(x) & =\arg \min _z\left\{g(z)+\frac{1}{2 \gamma}(z-x)^2\right\} \end{aligned}\) 很難直接看出 proximal operator 的定義!特別是 operator 而不是 function.
Moreau envelope (or Moreau-Yosida regularization) function 和 proximal operator 有非常密切的關係,如下式。(How to prove?)
下式看起來非常像 gradient descent, 只是 $g(x) \to M_{\gamma g}(x)$, 就是下界函數。
如果沒有 gradient, 就換成 sub-differential. 不過 Moreau 應該 smooth, 所以 gradient 應該存在?
\(\begin{aligned}
&\operatorname{prox}_{\gamma g}(x)=x-\gamma \nabla M_{\gamma g}(x) \\
& \operatorname{prox}_{\gamma g}(x)=x-\gamma \partial M_{\gamma g}(x)\end{aligned}\)
一個得到 prox operator 的方法就是從 Moreau envelope function 計算 GD 得出。一般不會這樣操作。
Example
例一: $f(z)$ 是光滑 function 假設 $f(z) \approx f(x) + (z-x) \nabla f + \frac{1}{2}(z-x)^2 \nabla^2 f +…$ \(\begin{aligned} \nabla f + (\nabla^2 f +\frac{1}{\gamma}) (z-x) = 0 \to z = prox_f(x) = x - \frac{\gamma}{1+\gamma \nabla^2 f} \nabla f \end{aligned}\)
- 如果 $\gamma \nabla ^2 f \ll 1$, 也就是Hessian 遠小於 1/$\gamma$, Proximal operator 基本就化簡為 gradient descent.
例二: $\gamma \to +\infty$ (sanity check) \(\begin{aligned}\operatorname{prox}_{\gamma f}(x) & \approx \arg \min _z\left\{f(z)\right\} = x_{min}\end{aligned}\)
\[\begin{aligned}M_{\gamma f}(x) & \approx f_{min}\end{aligned}\]- 此時 prox operator 不論 input $x$ 是什麼,都輸出 $x_{min} \in \R^n$.
-
Moreau function 同樣不論 input $x$ 輸出 $ f_{min}$.
- 因爲 Moreau function 是常數,其 gradient 為 0。$\gamma \to \infty$ 所以兩者抵消。
例三: $\gamma \to 0$ (sanity check) \(\begin{aligned}\operatorname{prox}_{\gamma f}(x) & \approx \arg \min _z\left\{\|z-x\|^2 \right\} = x\end{aligned}\)
\[\begin{aligned}M_{\gamma f}(x) & \approx f(x)\end{aligned}\]- 此時 prox operator 和 Moreau function 基本可以忽略。
Proximal operator 物理意義
控制 $\gamma$ from 0 to 無限大,可以看到 $prox_f(x)$ 從 $x$ 逼近 $x_{min}$. 在 $\gamma = 1$ 基本就是 $x$ 和 $x_{min}$ 之間!也就是 $x$ 被拉近到 $x_{min}$ 的位置!
也可以從這個公式看出:
\(\begin{aligned}&\operatorname{prox}_{\gamma f}(x)=x-\gamma \nabla M_{f\gamma}(x) \\& \operatorname{prox}_{\gamma f}(x)=x-\gamma \partial M_{\gamma f}(x)\end{aligned}\)
$\gamma$ 越大,$x$ 就移動越靠近 $x_{min}$.
我們看實際的例子:
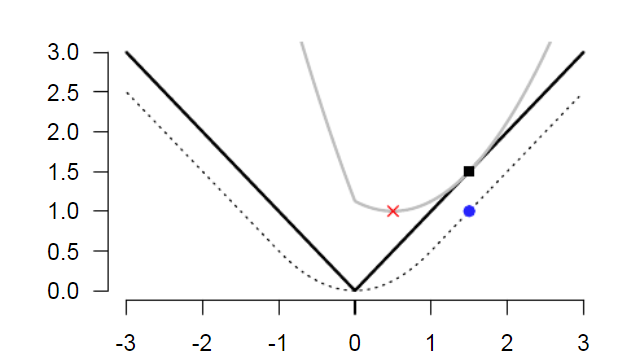
例四: $f(x) = \vert x \vert$
-
$f(x)$ 如下圖實心黑線。
-
$f(x)$ 的 Moreau function $M_f(x)$ 如下。物理意義是 Huber function,是一個下界可微分函數。
-
假設 $\gamma = 1$, Moreau function 就是下圖虛線。
-
灰色的實線對應 $\vert x \vert + (1/2)(x-x_0)^2$ for $x_0=1.5$. 其 minimum 是紅點位置。
- 對應的 $x=0.5$ 就是 1-D proximal operator output: $prox_f(1.5)=0.5$
- 對應的 $y = 1$ 就是 Moreau function: $M_f(1.5) = 1$

以上例 $f(x) = \vert x \vert$ , L1-norm 來看
-
$prox_f(1.5) = 1.5 - 1 = 0.5$!
-
$prox_f(1) = 1 - 1 = 0$
-
$prox_f(0.5) = 0.5 - 0.5 = 0$
-
$prox_f(0) = 0 - 0 = 0$ (minimum!) \(prox_{\gamma f}(x) = x - \gamma \nabla M_{\gamma f}= \begin{cases} x-\gamma, & x > \gamma, \\ 0, & \vert x \vert \le \gamma , \\ x+\gamma, & x < -\gamma .\end{cases}\)
-
如果用 $x_{k+1} = prox(x_k)$ 最後可以疊代出 $x_{i} \to 0$, 也就是 $x_{min}$ 得到 $f(x)$ 的極小值。
例五
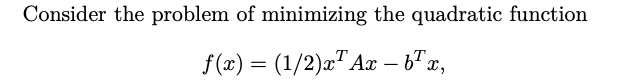
Where A is semidefinite.
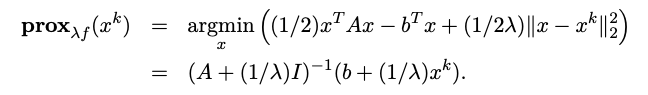

Where $\epsilon = 1/\lambda$
主角 - Proximal Gradient Descent
臨近類方法是用於處理目標函數中含有非光滑項,並且該非光滑項是“臨近友好的”,意思就是它的臨近算子 (proximal operator) 是容易計算的,或是有閉式解。首先考慮一般問題 \(\min_x f(x) + g(x)\)
這裡的 $f(x)$ 是光滑的,而 $g(x)$ 為非光滑的,通常為某種正則函數,或是 (非光滑) L1-norm 之類,當然也有可能為某個約束集 (constraint set) 的指示函數 (indicator),這個時候就變成約束優化 (constrained optimization) 問題了。
PGD 的疊代法:
$x_{k+1} = \arg \min_x {f(x_k) + \nabla f(x_k)(x-x_k) + \frac{1}{2\alpha_k}(x-x_k)^2 + g(x)} = prox_{\alpha_k g}(x_k - \alpha_k \nabla f(x_k)) $
此處 $\alpha_k$ 是基於光滑函數 $f(x)$,可以收斂比較快。
Proximal Gradient Descent 可視爲分為兩步:
Step 1: 在光滑的 $f(x)$ 執行標準的 Gradient Descent: $z_k = x_k - \alpha_k \nabla f(x_k)$
Step 2: 在非光滑 (但 proximal friendly) 的 $g(x)$ 執行 proximal operation: $x_{k+1} = prox_{\alpha_k g} (z_k) = z_k - \alpha_k \nabla M_{\alpha_k g}$
當不可微的凸函數的形式為 $g(\boldsymbol{w})=|\boldsymbol{w}|_1$ 時,則對應的軟閾值函數為
\(\left[\mathcal{S}_t(\boldsymbol{w})\right]_i= \begin{cases}w_i-t, & \text { if } w_i>t \\ 0, & \text { if }\left|w_i\right| \leq t \\ w_i+t, & \text { if } w_i<-t\end{cases}\)
如果 $g$ 是 L1-norm (Lasso) with parameter $\lambda$,
\(\begin{aligned}\boldsymbol{w}^k & =\operatorname{prox}_{\alpha g(\cdot)}\left(\boldsymbol{w}^{k-1}-\alpha \nabla f\left(\boldsymbol{w}^{k-1}\right)\right) \\& =\mathcal{S}_{\alpha}\left(\boldsymbol{w}^{k-1}-\alpha \nabla f\left(\boldsymbol{w}^{k-1}\right)\right)\end{aligned}\)
其中,變數上標的 $k$ 表示當前疊代次數。
Lasso 的 sparsity (係數為 0) 的特性也可以從此看出!!
Lasso 其實也即是 quantization, 只是 apply 在 0 附件 only!
- 假如 $g(x)$ 是 L1-norm, $f(x) + g(x)$ 稱爲 Lasso regularization. Proximal operation of L1 norm 對應一個 backward operation (見下圖紅線). 所以 PGD 有時稱爲 forward (GD, 下圖綠綫)-backward (L1 regularization, 下圖紅線) algorithm.

- 假如 $g(x)$ 是 indicator function (0 in the constraint domain, $\infty$ otherwise) 情況下, proximal operation 可以視爲 projection operation. 如果 GD 把 $z_k$ 移動出 constraint domain, proximal operation 再把 $z_k$ 投影回 constraint domain as $x_{k+1}$ .
PGD Summary
如果 $L(x) = f(x) + g(x)$,$f(x)$ 是光滑函數;$g(x)$ 是非光滑函數但是 proximal operation friendly.
-
如果 $f(x)=0$, 直接用 $x_{k+1} = prox_{\lambda g}(x_k)$
-
標準的 PGD:

-
還有 ADMM

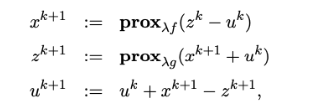
- 特例就是 x - z = or x = z
- Linearized ADMM
- $\min f(x) + g(Ax)$
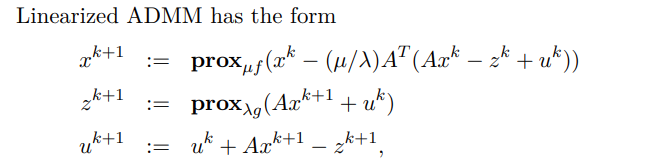
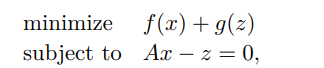
PGD 三種特例
- $g = 0 \to $ PGD = gradient descent (trivail)
- $g = I_C \to$ 如果 $g$ 是 indicator function, PGD = projected gradient descent
- $f = 0 \to$ Proximal minimization algorithm (一般沒有太大用途)
Proximal Minimization Algorithm
$x^* = prox_{\lambda f}(x^) \text{ iff } x^$ is the minimum. \(\begin{aligned}\operatorname{prox}_{\gamma g}(x) & =\arg \min _z\left\{g(z)+\frac{1}{2 \gamma}\|z-x\|_2^2\right\}\end{aligned}\)
假設 $f(x) = 0$
$x_{k+1} = prox_{\lambda g}(x_k)$
最後會收斂到最小值,只要 $g$ 是 contracting function.
Conjugate Function
在引入 conjugate function 後,事情變得更有趣!
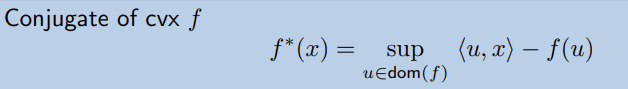
主要用到的就是共軛函數的性質,首先,對於一個正常閉凸函數,可以表示成:
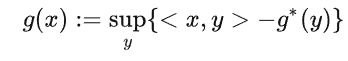
這裡 $g^$ 是一個凸函數,根據 Conjugate Correspondence Theorem,我們知道“強凸函數”的共軛是一個光滑函數。上式中, $g$ 表達成了 $g^$ 的共軛函數,那麼我們是不是可以通過加個二次正則,使得 $g^*$ 加上這個函數變成強凸函數,這樣就起到了光滑的作用了。利用這個定理,我們很容易得到下面這個光滑化函數
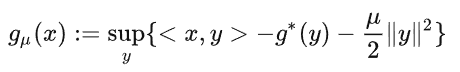
非常重要,可以證明: \(g_u(x) = M_{\mu g}(x)\) [@dengSmoothFramework2020]
$M_{\mu g}(x) = \inf_{z} \left{ g(z) + \frac{1}{2\mu}(x-z)^2\right} = g_{\mu}(x) \le g(x)$
Obviously, 如果 $\mu \to 0\Rightarrow g_{\mu}(x) \to g(x)$
也就是把非光滑的 $g(x)$ 可以轉換成光滑而且強凸函數的 conjugate of 加料 conjugate function $g_{\mu}(x)$; 剛好這個 conjugate of 加料 conjugate function 正好就是 Moreau envelope function!
Moreau Decomposition
可以證明 Moreau Decomposition
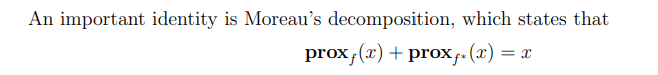
我們直接看例子:$g(x) = \vert x \vert$ 也就是 L1 norm.
L1 norm 對應的 conjugate function 是 indicator function: $g^*(x) = I_C(x)$ 如下.
此處 $C = [-1, 1]$ in $\R^1$ or $C = |x|_{\infty} \le 1$ in $\R^n$
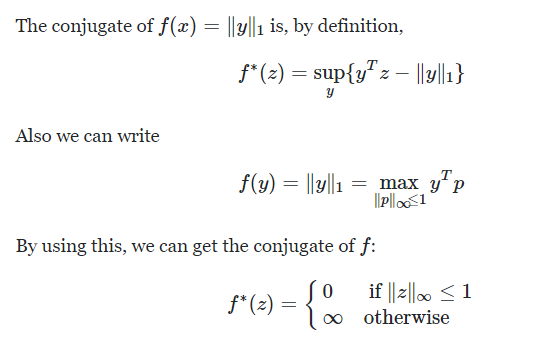
L1 norm $g(x)$ 對應的 proximal function 是 soft-threshold function 如下。 \(prox_g(x)= \begin{cases}x-1, & \text { if } x>1 \\ 0, & \text { if }\left|x\right| \leq 1 \\ x+1, & \text { if } x<-1\end{cases}\)
Indicator function $g^*(x)$ 對應的 proximal function 是 projector to $C$ 如下。 \(prox_{g^*}(x)= \begin{cases}1, & \text { if } x>1 \\ x, & \text { if }\left|x\right| \leq 1 \\ -1, & \text { if } x<-1\end{cases}\)
可以確認:Moreau decomposition: $x = prox_{g}(x) + prox_{g^*} (x)$
Q&A 但因爲 \(\begin{aligned}&\operatorname{prox}_{\gamma g}(x)=x-\gamma \nabla M_{g\gamma}(x)\end{aligned}\) 所以 $\nabla M_g(x) = prox_{g^*}(x)$? YES!
$M_g(x)$ 是 Huber function, 是 $g(x) = \vert x \vert$ 的下界光滑函數。 \(M_{g}(x)=\inf _z\left\{|z|+\frac{1}{2 }(z-x)^2\right\}= \begin{cases}\frac{1}{2} x^2, & |x| \leq 1, \\ |x|-\frac{1}{2}, & |x|>1 .\end{cases}\)
\[\nabla M_{g}(x)=\begin{cases}1, & \text { if } x>1 \\ x, & \text { if }\left|x\right| \leq 1 \\ -1, & \text { if } x<-1\end{cases}\]Performance Comparison
Convergence Rate
一般的 $f(x) + g(x)$ 非光滑函數。以 L1 norm (Lasso) 爲例。
如果用 sub-gradient, $O(1/\epsilon^2)$
如果用 proximal gradient descent, $O(1/\epsilon)$
如果加上 accelerated PGD (or momentum PGD), $O(1/\sqrt{\epsilon})$
Lasso of Quadratic
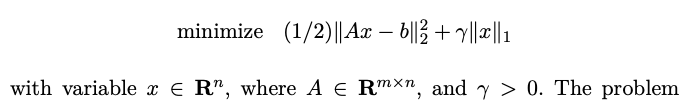
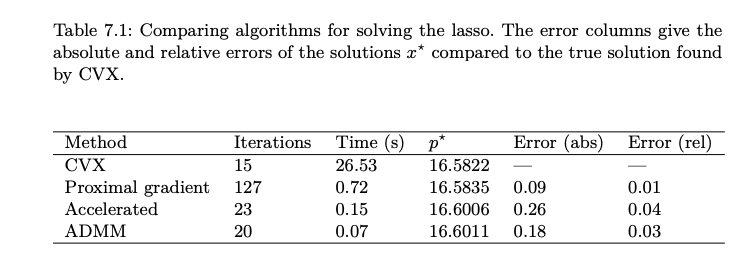
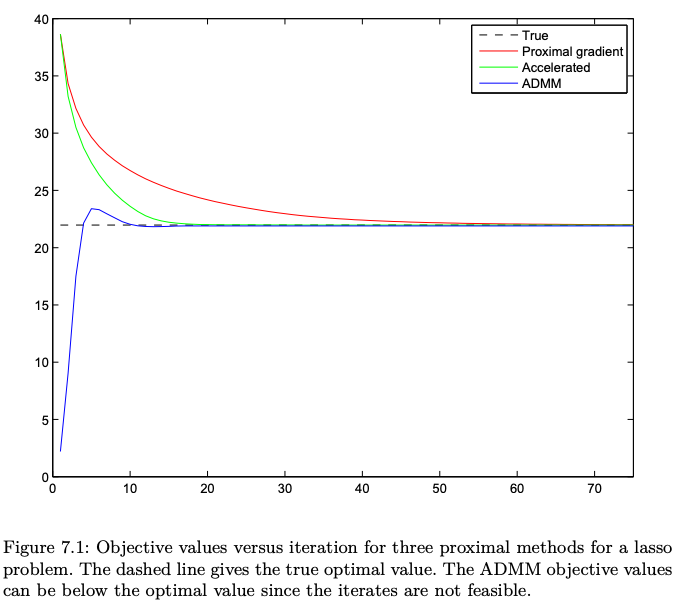
CVX: 2nd order method : fast and accurate but expensive
Proximal gradient: 1st order, slow
Accelerated Proximal: 1st order, fast
ADMM: 1st order, fastest
Appendix A
We can rearrange terms to express $M_{\gamma f}(x)$ in the following form: \(\begin{aligned} & M_{\gamma f}(x)=\frac{1}{2 \gamma}\|x\|^2-\frac{1}{\gamma} \sup _y\left\{x^T y-\gamma f(y)-\frac{1}{2}\|y\|^2\right\} \\ &=\frac{1}{2 \gamma}\|x\|^2-\frac{1}{\gamma}\left(\gamma f+\frac{1}{2}\|\cdot\|^2\right)^*(x) \\ & \therefore \nabla M_{\gamma f}(x)=\frac{x}{\gamma}-\frac{1}{\gamma} \underset{y}{\operatorname{argmax}}\left\{x^T y-\gamma f(y)-\frac{1}{2}\|y\|^2\right\} \\ &=\frac{1}{\gamma}\left(x-\operatorname{prox}_{\gamma f}(x)\right) \\ & \Rightarrow \operatorname{prox}_{\gamma f}(x)=x-\gamma \nabla M_{\gamma f}(x) \\ & \operatorname{prox}_{\gamma f}(x)=x-\gamma \partial M_{\gamma f}(x), \\ & M_{\gamma f}(x)= \min _y\left\{f(y)+\frac{1}{2 \gamma}\|x-y\|^2\right\} \\ &= \min _y\left\{f(y)+\frac{1}{2 \gamma}\|z\|^2\right\} \text { such that } x-y=z \end{aligned}\) (Note the substitution trick here is a very useful technique.) The Lagrangian and the Lagrange dual function are given by \(\begin{aligned} \mathcal{L}(y, z, \lambda) & =f(y)+\frac{1}{2 \gamma}\|z\|^2+\lambda^T(x-y-z) \\ & =\left[f(y)-\lambda^T y\right]+\left[\frac{1}{2 \gamma}\|z\|^2-\lambda^T z\right]+\lambda^T x \\ g(\lambda) & =\inf _{y, z} \mathcal{L}(y, z, \lambda) \\ & =\inf _y\left\{f(y)-\lambda^T y\right\}-\frac{\gamma}{2}\|\lambda\|^2+\lambda^T x \\ & =-f^*(\lambda)-\frac{\gamma}{2}\|\lambda\|^2+\lambda^T x \\ f_\gamma(x)=\sup _\lambda g(\lambda) & =\sup _\lambda\left\{-f^*(\lambda)-\frac{\gamma}{2}\|\lambda\|^2+\lambda^T x\right\} \\ & =\left(f^*+\frac{\gamma}{2}\|\cdot\|^2\right)^*(x) \end{aligned}\)
Appendix B : 光滑算法框架
這裡主要用到的就是共軛函數的性質,首先,對於一個正常閉凸函數,可以表示成:
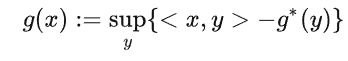
這裡 $g^$ 是一個凸函數,根據 Conjugate Correspondence Theorem,我們知道“強凸函數”的共軛是一個光滑函數。上式中, $g$ 表達成了 $g^$ 的共軛函數,那麼我們是不是可以通過加個二次正則,使得 $g^*$ 加上這個函數變成強凸函數,這樣就起到了光滑的作用了。利用這個定理,我們很容易得到下面這個光滑化函數
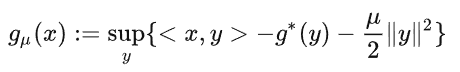
非常重要,可以證明: \(g_u(x) = M_{\mu g}(x)\) [@dengSmoothFramework2020]
也就是光滑函數可以是 Moreau envelope function 或是 conjugate function with L2 norm!
知道了原理,只要後面是個強凸項就可以了,所以可以得到更一般的形式:
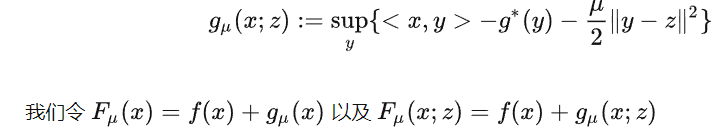
框架一
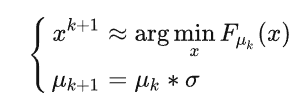
大概思想就是,最開始光滑參數 $\mu_k$ 比較大,也就是很光滑。後面 $\mu_k$ 慢慢減小趨于零。每次我們近似求解光滑化問題,比如:
- 滿足一定的精度,比如 $| \nabla F_{u_k}(x^{k+1})| \le \epsilon_k$
- 執行固定的梯度疊代就跳出
- 只執行一次梯度疊代,即 $x^{k+1} = x^k - \alpha_k \nabla F_{u_k}(x_k)$
- 求到精確解。
這和 sub-gradient 好像一樣?
既然是框架,就要做的general一點,我們考慮(4)式中的光滑化函數
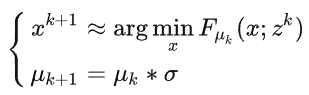
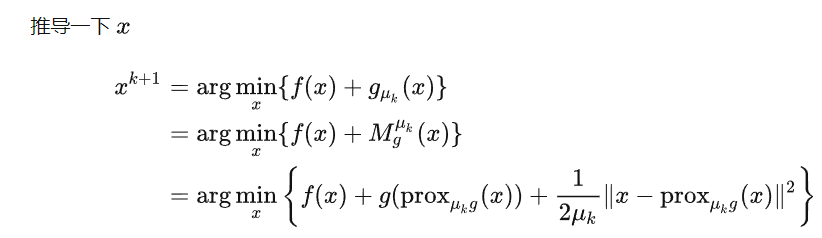
例子一: g(x) 是 indicator function. Prox_g 就是 projection function. Pc(x)
所以 g( prox(x)) = 0!!! 因爲 g(x) 是 indicator, 而且 prox(x) project x 回到 g 的 domain. 所以 g(prox())


Appendix C: PGD 證明
對於優化問題 $\min _{\boldsymbol{w}} f(\boldsymbol{w})+g(\boldsymbol{w})$ ,$f$ 是 smooth, $g$ 是 non-smooth 變數 $\boldsymbol{w}$ 的疊代遞推公式為 \(\begin{aligned} \boldsymbol{w}^k & =\operatorname{prox}_{\alpha g(\cdot)}\left(\boldsymbol{w}^{k-1}-\alpha \nabla f\left(\boldsymbol{w}^{k-1}\right)\right) \\ \end{aligned}\)
疊代遞推公式證明過程
\[\begin{aligned} \boldsymbol{w}^k & =\operatorname{prox}_{\alpha g(\cdot)}\left(\boldsymbol{w}^{k-1}-\alpha \nabla f\left(\boldsymbol{w}^{k-1}\right)\right) \\ & =\arg \min _z g(\boldsymbol{z})+\frac{1}{2 \alpha}\left\|\boldsymbol{z}-\left(\boldsymbol{w}^{k-1}-\alpha \nabla f\left(\boldsymbol{w}^{k-1}\right)\right)\right\|_2^2 \\ & =\arg \min _{\boldsymbol{z}} g(\boldsymbol{z})+\frac{\alpha}{2}\left\|\nabla f\left(\boldsymbol{w}^{k-1}\right)\right\|_2^2+\nabla f\left(\boldsymbol{w}^{k-1}\right)^{\top}\left(\boldsymbol{z}-\boldsymbol{w}^{k-1}\right)+\frac{1}{2 \alpha}\left\|\boldsymbol{z}-\boldsymbol{w}^{k-1}\right\|_2^2 \\ & =\arg \min _{\boldsymbol{z}} g(\boldsymbol{z})+f\left(\boldsymbol{w}^{k-1}\right)+\nabla f\left(\boldsymbol{w}^{k-1}\right)^{\top}\left(\boldsymbol{z}-\boldsymbol{w}^{k-1}\right)+\frac{1}{2 \alpha}\left\|\boldsymbol{z}-\boldsymbol{w}^{k-1}\right\|_2^2 \\ & \approx \arg \min _{\boldsymbol{z}} f(\boldsymbol{z})+g(\boldsymbol{z}) \end{aligned}\]注意: 由於公式第三行中的 $\frac{\alpha}{2}\left|\nabla f\left(\boldsymbol{w}^{k-1}\right)\right|_2^2$ 和第四行中的 $f\left(\boldsymbol{w}^{k-1}\right)$ 均與決策變數 $\boldsymbol{z}$ 無關,因 此公式第三行等於公式第四行。
Reference
[@boydProximalAlgorithms2013]
Math Optimization - PPO
Source
Introduction
在 optimization 最挑戰的問題之一是不可微分性。
我們在 convex optimization 不可微分點使用 sub-differential 就看到不同的算法處理不可微分點。
例如 sub-gradient method, 或是 proximal operator.
不過 convex optimization 只是少數幾個點。在 reinforcement learning 遇到的情況是 discrete sequence decision 所造成的結果。Discrete sequence decision 是 discrete 而不可微分?
解法就是引入概率。這和 gradient descent (GD) 變成 stochastic gradient descent (SGD) 基本一樣?
因爲概率分佈是連續可微分。Discrete sequence decision (policy) 可以視爲一個 sample.
PPO (Proximal Policy Optimization) for Reinforcement Learning
我們先 review policy.
Policy Gradient
用玩 game 做例子。


Appendix
Optimization - Gradient Descent
Source
-
非線性優化方法的總結: https://zhuanlan.zhihu.com/p/85423364?utm_id=0 很好的總結文章
-
Why Momentum Really Works? [@gohWhyMomentum2017]
-
MIT: overview of gradient descent: [@ruderOverviewGradient2016]
Introduction
本文討論 (convex) optimization 方法 $\min_x L(x)$, $x \in \R^n$
$L(x)$ 可以想成是一個 loss function. 我們的目的是找到 $n$ 維的 $x$, 一般稱爲 weight 極小化 loss function.
很多時候 $L(x)$ 是一個複雜的 function, 找到 $x_{min}$ 比 $L(x_{min})$ 更重要,而且只有近似的迭代法。
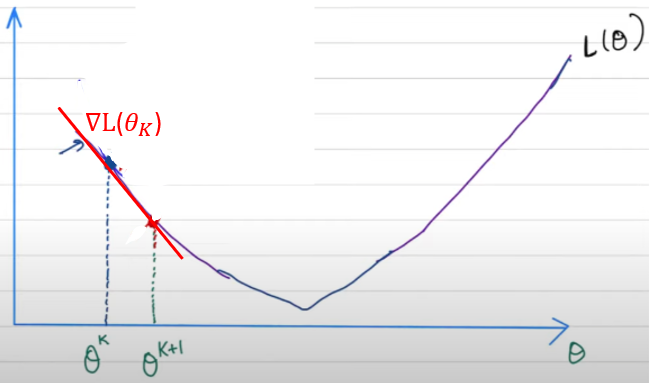
從 deterministic 到 stochastics,從一階到二階,從原始到對偶。光滑到非光滑。
迭代算法就是不斷逼近,化繁為簡,將一個個難問題分為若干個易問題的過程。
化繁為簡包含兩個角度
- 時間: 逐步逼近
- 空間: separable
Deterministic Method
先看最常用而且簡單的方法,就是梯度法 (Gradient Descent).
一階方法:Gradient Descent
Gradient Descent (GD) 方法如下:
\(x_{k+1} = x_k - \alpha \nabla L(x_k)\)
GD 的重點
-
$x$ ,$\nabla L(x) \in \R^n$ 是向量。
-
$\alpha$ 是一個固定的純量。但是每次的 step: $\alpha \nabla L(x_k)$ 是 self-adjusted step.
GD 幾何意義
我們回過來看 gradient descent (GD) 的幾何意義。
-
$L(x)$ 是 convex function
-
$L(x) \ge L(x_k) + \nabla L(x_k) (x-x_k)$ 這可以視爲 Taylor expansion approximation. 因爲 $L(x)$ 是 convex function, 所以大於等於 1st order Taylor expansion. 就是 $L(x)$ 的切綫下界 (lower bound).
-
一般 GD : $x_{k+1} = x_k - \alpha \nabla L(x_k)$. 其中 $\alpha$ 稱爲 learning rate, 似乎只是隨意選擇的 parameter?
-
NO! 其實 $\alpha$ 有清楚的物理意義。就是 $L(x)$的一個 (potential 上界) 抛物綫。
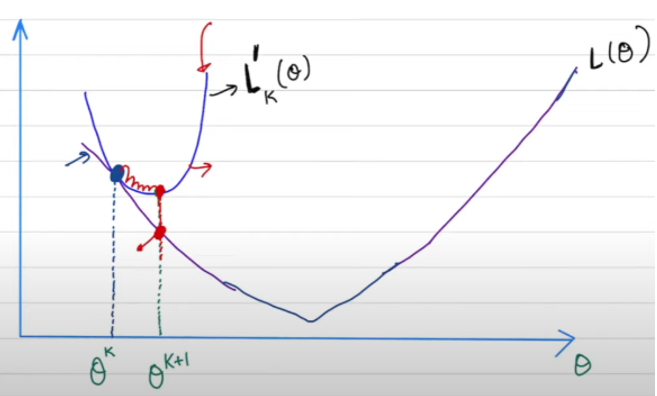
- $f(x) \ge L(x) \ge L(x_k) + \nabla L(x_k) (x-x_k)$. 此處 $f(x)$ 是一個二次抛物綫,滿足
- $f(x_k) = L(x_k)$
- $\nabla f(x_k) = \nabla L(x_k)$
- $\nabla f(x_{k+1}) = 0$
-
如何解 $f(x)$: $f(x)= a x^2+b x+ c = L(x_k) + \nabla L(x_k)(x-x_k) + k(x-x_k)^2 $ 滿足 1 and 2.
-
代入 3. $\nabla L(x_k) + 2 k (x_{k+1} - x_k) = 0$, 也就是
-
$x_{k+1} = x_k - \frac{1}{2k} \nabla L(x_k) $. 比較 GD $x_{k+1} = x_k - \alpha \nabla L(x_k)$ 可以得到 $k = \frac{1}{2\alpha}$
-
$f(x)= L(x_k) + \nabla L(x_k)(x-x_k) + \frac{1}{2\alpha}(x-x_k)^2 $!!
-
上式看起來是 Taylor expansion of 2nd order,不過其實不是。而 (預期) 是上界。
-
-
$L(x_k) + \nabla L(x_k)(x-x_k) + \frac{1}{2\alpha}(x-x_k)^2 \ge L(x) \ge L(x_k) + \nabla L(x_k) (x-x_k)$.
- 如果 $\alpha$ 接近 0,上面的平方項一定可以滿足上界的要求!但是 GD 的 step 就非常小。
- 如果 $\alpha$ 很大,大過某個 threshold,上面的平方項有可能變成下界而非上界!所以 GD 一個重要的任務就是要選擇 $\alpha$ 盡量大但是不能超過某個 threshold. 幾何上對應的就是比較緊的上界。
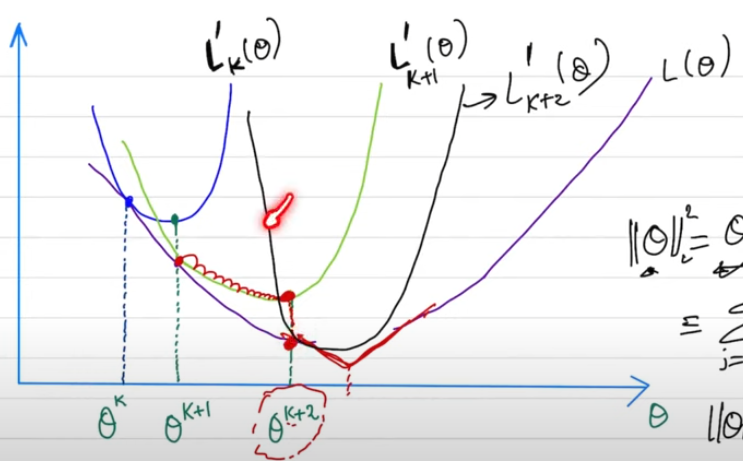
定義域看 GD
根據以上幾何的詮釋,可以得到以下的迭代表示法:
$x_{k+1} = x_k - \alpha_k \nabla L(x_k) = \arg \min_x {L(x_k) + \nabla L(x_k)(x-x_k) + \frac{1}{2\alpha_k}(x-x_k)^2 } $
一般的 GD: $\alpha_k$ 會選擇一個常數,小於某個 threshold ~ $L(x_k)$ 曲率的倒數 (Hessian 的倒數)。如果 $L(x_k)$ 附近越接近直綫,$\alpha_k$ 可以越大,就是越 aggressive step.
$\alpha_k$ 也可以變成 optimization 的目標,比如最速下降法这样选择步长 \(\alpha^k=\arg \min _\alpha L\left(x^k-\alpha \nabla L\left(x^k\right)\right)\) 或者采用线搜索的形式找到一个满足线搜索的步长即可。更快速的步长为一种叫BB方法的步长 \(\alpha^k=\frac{\left(s^k\right)^T s^k}{\left(s^k\right)^T y^k},\) 其中 $s^k=x^k-x^{k-1}, y^k=\nabla L\left(x^k\right)-\nabla L\left(x^{k-1}\right)$ 。
这个步长其实是对Hessian矩阵倒數的一个近似,可以叫它伪二阶方法。BB步长及其有效,对于某些方法的提速有奇效,你可以在各种新的方法中看到它的身影。可惜不是单调的,对于一般非线性函数没有收敛性保障,所以通常会结合线搜索使用。
GD 收斂問題
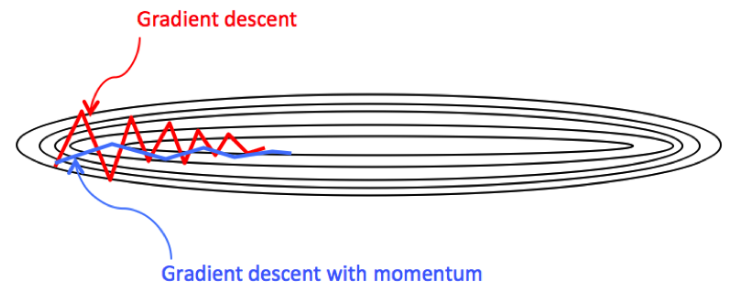
GD 最大的問題是多維空間 (即使 2D) 無法快速收斂! 原因是多維空間只要有一維的曲率很大,如果 $\alpha$ 大於這個方向的曲率倒數,就會造成振盪非常久才收斂,甚至不收斂。
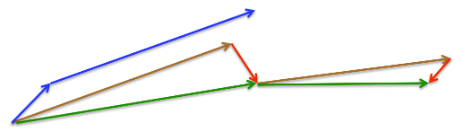
此時就要说一下共轭梯度方法,这个方法可以这样理解: 它觉得负梯度方向不好,所以去改良它,用上一步方向对它做一个矫正。共轭梯度方法其实动量方法还有heavy ball方法非常相似 \(\begin{aligned} & x^{k+1}=x^k+\alpha^k p^k \\ & p^{k+1}=-\nabla L\left(x^{k+1}\right)+\beta^k p^k \end{aligned}\)
比較 GD 和 momentum GD 方法的差異。我們用 2D 的等高圖來看。
[@gohWhyMomentum2017]
二階方法:牛頓法
基本使用二階 Taylor expansion, 使用真的 Hessian 而非用上界抛物綫迭代近似。
首先对原函数做二阶泰勒展开,那么将得到二阶算法 \(\begin{aligned} x^{k+1} & =\arg \min \left\{L\left(x^k\right)+<\nabla L\left(x^k\right), x-x^k>+\frac{1}{2}\left(x-x^k\right)^T \nabla^2 L\left(x^k\right)\left(x-x^k\right)\right\} \\ & =x^k-\left(\nabla^2 L\left(x^k\right)\right)^{-1} \nabla L\left(x^k\right) \end{aligned}\) 这就是牛顿方法。
- 和 GD 比較,牛頓法就是把 $\alpha_k$ 變成 Hessian 的倒數
- 当维数太大时,求解Hessian矩阵的逆很费时间,所以我们就去用向量逼近,这 样就得到了拟牛顿方法, 这里就不讲了。
- 有时候我们希望能够控制每一步走的幅度,根据泰勒展开的逼近程度来决定我们这一步要圭多远, 这样就得到了信赖域方法
\(\begin{aligned} & x^{k+1}=\arg \min \left\{L\left(x^k\right)+<\nabla L\left(x^k\right), x-x^k>+\frac{1}{2}\left(x-x^k\right)^T \nabla^2 L\left(x^k\right)\left(x-x^k\right)\right\} \\ & \text { s.t. } x-x^k \in \Delta^k \end{aligned}\) 这里的 $\Delta^k$ 为信赖域半径,如果泰勒展开逼近的好,我们就扩大半径,否则就缩小半径。 还有个类似于信赖域方法的叫cubic正则方法 \(\begin{aligned} x^{k+1}=\arg \min \left\{L\left(x^k\right)+<\nabla L\left(x^k\right), x-x^k\right. & >+\frac{1}{2}\left(x-x^k\right)^T \nabla^2 L\left(x^k\right)\left(x-x^k\right)+\frac{1}{\alpha^k} \| x \\ & \left.-x^k \|^3\right\} \end{aligned}\) 这个cubic正则项和信赖域有着差不多的功效。
Stochastic Method
我們把原來的問題重新 formulate to fit 常見的機器學習優化問題。
原始的問題: $\min_x L(x)$, $x \in \R^n$
在機器學習中,我們有 N 個 labeled data. Loss function 改成 $L(x) = \frac{1}{N}\Sigma_{i=1}^N f_i(x)$
$f_i(x)$ 可以是 regression loss function (L2 norm or logistic regression function), classification function (entropy function)。基本都是凸函數。
$\min_x L(x) = \min \frac{1}{N} \sum^N_{i=1} f_i(x) = \min_x \sum^N_{i=1} f_i(x)$, $x \in \R^n$
此處的 $N$ 是機器學習的 samples; $x$ 是 weights, $n$ 是 number of weight.
一般 N 非常大,可以是幾百萬。同時 $N \gg n$.
如果使用 GD, 每一次迭代,最低的代价也要算一次梯度。如果 N 很大的时候,算一次完整的函数梯度都费劲,这时候就可以考虑算部分函数梯度。如果這些 sample 都是 independent, 部分函數的梯度法也會收斂到完整函數的梯度法。
一階方法:Stochastic Gradient Descent (SGD)
\[\begin{aligned}x^{k+1} & =\arg \min \left\{f_{i_k}\left(x^k\right)+<\nabla f_{i_k}\left(x^k\right), x-x^k>+\frac{1}{2\alpha^k} \|x-x^k\|^2\right\} \\& =x^k-\alpha^k \nabla f_{i_k}\left(x^k\right)\end{aligned}\]此處 $i_k \in 1, \cdots, N$
一個更常用的變形是 mini-batch, 也就是用多個 samples, 通常是 4/8/16/32/…/256, 計算 gradient.
其他一系列的 stochastic GD 變形
[@gohWhyMomentum2017]
Adam, Adadelta, Adagrad, RMSProp
Netsterov, AdamW
二階方法:sub-sample Newton Method
一阶方法的缺陷就是精度不够高,所以有时候还是需要用到二阶方法,但是呢,我们又嫌二阶方法太慢,所以干脆就对Hessian矩阵也采样,这样就得到了subsample Newton方法 \(\begin{aligned}x^{k+1} & =\arg \min \left\{f_{i_k}\left(x^k\right)+<\nabla f_{i_k}\left(x^k\right), x-x^k>+\frac{1}{2}\left(x-x^k\right)^T \nabla^2 f_{i_k}\left(x^k\right)\left(x-x^k\right)\right\} \\& =x^k-\left(\nabla^2 f_{i_k}\left(x^k\right)\right)^{-1} \nabla f_{i_k}\left(x^k\right)\end{aligned}\)
其他一系列的二階 stochastic GD 變形
Google: Lion, Tiger
Stanford: Sophia
Reference
Math AI - Optimization II
Source
YouTube
Background
Stochastic gradient descent
- Noisy Gradient
- Stochastic Optimization
- Random coordinate descent!
Noisy gradients
Instead of $\nabla f $, 我們得到的是 $E[g] = \nabla f$
Stochastic Optimization
問題描述
$\min: f(x)$, st: $x \in C$ 改成
$\min_x: E_\xi [f(x); \xi]$, st: $x \in C$
什麽是 $\xi$, 就是 machine learning 的 training parameter.
例如在 linear regression $\min_x E[(y - \xi^T x)^2]$
$(y_1, \xi_1), (y_2, \xi_2), …$ 就是 training data.
Empirical Risk Minimization Z(ERM) = $\min f(x) = \frac{1}{n} \sum f_i(x)$
在 classification 問題:
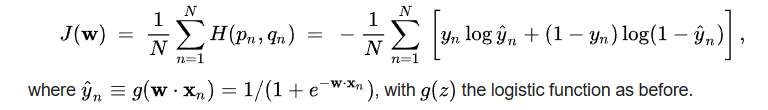
NO, 應該反過來。$x$ 最後是 training parameter 可以使用 gradient descent 得到。 $\xi$ 則是 data with distribution.
Full GD is very expensive! going over all data points.
SGD
GD 有 self-tuning 特性
sub-GD 沒有 self-tuning 特性
在 SGD 也是一樣?yes
Sub-gradient proportional to 1/sqrt(T)
Gradient descent proportional to 1/T
SGD 1/sqrt(T)

SGD is similar to sub-differential!!
No self-tuning for SGD